一种基于RANSAC算法的无人机图像校正方法

梁 强

(广东工业大学土木与交通工程学院 广东 广州 510006)

一、数字图像相关性

数字图像相关测量方法(DIC)[1][2]的基本原理是通过追踪物体表面的散斑图像，实现变形过程中物体表面三维位移的测量。在相关算法运行之前，各取大小为m×m的子区域，这个子区域中心为所感兴趣的像素点。在图像移动的过程中，定义相关系数C(f,g)，通过改变△x和△y的值，即在变形后图像上移动子区域，可以得到不同的C(f,g)值。使得C(f,g)取得最大值对应的△x和△y即是子区域中心点P(x,y)的位移，该公式求得的是物体表面的整像素位移值。目标点变形前后坐标关系如下：

x′=x+△x
y′=y+△y

(1)

要得到变形前后图像待测点的位移矢量，就要找到与变形后图像中与参考子区最相似的目标子区。引入相关函数C(f,g)用于评价变形前后图像子区相似程度。通过改变△x和△y的值在变形后图像上搜索与参考子区相关函数C(f,g)为极大值的子区即为待求的目标子区。本文选用计算变形前后图像子区相关系数的公式如下：

(2)

式中,f,g分别为参考子区和变形子区图像像素的灰度分布值；A为子区的面积；相关值C的大小随△x,△y而变化，0≤C≤1；当相关函数取得极大值时，输出的结果(△x,△y)就是待测点变形的像素位移矢量。

二、单应性变换

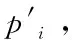
(3)

像素点用齐次坐标表示，展开式得到对应一组参考点的单应性变换关系如下：

(4)

式在比例因子s≠0下成立。等式中由于使用了齐次坐标，单应性矩阵可以利用h33归一化，得新的单应性矩阵，其中h33=1。那么单应性矩阵就变成了仅有8个自由度的矩阵。由式得到第i组对应参考点之间的映射方程如下：

(5)

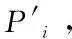
(6)

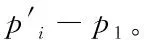
三、RANSAC算法

RANSAC算法的基本思路为：首先选择出可以估计出模型的最小数据集(对于直线拟合来说就是两个点，对于计算Homography矩阵就是4个点)，之后使用这个数据集来计算出数据模型；接下来将所有数据带入这个模型，计算出代价函数；第四步，比较当前计算代价函数和之前代价函数的大小，记录较小代价函数对应的模型参数；最后一步，重复1-4步，直到迭代结束或者当前模型已经足够好了(代价函数小于预先设定阈值)。[4][5]

代价函数f(x)通常取：

(7)

迭代次数k通常由下式进行确定：

(8)

其中P为置信度，通常取0.995。“内点”的概率t是一个先验值，通常使用自适应迭代次数的方法计算。即开始设定一个无穷大的迭代次数，然后用当前“内点”数量和预计结果的比值作为t来估计出迭代次数。

四、实验结论

将RANSAC算法运用在单应性变换方法进行图像校正，利用VS2015和Opencv自编程相应程序进行数据处理论证两种方法的准确性。得出控制点变换以及改进方法的实验结果如图2所示。

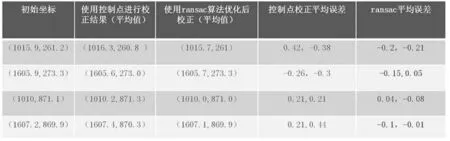
图1 两种方法的比较以及误差分析

由图1可知，RANSAC算法的图像校正比控制点变换的平均误差更加小，在4组实验当中该方法显得更加精确稳定。其值接近于初始坐标。