基于四元数理论的2UPS-PU并联机构位置反解

曹建平，孙文柱,王海东，任 剑

(海军航空大学,山东 青岛 266041)

0 引言

并联机构位置反解是进行并联机构运动学分析的第一步。所谓位置反解是已知末端动平台的位置和姿态反过来求取驱动元件的参数的过程。目前关于并联机构位置反解的研究主要有矢量法[1]、旋转换矩阵[2]和旋量[3]等方法。这些方法都可以归结为基于几何的矢量分析，当机构结构复杂时求解繁琐且容易出错。

本文将四元数理论引入到并联机构位置反解分析中，利用纯四元数表示矢量位置，单位四元数表示矢量的旋转和方位，从而将并联机构位置反解的问题转化为代数推导，以2UPS-PU并联机构为例阐述了计算过程，并结合MATLAB和SolidWorks仿真来验证仿真算例。

1 四元数及其在刚体方位描述的应用

四元数[4]是复数的推广，最早由爱尔兰数学家哈密尔顿提出。设i、j、k符号满足下列乘法关系：

i2=j2=k2=-1

(1)

ijk=-1

(2)

则四元数q可定义为

q=a+bi+cj+dk

(3)

其中a、b、c、d为实数，q的共轭四元数为

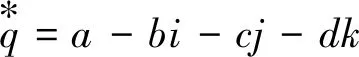
(4)

当a=0时称为纯四元数，此时满足：

q=bi+cj+dk

(5)

可知纯四元数与R3空间点一一对应，同时与三维矢量一一对应，因而可用纯四元数来表示矢量的加、减、点乘、叉乘等运算。

当四元数各参数满足：

a2+b2+c2+d2=1

(6)

此时四元数q称为单位四元数，也可以表示为

q=cosθ+sinθ(cosαi+cosβj+cosγk)

(7)

R3空间矢量的旋转可以利用单位四元数q表示。设矢量v1=(x1,y1,z1)′和v2=(x2,y2,z2)′，v2是v1旋转得到的。在三维空间内描述矢量旋转需要给出旋转轴的方位和旋转的角度，如图1所示。

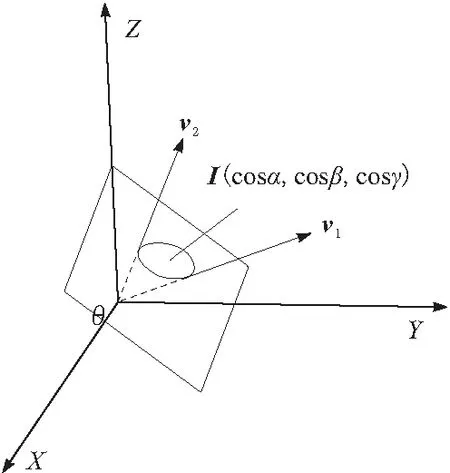
图1 矢量绕轴旋转

其几何意义是：v1绕轴I旋转θ得到v2，那么已知旋转轴I的方向余弦I=(cosα,cosβ,cosγ)和旋转的角度θ即求得v2。这个过程可用四元数进行运算得到，首先利用纯四元数表示2个矢量：

qv1=x1i+y1j+z1k

(8)

qv2=x2i+y2j+z2k

(9)

则可得[4]

(10)

其中qR为单位四元数，可表示为

(11)

将qR称为对应旋转操作的旋转四元数。

2 机构描述

基于以上分析，纯四元数与单位四元数组合可用于建立并联机构的运动方程，从而避免了繁琐复杂的几何推导，以图2所示的2UPS-UP并联机构为例说明。2UPS-UP并联机构是一种两转一移三自由度并联机器人常采用的构型，在Tricept机器人[5]、四足步行机器人[6]和三自由度并联摇摆台[7]等领域应用广泛。该并联机构包括动平台B1B2B3和静平台A1A2A3，动平台B1B2B3通过2个结构完全相同的无约束UPS支链和1个恰约束PU支链相连，3个支链中的移动副作为主动件。该并联机构存在以下几何关系：3条支链AiBi(i=1,2,3)与动平台B1B2B3和固定平台A1A2A3的连接点Bi(i=1,2,3)、Ai(i=1,2,3)呈等腰直角三角形分布，其中B1B2B3的直角边边长为e，A1A2A3的直角边边长为f；PU支链一端通过万向铰B3与动平台B1B2B3相连接，另一端与固定平台A1A2A3固定连接，PU支链与其在静平台上的投影的夹角为φ，而投影与固定平台A1A2A3直角边夹角为45°。设3条支链的长度分别为l1、l2和l3，并分别在静平台和动平台上建立A1-XYZ和B1-UVW直角坐标系。

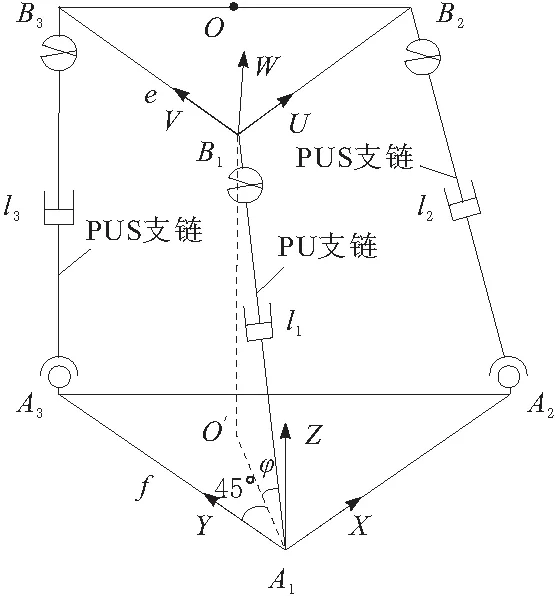
图2 2UPS-UP并联机构简图

3 基于四元数的机构位置求解

设A1-XYZ的3个正交基矢量集为Γ1={u1,v1,w1}，利用纯四元数分别表示为

(12)

则在Γ1下，静平台的3个连接点A1、A2和A3可用纯四元数表示为

(13)

动平台相对于静平台具有2个转动自由度，首先以X轴为转动轴逆时针旋转α，则对应旋转四元数为

(14)

在qR1作用下，正交基矢量集Γ1转换为Γ2={u2,v2,w2}，将式(14)代入式(10)中，Γ2可用四元数分别表示为

(15)

接着以Y轴为转动轴逆时针旋转β，则对应的旋转四元数为

(16)

在qR2作用下，正交基矢量集Γ2转换为Γ3={u3,v3,w3}，将式(16)代入式(10)中，利用四元数分别表示为

(17)

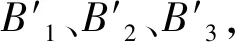
(18)

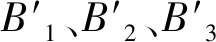
(19)

则动平台的3个连接点B1、B2、B3可用四元数表示为

(20)

则支链L1、L2和L3可用四元数表示为

(21)

将式(13)、式(18)、式(19)和式(20)代入式(21)，可得

基于以上推导可完成2UPS-PU并联机构的运动位置反解，即已知执行平台的位置和方位计算动力元件参数。在2UPS-PU并联机构中，动平台有3个自由度，以动平台B1为基准点，设其距静平台垂直高度为h，用上文提到的α和β表征动平台的方位，则2UPS-PU并联机构3条动力支链的长度l1、l2和l3可表示为

(23)

将式(22)代入式(23)后可得

(24)

式(24)即为2UPS-PU并联机构的反解方程。

4 仿真算例验证

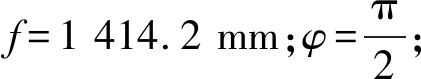
(25)

将h、α和β分别代入式(24)中，利用MATLAB仿真，设置步长为0.1，可得到l1、l2和l3的变化规律如图3所示。

利用SolidWorks建模，给出2UPS-PU并联机构的CAD三维模型，并利用Motion插件进行运动仿真，如图4所示。将反解得出的l1、l2和l3分别作为图4所示直线马达1、直线马达2和直线马达3的运动输入参数，仿真时间为32 s，并设置动平台的中心记录其运动路径并保存为计算结果。

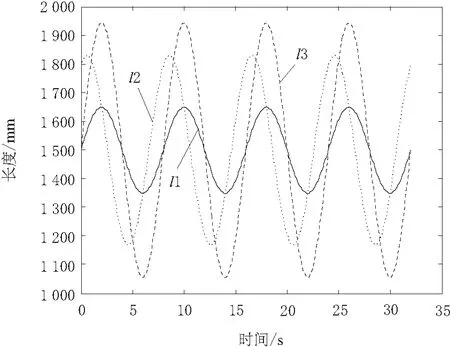
图3 并联机构算例的位置反解结果

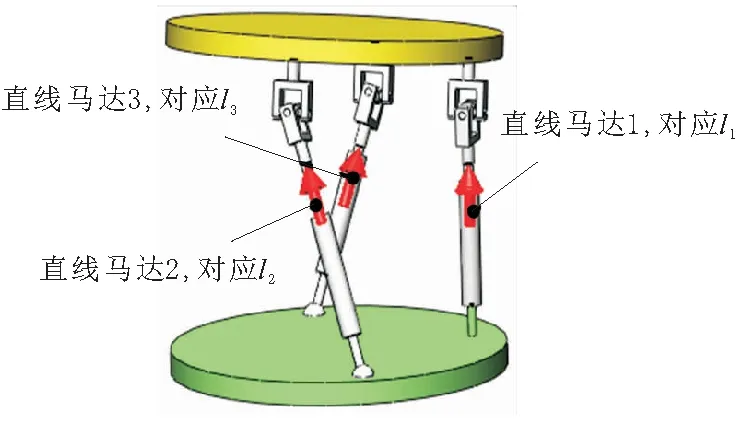
图4 并联机构的CAD三维模型及驱动

图5给出了并联机构在第1秒、第3秒、第6秒和第10秒的仿真运动可视化结果，10 s后动平台进行周期性运动。图5d给出了第10秒中心点的完整运动轨迹图。

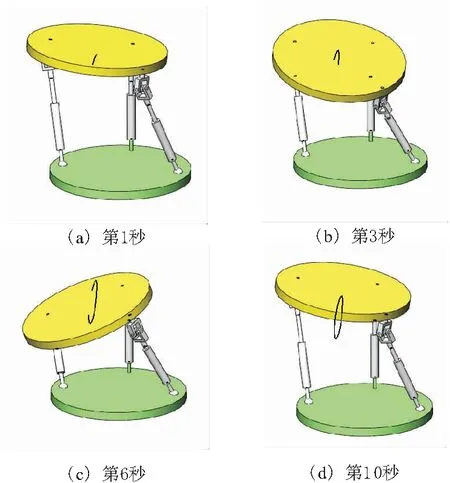
图5 SolidWorks软件的仿真可视化结果

将图5所示的中心运动轨迹的数值结果从SolidWorks中取出，为进行对比每隔5个数进行平均筛选，并在MATLAB中绘出，得到的仿真轨迹结果如图6所示。

分析如图2所示的动平台中心点的理论运动轨迹，动平台中心点O位于动平台B1B2B3的斜边中点上，则其位置可用纯四元数表达为

(26)

代入式(17)～式(20)后，可得

(27)

在坐标系Γ1下，可表示为

(28)

将式(25)及相关的结构参数代入到式(28)中，设置步长为0.1，可得到中心点O的理论轨迹如图6实线所示的理论轨迹结果。

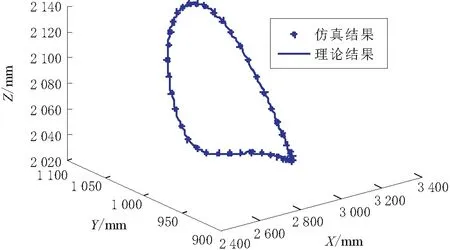
图6 动平台中心的理论轨迹与仿真轨迹对比

由图6可知，该方法的理论结果与仿真结果一致，从而说明了基于四元数理论的2UPS-PU并联机构的位置反解方法的正确性和有效性。

5 结束语

将四元数理论用于2UPS-PU并联机构位置反解，从应用过程得出以下结论：

a.利用四元数理论推导得出2UPS-PU并联机构位置反解方程，相对于传统几何方法，该方法直观易于理解。

b.利用MATLAB和SolidWorks Motion验证了结果的正确性。

c.该方法具有一般性，可推广至其他任意并联机构。