马尔科夫链蒙特卡洛地面磁共振信号参数提取
郜泽霖, 魏 晋, 蒋川东, 刁 庶
(吉林大学 仪器科学与电气工程学院, 长春 130061)
0 引 言
地面磁共振技术(MRS: Magnetic Resonance Sounding)以其无损、 定量、 直接等优势, 广泛应用于地下水探测和水文地质调查等领域[1]。在测量过程中, 获得的MRS信号十分微弱, 易受到各种环境噪声的干扰, 低信噪比是MRS信号提取面临的最大挑战。
环境噪声主要分为尖峰噪声、 工频谐波噪声和随机噪声。尖峰噪声是由天空中打雷放电、 开关突然的开闭等引起的瞬时大幅度干扰, 会对MRS信号的后续滤波叠加处理造成非常严重的影响, 一般是首先去除的一类噪声。目前, 比较成熟的去噪方法有能量运算方法[2]、 尖峰建模方法[3]、 统计叠加方法和小波模极大值方法[4]。工频谐波噪声是由高压输电线、 变压器和其他电器设备产生的, 在测量数据中最常出现, 影响最大。由于工频谐波噪声在多通道采集时具有较强的相关性, 因此可以采用自适应噪声抵消[5]等方法进行消除。随机噪声是一种没有规律, 但统计规律服从高斯分布的噪声, 分为加性随机噪声与乘性随机噪声两类。对加性噪声有基于L1范数的低场核磁共振T2谱稀疏反演方法[6]、 稀疏表示法[7]、 时频峰值滤波法[8]等方法降低对MRS信号的干扰, 但对乘性随机噪声还没有成熟的处理算法。
笔者针对仪器采集数据中的加性和乘性随机噪声, 使用马尔科夫链蒙特卡洛(MCMC: Markov Chain Monte Carlo)算法[9-14]提取MRS复包络信号的参数。常规的非线性拟合方法不适用于乘性随机噪声, 而传统的蒙特卡洛算法的计算量大, 笔者将MCMC方法运用于MRS信号提取, 不仅可以获得最优的算法性能, 而且其计算复杂度也不会随着样本次数的增加而明显增加, 仅与迭代次数成线性关系。
1 磁共振数据信噪特征
根据文献[1], 通过对采集到的MRS数据进行去噪处理, 消除数据中的尖峰噪声和工频谐波噪声, 再经过希尔伯特变换和低通滤波处理后, 可获得MRS信号的复包络表达式
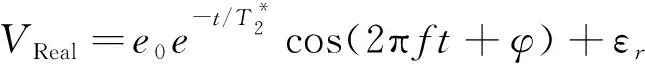
(1)
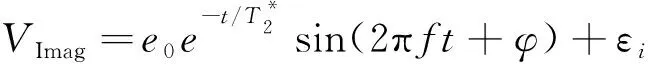
(2)
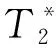
在采集MRS信号时, 环境噪声的影响很大, 其中随机噪声会淹没MRS信号。一般随机噪声服从高斯分布, 其噪声水平根据环境不同达到200 nV以上。对于在MRS数据Vi中的随机噪声, 可以分为加性噪声Vp∈N(μp,σp)和乘性噪声Vm∈N(μm,σm)两类, 分布模型为
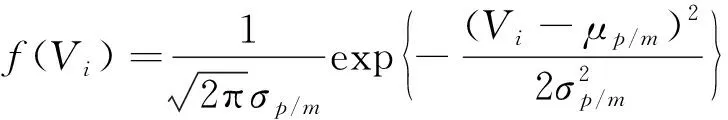
(3)
其中乘性噪声的噪声水平与MRS信号幅度VMRS相关,σmi=|eln(α)Vi|, ln(α)是乘性噪声的系数。因此在受到随机噪声影响后的MRS复包络数据为
Vnoi=VMRS+Vp+Vm
(4)
2 马尔可夫链蒙特卡洛参数提取
2.1 马尔可夫链的蒙特卡洛
MH(Metropolis Hasting)算法是常用的MCMC采样方法之一。MH算法的基本思路是在每步状态由x移动到新的状态x′时, 其概率为q(x′|x),q称为MH算法的建议概率密度分布(也称为转换核), 同时满足以下条件
π(x)q(x′|x)=π(x′)q(x|x′)
(5)
其中π(x)是目标分布(即待采样的分布)。满足式(5)的条件也称为由一条马尔科夫链固定的概率密度函数, 但容易造成该马尔科夫链性质不相等, 因此需要添加额外的参数条件, 即
π(x)q(x′|x)α(x′|x)=π(x′)q(x|x′)α(x|x′)
(6)
其中α(x|x′)定义为状态从x′移动到x的概率;q(x|x′)α(x|x′)称为更新后的建议概率密度分布。为了保证这个式子成立, 可以设α(x|x′)≡1, 得到一次移动的概率为
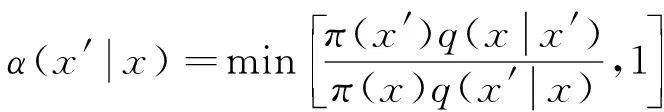
(7)
其中α(x′|x)是状态从x移动到x′的概率, 也称为接受概率。如果建议被接受, 则新状态被赋值为x′, 否则新状态仍为x。
MH算法的实现步骤为:
1) 设s=0, 生成一个初始值x, 即初始状态x(0)=x;
2) 令s∶=s+1;
3) 从建议分布中生成一个建议值x′;
4) 根据式(7)计算接受概率α(x′|x);
5) 从均匀分布U~(0,1)生成一个随机数u;
6) 如果u<α(x′|x), 则令x(s+1)=x′; 反之, 则令x(s+1)=x(s)=x;
7) 循环执行步骤2)~步骤6), 直到s=N(N代表迭代的次数, 保证在马尔科夫链下的目标分布达到平稳分布)。
2.2 参数提取方法
在贝叶斯条件概率的框架下, 通过MRS复包络数据推算参数的问题可以表示为: 在给定观测数据V和参数先验信息M条件下, 估计关于参数的后验分布概率密度函数
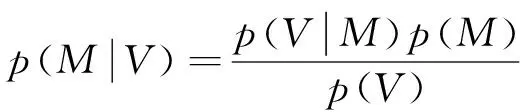
(8)
其中p(V|M)代表似然函数, 表示MRS信号复包络数据与未知参数之间的相互关系;p(M)是参数的先验概率分布;p(V)可认为是一个仅取决于观测数据的常数, 仅对后验分布起到归一化的作用, 因此可以忽略不计。进而在p(V)为定值的条件下有
p(M|V)∝p(V|M)p(M)
(9)
其中后验分布概率函数p(M|V)就是各参数的解。
根据文献[4], 由于噪声服从高斯分布, 而且各参数之间相互独立, 因此似然函数p(V|M)可定义为一种多维的正态分布
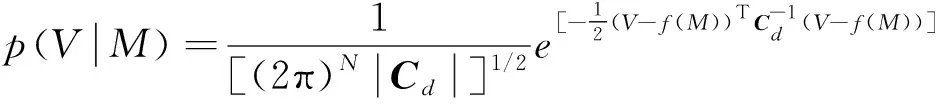
(10)
其中V是MRS复包络观测数据;f(M)是给定参数的MRS复包络表达式的预测数据;N是观测数据的个数;Cd是观测数据的协方差矩阵, 由每个时间点对应的预测值与观测数据误差方差组成的一个对角矩阵; |Cd|表示协方差矩阵Cd的行列式。
通过贝叶斯框架的建立, 可求解出后验概率分布p(M|V), 但由于p(M|V)表达式较为复杂, 抽样维度高, 需要抽样的样本量大, 采用蒙特卡洛的方法完全列举后验分布或对后验分布进行均匀采样都是不符合实际的, 因此这里使用MCMC方法实现后验分布采样。
在计算后验分布时, 其后验概率分布p(M|V)就是上述MH算法中的目标分布π(x), 先验概率分布p(M)即为上述建议概率密度分布。由于建立的先验概率分布模型p(M)服从高斯分布, 具有对称性, 满足p(M′|M)=p(M|M′)。因此化简得到接受概率为
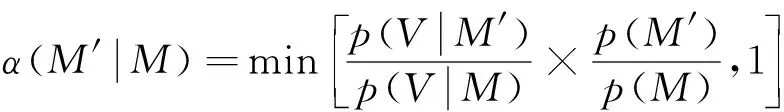
(11)
通过MCMC模型实现MRS复包络参数提取的步骤如下:
1) 对采集得到的MRS数据通过已有方法去除尖峰噪声和工频噪声;
2) 通过希尔伯特变换以及低通滤波处理得到MRS复包络数据V;
3) 设非线性拟合提取MRS复包络各参数, 确定参数的先验信息概率密度分布p(M);
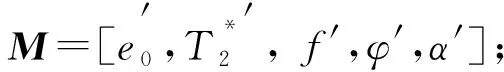
5) 设置迭代次数为N,迭代步长为Δs, 令s∶=s+Δs;
6) 从先验概率分布模型p(M)中生成一组建议参数向量H;
7) 根据式(11)计算接受概率α(H|M);
8) 从均匀分布U~(0,1)生成一个随机数u;
9) 如果u<α(H|M), 则令M(s+Δ s)=H; 反之, 则令M(s+Δ s)=M(s)=M;
10) 循环执行步骤2)~步骤6), 直到s=N, 得到采样后的后验分布函数p(M|V)。
使用MCMC方法采样后验分布的收敛条件,是指采样得到的样本达到稳定状态。在马尔可夫链达到稳定后, 其之前状态得到的数据都会被抛弃。当迭代次数N一定, 如果迭代步长Δs过小, 则会出现无法收敛的情况。在文献[2]中提到了一种初始设置方案, 可选择取链条数为3, 采样迭代次数为1 000 000次, 默认丢弃前50%样本后收敛, 达到稳定。
3 数值模拟
3.1 仿真实验
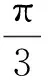
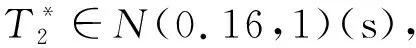
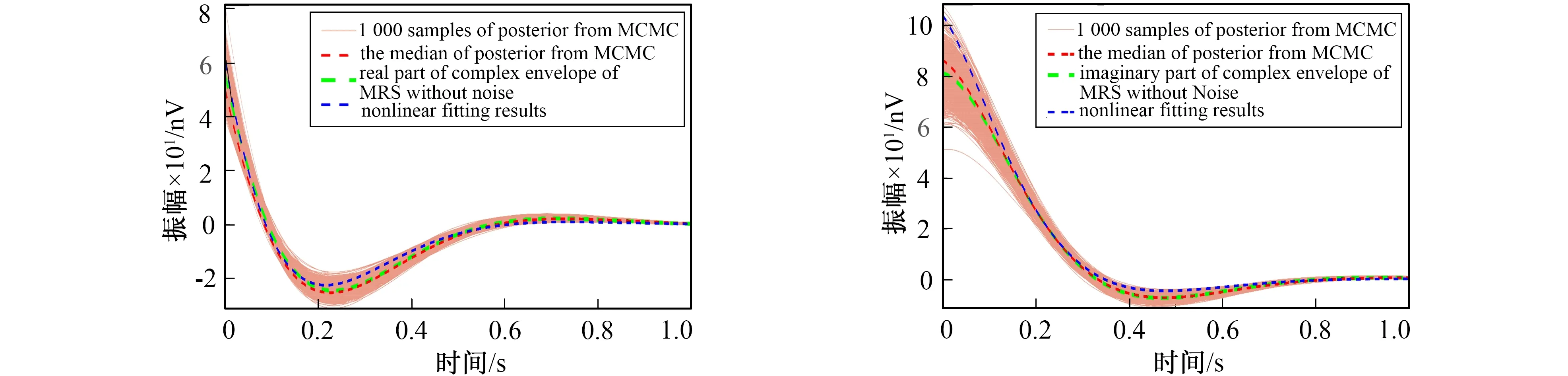
a 包络实部提取结果对比 b 包络虚部提取结果对比图1 非线性拟合、 MCMC拟合结果与无噪声MRS复包络信号对比Fig.1 Comparison of nonlinear fitting, MCMC fitting and noiseless complex envelope of MRS
通过图1可以发现, 当引入乘性噪声后, 非线性拟合效果下降。而通过MCMC方法拟合参数受到的影响较小, 依然维持在较好的拟合效果(见表1)。

表1 参数提取结果对比
3.2 稳定性分析
选取加性噪声水平分别为100 nV、 150 nV、 200 nV和500 nV, 乘性噪声系数为lg(1.5)。在进行多组测量记录结果后, 绘制参数的箱图如图2所示。由图2可见, 在乘性噪声系数一定的情况下, MCMC参数提取方法可以保证结果准确度。随着加性噪声水平增大, 两种方法的参数准确度逐渐降低, 但MCMC方法准确度仍然可以保持稳定。
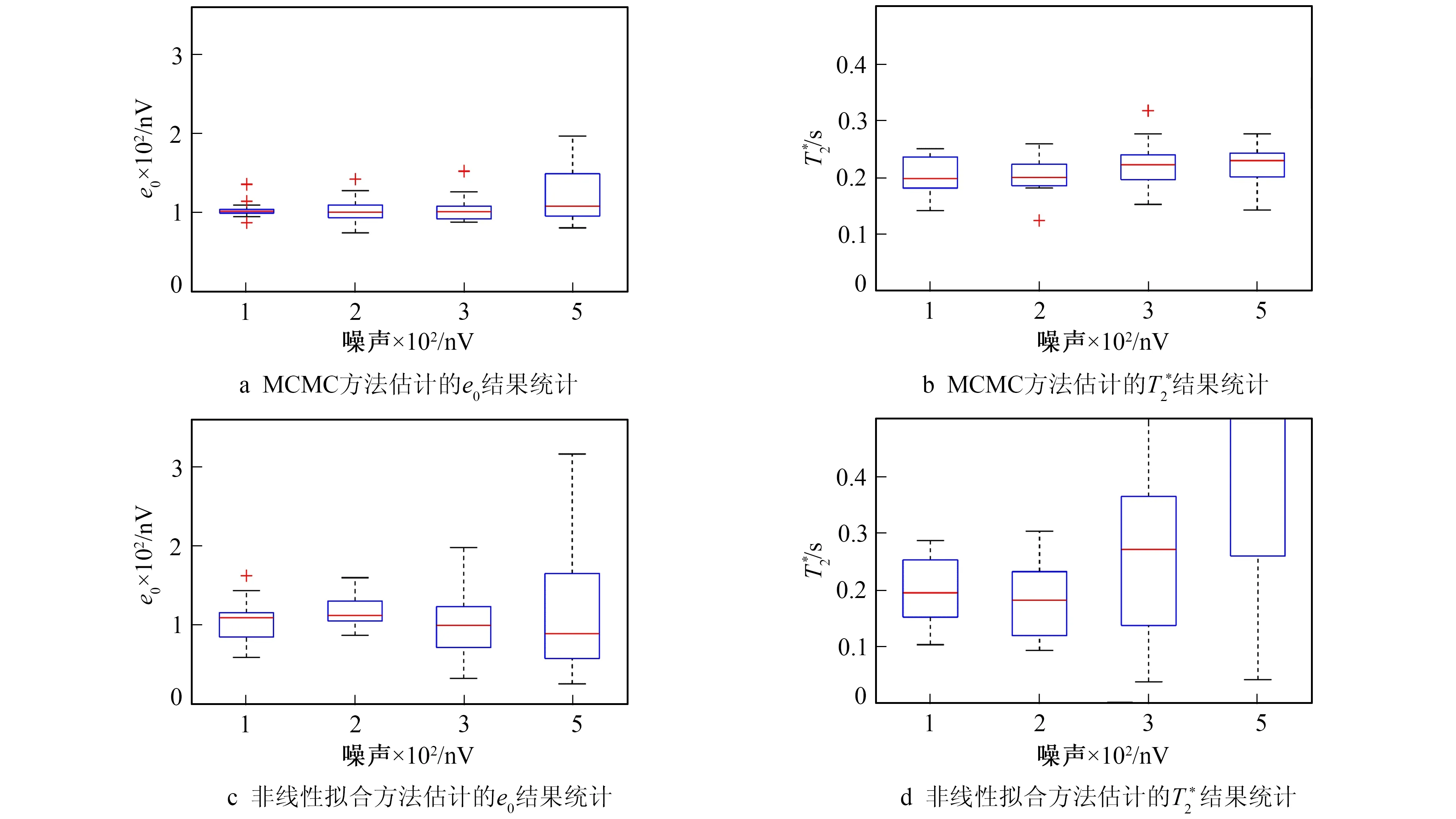
图2 100组仿真数据的MRS包络信号参数提取结果统计Fig.2 100 sets simulation data of parameters extraction from MRS envelope signals
选取乘性噪声水平系数为lg(1.5)、lg(2.0)、lg(3.0)、lg(5.0), 加性噪声水平为100 nV,在进行多组测量记录结果后, 绘制参数的箱图如图3所示。由图3可见, 在加性噪声水平一定的情况下, MCMC参数提取方法可保证结果准确度。随着乘性噪声系数增大,两种方法的参数准确度逐渐降低, 但MCMC方法准确度仍然可以保持稳定。
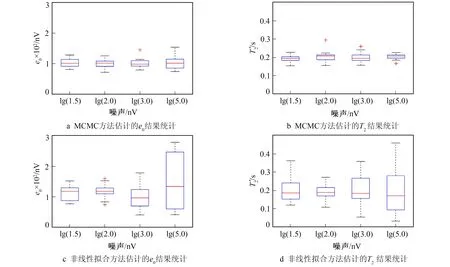
图3 100组仿真数据的MRS包络信号参数提取结果统计Fig.3 100 sets of simulation data of parameters extraction from MRS envelope signals
4 结 语
笔者针对已有利用非线性拟合提取MRS信号复包络表达式参数方法的基础上, 利用非线性拟合的方法, 实现了建立各参数的先验信息分布和参数与数据的似然函数, 通过MCMC方法中的MH算法采样并求解参数的后验分布, 找到后验分布中出现次数最多、 权值最大的数值作为参数最优估计值。在不同加性噪声水平和不同乘性噪声系数的条件下仿真参数提取实验, 将MCMC参数提取方法与非线性拟合结果对比, 数值模拟结果证明, 在乘性与加性随机噪声的影响下, MCMC参数提取方法优于非线性拟合参数提取结果。
综上, 基于马尔科夫链蒙特卡洛的地面磁共振信号参数提取方法可以有效减少了由于非线性拟合无法处理乘行噪声所带来的误差。虽然需要的运算时间变长, 但保证了参数的估计精度与稳定性, 即解决了乘性噪声和加性噪声共同影响参数提取的问题。

