基于智能算法的灾区救援路径规划
周小琳, 焦子恒, 胡锦林, 李彦怡, 王长鹏
(1. 长安大学 a. 信息工程学院; b. 理学院, 西安 710000; 2. 宝鸡文理学院 经济管理学院, 陕西 宝鸡 721013)
0 引 言
21世纪以来, 世界各地灾害频发, 使各国人民遭受了巨大的生命威胁和经济损失, 越来越多的学者进行应急救灾的模型构建及研究, 随着科技的发展, 智能算法在各行各业中得到了广泛应用。2017年, 美国波多黎各[1]遭受了最严重的飓风灾害, 致使该岛的人员伤亡和经济损失极为惨重, 交通网络的大部分功能丧失。由于持续严重受灾, 波多黎各的城镇情况在相当长的一段时间内十分不明朗, 救援无法进行; 数十个地区孤立且无法通信。各地区对医疗用品、 救生设备的需求量急剧增大, 对紧急救护诊所、 医院急诊室和非政府组织救济行动的需求也急剧增大。在灾情期间, 一个非政府组织HELP, Inc.试图通过设计一种名为“DroneGo”的灾难响应系统[2]减少灾害造成的损失。DroneGo将使用旋翼无人机提供预先封装的医疗用品和高分辨率航拍视频侦察, 以进行医疗救援和提供交通道路网络的破坏情况等相关信息。
针对急缺电力、 水源、 救灾物资的重大灾难突发地, 笔者建立了利用现代无人机和救援集装箱进行首要物资的分配以及受损交通干线侦测的灾难相应模型, 其中急需解决的任务有(以美国波多黎各受灾为例): 结合人口分布和地理位置, 确定集装箱放置的最佳位置[3], 以便能进行医疗供应交付和道路网络的视频侦察; 形成最佳的无人机调度时间表[4], 以满足侦查和物资配送需求。
当灾情发生后, 如何及时、 有效、 合理地把各个储备点有限的救灾物资分配到灾区的各个物资发放点, 成为应急管理部门非常关心的一个重要问题, 也是国内外学者研究的一个热点。目前, 现有针对救灾物资分配问题的研究大致可以粗略地分为单目标优化和多目标优化两大类。
在单目标优化方面, 王冬冬等[5]以救灾物资配送路径最短为目标建立期望最短模型和α最短路径模型。模型将灾区救援物资配送上的不确定因素, 使不确定权重下的灾区救援物资配送问题得到解决。李永义等[6]以最优分配策略为目标建立物资分配优化模型。引入区间数可能度概念, 对灾区区域大小、 受灾程度、 人口密度和灾区群众需求等不确定因素进行区间化, 简化了计算过程, 同时使应急物资的分配量分布更为均衡。
在多目标优化方面, 夏红云等[7]利用前景理论建立了一个以最短应急总响应时间、 最小灾民心理恐慌度、 最小救灾物资为满足度、 最小灾民心理嫉妒值、 最小灾民损失及最小应急响应总成本为目标的救灾物资高纬度多目标分配模型。运用SPEA2+SDE算法进行求解, 并对SPEA2+SDE算法进行了改进, 引入个体编码方案和个体修正策略, 后称SPEA2+SDE+AIR算法, 增强了算法的收敛性能。王挺等[8]根据配送车辆通行时间最小和风险最小为目标建立震后多目标路径优化模型。
针对以上问题, 笔者做了以下工作:
1) 引入泰森多边形进行不同等级的救援响应。引入泰森多变形排除了地势较高、 人烟稀少的地区, 优先搜救人口以及公路网密集区域, 增加模型的实用性。
2) 基于K-means的救援中心预选。利用K-means聚类模型在泰森多边形完成后的结果上进行聚类, 选出更加合理的救援中心投放物资, 增加救援效率。
3) 基于遗传算法的多点式最小搜救路径规划。通过智能遗传算法完成多源有约束的最短搜索路径规划。
1 符号说明

2 基于K-means的聚类模型
2.1 泰森多边形模型
在实际救灾中, 应该首先针对5所医院、 公路网密集、 人口密度大以及平原地区进行救助, 从而确定集装箱位置的选取以及救助与侦察路线的规划。具体如图1所示。
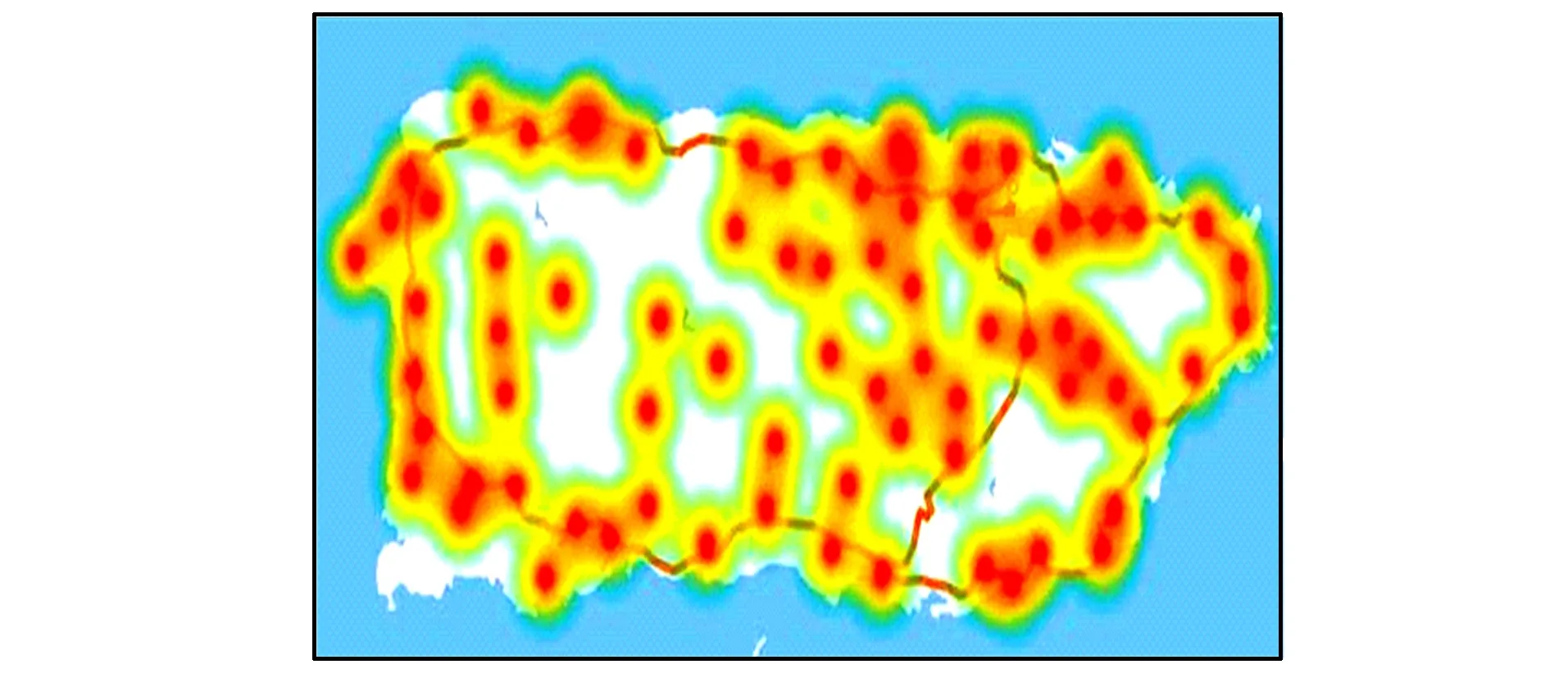
图1 人口热力图Fig.1 Population heat map
图1中粗点表示人口密集区域。从图1中可以直观地看到波多黎各的人口分布情况: 沿海地区和东部地区的人口分布较为密集, 中部较为稀疏。
笔者将这些信息在地图上以离散点的形式呈现出来, 以这些信息为依据利用泰森多边形模型[9]对点进行划分, 从而筛除高海拔山地区域。
画出所有点的垂直平分线, 交叉后会形成很多泰森多边形。每个多边形中仅含有一个离散点, 且该区域所有点到相应离散点的距离最近, 故可用离散点的性质代替整个区域的性质。由此可以对平原地区和高海拔山地区域进行划分。
2.2 K-means聚类模型
运用K-means聚类算法[10], 以无人机最大飞行半径Rm作为聚类的标准, 将筛除山脉的地图聚成3类, 且所有医院必须包括在聚类以内。最后的聚类中心作为集装箱的位置。基于上述分析, 可建立聚类模型。
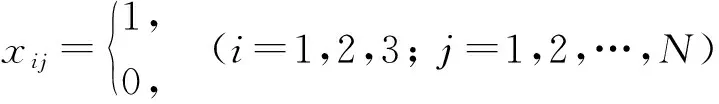

(1)
第j个点到聚类中心距离小于最大飞行半径Rm, 可表示为

(2)
聚类的目标是覆盖率达到最大, 可表示为
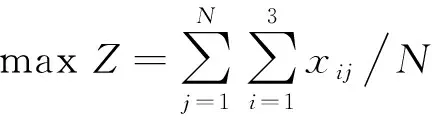
(3)
2.3 算法设计
为了实现符合实际要求的快速搜索规划, 结合K-means中心聚类以及泰森多边形实现算法, 算法如下。
算法1
Input: 人口分布dataloc,聚类阈值thre
Initialize:
随机选择聚类中心center0;
Do:
对每个点计算与center0的距离d;
根据d划分dataloc为k个集合;
计算k个集合的中心centerk;
While: |centerk-center0|≥thre
利用泰森多边形对聚类结果进行筛选;
再进行聚类获得输出结果area1、area2、area2
Output。
运用K-means算法对地图中的点进行聚类, 然后用聚类中心代替地图中的点以达到对地图中的点离散化的效果; 运用泰森多边形对离散化后的点进行划分, 从而筛选出地图中的高海拔山地区域, 并排除; 运用改进的K-means算法对地图中剩下的点进行聚类。以点的最大覆盖率为目标进行聚类中心的搜索。
3 基于遗传算法的多人最短路径模型
3.1 模型分析
在第2节中求出了集装箱的最佳投放位置, 并通过泰森多边形算法将区域离散化, 将问题转化为从离散数据中找出满足约束条件的路径。
已知离散化数据分布, 求解出通过这些点最少1次情况下的最短路径, 这便是经典的旅行商问题。而无人机有航程约束, 因此路径肯定不止1条,所以采用解决基于遗传算法[11]的多旅行商问题[12]的解法求出无人机搜索路径。
3.2 模型建立
无人机全部的搜索范围可看作加权图G, 求出每台无人机的搜索区域, 即求解其顶点集的分组V1,V2,…,Vn在G中生成的n个子图G(V1),G(V2),…,G(Vn), 显然

(4)
无人机完成侦察任务后要返回集装箱充电。设原点为O, 且
O∈Vi,i=1,2,…,n
(5)
设Ai(i=1,2,…,n)为G(Vi)中无人机飞行的最佳路线,ω(Ai)为Ai中所有边的权之和。要使所有无人机的飞行路径之和最短, 则有
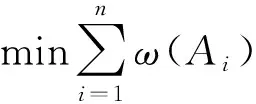
(6)
3.3 算法设计
下面以无人机路程之和最小为优化目标, 运用遗传算法对其进行优化求解。
已知起点和需要经过的点, 同时每条路径都有长度限制, 因此需要对多人旅行商问题的解决方法进行调整改进, 增加每条路径长度小于无人机最大航程的约束条件。
算法2
Input: 无人机数量ndrone,聚类阈值thre
Initialize:
Do:
在区域内随机生成N组点;
根据ndrone数生成断点数ncut;
根据断点数ncut生成N组不同的断点;
对每一组根据对应的断点进行分断,并计算全部路径的距离总和;
生成初始群体gini;
Do:
For every 8 groups:
找出最佳的一组, 对其进行复制操作;
并在复制出来的个体当中进行不同的交叉操作和小概率的变异操作;
生成出新的8个个体, 代替原来的8个个体
如果更优则替换
While: 满足遗传代数
While: 存在某路径长度大于无人机的最大航程;
Output: 最少无人机数下的路径最佳划分。
4 模型求解
4.1 集装箱的最佳位置确定
根据波多黎各人口热力图和交通网络图等实际情况, 将其地图离散化, 如图2a所示, 以便后续求解。其中实心圆代表具有原始人口热力值等信息的点, 空心圆代表离散化后的点。利用泰森多边形得到区域划分, 如图2b所示。

a 离散化数据 b 泰森多边形区域划分 图3 K-means聚类图 图2 初始化数据图 Fig.3 K-means clustering diagram Fig.2 Initialize data
可以直观地看到, 面积较小的泰森多边形为人口较密集和交通线路较密集的地区, 面积较大的泰森多边形可视为海拔较高的山地区域, 可以从地图中剔除, 同时泰森多边形将区域均匀地划分为了较小的区域, 可以用区域中心的点代替整个泰森多边形, 便于后续的集装箱区域划分和路径规划。根据所建模型, 可得到如图3所示的聚类结果。
不同颜色的点代表不同的聚类, 实心点代表聚类中心。可以得到集装箱的位置在[18.383,-67.005],[18.302,-66.406],[18.301,-65.9], 可以覆盖81%的岛屿面积。可见, 运用K-means聚类模型可以较好地选取集装箱的最佳位置, 使其覆盖范围最大。
4.2 无人机的交付路线和侦察路线
根据所建模型, 得到了无人机最优的侦察路线, 如图4所示。发现无人机都是绕一个极窄的类似椭圆的路线最后返回集装箱位置, 总体上看无人机的侦察路线图呈辐射状。
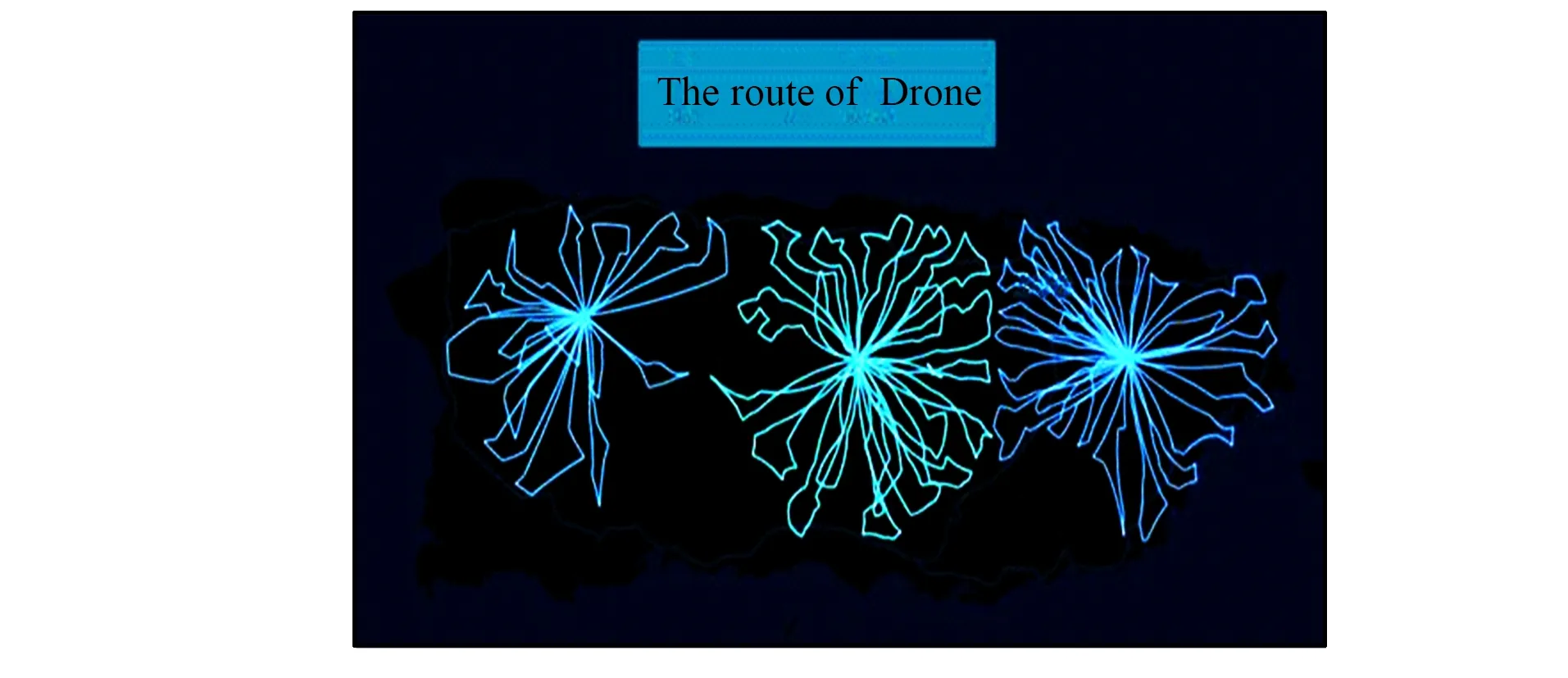
图4 无人机最优侦察路线图Fig.4 Optimal uav reconnaissance roadmap
5 灵敏度分析
下面对模型中的一些参数进行调整[12], 以验证所建模型的合理性和稳定性。
首先研究遗传算法的迭代次数对结果的影响, 如图5所示。由图5可知, 迭代次数较低时, 算法得到的结果很差; 迭代次数越高, 遗传算法获得的路径越短, 无人机进行侦察的时间越短, 但相应的算法收敛时间越长。而迭代次数增加到一定数值时, 路径总和的变化幅度很小。所以需要合理地调整迭代次数。且无人机数量较少时, 侦察用时很长; 此时增加无人机数量, 侦察用时急剧下降, 模型的灵敏度较高, 故无人机的数量对模型的影响较大, 因而需要选取合理的集装箱装载方案。
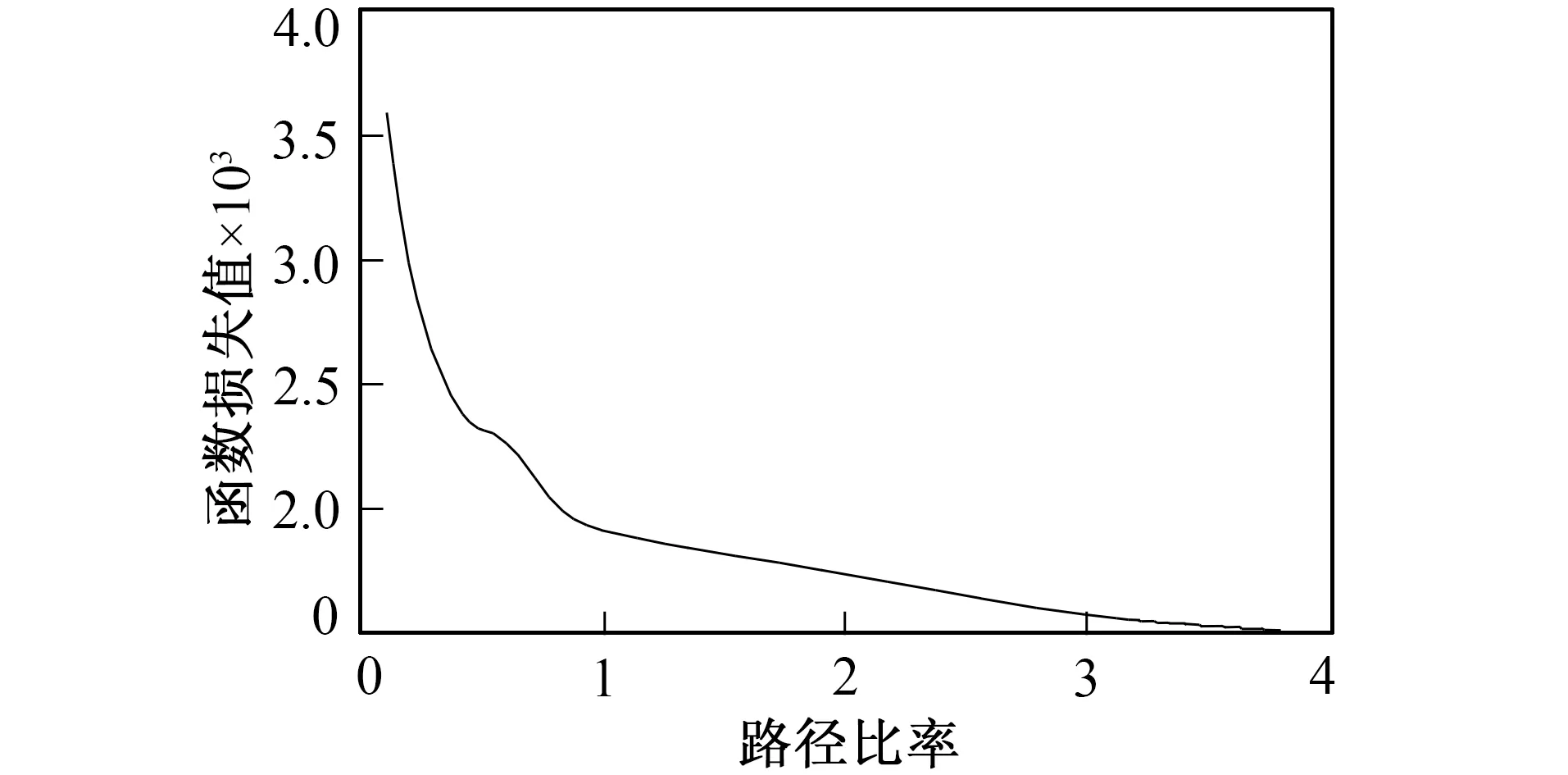
图5 遗传算法的灵敏度分析Fig.5 Sensitivity analysis of genetic algorithm
基于上述分析, 可以得知笔者建立的模型能很好地应用于实际问题, 模型的稳定性较好。
6 结 语
通过结合智能算法和泰森多边形建立灾区响应救援模型, 利用泰森多边形, 以公路网密集程度、 人口密度等为标准以点代面, 筛除高海拔地区, 建立了基于遗传算法的多旅行商模型, 采用多目标全局最优启发式搜索策略, 很好地求得了无人机的飞行最短路径, 同时以美国波多黎各受灾区域为例, 成功检验了模型在实际中的有效性。

