北斗卫星整网集中式自主定轨算法研究
林 夏, 林宝军,5, 刘迎春 , 白 涛, 武国强, 王正凯
(1. 上海微小卫星工程中心 导航卫星研究所, 上海 201210; 2. 中国科学院 空天信息创新研究院, 北京 100094; 3. 中国科学院大学计算机科学与技术学院, 北京 100094; 4. 中国科学院 微小卫星创新研究院, 上海 201210; 5. 上海科技大学 信息学院, 上海 201210)
0 引 言
北斗三号卫星通信系统将于2020年全面建成, 为全球提供导航服务[1]。相比于北斗二号卫星, 北斗三号卫星均增加有星间链路载荷, 以实现北斗导航星座中双星间的测距与通信[2-3]。与GPS卫星采用的UHF链路不同, 北斗卫星采用Ka星间链路。相比于UHF链路, Ka链路建链速度更快, 抗干扰能力更强, 是一种性能更为优越的星间链路设计。基于Ka星间链路的星间测距及通信能力, 新一代北斗卫星均设计有自主导航功能。通过实时采集星间、 星地双向测距信息, 可实现对卫星动力学预报轨道的修正, 进而实现卫星自主导航。但与GPS卫星一样, 北斗卫星也采用分布式算法以实现卫星星间测距自主导航。在分布式算法中, 算法只获取与本星相关的星间测距值, 仅根据星间测距值确定自身导航状态。由于分布式算法是以假设解耦为前提的, 其精度将不可避免地遭受损失[4]。
与分布式算法估计方法不同, 集中式算法是采集整网卫星星间测距信息, 并基于测距信息确定所有星座卫星的导航信息, 得到全局最优解。因而, 从统计学角度分析, 集中式算法精度远优于分布式算法。地面即是通过集中式批处理算法实现卫星轨道的精密确定。近年来, 毛悦等[5]为降低集中式自主定轨算法的计算量, 提出了一种以长期预报星历为基础, 利用观测信息实时修正广播星历变量的集中式自主定轨方法。陈艳玲等[6]和谢金石[7]提出了一种快速、 稳定的运动学集中式定轨算法。该算法不基于轨道动力学模型, 利用高阶多项式对真实轨道与长期预报星历的差异进行描述。上述学者虽分别设计了星上可用的集中式导航算法, 但均以星上处理能力受限为前提, 将算法进行了相应的简化。而随着北斗三号卫星在星载计算机和星间通信技术的突破, Ka星间链路可以实现卫星与卫星之间100 kByte的通信速率, 而星上使用的龙芯1E300处理器的处理能力最高可达到200 MIPs。因而, 笔者认为仅需将推广卡尔曼滤波算法代替地面传统的批处理算法, 并合理设计算法工程实现流程, 即可实现集中式导航算法的在轨使用。
为此, 笔者设计了一种基于推广卡尔曼滤波算法的整网集中式定轨算法, 并设计了算法的实现流程。同时, 为评估算法是否受星上处理能力制约, 特将算法注入星上使用的龙芯1E300处理器中进行仿真测试, 在评估算法精度的同时也验证算法的工程可行性。
1 基于推广卡尔曼滤波的集中式自主导航设计方法
笔者设计的基于推广卡尔曼滤波的集中式导航算法是以卫星动力学模型产生的外推轨道作为一步预报, 星间双向测距值作为观测量, 推广卡尔曼滤波法作为估计方法的导航算法。因而, 下面将对卫星动力学模型, 星间测距观测模型以及推广卡尔曼滤波估计模型分别进行阐述。
1.1 卫星动力学模型
卫星动力学模型可表示为

(1)
其中r为卫星在惯性坐标系中的位置矢量;v为卫星在惯性坐标系中的速度矢量;a(r,v,t)为卫星受各种作用力而产生的加速度。
由于北斗卫星为中高轨卫星, 卫星主要受地球二体引力, 非球形摄动力, 日月三体引力和光压摄动力作用。因而, 对卫星所受加速度a(r,v,t), 可利用表1中轨道信息预报模型构建。同时, 由于算法采用推广卡尔曼滤波算法, 卫星动力学模型中还需对轨道状态转移矩阵预报模型进行设计。如表1所示, 轨道状态转移矩阵仅考虑二体中心引力与J2非球形摄动模型, 具体算法参见文献[8]所述。

表1 卫星动力学建模方法
1.2 星间测距观测模型
集中式定轨算法是以星间双向测距信息作为观测量并构建观测方程实现星座卫星自主定轨。下面对算法的观测量及观测方程实现方法进行描述。
卫星星间双向测距原始信息可由
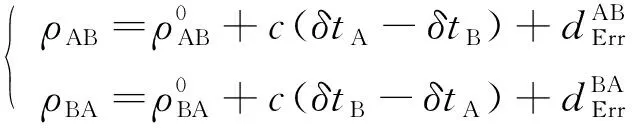
(2)
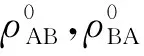
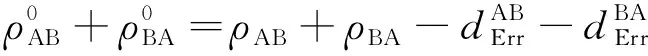
(3)
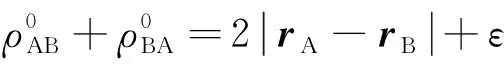
(4)
其中rA,rB分别为卫星A,B的位置向量。
将方程等号右侧式子进行一阶泰勒公式展开, 即可得到观测方程
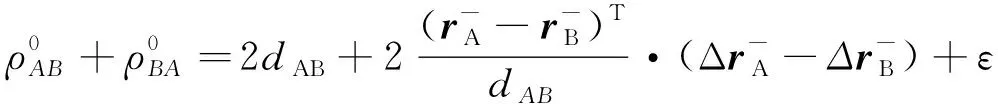
(5)
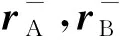
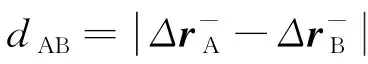
(6)
1.3 推广卡尔曼滤波算法估计模型
在地面采用集中式导航算法计算导航星座各星精密轨道时, 一般采用最小二乘批处理估计方法。最小二乘批处理方法存在着实时性差, 计算量大等缺点。因而, 为实现集中式导航算法星上使用, 笔者选择推广卡尔曼滤波算法估计方法。
具体而言, 设定X=[r,v], Δx=[Δr,Δv], 其滤波过程可由初始化

(7)
状态估计
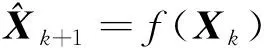
(8)
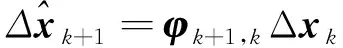
(9)
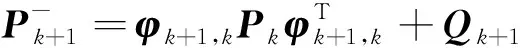
(10)
测量更新
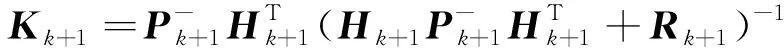
(11)
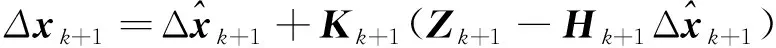
(12)
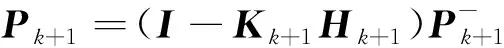
(13)
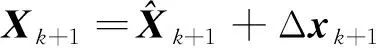
(14)

2 集中式自主导航算法的在轨实现方法
要使集中式导航算法在轨稳定运行, 除建立算法设计方法外, 还需对算法的在轨实现流程加以设计。具体而言, 若要在北斗卫星上实现集中式定轨算法, 需首先基于星座建链表完成整网卫星间的相互测距。而后, 依据星座路由表, 将测距值传入星座卫星中所设的主节点卫星。接着, 主卫星运行集中式导航算法, 利用整网星间测距信息得到整网星座卫星轨道信息。最后, 主卫星将所更新的导航信息传入各个子卫星, 实现各卫星轨道信息的更新。
根据北斗卫星目前星间测距能力, 3 s即可完成双星间的相互测距, 因而30 s内即可完成本星与最多10颗卫星的相互测距。且北斗卫星Ka星间链路最高可以实现卫星与卫星之间100 kByte的通信速率, 也为将整网测距信息传入主卫星提供了可能。因而, 若规定算法周期为5 min, 可设计如图1在轨实现流程。
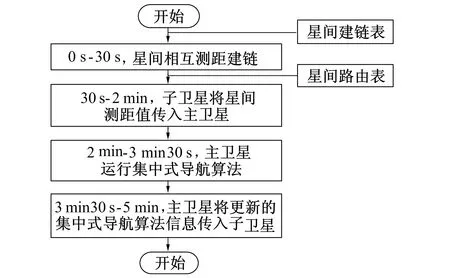
图1 集中式自主导航算法的在轨实现流程Fig.1 The flow chart of the centralizedautonomous navigation algorithm
3 仿真验证
由于文献[10]指出星载处理器数据处理能力的限制是制约星上使用全星座自主导航算法的主要因素, 因而笔者将算法注入于龙芯1E300处理器中, 以星上使用的龙芯1E300处理器为硬件基础, 进行集中式导航算法的仿真验证。龙芯1E300处理器是由中科龙芯公司最新研发的宇航级处理器, 并已在北斗卫星CA34,CA35中使用。龙芯1E300处理器的峰值频率可达200 MHz, 可用内存达512 Mbit。通过在龙芯1E300处理器中验证集中式导航算法, 可对算法的精度, 稳定性及在轨应用可行性均进行评估。
3.1 仿真条件
依据北斗星座卫星运行特点, 构建24颗北斗MEO星座卫星仿真轨道。设定仿真周期为30 d, 星间测距周期为5 min, 星间测距精度为0.1 m。整网卫星单星平均链路数为8条。有1个地面锚固站参与定轨, 周期内锚固站与4颗在轨卫星建链。算法注入于龙芯1E300处理器上运行, 以评估算法周期内所需时间。
3.2 仿真结果
首先, 由于集中式自主导航算法是以星上动力学一步轨道预报信息为基础的导航算法, 为更好评估算法定轨精度, 对预报轨道精度进行分析。图2为采用1.1节所述轨道动力学预报方法, 30 d整网卫星轨道预报URE平均误差。由图2可见, 由于预报模型与真实轨道存在偏差, 导致卫星轨道预报误差缓慢发散, 到30 d时, 误差可达 330 m。
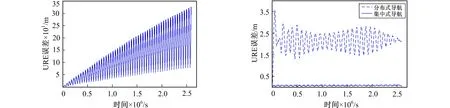
图2 整网卫星轨道预报平均 图3 卫星整网集中式分布式导航 URE误差 算法轨道平均URE误差 Fig.2 The average URE of the Fig.3 The average URE errors of the centralized Beidou satellites navigation algorithm and the distributed navigation algorithm
图3给出了集中式与分布式整网卫星平均URE误差仿真结果。而后, 依据3.1节所述仿真条件, 对算法定轨精度进行验证。为充分评估集中式算法精度, 笔者在相同的仿真条件下, 对采用分布式算法的估计精度进行评估。由图3可见, 集中式定轨算法整网卫星平均URE误差仅为0.18 m, 远优于分布式导航算法2.8 m的平均URE轨道误差。
最后, 由于算法在龙芯1E300处理器中运行, 算法的工程可行性也相应得到了验证。经仿真评估, 周期内, 龙芯1E300处理器57 s可生成整网卫星定轨结果, 可满足第3节中算法实现方法要求。
4 结 语
笔者对北斗卫星整网集中式定轨算法在轨实现方法进行研究, 设计了基于推广卡尔曼滤波的整网集中式导航算法方法, 并基于北斗卫星Ka星间链路载荷及龙芯1E300处理器设计了算法的星上实现流程。将算法注入于龙芯1E300处理器中, 通过集中式导航算法的仿真验证表明, 利用笔者设计的整网集中式导航算法, 整网卫星URE精度为0.18 m, 远优于分布式导航算法整网URE精度2.8 m。且周期内, 龙芯1E300处理器用时57 s即可完成算法处理, 可充分满足星上使用要求。

