基于K-CV优化的PCA和SVM人脸识别算法

林志谋

(厦门海洋职业技术学院 信息技术系, 福建 厦门 361012)

0 引 言

人脸识别在经济、 交通、 旅游和法律等行业有着广泛的应用, 国内外学者对其进行了深入的研究。目前人脸识别技术主要有3种类别: 基于几何特征的方法[1]、 基于模板的方法[2]和基于模型的方法[3]。常规的PCA(Principal Component Analysis)和SVM(Support Vector Machines)人脸识别算法存在计算简单, 通用性强等优点, 但SVM参数的取值制约着人脸识别算法的精度, 有些参数寻优算法效率不高导致该人脸识别算法的实用价值不高。

笔者提出利用交叉验证方法(K-CV:K-fold Cross Validation), 同时使用改进的网格搜索方法[4]改进常规算法。其主要思路是先确定一个较大的范围, 在此范围内用较大的步距, 确定一个较小的最优参数区间, 然后在这个最优区间范围内, 再用小步距进行精确搜索。对比常规的网格搜索的方法, 明显减少了搜索SVM最优参数的时间, 提高了搜索效率。再将样本数据作为训练集, 尽可能消除由于个别样本误差对预测模型的影响, 同时联合了PCA和SVM[5]的人脸识别算法, 使人脸识别算法更好地满足实时性的要求, 解决了常规的PCA和SVM人脸识别算法性能不好的问题, 提高了人脸识别的准确率。

1 识别算法原理

1.1 PCA算法主要原理

主成分分析方法(PCA)[6]主要用于图像数据的降维。利用PCA算法可较大幅度地降低人脸数据特征的维数, 减少图像中冗余的信息和噪声, 又能保留有效的识别信息[7]。

假设有n个d维空间中的样本x1,x2,…,xn, 其中xi=(xi1,xi2,…,xid)T∈Rd, 假设X为这n个样本构成的数据矩阵, 即X=(x1,x2,…,xn)。假定需降到m维, PCA算法对数据降维处理流程如下：

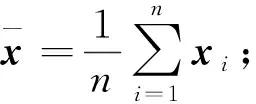
3) 计算S的前m个最大特征值, 并按大小进行排序, 即λ1≥λ2≥…≥λm,ψ1,ψ2,…,ψm,ψj(j=1,2,…,m)∈Rd为其对应的特征向量, 构成矩阵φm=(ψ1,ψ2,…,ψm);

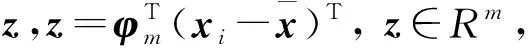
利用PCA算法可降低人脸数据的维数及运算的复杂度, 进而可利用SVM算法,对提取得到的人脸数据进行分类处理。

1.2 SVM算法主要原理

支持向量机(SVM)可支持线性和非线性的分类。其主要原理是把数据映射到一个高维空间上使数据变稀疏,比较容易找到一个分割面将数据分类,该高维分割面就是超平面。SVM算法的主要目的是找到一个使数据点离该超平面尽可能远的超平面, 通过该超平面进行分类的效果较好。人脸识别是典型的非线性支持向量机分类问题,分类的主要流程如下[8]。

假设输入的训练数据T={(x1,y1),(x2,y2),…,(xm,ym)}, 其中xi∈Rn,yi∈{-1,1},i=1,2,…,m。

1) 选择核函数K(xi,yi)和惩罚参数C, 构造并求解最优化问题

使用二次规划法, 求得最优解

2) 计算向量w*和截距b*,w*计算公式如下

b*可通过满足

的样本求得。

3) 获得最优分类面函数

f(x)=sgn{(w*·x)+b*}

笔者采用的核函数是目前应用广泛且效果良好的高斯径向基核函数, 该函数适用于小样本或大样本数据的情形, 也适用于高维或低维数据的情形, 其表示形式如下

K(xi·x)=exp(-g‖xi-xj‖2),g>0

其中g是核函数参数。

惩罚系数和核函数参数影响SVM分类器的性能。SVM算法用于人脸识别时, 要得到满意的结果, 需调整相关的参数, 才可得到更高的人脸识别精度。采用CV(Cross Validation)的思想和改进的网格搜索方法比随机选择参数训练SVM得到的模型在人脸识别精度上更高。

2 基于K-CV优化算法对SVM参数寻优

K-CV算法优化SVM相关参数, 其方法是将原始数据分成K组, 并将每个子集数据分别做一次验证集, 其余的K-1组子集数据作为训练集, 可得到K个模型, 用这K个模型最终的验证集的分类准确率的平均数作为此K-CV算法下分类器的性能指标。传统的网格搜索方法每个网格都是均分的, 有计算量大的缺陷, 笔者提出了用改进的网格搜索方法提高其性能。

改进的网格搜索方法优化SVM参数的方法如下： 惩罚系数参数c和核函数参数g先采用大步距大范围的粗略搜索, 确定一个初始的最优参数区间, 然后在这个最优区间再小步距精确搜索, 最终得到最优化的参数, 这种方法减少了计算量。SVM参数寻优算法主要流程图如图1所示。

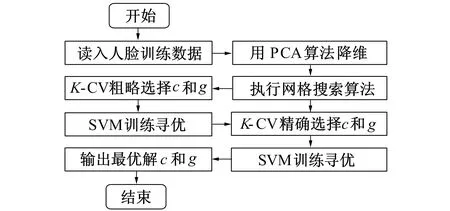
图1 参数搜索流程图Fig.1 Parameter search flow chart

3 算法实现流程

为验证基于K-CV优化的PCA和SVM人脸识别算法, 需利用Matlab软件进行仿真测试。Lin[9]开发设计的集成库LIBSVM内置了训练函数和预测函数, 可用其实现SVM算法。笔者采用ORL(Olivetti Research Laboratory)人脸库进行算法验证, 其含有40人总共400张人脸的图像样本, 将其分成两组, 用前8张人脸图片作为SVM模型训练样本, 后2张图片作为SVM模型预测的样本, 算法的主要流程如下：

1) 读入ORL人脸库所有的图片, 分别用作训练样本和预测样本;

2) 对人脸数据库的训练样本用PCA算法降维, 并提取人脸图像的特征向量；

3) 先确定最优的分组数目K, 再采用基于K-CV算法和改进的网格搜索方法寻找得到SVM参数的最优解；

4) 将步骤2)得到的人脸图像的特征向量和步骤3)得到的参数最优解, 输入到SVM分类器中进行训练识别；

5) 对人脸数据库的训练样本用PCA算法降维, 提取人脸图像的特征向量, 然后输入SVM测试函数进行预测；

6) 比较SVM测试函数产生的标签和预测样本的人脸图片的标签, 获得人脸识别的准确率。

算法的伪代码表示如下：

%数据初始化

bestAccuracy=0;

bestc=0;

bestg=0;

%读取训练用的人脸数据

[train_X train_label]=read_face_data();

%对人脸数据PCA降维

[train_data train_S]=pca_face_feature(train_X, train_label);

%对c和g划分网格搜索

for c=2^(cmin): 2^(cmax)

for g=2^(gmin): 2^(gmax)

利用K-CV算法, 将训练数据平均分成K组, 设为train_data(1), train_data(2)…train_data(K)； 将训练标签也平均分成K组, 设为train_label(1),train_label(2)…train_label(K)

for time=1:K

让train_data(time)作为训练集, 其他作为验证集

记录本次的验证准确率为acc(time)

libsvm_svmtrain()

end

cv=(acc(1)+ acc(2)+…+acc(K))K;

if(cv>bestAccuracy)

bestAccuracy=cv;bestc=c;bestg=g;%记录最佳的c和g

end

end

end

%读取测试用的人脸数据

[test_X test_label]=read_face_data();

%对人脸数据PCA降维

[test_data test_S]=pca_face_feature(test_X test_label);

%把得到的最佳参数输入SVM测试函数进行预测, 并获得人脸识别的准确率

libsvm_svmpredict();

算法中的cmin,cmax,gmin,gmax,K事先给定, bestc和bestg记录最佳的SVM参数, bestAccuracy记录最高的精度。

4 实验结果和分析

4.1 确定最优的分组数目K

首先读入ORL人脸库用作训练样本的人脸图片, 采用PCA算法对训练样本降维并提取人脸图像的特征向量, 结合K-CV算法对SVM模型参数进行优化, 得到人脸识别精度随K值的变化如表1所示。由表1可见,K≥6时, 人脸识别准确率达到最大值97.812 5%, 为降低运算复杂度, 笔者选择K=6。

表1 识别准确率随K值的变化结果

4.2 确定惩罚系数c和核函数参数g

笔者采用K-CV算法和改进的网格搜索方法确定最优化SVM参数。图2是采用大步距粗略搜索的等高线图, 横坐标和纵坐标分别代表参数c和g取以2为底的对数后的取值范围, 等高线代表取相应的c和g后对应的K-CV算法的人脸识别准确率。图3是采用大步距粗略搜索的3D视图, 其中c和g的范围都设置为[2-20,220], 步距设置为0.8, 得最优的惩罚系数c=3.031 4, 核函数参数g=0.002 243 6, 最佳的人脸识别准确率为97.812 5%。由图2可见,c的范围可缩小到[2-5,23],g的范围可缩小到[2-10,20], 步距设置为0.1。在上面粗略选择的基础上可再进一步利用SVM训练函数进行精细的参数选择, 以减少大量不必要的计算, 节约时间； 反之, 如果一开始就采用小步距搜索, 将耗费很多时间。小步距参数选择等高线图如图4所示, 其3D视图如图5所示。由图4和图5可见, 经过小步距的精细参数选择后, 得最优的惩罚系数c=2.639, 核函数参数g=0.002 577 2, 最佳的人脸识别准确率是98.125%。

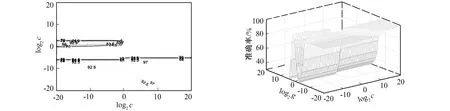
图2 大步距参数选择等高线图 图3 大步距参数选择3D视图 Fig.2 Big step parameter selection contour map Fig.3 Big step parameter selection 3D view

图4 小步距参数选择等高线图 图5 小步距参数选择3D视图 Fig.4 Small step parameter selection contour map Fig.5 Small step parameter selection 3D view

4.3 与传统网格算法寻优时间比较

在最优的分组数目K=6的条件下,c的范围都设置为[2-3,23],g的范围都设置为[2-10,2-7], 步距都设为0.1, 针对传统网格算法和改进的网格算法, 分别做5次实验, 求出平均寻优时间, 如表2所示。由表2可见, 在相同识别准确率的情况下, 改进的网格搜索算法明显优于传统的网格搜索算法。

表2 与传统网格算法寻优时间比较

4.4 与其他人脸识别算法比较

利用得到最优惩罚系数c和核函数参数g, 对SVM进行训练和分类预测。将人脸图像测试集的实际分类和预测分类结果进行比较, 在测试集的40人共80幅人脸图像中, 预测错误的有3幅图像, 人脸识别的准确率为96.25%(见图6)。

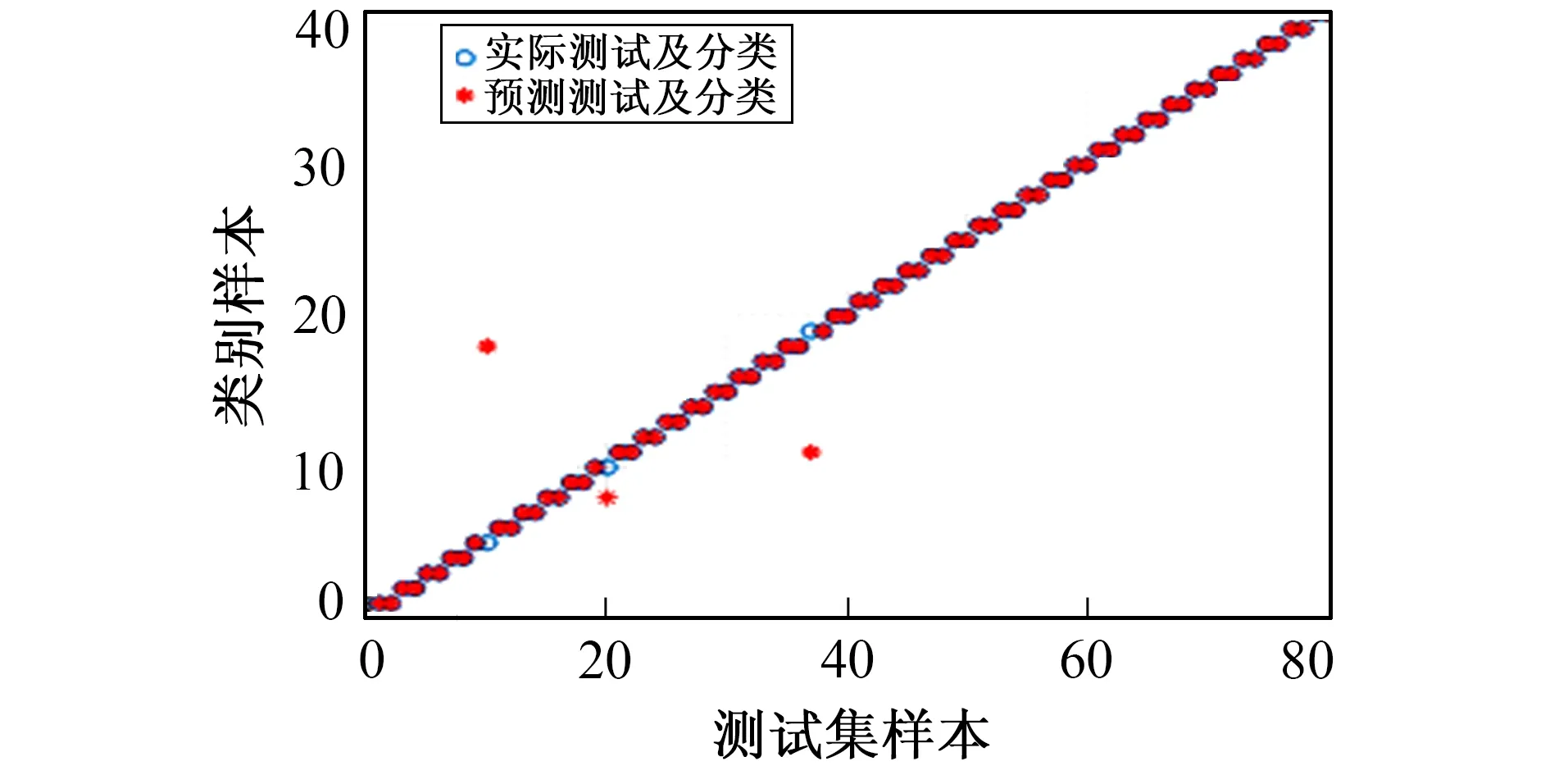
图6 人脸图像测试集的实际分类和预测分类图Fig.6 Face picture classification chart

分别采用由英国剑桥的Olivetti研究实验室创建的ORL人脸库和耶鲁大学创建的Yale人脸数据库验证算法效果。笔者算法(K-CV+PCA+SVM)与其他算法精度比较如表3所示。在ORL人脸库上, 常规的PCA+SVM算法识别准确率是93.5%； 文献[10]采用KICA+SVM算法的准确率为93%； 文献[11]采用Gabor+SVM算法的准确率为88.02%。与这些算法比较, 笔者提出的算法识别精度达到了96.25%, 明显优于其他算法。在YALE人脸库上, 常规的PCA+SVM算法识准确率是81.25%； 文献[10]采用KICA+SVM算法的准确率为83.66%； 文献[11]采用Gabor+SVM算法准确率为88.78%。与这些算法比较, 笔者提出的算法精度略高。

表3 人脸识别算法精度比较

5 结 语

笔者提出利用交叉验证方法同时使用以改进网格搜索方法对SVM参数寻优, 并联合了PCA和SVM的人脸识别算法, 具有较高的准确率,明显优于常规的PCA和SVM联合的算法。运用Matlab进行验证的结果表明, 此算法提高了模型在人脸识别上的精度,减少了SVM最优参数的搜索时间,具有较好的实际使用价值。