铁路站场往返取车作业优化模型及算法

张 岩，李 想，孙文桥，刘启钢，张 明

（1.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081；2.中国铁路南宁局集团有限公司 柳州站，广西 柳州 545007)

0 引言

铁路站场取送车是为了实现货物装卸、车辆检修清洗等目的，从站场股道向作业地点送车和从作业地点取回车辆的作业过程，包括单送、单取、送取结合等多种形式。其中，现场单取作业场景较多，而且多为可按任意顺序挂走的“普通车流”[1-2]。受到车列最大长度限制，取车作业往往需要多次往返。在此情况下，合理安排调车机车(以下简称“调机”)的取车顺序可以提高机车车辆作业效率，加快车辆集结进度，保证车流的准点出发，有利于缩短车辆周转时间[3]。

铁路站场取送车顺序优化问题是一个经典的NP难问题，目前国内相关研究较多。李文权等[4]采用图论和排序论求解树枝形铁路专用线取送车问题。石红国等[5]将铁路取送车问题抽象为哈密尔顿图最短回路问题进行求解。这些算法的计算次数随着存车股道数量的增加呈指数增加，在存车股道数量较多时，很难在规定时间内求得最优解。郭垂江等[6]利用C-W节约改进算法解决动态规划计算量大、耗时长的问题。有部分学者应用蚁群算法、遗传算法等人工智能算法求解取送车计划优化问题，有效缩短求得可接受解的时间[7-10]。但是，这些研究仅考虑取车、送车、调车等作业一次完成的情况，未考虑多次往返目标作业地点的取车场景，算法也难以在有限时间内快速求解。另外，还有一些研究表明[11-14]，蚁群算法可以在有限时间内求解旅行商问题的最优路径，然而多次往返取车模型涉及“城市”访问次数动态变化的情况，传统蚁群算法无法直接求解。为此，考虑车组最大长度和最晚取回目标站场时间限制，将股道入口信号机与车组之间距离、牵出车组长度纳入到调机总走行距离计算公式，建立数学模型以描述铁路站场取车作业过程。改进传统蚁群算法步骤，使其适应城市访问次数动态变化条件下旅行商问题求解，计算得到多次往返取车作业顺序的最优方案。

1 铁路站场往返取车作业优化模型

1.1 问题描述

铁路站场包括到达场、编组场、出发场、车辆检修站场、货物装卸站场等，大多为树枝形站场[8]。树枝形铁路站场布置示意图如图1所示。站场入口处只有1条线路，通过道岔分成多级树枝形线路，最末端线路为作业股道。站场入口和股道入口均设置信号机，调机经入口信号机进入站场，按顺序进入各作业股道连挂车辆组成车列，再经站场入口信号机将车列取回至目标车场。如果车列长度超出最大长度限制，则需要进行多次往返取车，可能需要多次到同一股道取车。铁路站场往返取车作业优化问题可以描述为：以调机总走行距离最短为目标，在完成所有的取车任务的条件下，确定多次往返取车的最优取车顺序。

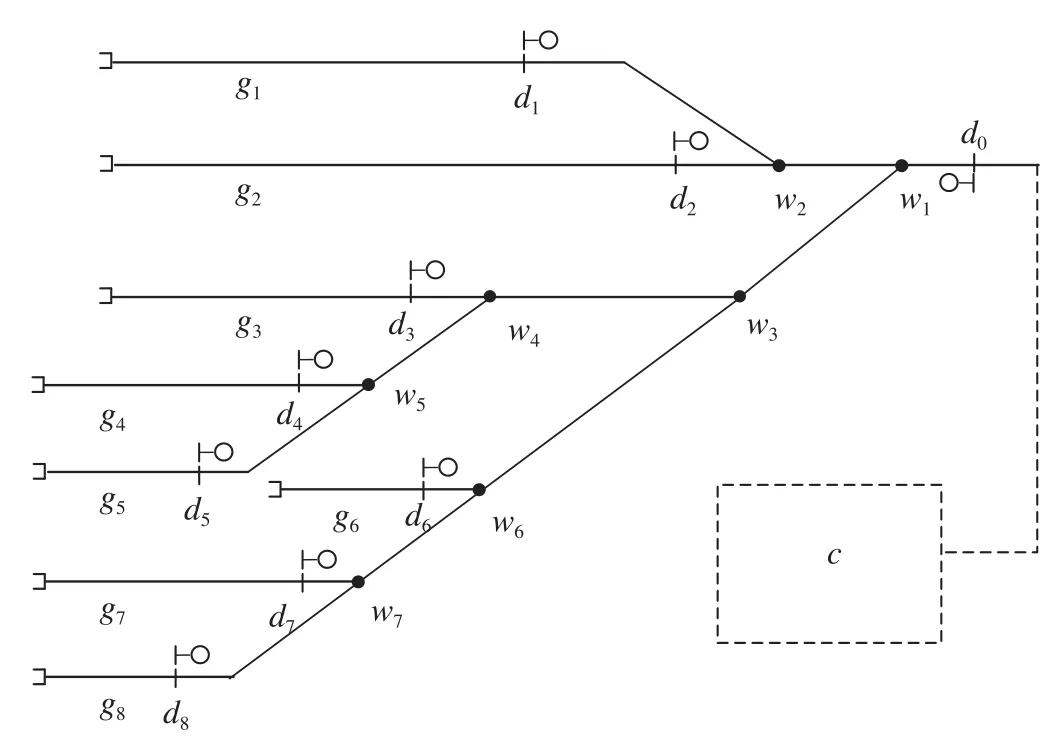
图1 树枝形铁路站场布置示意图Fig.1 Layout of branch-shaped railway yard

为方便建模，提出以下假设：①只采用1台调机进行取车作业，调机的走行平均速度已知；②调机起始位置为站场入口信号机外端；③树枝形站场的线路、道岔、信号机位置已知；④作业开始前，各作业股道停留的车辆数和各车辆长度已知；⑤停留在作业股道上的车组的位置与股道入口信号机的距离已知；⑥车列最大长度限制已知。

1.2 符号说明

设站场有n条作业股道，G= {gi|i= 1，2，…，n}为站场所有作业股道集合。l为车列最大长度限制；d为本站场入口信号机至取车目标站场入口信号机距离；v为调机走行的平均速度。函数d(gi)为本站场入口信号机至作业股道gi入口信号机的距离，函数dg(gi，gj)为作业股道gi的入口信号机经最近折返道岔至作业股道gj的入口信号机的距离。

m为停有待取车组的股道总数，P= {pi|i= 1，2，…，m}为存车股道(在取车开始前有车辆停留的股道)集合。函数d(pi)为本站场入口信号机至存车股道pi入口信号机的距离；函数dlt(pi)为存车股道pi上车组最晚到达目标站场的时间；函数dt(pi)为存车股道pi上车组实际到达目标站场的时间，函数dp(pi)为存车股道pi上车组与该股道入口信号机之间的距离；函数dg(pi，pj)为作业股道pi入口信号机经最近折返道岔至存车股道pj入口信号机的距离。当pi=gi，pj=gj时，有dp(pi) =dp(gi)， 且dg(pi) =dg(gi)，dg(pi，gj) =dg(gi，gj)。函数cn(pi)为股道pi停留车组包含的车辆数；函数ptl(pi)为股道pi停留车组总长度。

Q= (q1，q2，…，qk)为取车股道顺序，其中qi∈P(i= 1，2，…，k)，调机可能到同一存车股道多次取车，因而在取车股道顺序Q中，一个存车股道可能出现多次，有k≥m。函数tl(qi)为在股道qi取走的车组长度，qtl(qi)为连挂股道qi上车组后车列总长度，有qtl(qi) =qtl(qi-1) +tl(qi)。函数ptl(qi)为取完股道qi上车组后，股道qi上剩余车组的长度，有ptl(qi) =ptl(qi) -tl(qi)。调机取车总走行距离为其中dis(qi)为取股道qi上车组的走行距离，表示调机从站场入口信号机外侧或上一次作业结束位置开始，至将目标股道车组牵引至目标股道入口信号机内侧或送至目标站场的走行距离。如果送至目标站场后仍有待取车组，还应包括调机返回站场入口信号机外侧的距离。

1.3 调机走行距离计算公式

给出调机处于不同起始位置时，单次连挂调机走行距离的计算公式。当调机处于站场入口信号机外侧时，连挂后，如果qtl(qi) ＜l，那么

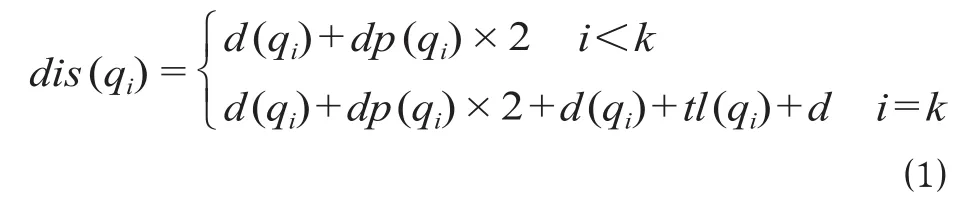
如果dtl(qi) =l，那么

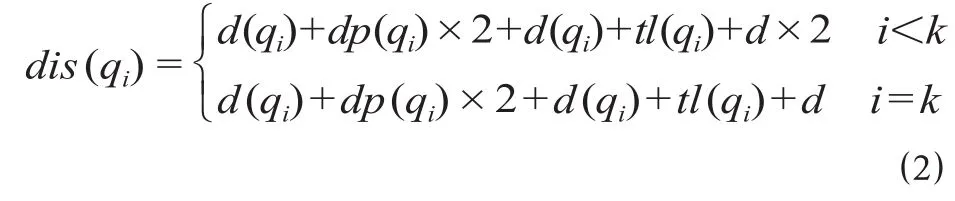
如果qtl(qi) ＞l，那么

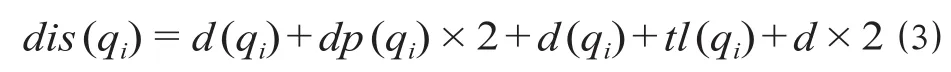
调机取第1个车组之前或送完1个最大长度车列返回时，调机处于站场入口信号机外侧。调机连挂完目标股道车组后，将车组牵出至目标股道入口信号机内侧。公式 ⑴ 表示调机取车组的走行距离包括站场入口信号机至车组所在股道入口信号机的距离、股道车组停留位置距该股道入口信号机距离的2倍。在股道完成一次作业后，将剩余车组与该股道入口信号机之间距离dp(pi)更新为0。当取最后一个车组时，需将车组牵到站场入口信号机外侧并送至目标站场。公式 ⑵ 表示当取完目标股道车组后车列长度达到调机最大牵引推送长度限制时，调机需要额外将车组牵引出站场入口信号机，并往返至取车目标站场，当所有车辆取完时不必返回。公式⑶ 表示当取完目标车组后车列长度大于调机最大牵引推送长度l限制时，调机需额外将车组牵引出站场入口信号机，将车组送至取车目标站场，返回后停留在站场入口信号机外侧。

当调机处于股道时，连挂后，如果qtl(qi) ＜l，那么

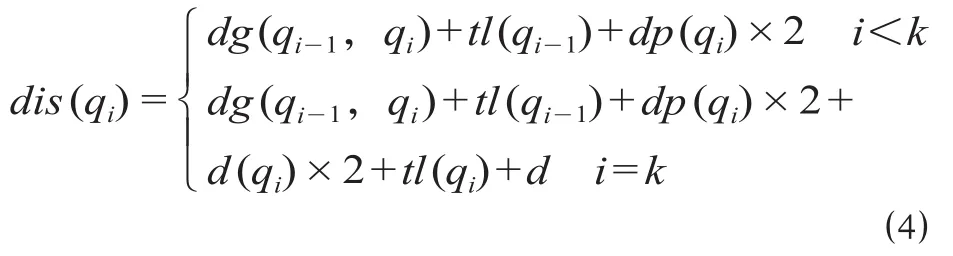
如果qtl(qi) =l，那么

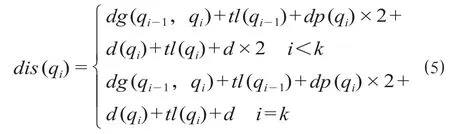
如果qtl(qi) ＞l，那么

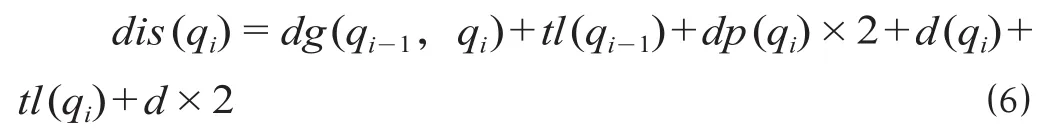
当调机取完某个股道上的车组后，车列长度未达到l且i＜k，调机将股道车组释放在该股道入口信号机内侧，继续取下一个车组。调机需要将上一个股道车组牵出到qi-1至qi的折返道岔外侧，因而调机至下一个股道的走行距离包括股道入口信号机至下一个股道入口信号机之间距离、牵出车组长度和目标连挂车组停留位置距股道入口信号机距离的2倍。公式 ⑷ 至 ⑹ 都包含调机从原股道至取车目标股道的走行距离，公式 ⑷ 表示取最后一个车组时，需要将车组牵出站场入口信号机并送至目标站场。公式 ⑸、⑹ 表示当连挂车组后，车列长度大于等于l时，调机需要额外将车组牵引至站场入口信号机外侧，送至目标站场，返回后停留在站场入口信号机外侧，当作业完毕(即i=k)时不计算返回路程。

对单次连挂调机走行距离的计算公式求和，得到调机总走行距离公式。优化目标是调机将站场所有停留车组取出并送至目标站场的总走行距离R最短，目标函数为

股道上车组到达目标站场的时间dt(pi)为股道上所有车组被送到目标站场时，调机的总走行距离除以调机的平均速度，计算公式为

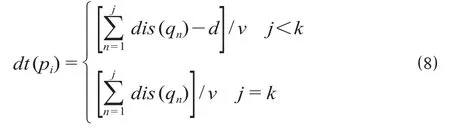
2 铁路站场往返取车作业优化模型求解算法

2.1 求解算法分析

铁路站场取车模型可以抽象为旅行商问题求解。在铁路站场往返取车作业优化问题中，将股道看作旅行商问题中的“城市”，将每次车列的移动看作旅行商问题中“城市”之间的一次“迁移”。当存车股道较少时，可以使用深度优先或广度优先等遍历算法，搜索取车顺序的所有解，从而获得最优解；而当存车股道数量较大时，遍历算法无法在可以接受的时间内完成求解，为此需要借助智能优化算法求解。蚁群算法是解决旅行商问题的一种有效的智能优化算法，可在较短的时间内寻找到NP问题的满意解[10-11]。传统旅行商问题可以描述为：寻找一条距离最短的路径，使旅行商选择1条路径从1个城市出发，经过所有城市1次，再回到出发城市。旅行商问题的实质是在1个带权无向图中找1个权值最小的哈密尔顿回路[12]。但是，传统旅行商问题只能经过同一个城市1次，无法描述多次往返取车的场景。因此，将铁路取车问题抽象成带权有向图的最小权重路径求解问题，节点间弧的权重可动态变化。城市可看作股道，与传统蚁群算法实现不同，城市i可能等于城市j，即调机可以重复经过同一个股道。

2.2 蚂蚁迁移规则

在蚁群算法中，每个蚂蚁根据随机迁移规则选择股道，生成一个完整的取车路径。股道间迁移规则可用公式 ⑼ 描述。

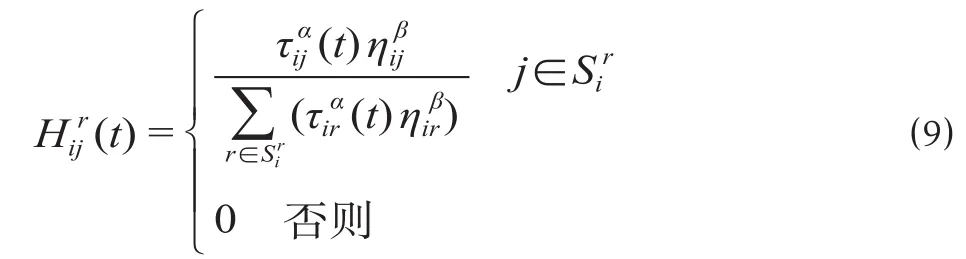
2.3 信息素更新规则

当一次迭代完成，所有蚂蚁都将所有股道上的车组全部取完，并找到一条完整路径后，需要更新路径上的信息素，更新公式为

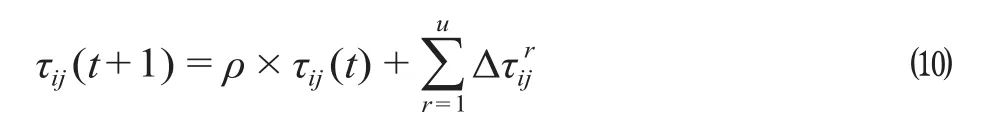
式中：t表示第t次迭代，每次迭代生成全部蚂蚁的路径；ρ为信息素蒸发系数，0 ＜ρ＜ 1 ；τij(t)为第t次迭代节点i到节点j之间路径上的信息素浓度；u表示蚂蚁的数量；表示第r个蚂蚁在弧ij上留下的信息素，其中θ为信息素增加强度系数，当蚂蚁r未经过弧ij时，为0；Disr表示第r个蚂蚁完成全部取车任务的总走行距离。

公式 ⑽ 中，当出现车组实际到达时间超出车组最晚到达时间时，有

式中：DP为晚点惩罚系数。

选取我院不良事件上报系统中2013年1月—2016年12月发生的跌倒坠床事件35例，其中，有陪护23例，无陪护12例；其中，男11例，女24例，年龄56～97岁，其中60岁以下6例，61～69岁有7例，70～79岁有10例，80～89岁有9例，90岁以上3例；08：00 AM—07：59 PM跌倒坠床16人，08：00PM—07：59AM跌倒坠床19人；生活自理能力评分（ADL）均在50～60分之间，其中≤54分12例，≥55分23例；发生在卫生间6例，走廊4例，病室25例。患者自我照顾能力：能自理10人，部分自理16例，不能自理9例。

车组实际到达目标站场的时间算法如图2所示。

图2 车组实际到达目标站场的时间算法Fig.2 Algorithm of arrival time to destination yard of wagon group

2.4 蚁群算法步骤

取车最优路径求解算法函数结构如图3所示。首先，初始化信息素，然后进入循环。每次迭代都先将所有蚂蚁随机放置在股道上，然后循环处理每一个蚂蚁，为其找到完整的取车路径。路径搜索过程与传统蚁群算法不同，传统算法城市数量固定，弧数量固定，可以确定循环次数，通常用For循环实现[11-13]，而取车最优路径问题求解中，每个蚂蚁经过股道的数量可变，因而用图2中第6行所示的While循环实现，循环结束条件是所有股道上车组全部取完。循环处理完所有蚂蚁后，计算并将上一次迭代中的最优路径赋值给第一个蚂蚁。然后，按信息素更新规则更新信息素，进入下一次迭代。当找到满意解或者达到最大迭代次数后，循环结束。

3 算例分析

3.1 基础数据

某编组站树枝形铁路站场线路如图1所示。图1中，g1至g8代表8个股道，d0代表站场入口信号机，d1至d8代表各股道入口信号机，w1至w7为道岔的岔心编号，c为目标站场。调机初始停于d0外侧，车列最大长度限制l= 600 m。假设车辆长度全为均值15 m时，车列最大车辆数量为40。股道入口信号机间距离如表1所示；股道入口信号机与站场入口信号机间距离如表2所示。本站场入口信号机至取车目标站场入口信号机距离d= 2 000 m，调机速度v= 3 m/s。

图3 改进蚁群算法结构Fig.3 Structure of improved ACA

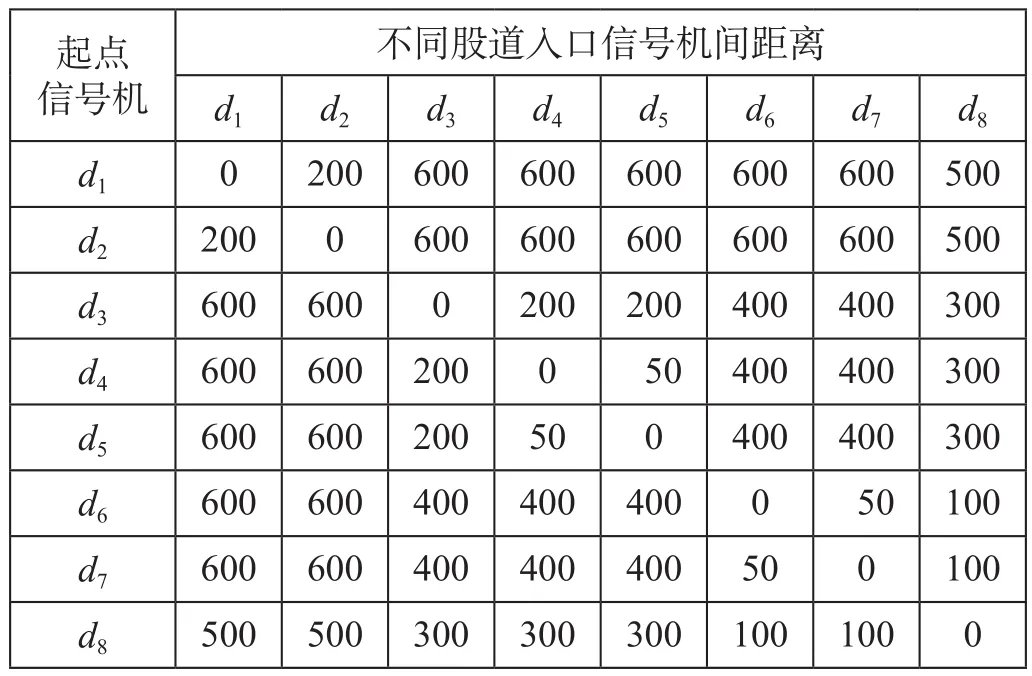
表1 股道入口信号机间距离 mTab.1 Distance between track entrance signals

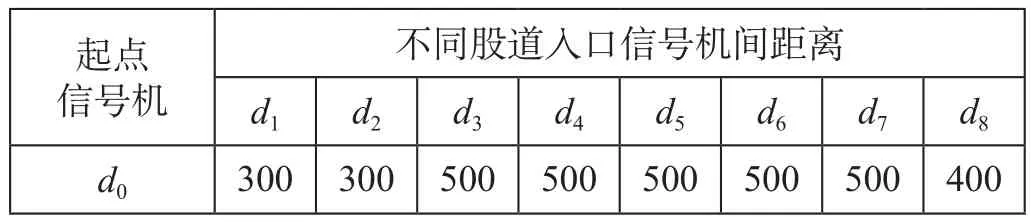
表2 股道入口信号机与站场入口信号机间距离 mTab.2 Distance between track entrance signal and shunting yard entrance signal

3.2 算例结果

当股道g1，g5，g8停有车组时，P= {g1，g5，g8}。车组停放位置描述如表3所示。在一台中央处理器为i7-3630Q 2.4 GHz，内存12 GB的计算机上求解。蚁群算法信息素的重要度α= 0.7，启发因子的重要度β= 0.7，信息素蒸发系数ρ= 0.9，信息素增加强度系数θ= 0.1，最大迭代次数设为1 000，晚点到达惩罚系数DP为20 000 m。蚁群算法迭代10次后可收敛到最优解，求得次优路径为“g8—g5—g1—c—g1—c”，次优走行距离为9 170 m，最优路径为“g1—g8—c—g5—c”，最短走行距离为9 130 m，无晚点，与利用深度优先算法求解得到的结果一致。

表3 车组停放位置描述Tab.3 Description of wagon group parking position

3.3 算法性能分析

为了验证取车最优路径求解蚁群算法执行性能和结果正确性，利用相同站场对不同股道停车情况进行计算，将计算时间和结果与深度优先算法进行对比。车组停放数量描述如表4所示。

表4 车组停放数量描述Tab.4 Description of wagon group parking number

P1至P6代表6种停车情况，如P1代表股道g1，g2，g3上停有车组，6种停车情况具体如下。

P1= {g1，g2，g3}

P2= {g1，g2，g3，g4}

P3= {g1，g2，g3，g4，g5}

P4= {g1，g2，g3，g4，g5，g6}

P5= {g1，g2，g3，g4，g5，g6，g7}

P6= {g1，g2，g3，g4，g5，g6，g7，g8}

针对以上6种停车情况，不考虑最晚到达约束，分别利用深度优先算法和蚁群算法进行求解。蚁群算法相关参数取值为α= 0.7，β= 0.7，ρ= 0.9，θ= 0.1，最大迭代次数设为1 000，不设迭代提前停止条件，晚点到达惩罚系数DP为20 000 m。深度优先算法通过遍历所有路径，求出的最短距离即为最优解。

算例计算结果比较如表5所示。由表5可知，在全部6种停车情况下，蚁群算法求得的最短路径与深度优先算法求得的最短路径相等，即为最优解。随着存车股道数量增加，深度优先算法需要遍历的路径总量和计算时间快速增加，P5和P6的计算时间已经达到92.545 s和3 350.608 s。

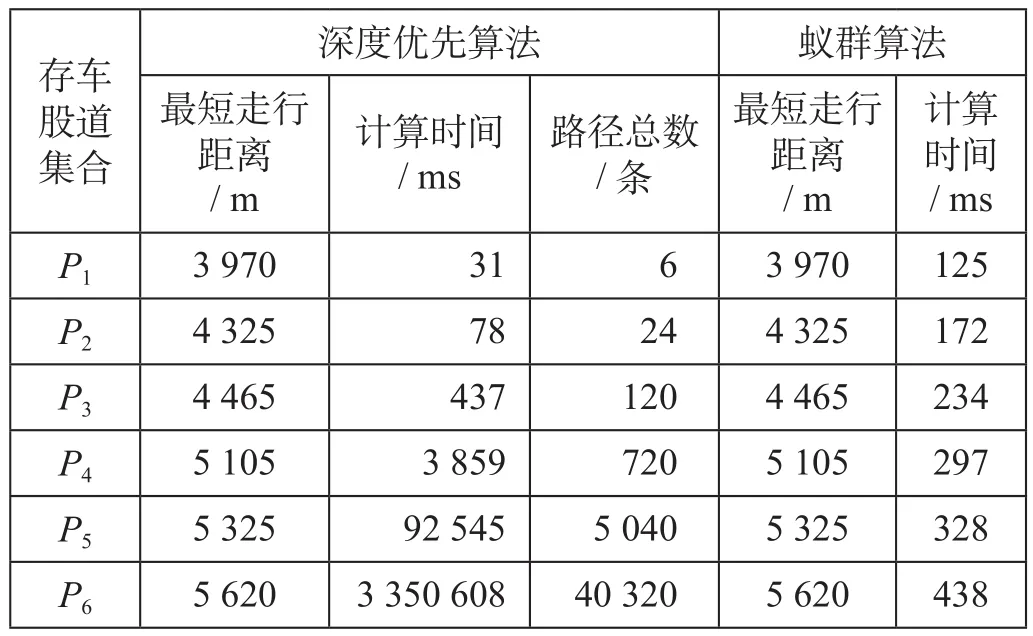
表5 算例计算结果比较Tab.5 Comparison of algorithm case calculation result

算法实际计算时间变化趋势如图4所示。图4的横坐标代表不同存车股道集合，纵坐标代表计算时间，虚线为深度优先算法，实线为蚁群算法。由图4可知，深度优先算法的计算时间随着存车股道数量的增长呈指数增长，蚁群算法计算时间随着存车股道数量的增长呈线性增长，增幅基本不变。在6个股道停车的情况下，蚁群算法计算时间仍小于1 s。

分别对6种停车情况进行100次求解，统计收敛到最优解迭代次数的最小、最大和平均值。不同停车情况下最优解迭代次数统计如表6所示。

由表6可知，每种情况最优解迭代次数的最小值均为1次，最大值随着存车股道数量的增加而不断增加，但均可在100次迭代以后收敛到最优解。实际应用过程中，如将蚁群算法最大迭代次数设为1 000，则可保证大部分情况下在1 s以内求出最优解，计算结果可信，求解算法具备一定的实用性。

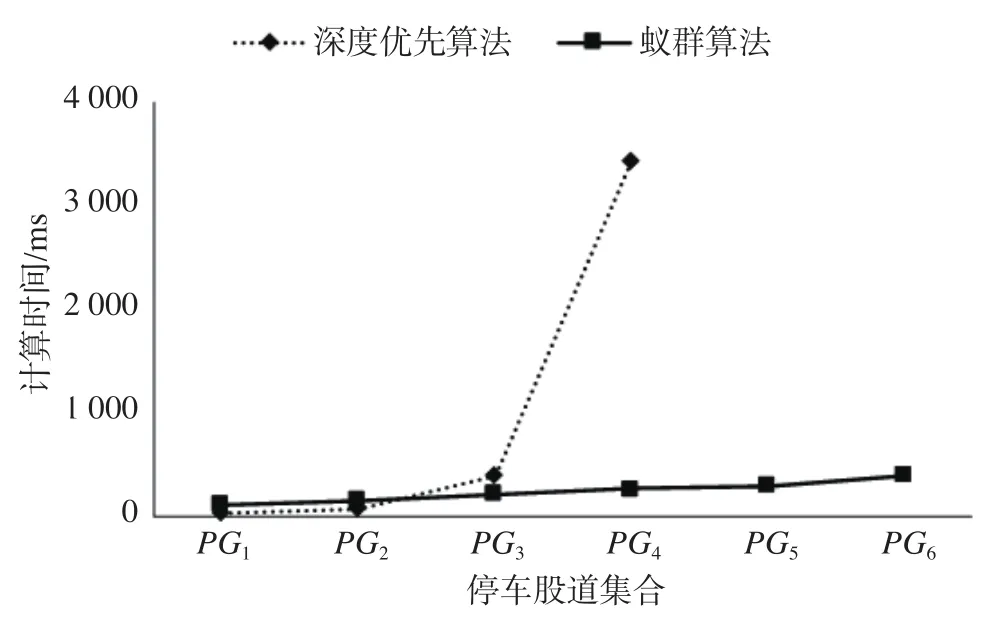
图4 算法实际计算时间变化趋势Fig.4 Variation trend of algorithm actual calculation time

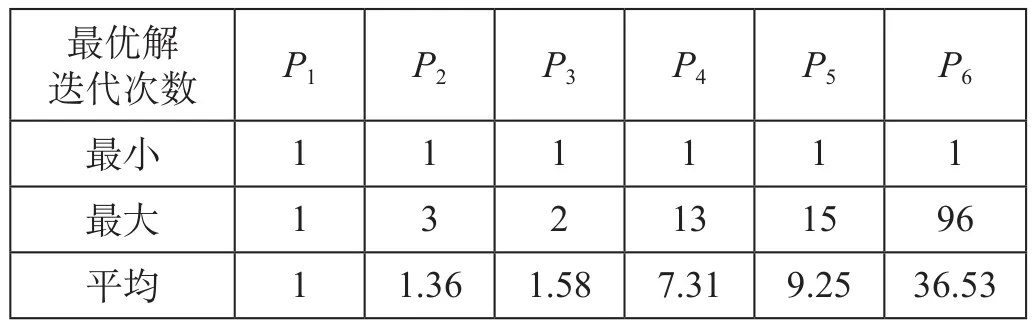
表6 不同停车情况下最优解迭代次数统计 次Tab.6 Statistics of iteration number of different wagon parking situation

4 研究结论

（1）建立铁路站场多次取车作业模型，对实际调车线路参数、牵出车组连挂车数动态变化、调机走行模式等特征进行描述，使模型更接近铁路实际调车作业场景。

（2）当存车股道规模加大，改进蚁群算法较深度优先算法在计算时间上存在明显优势，且实际上都可以在规定迭代次数内获得最优解，能够为铁路站场取车计划编制提供智能辅助决策，有效压缩取车时间，加速车辆周转。