基于离散动态规划的列车节能速度曲线优化
孔繁鑫,陈阳舟,詹璟原,尚 飞
(1.北京工业大学 北京交通工程重点实验室,北京 100124;2.北京工业大学 人工智能与自动化学院,北京 100124)
0 引言
轨道交通以其速度快、运量大、准时安全等特点,成为支撑城市公共交通的重要方式之一[1]。与此同时,城市轨道交通系统的能耗不断增加。据统计,2018年北京市轨道交通系统总电能耗达19亿kW·h,牵引能耗达11亿kW·h,牵引能耗约占系统总电能耗的57.9%[2]。通过优化列车站间速度曲线,可以降低列车的牵引能耗,从而降低轨道交通系统的总能耗。
针对列车站间速度曲线优化问题,国内外学者已经做了大量研究,方法主要分为2类:解析算法和数值算法[3]。最常见的解析算法基于极大值原理,可以找到全局最优解、求解速度快,但不能处理非线性运行阻力和轨道速度限制等复杂的列车实际运行条件[4]。例如,Howlett等[5]利用极大值原理证明了列车最优运行曲线由“最大牵引—巡航—惰行—最大制动”4个阶段组成;Liu等[6]基于极大值原理将最优控制过程分为最大牵引、部分牵引、惰行、部分制动、最大制动5种工况,并找到了各工况的切换点;朱金陵等[7]充分利用线路坡道,用极大值原理求解得到列车优化控制策略。数值算法包括遗传算法、动态规划等。遗传算法存在明显的不足,如迭代参数的确定主要依靠经验、对初始种群依赖性强、搜索速度慢等;动态规划是求解多级决策过程最优化的一种数学方法,常用来处理带约束的优化问题,但其存在“维数灾难”问题。例如,陈荣武等[8]提出基于遗传算法的能耗优化算法,计算了不同运行时分的节能速度曲线;刘炜等[9]提出变长实矩阵编码的多种群遗传算法搜索列车节能运行曲线,增强了寻优过程的稳定性;Ko等[10]利用一阶泰勒公式和梯形规则将最优控制问题转化为多阶段决策过程,动态规划求解得到列车节能速度曲线;Lu等[11]以速度变化量为控制变量,分别用蚁群算法、遗传算法、动态规划3种方法求解速度曲线优化问题,动态规划在离线求解中表现最佳。
既有研究多将整个状态空间作为节能速度曲线优化问题的搜索空间,导致求解的计算量和存储量大,求解时间长。为此,构建以位置为自变量、牵引力/制动力的系数为控制变量的列车节能速度曲线优化模型,根据线路条件将位置离散化,将速度曲线优化问题转换为多阶段决策过程,将状态空间划分成网格状并利用状态空间缩减策略对其缩减,利用离散动态规划求解得到列车站间最优速度曲线和最优控制输入,为列车运行提供参考速度曲线,进而降低列车站间运行的牵引能耗。
1 列车节能速度曲线优化模型构建
在时刻表已知的前提下,列车从某站到下一站存在多条速度曲线满足预定的时间约束。不同的列车速度曲线如图1所示。
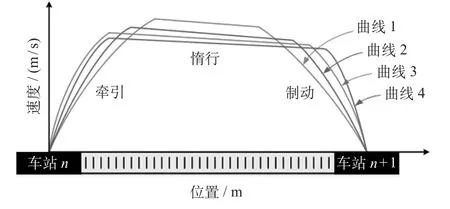
图1 不同的列车运行速度曲线Fig.1 Different speed running profiles of train
列车速度曲线优化就是在固定的站间距离、规定的运行时间下,考虑列车牵引特性、基本阻力、速度限制和坡道阻力等因素的影响,确定一条速度曲线使列车运行过程的牵引能耗最小。将列车视为单质点,以列车位置s为自变量、牵引力/制动力的系数u(u∈[-1,1])为控制变量、速度v和时间t为状态变量,列车节能速度曲线优化模型表示为

式中:J为列车运行过程中的牵引能耗;S为站间距离;f(u,v)为列车牵引力/制动力;f+(u,v)为f(u,v)的正部分;Tra(v),Bra(v)分别为列车最大牵引力和最大制动力,可以从列车的技术手册中获得,也可以通过实验数据拟合得到;M为列车质量;Rb(v)为列车基本阻力,Rb(v) =Av2+Bv+C,参数A,B,C由列车型号、质量等确定[12];Rg(s)为列车坡道阻力,是列车重力在坡道方向的分量,由轨道倾斜程度决定,与列车位置s有关,Rg(s) =Mgsinθ(s) =其中g为重力加速度,g = 9.8 m/s2,θ(s)为轨道倾角,i(s)为轨道每1 000 m的高度差;Vlim为轨道速度限制。
2 离散动态规划算法设计
将位置离散化,使得列车速度曲线优化问题转化为多阶段决策过程,把列车的状态空间离散化为网格状并对其进行缩减,利用离散动态规划对节能速度曲线优化模型进行求解。
2.1 离散化处理
根据线路情况将位置离散化,位置集合由4部分组成:①将站间距离等间隔划分的位置;②限速变化的位置;③轨道坡度变化的位置;④最大速度曲线达到或偏离限速的位置。为了减少不必要的阶段,若等间隔划分的位置离限速变化、坡度变化或最大速度曲线达到或偏离限速的位置小于等间隔位置间距的一半,则删除该等间隔位置,将站间距离S划分为K阶段,产生K+ 1个位置为{s0,s1,…,sk,…,sK}。列车站间运行的有效速度集示意图如图2所示,其中黑色、红色、蓝色、棕色位置分别为等间隔划分、最大速度曲线达到或偏离限速、限速变化和坡度变化的位置。
将控制系数等间隔离散化,可行的控制系数u∈ [-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1],其中负数表示制动,-1为最大制动,0表示惰行,正数表示牵引,1为最大牵引。将列车速度v与运行时间t划分成网格状,每个格子的大小为Δv×Δt。速度和时间的离散间隔会影响最优目标速度曲线的求解精度,理论上,Δv,Δt的取值越小越好。
2.2 状态空间缩减

图2 列车运行有效速度集示意图Fig.2 Schematic diagram of train running effective speed set
为缩小搜索空间,用最大速度曲线与最小速度曲线对速度集合进行缩减。最大速度曲线:在满足轨道限速与终点停车的条件下,列车按照最大牵引力运行。牵引阶段最大牵引力加速至轨道限速,制动阶段从终点倒推,巡航阶段速度与轨道限速相等,没有惰行阶段。最小速度曲线:为按时到达终点,列车在站间有最小速度限制,该限制存在于列车最大速度曲线到达并基本保持在轨道限速的区间,而在该区间外,列车做匀加/减速运动。最大速度曲线与最小速度曲线之间的速度构成了有效的速度集合,即

式中:Vmax,k与Vmin,k分别为最大速度与最小速度曲线sk位置的速度值。
2.3 动态规划正向搜索
列车状态包括列车位置、速度和运行时间,用φ= [s,v,t]表示,初始状态为:φ0= [s0,v0,t0]= [0,0,0]。正向搜索是从初始状态起,由不同的控制输入u搜索满足公式 ⑺ 限制的状态,直到到达终点位置sK。离散动态规划搜索过程如图3所示。图3中的阴影部分对应图2中的有效速度集合,速度落在阴影部分外的为无效控制。
令i,j,p分别为速度、时间、控制的索引,则列车在sk位置的状态表示为在状态的控制表示为
列车第k+ 1阶段的能耗为

列车从s0到sK的总能耗表示为

图3 离散动态规划搜索过程Fig.3 Discrete dynamic programming search process

由贝尔曼最优性原理,公式 ⑴ 的速度曲线优化问题可以转化为多阶段决策问题,具体如下。
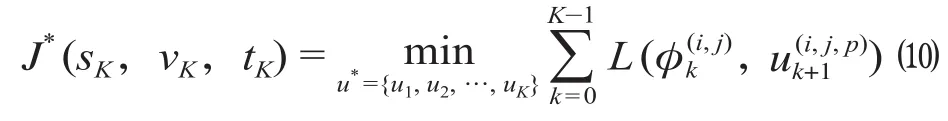
动态规划的递推方程表示为
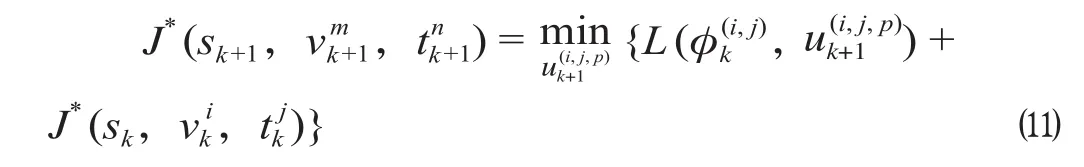
由于位置s是离散的,可选控制输入u也是离散的,正向搜索过程中列车的状态[sk,vk,tk]一般不会落到网格点,将其近似到最近的网格点。需要注意的是,每个状态对应着自初始状态φ0以来的最小能耗。当有多条搜索路径到达同一状态[sk,vk,tk]时,利用公式 ⑾ 选择使得能耗最小的控制作为最优解。
为保存正向搜索结果,构建3个数组:能耗数组、索引数组和控制数组。能耗数组存储列车从初始状态到当前状态总牵引能耗的最小值,索引数组和控制数组存储列车从初始状态到当前状态最优速度曲线对应的上一个状态的索引和控制。
2.4 动态规划反向搜索
反向搜索是根据能耗数组、索引数组和控制数组,利用公式 ⑾ 递推得到列车的最优速度曲线和最优控制输入。反向搜索步骤如下。
步骤1:从终端状态[sK,vK,tK]开始搜索。
步骤2:取当前状态对应的能耗数组、控制数组的值并保存。
步骤3:由索引数组得到当前状态对应的前一状态的索引值并将其作为当前状态。
步骤4:对当前状态进行判断。若当前状态为初始状态,则搜索结束,得到最优速度曲线;否则,转步骤2。
3 仿真验证
为验证算法的有效性,选择北京地铁亦庄线同济南—经海路站间线路,分别对动态规划且状态空间缩减(方案1)、动态规划且状态空间未缩减(方案2)和枚举法(方案3) (与动态规划对状态空间离散化不同,枚举法的速度、时间未离散化处理)进行仿真实验。其站间距离为2 265 m,时刻表规定的站间运行时间为150 s。同济南—经海路轨道坡度和速度限制如表1所示。北京地铁亦庄线列车的牵引特性、制动特性和运行阻力如图4所示。

表1 同济南—经海路轨道坡度和速度限制Tab.1 Track slope and speed limit of Tongjinan-Jinghailu

图4 北京地铁亦庄线列车的牵引特性、制动特性和运行阻力Fig.4 The traction characteristic, braking characteristic and running resistance of trains on Beijing Subway Yizhuang line
将站间位置离散化,方案1和方案2均分为31个阶段,取Δv= 0.1 m/s,Δt= 0.1 s。方案3的计算时间随着阶段数的增加而指数增加,以划分17个阶段为例,搜索对应的站间节能速度曲线。用1.6 GHz处理器、8 GB RAM的个人电脑通过Python编程实现。方案1对应的最优速度曲线和最优控制输入如图5所示。方案3对应的最优速度曲线和最优控制输入如图6所示。方案2求解的节能速度曲线与方案1相同。
北京地铁亦庄线同济南—经海路的节能速度曲线优化3种方案的性能如表2所示。

图5 方案1对应的最优速度曲线和最优控制输入fig.5 The optimal velocity curve and optimal control input corresponding to scheme 1
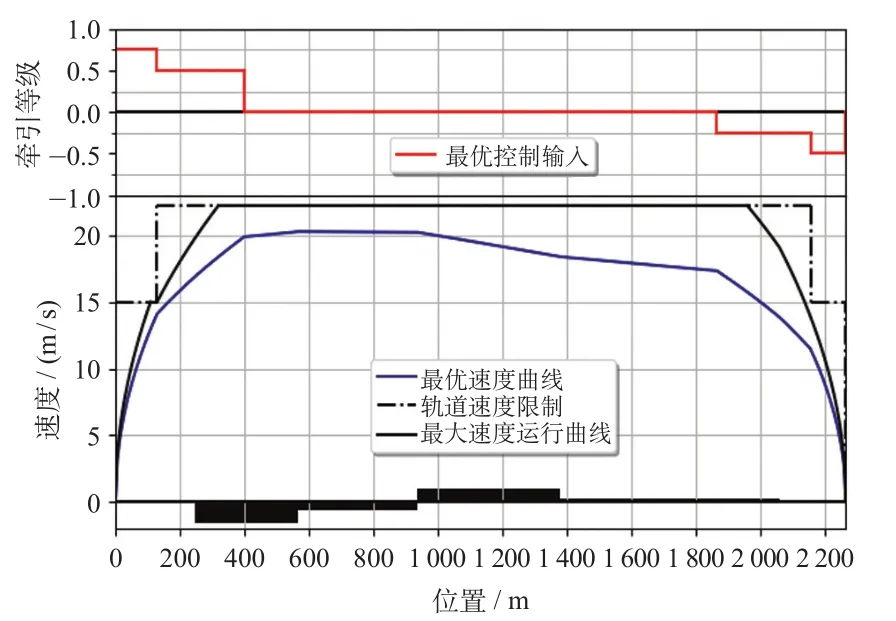
图6 方案3对应的最优速度曲线和最优控制输入fig.6 The optimal velocity curve and optimal control input corresponding to scheme 3
由表2可知,方案1与方案2都采用动态规划方法求解,得到的节能速度曲线相同,终端速度和终端时间的偏差、能耗相同,唯一区别是方案1进行了状态空间缩减,其求解时间仅为方案2的2.5%,状态缩减策略使得搜索效率明显提高。动态规划算法的离散化数据近似处理导致列车终端状态与目标状态产生较大的偏差。方案3采用枚举法求解,速度和时间未进行离散化处理,避免了动态规划状态近似带来的误差,终端状态的偏差较小。但是,方案3计算得到的能耗较大,主要是由于阶段划分较少导致的。然而由于枚举法的计算量、存储量随着阶段数的增加而呈指数趋势增加,如果继续增加阶段数会导致计算机溢出,计算停止。离散动态规划算法解决了枚举法计算量和存储量大的问题,比枚举法减少能耗5.6%,且随着阶段数的增加,得到的节能速度曲线会逐渐逼近全局最优解。可见,动态规划且状态缩减方案可以在较短时间内找到最优的列车站间节能速度曲线。
4 结束语
列车牵引能耗是城市轨道交通系统总能耗的主要部分,优化列车站间速度曲线对降低运营成本、促进低碳经济具有重要的意义。基于离散动态规划求解列车站间速度曲线的优化问题,并利用最大速度曲线、最小速度曲线对状态空间进行缩减,可以提高动态规划算法的搜索效率,降低列车的牵引能耗。仿真实验表明,利用动态规划且状态缩减方案可以在较短时间内找到最优的列车节能速度曲线。为进一步降低城市轨道交通的总电能耗,应考虑多车协作的速度曲线优化问题,利用列车的再生制动能量,减少整个线路列车的牵引能耗。

表2 3种方案的性能Tab.2 Performance of the three scenarios

