LNG罐式集装箱铁路运输维持时间研究
张 辉,吕长乐,翟永涛,李思颖
(1.中国铁道科学研究院集团有限公司 运输及经济研究所,北京 100081;2.中车长江车辆有限公司冷运装备研究所,湖北 武汉 430212;3.武汉奥海辉龙智能测控有限公司,湖北 武汉 430000;4.中国铁道科学研究院 研究生部,北京 100081)
0 引言
液化天然气(LNG)是一种清洁、高效的能源,广泛用作城镇供暖清洁燃料、交通工具用燃料、工业气体燃料及发电燃料等。目前,国内LNG只有管道和公路2种陆上运输方式,LNG铁路运输尚处于空白。作为一种安全、经济、稳定的运输方式,铁路如果参与LNG运输,可以为国家能源结构调整战略提供支撑。考虑铁路运输存在运输时间长、工况复杂的情况,LNG铁路运输的载运工具必须满足铁路运输要求。LNG罐式集装箱(以下简称“LNG罐式箱”)不仅可以实现LNG“一罐到底”的“门对门”运输模式,还可以作为储存、销售工具使用,具有广阔的发展前景[1]。LNG为易燃气体类危险品[2],为确保运输途中不发生BOG(液体介质蒸发产生的低温气体)排放导致的安全风险,必须采用无损储运技术。在LNG罐式箱无损储运技术的指标中,维持时间不仅可以衡量罐式箱的绝热保冷性能,还能够反应其经济性和安全性[3],需要重点研究。
国内外学者通过系统研究LNG储罐分层和翻滚现象,发现外界的漏热量是影响低温储罐维持时间的重要因素[4],良好的绝热性能可以保证罐式箱在储运过程中不发生安全事故[5]。在LNG罐式箱的绝热效果的影响因素中,静态蒸发率是储罐维持时间计算的重要参数,而初始充装率、初始压力、外界环境等因素对维持时间计算结果也会产生影响[6-8]。然而,现有研究大多只研究LNG固定储罐,只有少数研究了海运和公路运输过程LNG罐式箱的维持时间[9-10],而铁路运输过程LNG罐式箱维持时间的相关研究较少。
铁路采用LNG罐式箱运输,其维持时间必须满足铁路长时间、远距离运输的要求,通过构建LNG罐式箱理论维持时间模型,以中车长江车辆有限公司设计生产的1AA型LNG罐式箱(以下简称“中车长江LNG罐式箱”)进行实例分析,验证模型的有效性。采用维持时间模型和维持时间修正模型,分析静态蒸发率、初始充装率、初始压力、运输环境温度等因素对维持时间的影响。
1 LNG罐式箱理论维持时间模型
LNG罐式箱维持时间与罐体绝热性能密切相关,罐体绝热性能越好维持时间越长、安全性越高。静态蒸发率可表征LNG罐式箱绝热性能,是计算LNG罐式箱维持时间的关键参数。在计算LNG罐式箱静态蒸发率的基础上,建立LNG罐式箱维持时间模型,采用维持时间修正模型对计算得到的维持时间进行修正,得到LNG罐式箱理论维持时间。
1.1 LNG罐式箱静态蒸发率模型
静态蒸发率又称为静态日蒸发率,指LNG罐式箱在90%以上额定充满率状态下静置达到热平衡后,24 h内自然蒸发损失的低温液体质量和内容积有效容积下低温液体质量的百分比[11]。LNG罐式箱的漏热量直接影响到静态蒸发率,通常LNG罐式箱的漏热量包括多层绝热体的漏热量和支撑构件的漏热量。
(1)多层绝热体的漏热量计算。LNG罐式箱通常采用高真空多层绝热,但LNG罐式箱与外界仍存在着热量传递,并不能实现完全绝热。高真空多层绝热体的热损失(漏热量)计算公式为

式中:Q绝为通过多层绝热体的漏热量,W;q为多层绝热体的热量密度,取0.8 W/m2;Fm为多层绝热体的平均传热面积,m2。
(2)支撑构件的漏热量计算。支撑构件是LNG罐式箱的重要部件,支撑构件连接内外容器形成一道热桥,通过支撑构件将热量传导至罐内。根据圆筒壁热传导方程,支撑构件的单个支撑面漏热量公式为

式中:Q为单个支撑构件(包括上支撑构件、下支撑构件和滑动构件)的漏热量,W;A为该支撑构件横截面积,m2;λ为该支撑构件材质导热系数,W/(m·K);ΔT为传热温差,K;h为该支撑构件热传导长度,mm。
(3)静态蒸发率计算。LNG罐式箱的静态日蒸发率α计算[12]公式为

式中:Q总为整体漏热量,W;γ为绝对压力为0.1 MPa下LNG的汽化潜热,kJ/kg;V为LNG罐式箱内容积,m3;ρ为LNG密度,kg/m3;φ为充装率,%。
1.2 维持时间模型
考虑初始充满率和液体膨胀对维持时间的影响,假设:①气液达到完全热平衡,即罐式箱内的液体蒸发速度与气相空间的气体冷凝速度相等,气相液相内温度、压力、密度处处相等,漏入的热量全部用于液体表面的蒸发;②液体膨胀导致罐内压力上升,顶起安全阀,即随着漏热的热量不断增加,罐内温度和压力持续上升,最终达到设定的安全阀整定压力时,安全阀的阀芯被顶起,产生起跳动作,从初始状态到安全阀起跳之间的时间即为维持时间[13]。维持时间模型需满足体积守恒方程、质量守恒方程、能量守恒方程3个方程。
体积守恒方程表示初始状态和终了状态体积不变,可以表示为

式中:Vl1,Vg1分别为初始状态液体、气体体积,m3;Vl2,Vg2分别为终了状态液体、气体体积,m3。
质量守恒方程表示初始状态和终了状态质量不变,可以表示为
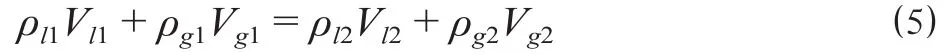
式中:ρl1,ρg1分别为初始状态液体、气体密度,kg/m3;ρl2,ρg2分别为终了状态液体、气体密度,kg/m3。
能量守恒方程表示外界进入的热量等于终了状态和初始状态热力学能之差,可以表示为

式中:Q为累积传热量,kJ;μl1,μg1分别为初始状态液体、气体比热力学能,kJ/kg;μl2,μg2分别为终了状态液体、气体比热力学能,kJ/kg。
日传热量Qd可由静态蒸发率计算获得,可以表示为

式中:m为罐式箱的额定充装量,kg;α为静态蒸发率,%/d;γ为绝对压力为0.1 MPa下LNG的汽化潜热,kJ/kg。
维持时间ts为累积传热量与日传热量之比,可以表示为

1.3 维持时间修正模型
维持时间模型假设罐内气液完全热平衡,外界传入的热量全部用于液体表面的蒸发,并没有考虑由于传热导致的液体热分层现象。由于热分层的存在,LNG罐式箱实际升压速度更快,实际维持时间要小于模型计算结果。考虑初始充满率、压力和漏热量对升压速度的影响,采用修正模型对维持时间模型计算结果进行修正如下[14]。

式中:t'为无因次时间,d;p'为无因次压力,MPa;a为初始充满率,%;φ为无因次漏热流;ts为维持时间模型计算的维持时间,d;t为修正后的维持时间,d;p为安全阀起跳压力,MPa;p0为罐内初始压力,MPa;pcr为临界压力,MPa;α为静态蒸发率;γ为LNG的汽化潜热,kJ/kg;c为初始液体的比热容,kJ/(kg·K);T为初始温度,K。
2 实例分析
以中车长江LNG罐式箱为例,在计算该箱型的静态蒸发率的基础上,采用维持时间模型和维持时间修正模型计算得到该箱型的理论维持时间,分析静态蒸发率、初始充装率、初始压力、运输环境温度等因素对维持时间的影响。
2.1 LNG罐式箱静态蒸发率计算
1AA型LNG罐式箱的漏热量Q总包括多层绝热体的漏热量Q绝和支撑构件的漏热量Q支撑,该箱型Fm= 87.28 m2,由公式 ⑴ 计算多层绝热体的漏热量Q绝= 0.88×7.28 = 69.82 W。该箱型为“8点支撑”结构,包括2个上固定支撑构件、2个下固定支撑构件和4个滑动支撑构件,材质为环氧玻璃钢,其导热系数λ= 0.35 W / (m·K)。上固定支撑构件玻璃钢管受热截面积A上= 0.016 m2,下固定支撑构件玻璃钢管受热截面积A下= 0.024 m2,滑动构件玻璃钢管受热面积为A滑= 0.01 m2,所有玻璃钢管长度均为h= 135 mm,ΔT= 182 K。由公式 ⑵ 可以分别计算出Q上支撑= 15.1 W,Q下支撑= 22.65 W,Q滑动= 18.87 W,机械支撑构件的漏热量Q支撑=Q上支撑+Q下支撑+Q滑动= 56.62 W。除多层绝热体和支撑构件的漏热量之外,还存在进液管、增压管、溢流管等管路的漏热量,由于这些管路受热截面积非常小,整体漏热量可以忽略不计。因此,该箱型整体漏热总量Q总=Q支撑+Q绝= 56.62 + 69.82 =126.44 W。
LNG罐式箱的静态日蒸发率α按公式 ⑶ 计算,其中γ为绝对压力为0.1 MPa下LNG的汽化潜热,查化学化工物性数据手册[15],γ= 511.12 kJ/kg;该箱型内容积V为45 m3;LNG密度ρ取427 kg/m3;充装率φ取90%,计算可得该箱型静态蒸发率α=0.124 %/d。
LNG罐式箱的静态日蒸发率计算结果低于LNG集装箱允许的静态日蒸发率0.18 %/d,因而该计算箱型罐体结构的绝热性能满足要求。该箱型由第三方检测机构检测的静态蒸发率结果为0.12 %/d,与模型计算结果非常接近,证明了该静态蒸发率计算方法的有效性。
2.2 LNG罐式箱理论维持时间计算
采用维持时间模型计算该箱型的维持时间,利用修正模型对计算结果进行修正,得到该箱型的理论维持时间。LNG主要组分为甲烷,因而在计算中,介质用液体甲烷代替LNG。理论维持时间模型计算条件如表1所示;1AA型LNG罐式箱维持时间计算结果如表2所示。表2中的物性参数通过物性软件REFPROP获得,日传热量Qd通过公式 ⑺计算得到,无因次漏热流φ按照公式 ⑼ 计算得到。
由表2计算结果可知,采用维持时间模型计算出的维持时间为165.9 d,修正后维持时间为100.3 d,满足不低于90 d的铁路运输条件要求[16]。从表2还可以看出,随着压力的升高,同样的压力增幅,维持时间的增幅越来越小,如压力从0.1 MPa上升到0.15 MPa需要16.3 d,而从0.55 MPa上升到0.6 MPa只需要6.5 d。

表1 理论维持时间模型计算条件Tab.1 Calculation conditions of theoretical holding time
将理论计算值与第三方检测机构检测的实测值进行对比,据检测报告显示该箱型维持时间实测值为107.4 d。1AA型LNG罐式箱维持时间理论值与实测值对比如图1所示。
理论计算值与实测值相差7.1 d,导致两者存在差别的原因如下:一是初始条件不同,理论维持时间初始压力是0.1 MPa绝对压力,而实测时充液后罐内气液平衡时初始压力接近于0 MPa;二是在理论计算时介质采用的是液体甲烷,而实测中采用的是LNG,其主要组分是甲烷,还存在着少量乙烷和丁烷。实证对比结果表明,该箱型的理论维持时间与实测维持时间比较接近,两者变化趋势基本一致。
2.3 影响因素分析
以中车长江LNG罐式箱为例,采用维持时间模型和维持时间修正模型,分析静态蒸发率、初始充装率、初始压力、运输环境温度(温差)对理论维持时间计算结果的影响。初始计算条件如表3所示,不同影响因素对维持时间计算结果的影响如图2所示。

表2 1AA型LNG罐式箱维持时间计算结果Tab.2 Calculation results of 1AA LNG tank container theoretical holding time

图1 1AA型LNG罐式箱维持时间理论值与实测值对比图Fig.1 Comparison between theoretical and measured holding time of 1AA LNG tank container
由图2计算结果可知:①随着静态蒸发率的增加,维持时间显著减少,当静态蒸发率为0.1 %/d时,维持时间为120.9 d,而当静态蒸发率为0.2 %/d时,维持时间只有57.9 d。因此,在铁路运输时建议采用静态蒸发率低、绝热效果好的LNG罐式箱。②随着初始充装率的增加,维持时间呈现出下降的趋势,初始充装率越大下降幅度越大、维持时间越短。因此,在运输时罐内初始充装率应满足相关规定,严禁超载。③随着初始压力的增加,维持时间大幅度减少。当初始压力为0.1 MPa时,维持时间为100.3 d;当初始压力为0.3 MPa时,维持时间为44.3 d;当初始压力为0.5 MPa时,维持时间只有14.6 d。因此,在铁路运输开始前,罐内初始压力应保持较低水平,以保障运输安全。④运输环境温度越低维持时间越长,当平均环境温度为-20 ℃时,维持时间为129.7 d,当平均环境温度为40 ℃时,维持时间为89.8 d。结论与LNG罐式箱冬季储运时间较长夏天储运时间较短的现象相一致[17]。因此,在开展LNG罐式箱铁路运输时应考虑环境温度的影响,在夏季高温运输时适度缩短运输时间。
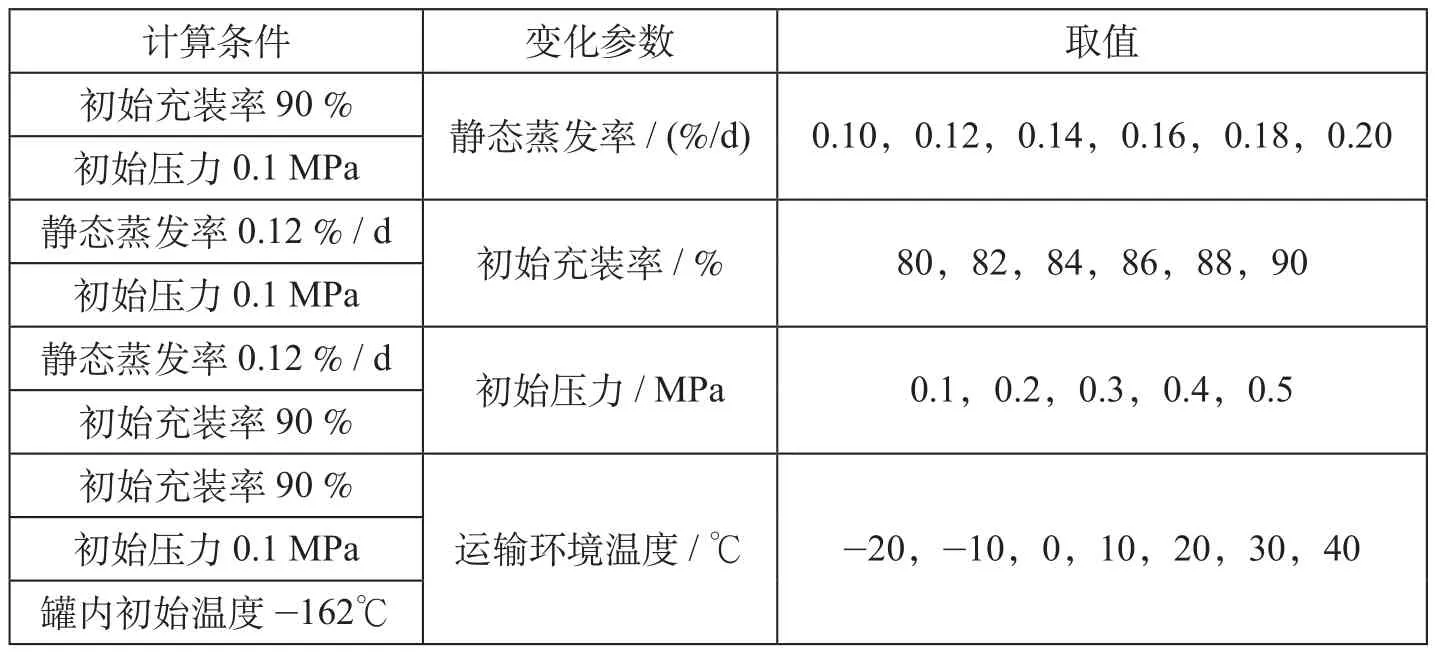
表3 初始计算条件Tab.3 Initial calculation conditions

图2 不同影响因素对维持时间计算结果的影响Fig.2 Influence of different factors on the calculation results of holding time
此外,在运输过程中LNG罐式箱不可避免地会产生各种振动,打破罐内液体分层边界,使不同温度层的液体、气体和液体更充分地混合,使罐内受热趋向于均匀,降低罐内压力,进而延长维持时间。中车长江车辆有限公司通过LNG罐式箱公路运输监测数据验证了该现象,公路运输10 d罐内压力增长0.01 MPa、温度升高2.5 ℃,运输过程中罐内温度、压力的增长速度低于静置状态。因此,LNG罐式箱在运输过程中维持时间有一定程度的增加。
3 结束语
维持时间是LNG罐式箱能否实现铁路长时间远距离运输的重要判别指标。通过构建维持时间模型及维持时间修正模型,准确获得LNG罐式箱铁路运输维持时间,同时充分考虑到运输过程中静态蒸发率、初始充装率、初始压力、运输环境温度等因素对LNG罐式箱铁路运输维持时间的影响,为保障LNG铁路运输安全提供理论基础。由于目前LNG铁路运输尚处空白、无实际运输数据支撑,模型计算得出的维持时间与实际情况可能存在一定的偏差。未来可根据实际铁路运输数据验证和完善维持时间模型,进一步开展铁路运输剩余维持时间预测的相关研究。

