中西扶贫实验的效果之争:辛普森悖论
徐齐利
(江西财经大学,江西 南昌 330013)
一、引言
2019年的诺贝尔经济学奖授予阿比吉特·班纳吉(Abhijit Banerjee)、艾丝特·杜芙若(Esther Duflo)、迈克尔·克雷默(Michael Kremer)三位经济学家,以表彰他们“在减轻全球贫困方面的实验性做法”(1)诺贝尔奖官方推特:“for their experimental approach to alleviating global poverty”。。此次颁奖,在中国学术界和实务界引起一定的争论:在减贫效果方面,到底西方的扶贫政策更有效还是中方的扶贫政策更有效?对于扶贫政策有效性的评估,到底该采用中方的实验性做法(试点推广法[1-2])还是该采用西方的实验性做法(随机对照法[3-6])?
实际上,扶贫政策有效性的评估,分为事前有效性评估和事后有效性评估两个方面(2)事后有效性评估是指:政策或项目正式实施一段时间之后,对该政策或项目的实际效果做鉴定性评估。事前有效性评估是指:政策或项目在正式实施之前,对政策或项目如果落实将会产生的预期效果做预测性评估。。对于扶贫政策的事后有效性,即在扶贫政策正式实施一定时间之后对减贫效果进行评价,中西方的评估结论是一致的,并无分歧:实践表明,中方的扶贫政策比西方的扶贫政策更有效。例如,世界银行的研究数据显示,从1981年到2015年的35年内,中国累计脱贫7.28亿人,世界其他地区累计脱贫1.52亿人(3)资料来源:世界银行http://iresearch.worldbank.org/PovcalNet/povOnDemand.aspx。。
争议的焦点在于事前有效性的评估。在扶贫政策正式实施之前,同样采取实验性做法评估其有效性,然而,中西式评价结论差异巨大:西式实验评价为有效的扶贫政策,中式实验评价的结论可能是有效、也可能是无效;中式实验评价为有效的扶贫政策,西式实验评价的结论可能是有效,也可能是无效,还可能是不确定[7-16]。
既有文献鲜有问津:中西方在扶贫政策事前有效性的评估上为什么会产生分歧?皆是采取实验的方法来检验扶贫政策的事前有效性,中方采取试点推广法,西方采取随机对照法。实验方法的不同,导致有效性的评价标准自然不同,这是产生分歧的源头。从该源头出发,与均衡理论的研究范式相一致,本文在理论上对分歧的定义、分歧的构造性、分歧的存在性、分歧的唯一性依次展开论述,以此揭示中西方关于扶贫政策减贫效果的事前有效性评价产生分歧的内在机理。
第一,分歧的定义。以脱贫率为测度指标,在中式有效性评价标准的数学定义和西式有效性评价标准进行的数学定义基础上,给出中西式有效性评价分歧的数学定义。对于两扶贫政策的减贫效果评价,(1)无分歧,中西式评价结论完全完全一致,要么皆评价为近似等效,要么皆评价为其中一项政策比另一项政策效果更好;(2)弱分歧,中式评价为其中一项政策比另一项政策效果更好,但西式评价中仅有部分被试支持该结论,另一部分被试却反对该结论;(3)强分歧,中西式评价结论完全相反,在统计上表现为辛普森悖论(4)辛普森悖论:分组评价所得结论与汇总评价所得结论完全相反。例如,法学院和商学院在招生时各自都是女生多于男生,但是从两个学院招生的汇总数据看则是男生多于女生。,一方评价出某项政策效果更好,而另一方评价出另一项政策效果更好。
第二,分歧的构造性。在由政策试验前的贫困人数与政策试验后的脱贫人数构成的直角坐标系内,根据中西式评价关系中的向量加法原理,建立一个满足平行四边形法则的数学模型,完全涵盖中西式评价分歧的所有情形。以两扶贫政策的减贫效果评价为例,其完备性体现在:(1)无分歧有3种情形、(2)弱分歧有4种情形、(3)强分歧有2种情形,合计共有9种情形。
第三,分歧的存在性。(1)以中西式皆评价为近似等效作为基准情形,证明得:若基准情形存在,则在基准情形落点的附近,其他所有情形也肯定存在。(2)对于两扶贫政策的减贫效果评价,在由政策实施前的贫困人数与政策实施后的脱贫人数构成的直角坐标系内,很容易就能找到一例满足中西式皆评价为近似等效这类点的组合。
第四,分歧的唯一性。通过寻找中西式皆评价为近似等效这一基准情形存在的充分且必要条件知:中西式评价为近似等效的基准情形不仅非唯一,而且有无穷多个,几乎可以散落在由政策实施前的贫困人数与政策实施后的脱贫人数构成的直角坐标系第一象限的任何位置。这就是中西方在扶贫政策的减贫效果评价方面,无分歧的各种情形随处可见的同时,弱分歧的各种情形也随时可遇,甚至出现辛普森悖论的强分歧之各类情形也随时不可避免的原因和机理。
该研究的学术贡献:揭示了中式实验性做法与西式实验性做法用于扶贫政策事前有效性评估时结论经常出现分歧的内在机理。该研究的实践启示:(1)中西方因实验方法不同,在扶贫政策事前有效性的评估上结论出现分歧在所难免;(2)因为扶贫归根到底是要贫困人口脱贫,为调和结论上的分歧而对中西方评估的脱贫率再来一道加权求和的数据处理工序,只是为了在量化上不再显示冲突,对实际甄别最有效的扶贫政策几乎毫无裨益;(3)实验性评估扶贫政策的有效性若刻意遵循西式的随机对照法,将会因需要考虑的因素过多,即“维数灾难”,而引发“分组灾难”,最终形成“诊断灾难”,即组间结论相互冲突,对政策效果无法形成确定性的判断;(4)与西式随机对照法遵循因果系统(causal system)的思维方式进行政策实验不同,中式的试点推广法遵循模糊系统(fuzzy system)的思维方式进行政策实验,仅对输入输出进行综合推断的操作能够有效避免“维数灾难”“分组灾难”“诊断灾难”;(5)考虑到辛普森悖论的可调和性与事后评价结论的一致性,对扶贫政策事前有效性的评估若要采取实验性做法,则以中式的试点推广法为主、西式的随机对照法为辅的试验策略较为稳妥。
二、分歧的定义
(一)定义
对扶贫政策的有效性采取实验性的做法进行评估时,西式遵循因果系统(causal system)的思维方式,首先对被试对象按照个体差异性进行分组处理,然后对输入输出进行分组评估,以此甄别何种扶贫政策更有效;中式遵循模糊系统(fuzzy system)的思维方式,不对被试对象按照个体差异性进行分组处理,仅对输入输出进行综合评估,以此甄别何种扶贫政策更有效。中西思维方式不同,导致实验方法的选取不同;实验方法不同,导致有效性的评价标准自然也不同;评价标准不同,导致评价的结论也难以完全相同。这是中西方通过实验性做法评估扶贫政策的有效性时产生分歧的源头。基于上述思想,对中西式有效性的评价标准,以及由此产生的分歧在逻辑上给出严肃的数学定义。
定义1,中式有效性的评价标准:
(1)政策T比政策T'高效当且仅当实施政策T后的脱贫率大于实施政策T'后的脱贫率,即
T≻T'⟺P(H|T)>P(H|T')
(2)政策T比政策T'低效当且仅当实施政策T后的脱贫率小于实施政策T'后的脱贫率,即
TT'⟺P(H|T) (3)政策T与政策T'近似等效当且仅当实施政策T后的脱贫率与实施政策T'后的脱贫率相等,即 T~T'⟺P(H|T)=P(H|T') 定义2,西式有效性的评价标准: (1)政策T比政策T'高效是指不仅在C类人群中实施政策T后的脱贫率大于实施政策T'后的脱贫率,而且在C'类人群中亦是如此,即 (2)政策T比政策T'低效是指不仅在C类人群中实施政策T后的脱贫率小于实施政策T'后的脱贫率,而且在C'类人群中亦是如此,即 (3)政策T与政策T'近似等效是指不仅在C类人群中实施政策T后的脱贫率与实施政策T'后的脱贫率相等,而且在C'类人群中亦是如此,即 (4)政策T与政策T'效果孰高孰低不确定是指,要么在C类人群中实施政策T后的脱贫率比实施政策T'后的脱贫率更高,但在C'类人群中的表现正相反;要么在C'类人群中实施政策T后的脱贫率比实施政策T'后的脱贫率更高,但在C类人群中的表现正相反,即 定义3,中西有效性的评价分歧: (1)无分歧,对于政策T和政策T',从脱贫率上看,中式和西式皆评价为近似等效,或皆评价为T比T'高效,或皆评价为T比T'低效,即 (2)弱分歧,对于政策T和政策T',从脱贫率上看,中式评价为T比T'高效,而西式评价为不确定;或者中式评价为T比T'低效,而西式评价为不确定,即 (3)强分歧,即出现辛普森悖论,对于政策T和政策T',从事后的脱贫率上看,中式评价为T比T'高效,而西式评价为T比T'低效;或者中式评价为T比T'低效,而西式评价为T比T'高效,即 由扶贫前的贫困人数、扶贫后的脱贫人数计算得来的脱贫率知:根据定义1,Case1、Case2、Case3、Case4中式评价政策T比T'更高效;Case5、Case6、Case7、Case8中式评价政策T比T'更高效。根据定义2,Case1、Case8西式评价政策T比T'更高效;Case4、Case5西式评价政策T'比T更高效;Case2、Case3、Case6、Case7西式评价政策T与T'谁更高效不确定。根据定义3,Case1、Case5中西式评价无分歧;Case2、Case3、Case6、Case7中西式评价弱分歧;Case4、Case8中西式评价强分歧,即出现辛普森悖论。具体如下: 在由政策试验前的贫困人数x为横轴,政策试验后的脱贫人数y为纵轴,所构直角坐标系的第一象限内,设点CT、CT'、C'T、C'T'、T、T'的坐标分别为(xCT,yCT)、(xCT',yCT')、(xC'T,yC'T)、(xC'T',yC'T')、(xT,yT)、(xT',yT')。根据平行四边形法则,有如下关系式成立: (xT,yT)=(xCT+xC'T,yCT+yC'T),(xT',yT')=(xCT'+xC'T',yCT'+yC'T') 如果中西式皆评价为T与T'近似等效,则点CT=(xCT,yCT)与点CT'=(xCT',yCT')处在从原点出发的同一条射线上,点C'T=(xC'T,yC'T)与点C'T'=(xC'T',yC'T')处在从原点出发的又一条射线上,点T=(xT,yT)与点T'=(xT',yT')处于从原点出发、且夹在刚才两条射线之间的一条射线上;即CT=(xCT,yCT)、CT'=(xCT',yCT')、C'T=(xC'T,yC'T)、C'T'=(xC'T',yC'T')、T=(xT,yT)、T'=(xT',yT')在第一象限的落点有如下关系式成立: 对于Case1,C:T≻T'要求从原点出发过点CT=(xCT,yCT)的射线在从原点出发过点CT'=(xCT',yCT')的射线的上方,C':T≻T'要求从原点出发过点C'T=(xC'T,yC'T)的射线在从原点出发过点C'T'=(xC'T',yC'T')的射线的上方,C∪C':T≻T'要求从原点出发过点T=(xT,yT)的射线在从原点出发过点T'=(xT',yT')的射线的上方;即这六个点在第一象限形成2个平行四边形。同理,亦可得点CT,CT',C'T,C'T',T,T'处于分别情形Case2、Case3、Case4、Case5、Case6、Case7、Case8时的2个平行四边形及其数量关系。数量关系具体如下: 为书写的方便,记x1=P(H|CT),x2=P(H|C'T),x3=P(H|CT'),x4=P(H|C'T'),d1=P(CT|T∪T'),d2=P(C'T|T∪T'),d3=P(CT'|T∪T'),d4=P(C'T'|T∪T'),其中占比向量(d1,d2,d3,d4)处在如下的单纯形之中: 根据中西式评价的关系,即中西式脱贫率的全概率公式 对上一节分歧构造性做等价变换得分歧函数F(x,d):[0,1]4×∑(4)?R3为 其中, 如果中西式皆评价为T与T'近似等效,则分歧函数F(x,d)的三个分量皆等于0,即 同理,中西式评价的上述8种情形在分歧函数F(x,d)的取值方向依次如下: 其中,Case0、Case1、Case5中的点(x(0),d(0))、(x(1),d(1))、(x(5),d(5))就是中西评价无分歧的地方;Case2、Case3、Case6、Case7中的点(x(2),d(2))、(x(3),d(3))、(x(6),d(6))、(x(7),d(7))就是中西评价弱分歧的地方;Case4和Case8中的点(x(4),d(4))、(x(8),d(8))就是中西评价强分歧的地方,即出现辛普森悖论的地方。 对于分歧函数F(x,d),问题的关键是:点(x(0),d(0))、(x(1),d(1))、(x(2),d(2))、(x(3),d(3))、(x(4),d(4))、(x(5),d(5))、(x(6),d(6))、(x(7),d(7))、(x(8),d(8))是否都存在?直接回答该问题比较困难,可以将其分解为两个递进式的子问题来依次回答。问题1:点(x(0),d(0))是否存在?问题2:若点(x(0),d(0))存在,那么点(x(1),d(1))、(x(2),d(2))、(x(3),d(3))、(x(4),d(4))、(x(5),d(5))、(x(6),d(6))、(x(7),d(7))、(x(8),d(8))是否也存在? 首先回答问题2:若点(x(0),d(0))存在,那么点(x(1),d(1))、(x(2),d(2))、(x(3),d(3))、(x(4),d(4))、(x(5),d(5))、(x(6),d(6))、(x(7),d(7))、(x(8),d(8))是否也存在? 定理:对于连续可微的分歧函数F(x,d):[0,1]4×∑(4)⟺R3,有F(x(0),d(0))=0成立。DF(x(0),d(0))表示该分歧函数F(x,d)在点(x(0),d(0))处的(4+3)×3雅各比矩阵。若DF(x(0),d(0))(y):R4+3?R3是一个满射函数(5)满射函数的定义:如果对于Rm中的每一个b,Rn中至少存在一个x使得F(x)=b成立,则称函数F:Rn?Rm为满射函数。,则F(x,d)在点(x(0),d(0))处是一个局部满射函数(6)局部满射函数的定义:设x0为函数F:Rn?Rm定义域中的一个点,有F(x0)=b0;如果对于Rn中以x0为中心的任意开球Br(x0),在Rm中存在一个以b0为中心的球Bs(b0),使得对于Bs(b0)中任意的b,在Br(x0)中至少存在一个x满足F(x)=b,则称函数F在点x0处是一个局部满射函数。,从而点(x(1),d(1))、(x(2),d(2))、(x(3),d(3))、(x(4),d(4))、(x(5),d(5))、(x(6),d(6))、(x(7),d(7))、(x(8),d(8))在点(x(0),d(0))附近自然也存在。 证明:DF(x(0),d(0))(y):R4+3?R3是一个满射函数,这就意味着,对于任意向量b=(b1,b2,b3)T,方程组DF(x(0),d(0))(y)=b都是有解的。根据线性方程组解的存在性定理(7)线性方程组解的存在性定理:由m×n的矩阵A组成的线性方程组Ax=b,对任意的向量b=(b1,…,bm)T,未知数x=(x1,…,xn)T都有解的充分且必要条件是:系数矩阵A的秩rank(A)等于方程的个数m,且未知数的个数n不少于方程的个数m,即:n≥m=rank(A)?Ax=b有解。,因系数矩阵DF(x(0),d(0))的行数小于列数,故线性方程组DF(x(0),d(0))(y)=b有解的充要条件是系数矩阵的秩等于系数矩阵的行数,即rank(DF(x(0),d(0)))=3。既然系数矩阵的秩rank(DF(x(0),d(0)))=3,则在矩阵DF(x(0),d(0))中一定存在一个3×3的子矩阵是非奇异的。为标记的方便,不妨设左边的3×3子矩阵 非奇异。对此,可以将x1,x2,x3看作是函数F的内生变量,x4,d1,d2,d3为外生变量。 基于分歧函数F(x,d):[0,1]4×∑(4)?R3,定义新函数G(x,d,b):[0,1]4×∑(4)×R3?R3,即 其中x1,x2,x3是内生变量,x4,d1,d2,d3,b1,b2,b3是外生变量。由F(x(0),d(0))=0知函数G(x,d,b)在点(x(0),d(0),0)处的值G(x(0),d(0),0)=0,即 根据隐函数定理(8)隐函数定理:该脚注过长,读者可联系作者获得详细说明。知,对于中心点(x4,d1,d2,d3,b1,b2,b3)=(x(0)4,d(0)1,d(0)2,d(0)3,0,0,0)邻域内的点(x(1)4,d(1)1,d(1)2,d(1)3,b(1)1,b(1)2,b(1)3),b(1)1,b(1)2,b(1)3>0,存在点(x(1)1,x(1)2,x(1)3)使得 成立。这就是说,在点(x(0),d(0))=(x(0)1,x(0)2,x(0)3,x(0)4,d(0)1,d(0)2,d(0)3)的附近存在点(x(1),d(1))=(x(1)1,x(1)2,x(1)3,x(1)4,d(1)1,d(1)2,d(1)3)使得 F1(x(1)1,x(1)2,x(1)3,x(1)4,d(1)1,d(1)2,d(1)3)=b(1)1>0 F2(x(1)1,x(1)2,x(1)3,x(1)4,d(1)1,d(1)2,d(1)3)=b(1)2>0 F3(x(1)1,x(1)2,x(1)3,x(1)4,d(1)1,d(1)2,d(1)3)=b(1)3>0 Case1成立。同理可证得,在点(x(0),d(0))附近亦存在点(x(2),d(2))、(x(3),d(3))、(x(4),d(4))、(x(5),d(5))、(x(6),d(6))、(x(7),d(7))、(x(8),d(8))依次使得Case2、Case3、Case4、Case5、Case6、Case7、Case8成立。证毕。 然后回答问题1:点(x(0),d(0))是否存在?由分歧函数F在点(x(0),d(0))处的雅各比矩阵DF(x(0),d(0)),即 其中 知,只要x3≠x4,雅各比矩阵DF的秩就等于3。 在x3≠x4的条件下,若能找到使F(x,d)=0的点即为Case0的点(x(0),d(0))。令x1=x3=0.70,x2=x4=0.45,d1=d3=d3=0.25,则F(x,d)=0。这就是说,在点(x(0),d(0))=(x(0)1,x(0)2,x(0)3,x(0)4,d(0)1,d(0)2,d(0)3)=(0.70,0.45,0.70,0.45,0.25,0.25,0.25)处,F(x(0),d(0))=0,rank(DF(x(0),d(0)))=3,即点(x(0),d(0))存在。从而分歧的存在性完整得证。 寻找问题1基准情形Case0的点(x(0),d(0))存在的充分且必要条件 知,点(x(0),d(0))有无穷多个;再由对问题2的回答知,Case2、Case3、Case4、Case5、Case6、Case7、Case8的点(x(1),d(1))、(x(2),d(2))、(x(3),d(3))、(x(4),d(4))、(x(5),d(5))、(x(6),d(6))、(x(7),d(7))、(x(8),d(8))也有无穷多个。点(x(0),d(0))不仅非唯一,而且大量存在,几乎可以散落在由政策试验前的贫困人数与政策试验后的脱贫人数构成的直角坐标系第一象限的任何位置,这就是中西方在扶贫效果的评价方面,无分歧(x(0),d(0))、(x(1),d(1))、(x(5),d(5))大量存在的同时,弱分歧(x(2),d(2))、(x(3),d(3))、(x(6),d(6))、(x(7),d(7))也大量存在,甚至出现辛普森悖论的强分歧(x(4),d(4))、(x(8),d(8))也大量存在的内在机理。 与政策事后有效性的评估方法(处理效应模型,如倍差法DID、倾向得分匹配PSM、断点回归RD)不同,政策事前有效性的评估一般采取模拟法或实验法。通常首选实验法,只有在不具备做实验的条件下,方才选择模拟法。而且,在政策可实验的条件下,选择田野实验比实验室实验更能准确评估政策的事前有效性。在扶贫政策事前有效性评估的方面,当首选田野实验的做法是中西方学术界和实务界的共识。当前的分歧在于当采取何种田野实验方能准确评估扶贫政策的事前有效性,这是中西方的实务界尤为关心之处,也是中西方的学术界绝不可回避之处。因此,上述理论研究,站在学术界的视角,对中式的试点推广法、西式的随机对照法在扶贫政策事前有效性的评价中产生的分歧进行了机理分析。 下面站在实务界的视角,由上述理论分析得出的实践启示可概括为:对扶贫政策事前有效性的评估若要采取实验性做法,则以中式的试点推广法为主、西式的随机对照法为辅的试验策略较为稳妥。理论分析之所以能够得出这一实践建议,是因为采取实验性做法评估扶贫政策的事前有效性时,在实验设计和操作上不得不基于如下考虑: (1)中西方因实验方法不同,在扶贫政策事前有效性的评估上结论出现分歧在所难免;(2)因为扶贫归根到底是要贫困人口脱贫,为调和结论上的分歧而对中西方评估的脱贫率再来一道加权求和的数据处理工序,只是为了在量化上不再显示冲突,对实际甄别最有效的扶贫政策几乎毫无裨益;(3)实验性评估扶贫政策的有效性若刻意遵循西式的随机对照法,将会因需要考虑的因素过多,即“维数灾难”,而引发“分组灾难”,最终形成“诊断灾难”,即组间结论相互冲突,对政策效果难以形成确定性的判断(9)为尽量得到较为明确的结论,西式采取的补救式做法通常是:在试验结束后的数据分析阶段,采取倾向得分匹配(PSM)、分位数处理效应模型等统计、计量方法来识别前期的实验效果。;(4)与西式随机对照法遵循因果系统(causal system)的思维方式进行政策实验不同,中式的试点推广法遵循模糊系统(fuzzy system)的思维方式进行政策实验,仅对输入输出进行综合推断的操作能够有效避免“维数灾难”“分组灾难”“诊断灾难”。 以2019年度诺贝尔奖经济学奖授予“在减轻全球贫困方面的实验性做法”为契机,以此次颁奖在中国扶贫领域的学术界和实务界引起争论为背景,针对中式的试点推广法和西式的随机对照法,理论研究:中西方在扶贫政策事前有效性的实验评估上为什么会产生分歧?在研究方法上与均衡理论的研究范式(均衡的定义→均衡的构造性→均衡的存在性→均衡的唯一性→均衡的稳定性)相一致,对分歧的定义→分歧的构造性→分歧的存在性→分歧的唯一性依次展开理论阐述。 研究发现:(1)以脱贫率为测度指标,由中西式有效性的评价标准及其分歧的数学定义知中西方的分歧在程度上有三个等级,无分歧、弱分歧、强分歧。(2)在由政策试验前的贫困人数与政策试验后的脱贫人数构成的直角坐标系内,根据中西式评价关系中的平行四边形原理建立的数学模型能够完全涵盖中西式评价三个分歧等级中的所有情形。(3)以中西式皆评价为近似等效作为基准情形,证明得,若基准情形存在,则在基准情形落点的附近,其他所有情形也肯定存在。(4)由基准情形存在的充分且必要条件知,基准情形不仅非唯一,而且有无穷多个,几乎可以散落在直角坐标系第一象限的任何位置。 给定逻辑前提:中西思维方式不同→实验方法的选取不同→有效性的评价标准自然也不同→评价的结论也难以完全相同;本理论研究揭示了:中式实验性做法与西式实验性做法用于扶贫政策事前有效性评估时结论经常出现分歧的内在机理。结合实验的设计难度和操作难度,本理论得出的实践启示为:对扶贫政策事前有效性的评估若要采取实验性做法,则以中式的试点推广法为主、西式的随机对照法为辅的试验策略较为稳妥。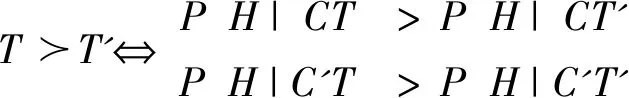
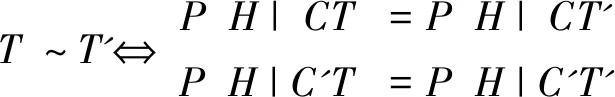
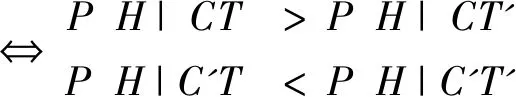
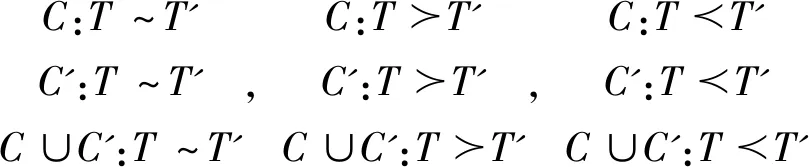
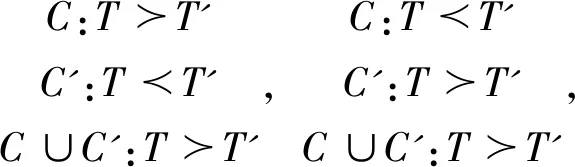
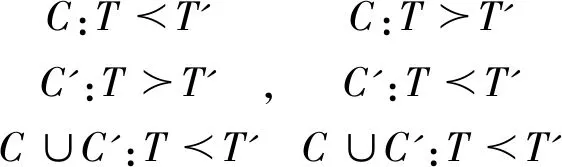
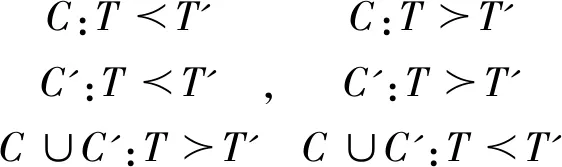
(二)示例
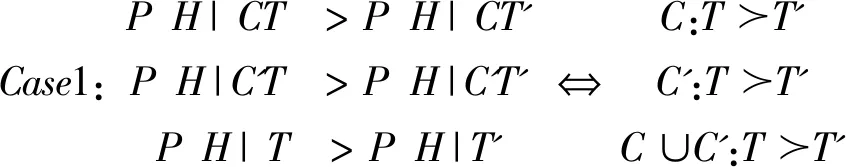
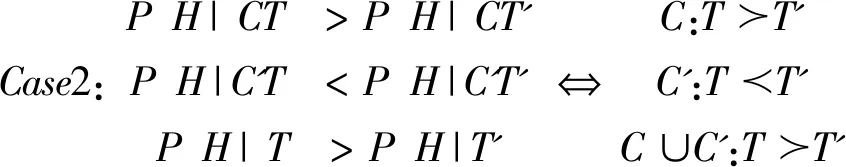
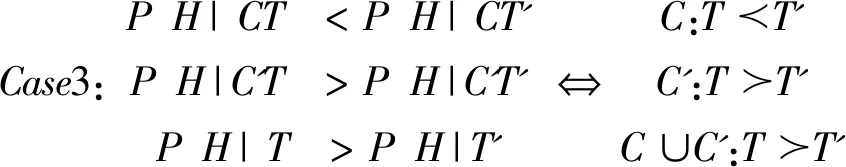
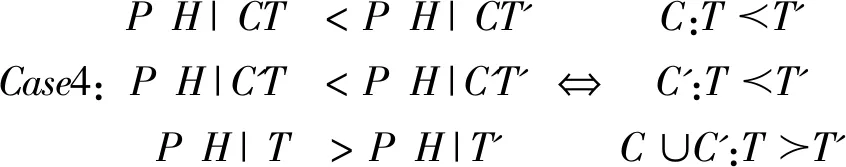
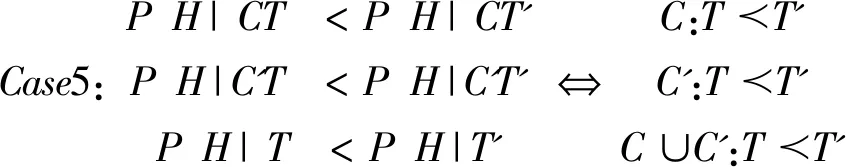
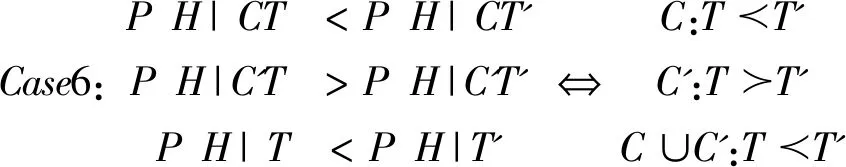
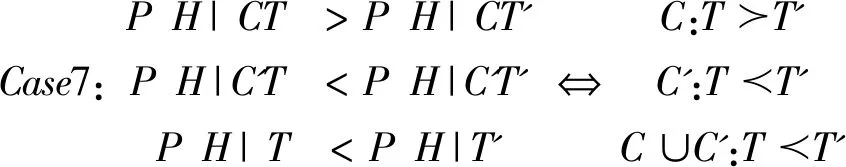
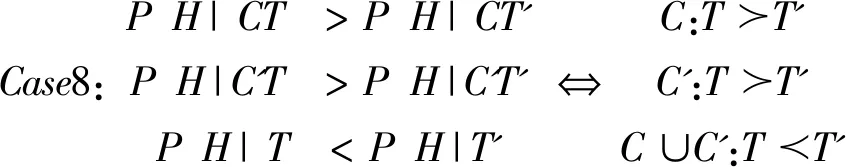
三、分歧的构造性
(一)构造
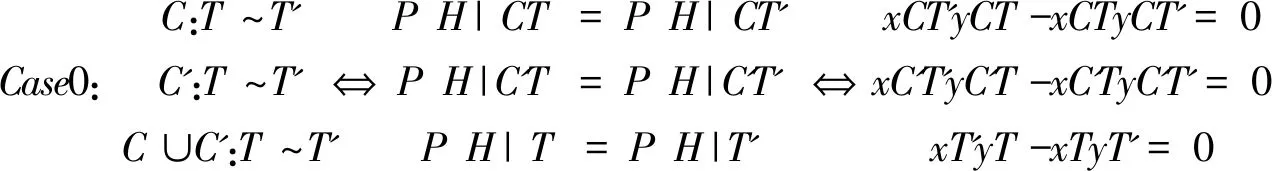
(二)示例
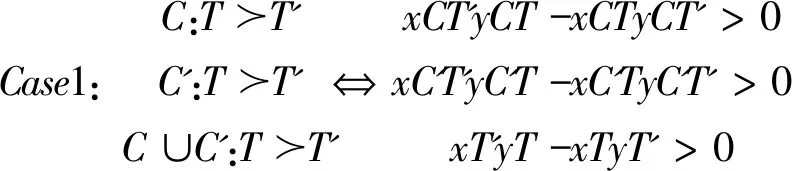
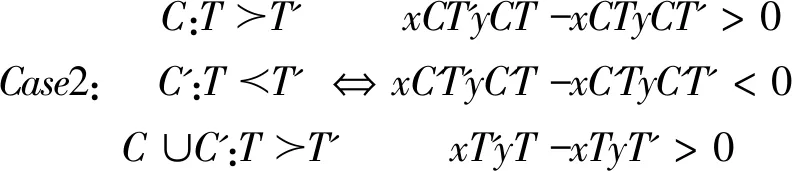
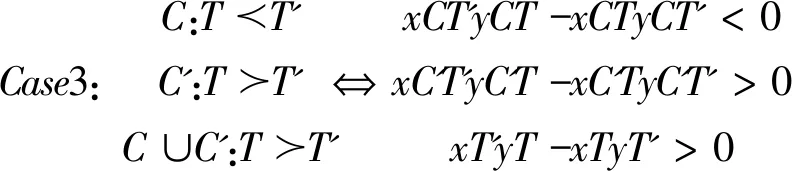
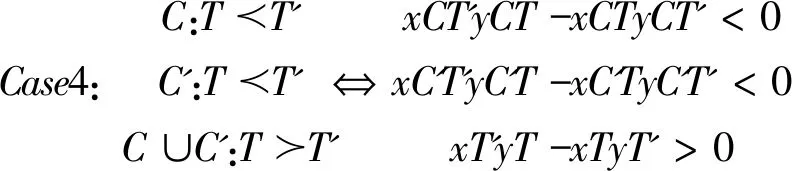
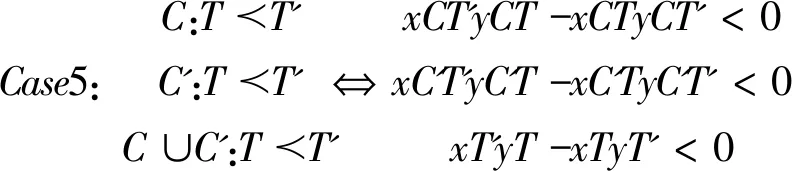
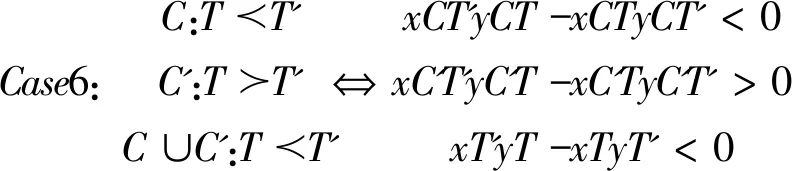
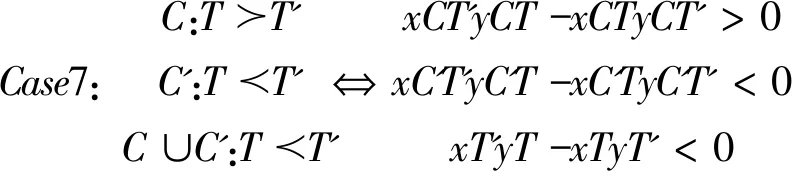
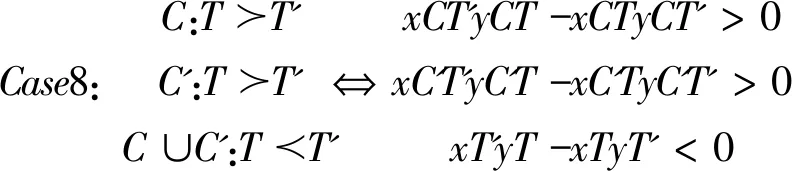
四、分歧的存在性
(一)函数
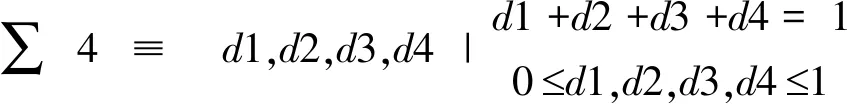
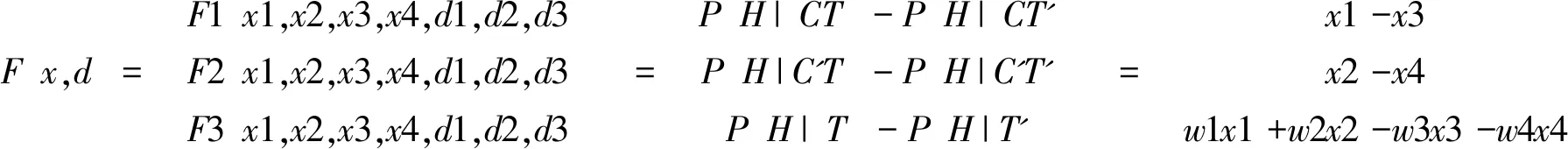
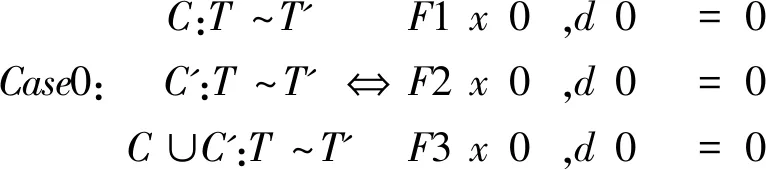
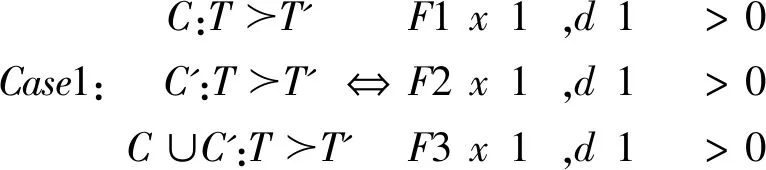
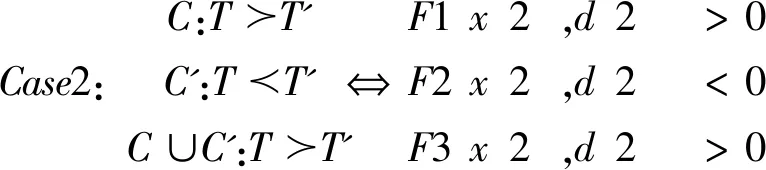
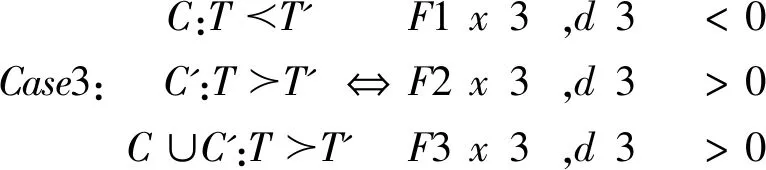
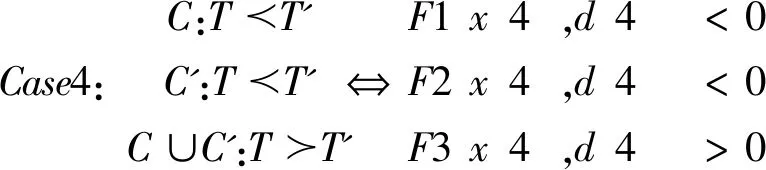

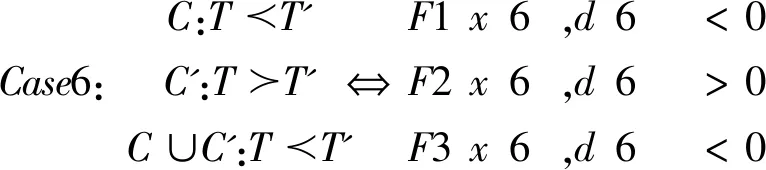
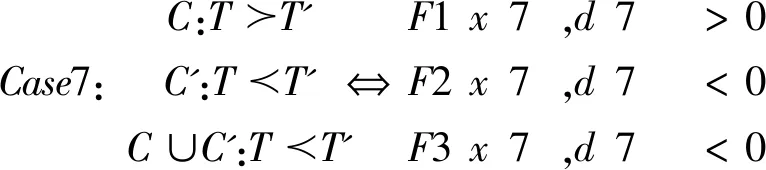
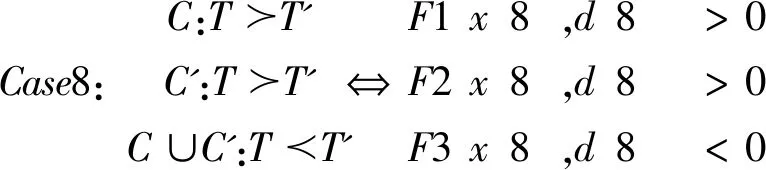
(二)定理
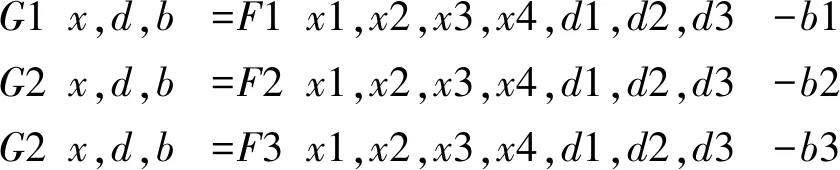
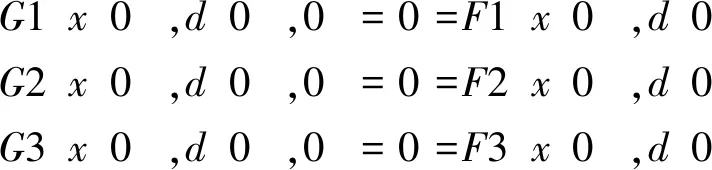
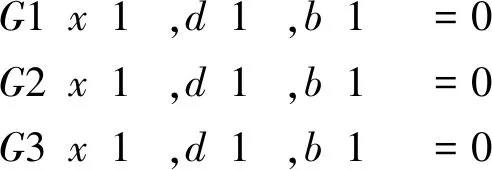
(三)示例
五、分歧的唯一性
(一)条件
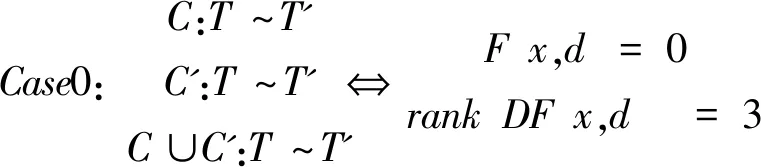
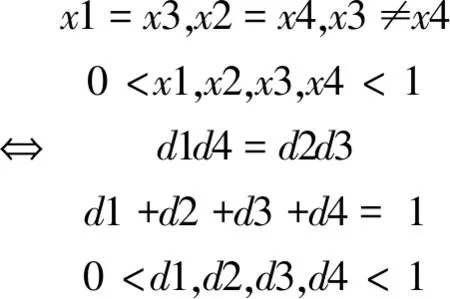
(二)反思
六、结论

