胶合木T 梁负弯曲性能试验研究

饶真宇，王解军，宁 凡

（中南林业科技大学，湖南 长沙 410004）

“绿色，健康，环保”已成为当今世界发展的主题，胶合木作为绿色建筑材料是顺应发展潮流的合理选择[1]。传统木结构由于木节、斜纹等缺陷引起应力集中，导致木材强度无法充分发挥，现代木结构建筑采用胶合木取代原木，弥补了古代木结构在跨径、承载和功能方面的不足；同时，随着我国旅游业发展、自然环境与传统建筑保护的需求及产业政策支持，现代木结构建筑将得到大力研究和推广应用。

关于木材材料力学性能，Frangi 等[2]提出了双线性理想弹塑性拉压本构关系模型，此模型将受压区上升段假定为线弹性，当荷载达到抗压屈服强度后应力保持不变，但该模型忽略了进入塑性阶段后受压区的应力应变变化的情况。Blass 等[3]基于大量试验提出了能真实反映木材拉压的应力应变关系，但是该模型参数较多，计算分析较为复杂。1980 年 Bazan 等[4]简化了 Blass 模型，提出了线弹性的Bazan 模型，该模型将受压区上升段和下降段均视为线弹性，与实际情况符合较好。1981年Neuhaus[5]考虑木材的各向异性特征，以含水量为参数通过拉伸和扭转试验研究了云杉的弹性行为，但对于塑性阶段尚未分析。1990 年Buchanan[6]研究了木材的弯曲强度与轴向拉伸和压缩强度之间的关系，建立了拉压与弯曲强度之间关系的模型，但是并未考虑材料的各向异性特征。2012 年Melzerová 等[7]就单板厚度对层压单板木材抗弯强度的影响进行了研究，发现使用成熟木单板的弯曲强度较幼木单板提高7%～22%。

关于木梁构件，1994 年Rammer 等[8]研究了剪切强度和梁的尺寸及剪切强度和弯曲强度之间的关系，提出了胶合木矩形梁抗剪强度经验公式，但是该公式对于尺寸较大的结构并不适用。2018年曹磊等[9]整理了前人的研究成果并分析了剪跨比、构件尺寸、测试方法、裂纹及干湿条件对胶合木梁抗剪性能的影响，评价了胶合木梁抗剪设计的几种理论方法，但是并未给出确切的承载能力计算公式。同年，胡小锋[10]对胶合木梁受火后的炭化速度、力学性能和耐火极限进行了研究，并通过有限元模拟得到了耐火极限随持荷比、截面尺寸的变化规律，但是忽略了木材的各向异性特征，需进一步研究高温下木材顺纹、横纹方向上的材性。2019 年杨涛等[11]试验研究了胶合木T梁的正弯曲承载力，探明了其弯剪破坏特征及承载力计算方法，但是基于试件个数较少，结论可靠性有待提高。

关于胶合木梁性能增强及组合构件，至今许多学者开展研究取得了大量成果。2007 年杨会峰等[12]研究了FRP 对胶合木梁受弯性能的影响，得到与常用构件相比FRP 会增强梁刚度和受弯承载力分别达到1.35 倍和1.82 倍这一结论，并提出受拉面层破坏荷载和极限荷载的计算公式，但是对于其他截面形式梁并未涉及研究。许清风等[13]、杨昕卉等[14]分别于2012 年和2017 年研究了钢板胶合木梁，发现通过在梁底部黏贴钢板或增设螺钉的方式可提高构件的变形能力和受弯承载力，随钢板厚度的增加，承载力先增大后减小，但没有详细地分析层间剪切对胶合木梁抗弯性能的影响。2017 年郭楠等[15]在胶合木受拉区底部粘贴胶合竹板，通过试验研究发现粘贴的竹板层数在1 ～3 层时梁的极限荷载提高了16.8%～45.9%，之后随层数增加其承载能力下降，并提出对应的受弯承载力计算公式，但是该公式仅针对于传统矩形截面梁，对于不同截面形式梁并不适用。同年，张冰等[16]研究了木—混凝土组合梁，发现在木混组合结构中梁的抗弯刚度随剪力连接程度的提高而增大，但是对剪力连接螺钉与木梁间的连接性能并未进行研究。2019年张晋等[17]在胶合木梁体内布置贴合受弯构件弯矩图形状的抛物线形预应力筋，对比直线布筋发现曲线布筋对梁的抗弯极限承载力和抗弯刚度的提升幅度更大，但是并没有给出胶合木梁在增强后的极限承载能力计算模型。

本研究将首先介绍构件的材料属性、设计尺寸、加载装置、测量方案；然后描述构件的破坏形态和破坏机理，详细分析了荷载挠度曲线、荷载应变曲线和翼缘板正应变横向分布曲线以及极限承载能力；最后总结全文，给出相关结论，并对亟待解决的问题进行进一步讨论。

1 材料与方法

1.1 构件材料与设计

制备2 组共6 根兴安落叶松平行胶合木T 梁，采用聚氨酯结构胶，T 梁由翼板和肋板胶合形成。A 组试件（3 根）尺寸为250 cm×25 cm×21 cm（长×宽×高），高跨比为1/11，剪跨比为5.24，其中翼板由2 块3 cm 厚、肋板由5 块3 cm 厚木板胶合而成（图1）；B 组试件尺寸为250 cm×25 cm×18 cm（长×宽×高），高跨比1/14，剪跨比6.11，其中翼板由2 块3 cm 厚、肋板由4 块3 cm 厚的木板胶合而成（图2）；两组试件仅肋板的高度不同。为避免发生局部承压破坏，在支座及跨中承压处加设横隔板。兴安落叶松物理力学性能由材性实验测得，聚氨酯结构胶物理力学性能由南京天竹科技实业有限公司提供（表1）。

表1 材料物理力学性能Table 1 Physical and mechanical properties of materials

图1 A 组试件横截面Fig. 1 Cross section diagram of 1-3 specimens

图2 B 组试件横截面Fig. 2 Cross section diagram of 4-6 specimens

1.2 加载与测量方案

加载布置如图3 所示。为模拟连续T 梁跨中支座处的负弯矩及支反力，将T 梁试件反转成倒T 梁，两端为铰支座，在跨中施加单点集中荷载。跨中顶部放置厚5 cm 的钢板，钢板上设置100 t压力传感器；在梁端支座处、L/2 及跨中位置共布置5 个百分表（图3a）；每个试件跨中截面沿高度方向布置6 层正应变测点，第1 ～5 层每层布置2 个测点（左、右侧表面各1 个），第6 层布置5 个测点（位于梁底表面），共15 个正应变测点，测点编号见图3b-c。试验全程由荷载控制，采用分级加载方式，主要测试在试验全过程中试件的下挠、截面弯曲应变变化与极限承载力，使用TST3826 静态应变测试系统采集数据。

2 结果与分析

2.1 破坏形态与机理分析

2 组试件破坏模式均是在倒T 梁截面中部肋板处发生顺纹剪切破坏（图4）。初始加载时倒T 梁处于弹性工作阶段，挠度增加平缓。当荷载增大至极限荷载的65%或以上时，木纤维受压屈曲，随着一声清脆声响，梁内部开裂。随荷载的增加，肋板表面形成与梁纵轴线之间夹角很小的斜裂缝。当达到最终破坏荷载时，肋板中部出现较长的纵向水平裂缝，并延伸至梁端，木梁跨中挠度急剧增加，发生顺纹剪切破坏，属于脆性破坏。

《美国木结构规范ASTM D198》[18]指出：对于胶合木梁受弯时，当剪跨比小于2.5，一般产生剪切破坏；当剪跨比大于2.5 且小于6 时，剪切及弯曲破坏均可能发生；当剪跨比大于6 时，一般产生弯曲破坏。本次试件的剪跨比，A 组为5.24、B 组为6.11，两组试件均发生剪切破坏，与美国规范的结论稍有区别。

机理分析。由试验可知，两组胶合木倒T 梁的破坏形态均是顺纹剪切破坏。因为木材顺纹方向抗拉强度大而抗剪强度小（抗拉＞抗弯＞抗压＞抗剪），且试验梁高跨比较小、剪跨比较大，随荷载增加，中性轴附近剪应力率先达到抗剪屈服强度，试件跨中肋板位置发生顺纹错动并发出低沉开裂声响，裂缝由此开展。随着荷载持续增加，由于木材顺纹抗压能力弱于顺纹抗拉能力，肋板顶端位置的木纤维失稳起皱率先受压屈服，中性轴下移，最大剪应力位置同时下移，裂缝急剧开展并延伸至梁端，试件破坏。剪切主裂缝位于梁中性轴下方，并与纵轴线之间夹角很小，裂缝曲线较平（图4g）。

一个课堂的精彩在于看到这些去回应，重新让这些断裂的点连续起来，形成一种内在的节奏和旋律。这种节奏和旋律是一种和谐的声音。如果没有这些矛盾，也就没有和谐的声音，只是一些平淡、索然无味、形式上看似和谐的东西。但只有所有的矛盾和冲突背后的张力，才能凸显出和谐的美，就像我们看到光是因为有黑暗一样。

2.2 荷载-挠度曲线

两组试件的荷载-跨中挠度曲线及力学性能分别见图5 和表2 ～3。

由图5知，试件在加载过程中经历了弹性阶段、弹塑性阶段直至到塑性破坏阶段。因为木材为塑性材料，无明显物理流线，根据Banzan 等[4]所提出木材双线性拉压本构关系把受压区开始进入塑性阶段定义为屈服点，在对比两组试件的荷载-跨中挠度曲线发现：A 组试件在达到0.67Pu前曲线呈线性增长，之后随着荷载的增加抗弯刚度逐渐降低，挠度增量逐渐变大，试件进入弹塑性阶段直至破坏；B 组试件在达到0.7Pu前具有弹性性质，随着荷载增加，塑性性质表现越来越明显，直至破坏。

对比表2 中两组试件抗弯性能数据发现，B组与A 组试件相比，屈服荷载降低9.7%，屈服位移提高27.5%，极限承载力降低10.4%，极限位移提高42.7%，延性系数提高22.4%，表明随剪跨比增大，构件的极限承载力降低，但延性系数提高。取各试件0 ～0.4Pu时的割线刚度为试件初始抗弯刚度，各试件初始弯曲刚度对比如图6 所示，可知A 组试件的初始抗弯刚度大于B 组试件。

2.3 荷载-应变曲线

每组试件跨中截面沿高度方向每一层测点的正应变平均值随荷载的变化曲线如图7 所示，其中测点1 代表第1 层测点，余同；每组试件的测点平均应变沿截面高度方向的分布如图8 所示，其中竖轴代表跨中截面的高度，横轴代表测点的平均应变；图8 中的正、负号分别表示受拉和受压。

图4 胶合木倒T 梁破坏形态Fig 4 Glued wood inverted T beam failure form

图5 荷载-跨中挠度曲线Fig 5 Load - midspan deflection curve

由图7 ～8 可知，在加载过程中弹性阶段跨中截面的应变符合平截面假定，1 ～4 号应变测点处于受压区，应变为负；5 号应变测点处于受拉区，应变为正。从加载初期至试件破坏，各应变测点的数值先随荷载的增大而线性增大，当加载超过屈服荷载后，木材的拉、压应变与荷载变化表现出非线性关系，试件进入塑性阶段。对比A、B 两组试件的荷载-应变曲线图发现：受压区先进入塑性阶段，受拉区后进入塑性阶段，说明兴安落叶松木材的顺纹抗拉屈服强度高于顺纹抗压屈服强度，最终破坏时抗拉性能并未充分发挥。

2.4 跨中截面翼板正应变的横向分布

在每个试件跨中截面翼板底面均匀布置5 个正应变（纵向应变）测点，取每组试件测点应变的平均值，每级荷载对应下的翼板正应变横向分布如图9 所示。由图9 可知，翼板正应变的横向分布不均匀，呈现中部大、两端小分布，具有对称性，并且随荷载增大应变分布不均匀性愈加突出；在最大荷载等级（54 kN）下，两组试件翼板应变横向分布的不均匀性基本相同，翼板中心位置的应变比两端大30%，这是由于梁的弯曲剪力滞所致。

表2 构件力学性能试验数据Table 2 Mechanical properties test data of components

表3 两组试件试验数据对照Table 3 Comparison of test data of two sets of test pieces

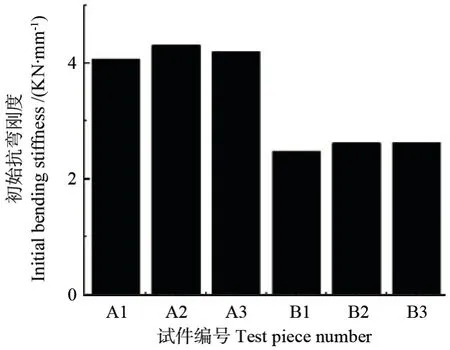
图6 初始抗弯刚度Fig. 6 Initial flexural stiffness

2.5 承载能力极限状态分析

本次试验的两组试件均发生顺纹剪切破坏，所以只对剪切破坏强度进行理论分析。

图7 荷载-应变曲线Fig. 7 Load- Strain Curve

图8 应变沿截面高度方向的分布Figure. 8 Distribution of strain along the height of the section

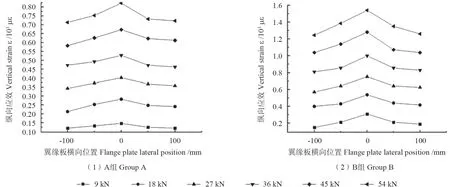
图9 翼板正应变的横向分布Fig. 9 Lateral distribution of normal strain of flange plate

胶合木倒T 梁在试验荷载作用下，其跨中截面中心轴位置的最大剪应力，可按如下公式计算：

式（1）中：τ0为试验荷载下胶合木倒T 梁跨中截面中心轴位置的剪应力（N/mm2）；V为试验荷载下胶合木梁跨中截面的剪力（N）；SZ为构件剪切面以上的截面积对中性轴的静矩（mm3）；b为构件截面中心轴位置的宽度（mm）；IZ为构件的全截面抗弯惯性矩（mm4）。

胶合木梁抗剪极限强度随着构件尺寸的增大而降低，存在尺寸效应。本研究采用Rammer[8]木梁抗剪强度公式（2），计算胶合木倒T 梁的极限抗剪强度：

式（2）中：τ为胶合木梁抗剪极限强度；Kf为调整木材实际破坏强度的应力集中因子，取值2；τASTM为木材顺纹剪切强度，兴安落叶松木材顺纹径面剪切强度取8.5 Mpa[19]；A为倒T 梁的有效剪切面积。

取每组试件极限承载力的最大值计为计算剪力值（A 组68 kN、B 组62 kN），两组试件的中心轴均处于肋板截面（宽度75 mm），胶合木倒T 梁跨中截面最大剪应力试验值与剪切强度理论值的比较见表4，有效剪切面积引用midas civil 电算结果。由表4 可知，两组试件破坏时的最大剪应力与Rammer 公式计算的理论值符合较好。同时证明了Rammer 剪切强度公式不仅适用于矩形截面梁，也适用于非矩形截面倒T 梁的弯剪强度及弯剪承载力计算。

表4 胶合木倒T 梁极限剪应力试验值与理论值比较Table 4 Comparison of experimental values and theoretical values of ultimate bending shear stress of glulam T-beam

3 结论与讨论

3.1 结 论

为了增强胶合木梁的极限弯曲承载力、整体性和刚度，探索胶合木连续T 梁跨中负弯矩区段的抗弯特性，本研究提出了将翼缘板和腹板胶合形成T 形截面的构件形式。设计制作了两组不同高跨比的胶合木倒T 形截面简支梁，在两端简支条件下跨中加载，使肋板受压、翼缘板受拉，模拟胶合木连续T 梁支座界面负弯矩区段的抗弯特性。通过模型试验与理论分析再将理论结果和有限元模拟结果相对比的方法，实测分析了两组试件的应变、挠度、抗弯刚度、极限承载力及延性结果，观察分析了胶合木倒T 梁的破坏形态与破坏机理，最终得到以下结论：

1）试件的剪跨比A 组为5.24，B 组为6.11，两组试件均发生顺纹剪切破坏。当剪跨比大于6时，胶合木T 梁静力弯曲发生剪切破坏，基本符合《美国木结构规范ASTM D198》关于胶合木矩形梁破坏模式与剪跨比间关系的结论，但不完全一致，说明T 形梁的破坏模式与矩形梁不完全一致。

2）B 组与A 组试件相比，极限承载力降低10.4%，抗弯刚度降低36%，延性系数提高22.4%，表明随剪跨比增大，构件的极限承载力及抗弯刚度降低，但延性系数提高。

3）两组试件的荷载应变曲线在屈服点之前呈比例关系，满足平截面假定；两组试件均存在剪力滞效应，跨中截面翼板正应力横向分布不均匀，呈现随距离肋板中心越远而越小的关系。

4）本次试验倒T 梁的弯剪承载力采用Rammer剪切强度公式计算，理论与试验结果符合较好。

3.2 讨 论

通过对胶合木简支倒T 梁在跨中截面加载的方式，模拟连续T 梁支座负弯矩区段的抗弯特性，并用试验现象结合理论计算论证了破坏形式是顺纹剪切破坏这一结论；明确了剪跨比较大的情况下，胶合木T 梁（含倒T 梁）的破坏特征与矩形截面梁不完全一致。这是本研究的创新点。需待继续进行深入研究的问题如下：

1）2019 年 祝 明 桥 等[20]通 过 ANSYS 有 限元软件模拟研究了混凝土箱梁翼缘有效宽度计算系数，确定了主要影响因素，给出了在弹性阶段的承载能力极限状态计算模型。本研究引用的Rammer 抗剪强度计算模型与有效剪切面积呈幂函数反比例关系，而在T 形截面梁中有效剪切面积与翼缘板宽度有关，所以下一步对于T 梁有效翼缘宽度的研究可参考祝明桥提出的影响因素和计算模型。

2）T 形截面梁在翼缘板处存在剪力滞效应，所以对于胶合木连续梁桥支座区段的桥面板的剪应力防护措施需继续研究。

3）本研究虽指出了在剪跨比较大情况下胶合木T 梁的破坏形式与矩形截面梁不完全一致，但由于试件较少，截面类型不多，建议之后再增加试件个数和截面类型继续进行研究。

4）结合杨涛对胶合木T 梁正弯矩的研究及本文对负弯矩的研究，可基本得出胶合木T 形截面梁抗弯的破坏形式是顺纹剪切破坏，且破坏位置均在肋板部位，所以今后可对肋板的顺纹剪切破坏和防护措施进行深入研究。