基于FLAC3D的米贝复式滑坡稳定性分析

罗忠行，雷宏权

(1.湖南省核工业地质局三〇三大队， 湖南 长沙 410119；2.中南大学地球科学与信息物理学院，湖南 长沙 410112)

0 引言

当前，随着中国经济的高速发展，人们对自然环境的改造和利用日益强烈，越来越多的边坡稳定性分析及治理设计问题备受国内外学者关注和研究。早期的滑坡研究主要是针对土质滑坡，稳定性评价基于土力学的研究范畴，以材料力学及简单的弹塑性理论为基础的半经验半理论的研究方法[1]。到了19世纪中期，随着数学的不断发展加之人类面临着一系列的滑坡问题，研究人员主要是通过模型试验及大量的室内土工试验展开研究。20世纪60～70年代，对于滑坡的稳定性研究，主要是将地质分析和力学机制联系在一起。为了解决复杂的滑坡问题，研究人员将土体当作非均质的、各向异性的和非连续性的弹塑性体、黏弹性体或具有裂隙的脆性体来研究，并开始探索有限元在滑坡稳定性中的应用[2]。20世纪80年代以后，对于滑坡的稳定性研究趋于完善。在早期研究的基础上，建立了定量分析理论体系。与此同时，在计算机技术不断兴起的背景下，数值模拟已成为滑坡稳定性分析的一种重要方法[3]。本文以米贝复式滑坡为工程背景，在广泛分析国内外文献资料的基础上，运用简洁直观的数据处理技术，综合多种方法分析滑坡稳定性计算结果，为滑坡稳定性分析及治理工程设计提供参考。

1 工程概况

米贝滑坡位于中和溪南岸，米贝老街南侧山坡，其前缘临中和溪，背靠东西走向山体，地势整体南高北低。根据地质调查及钻探、井探揭露，米贝滑坡是由前后两个单体滑坡组成的复式滑坡，总体积2.575×105m3，为牵引式中型滑坡。目前H1滑坡周界特征明显，H2滑坡后缘周界特征较明显。H2滑坡以H1滑坡左壁作剪出口，滑坡总体形态为“长舌状”(图1、图2)。现将两个单体滑坡特征分叙如下。

图1 滑坡区全景Fig.1 Panorama of landslide area

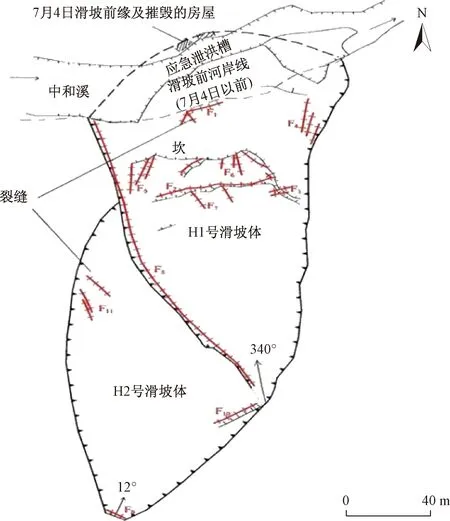
图2 滑坡平面示意图Fig.2 Geological map of landslide

H1滑坡：已发生整体滑动，仍然存在二次滑动的可能性，属典型活动滑坡。滑动体积约1.729×105m3，前缘水平滑距48 m；滑体由崩滑堆积体组成，总体上为双层土结构，上部为粉质黏土，下部为碎石，局部夹块石层，为滑动过程挤压、切割强风化岩石形成。滑坡体厚度6.0～16.0 m，平均厚度10.0 m；滑动面位于土、岩接触面，滑面因滑动磨蚀作用形成摩擦镜面。受滑坡扰动及拖曳，滑面处形成厚度约0.1～0.3 m 的滑带，物质组成主要为粉质黏土。本滑坡的滑面主要受岩土性质、岩层产状、节理裂隙、风化程度差异的影响，多段性特征较明显，大致呈折线形；滑床为上元古界板溪群五强溪组灰绿色、青灰色板岩，风化不均，局部强风化带厚达11.3 m，裂隙发育，裂隙率0.68%～1.59%。倾向为北西-北北西单斜岩层，倾向320°～340°，倾角30°～40°。

H2滑坡：处在蠕变阶段，滑坡局部变形，主要集中在坡体上部，为新滑坡。体积约8.46×104m3；滑体由第四系残坡积层及上元古界板溪群五强溪组板岩层组成。滑坡体厚度4.1～10.5 m，平均厚8.0 m；主滑面暂未形成，根据钻探及浅井揭露显示，局部位置揭露到滑带，厚度0.1 m，同时考虑坡体稳定的不利因素，综合确定潜在滑动面为土体与岩层界面或岩体内层面，埋深、滑带的物质组成与滑体土基本相同。土体与岩层界面的滑动面主要受岩土界面的起伏而变化，大致呈折线形；岩体内层面的滑动面主要受岩层产状的控制，基本为一平面，仅局部因产状的变化而稍有起伏。

滑坡区的地表水，随季节性变化大，多顺坡向排泄。地下水类型包括松散岩类孔隙水和基岩裂隙水，主要来源于大气降水及地表水补给，以渗流的形式排泄于坡脚、沟谷和陡坎之下或前缘河道内。

本滑坡的稳定性受多种因素影响，根据现场勘查资料分析，大气降水对滑坡变形起到促进作用。滑体表层土孔隙大，结构松散，大气降水容易入渗。本区属亚热带湿润气候区，雨量充沛，暴雨具有强度大，时间短的特点，雨水入渗增加了坡体堆积物的自重和下滑力，坡体稳定性变差。此外结合降雨资料，2014年6月1日—7月5日，米贝总降水量449.0 mm，比历史同期的224.1 mm多224.9 mm；特别是7月1—4日，连续4天强降水，总降雨量147.6 mm，持续性降雨造成土壤水分长时间处于饱和状态，易诱发滑坡地质灾害。为考虑滑坡的最不利状态，本文选用两种计算工况，即天然工况：自重+地下水位、暴雨工况：自重+暴雨+地下水位。

2 整体强度折减法分析H1滑坡稳定性

2.1 FLAC3D计算原理

如图3所示，在计算滑坡稳定性系数时，首先选取坡体内任一点A，其应力状态可以用应力莫尔圆表示。A点未进行折减时，其强度包络线位于莫尔圆之上。对A点逐步进行折减时，强度包络线会逐步下移，当包络线与莫尔圆相切时，该点达到其临界平衡状态，开始破坏，此时A点的应力状态即为强度折减后修正的应力状态。当坡体内类似A点的破坏点逐渐增多时，边坡开始出现整体变形。此时，边坡塑性区贯通，软件会出现发散现象，此时的折减系数即为边坡的最小安全系数[4-5]。

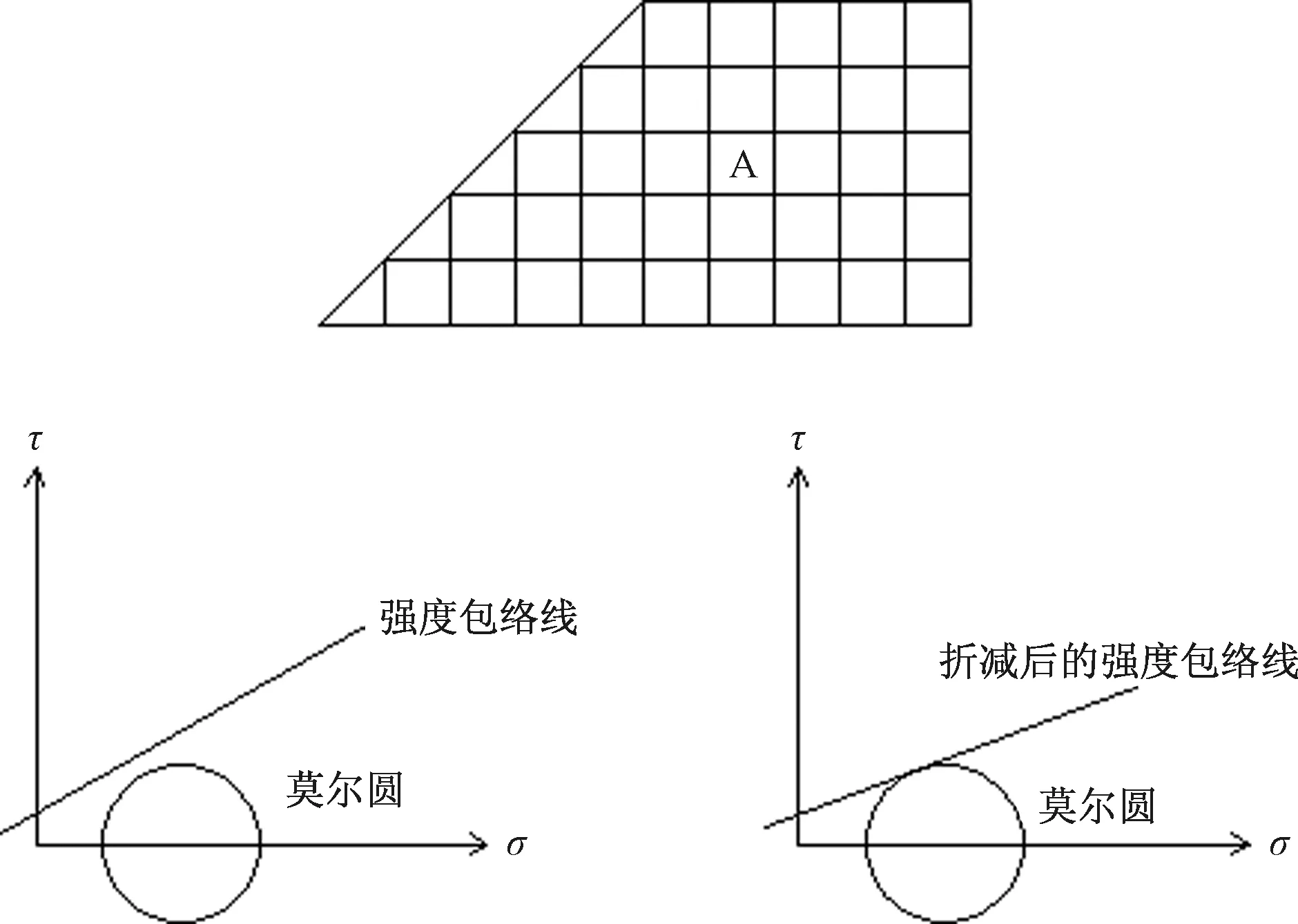
图3 强度折减法示意图Fig.3 Diagram of strength reduction method

在FLAC3D中，采用软件内嵌solve fos命令自动查找边坡的安全系数，其原理即为强度折减。该命令利用式(1)、(2)，对岩土体黏聚力c及内摩擦角φ进行调整，通过不断的调整安全系数Ft，对边坡进行数值分析，当计算正好发散时，边坡达到临界破坏状态，求得安全系数Ft。

ct=c/Ft

(1)

φt=arctan(tanφ/Ft)

(2)

式中：ct——折减后黏聚力；

φt——折减后内摩擦角；

Ft——折减系数。

2.2 模型建立

此次模拟基于米贝复式滑坡H1滑坡体B-B′剖面建模，考虑一个支护单元宽度，设置模型尺寸230 m×10 m×132 m，上部为自然地形；采用ANSYS划分网格，网格尺寸1.5～3.0 m，单元数18 920。采用摩尔库伦屈服准则，模型未施加水平及竖直向边界力，计算时仅考虑重力作用。几何模型及初始自重应力场见图4、图5。根据该滑坡实际情况特点，计算时考虑两种计算工况，天然工况和暴雨工况，考虑地下水对滑坡体的影响。

图4 地层及几何模型Fig.4 The model of stratigraphic and geometric

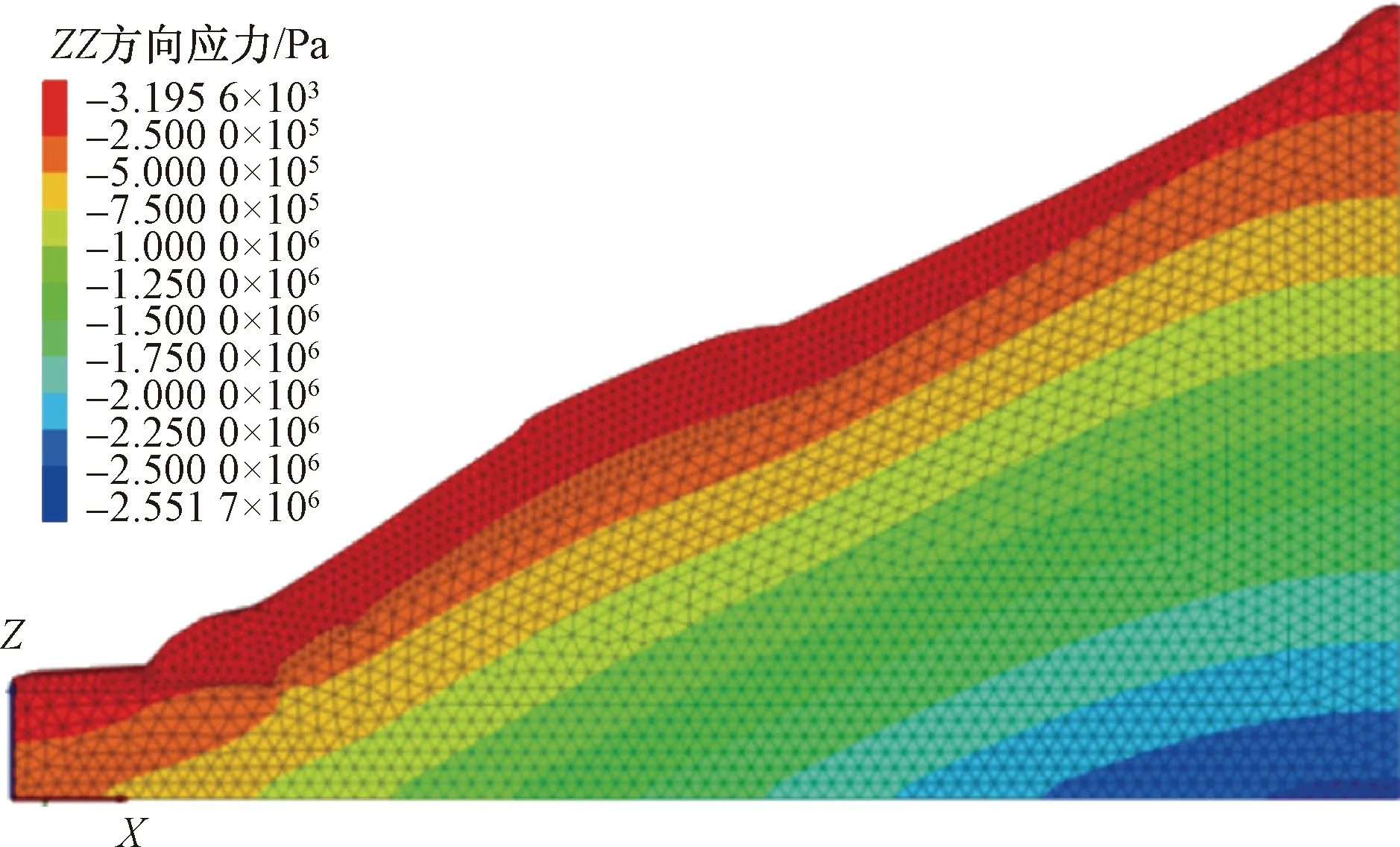
图5 初始自重应力场Fig.5 Initial self weight stress field

2.3 参数选取

计算参数主要参照勘查报告提供的数值，部分参数根据相同条件下的经验参数取值，其中H1滑坡滑动带抗剪强度参数见表1。

2.4 FLAC3D求解过程

采用FLAC3D强度折减法求解滑坡安全系数时，通常通过内置solve fos命令及自编强度折减法实现。自编强度折减法原理即为二分法原理，地层的黏聚力c、tanφ采用相同的折减系数Ks。每步折减后，若不收敛，则Ks向下二分；若收敛，则Ks向上二分；最终Ks收敛，通过记录Ks变化曲线，得到滑坡稳定系数。

表1 H1滑坡滑动带抗剪强度参数

本文通过FLAC3D强度折减法计算H1滑坡天然工况及暴雨工况下稳定系数，计算模型及参数见表1，采用自编强度折减法编写命令流。

计算饱和工况时，根据勘查剖面图，建立地下水面，并赋予水压力，对岩土体参数采用饱和强度计算。

2.5 FLAC3D求解结果及分析

运行命令流后，调整背景颜色为白色，通过输入 Plotfos cont ssi outline on vel red命令，分别输出天然状态及饱和状态下的安全系数，剪切应变增量及速度矢量图。

2.5.1天然状态

①通过图6可以看出，利用FLAC3D强度折减法计算出来的滑坡天然状态下稳定系数是1.098，说明该滑坡目前处于基本稳定状态。

图6 Ks折减过程曲线Fig.6 Curve of Ks reduction process

②通过图7可以看出，滑坡在自重应力作用下达到平衡，滑体变形位移呈现出规律性变化：滑坡中后缘(剖面凸起处)位移达到0.1～0.3 m，与现场后缘裂缝宽度较为一致；滑坡前缘位移量达到0.3～0.5 m，且越靠近临空面变形位移值越大，与现场滑坡前缘出现鼓胀现象较吻合。从位移变化规律可以看出，该滑坡位移分布相对均匀，滑体沿滑动面呈现整体滑动迹象，滑面以下滑床部分位移值相同，处于稳定状态；此外，滑坡前缘位移明显大于滑坡后缘，坡体向临空方向剪切蠕动，滑坡变形破坏模式应属于牵引式滑坡。

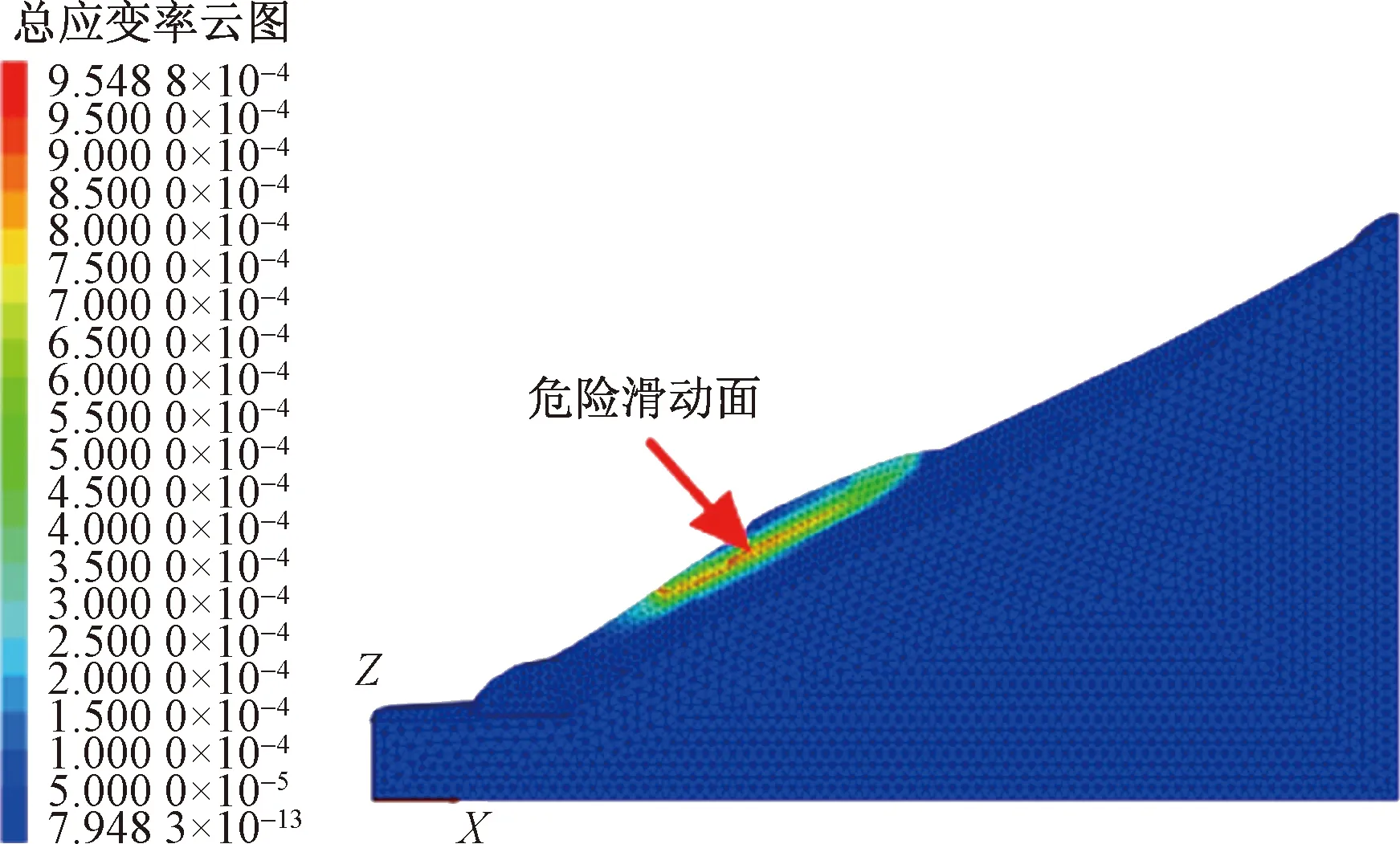
图7 总应变率云图Fig.7 Total strain rate nephogram

③从图8、图9可以看出，正处于剪切屈服状态，单元连成的条形区域已基本贯通整个滑坡体，塑性贯通区即为潜在滑动面位置。从速度矢量图可以看出，天然状态下，滑面以上网格位移速度明显大于其他区域位移速度，说明该区域滑体已发生明显变形(破坏)，滑坡整体稳定性较差。

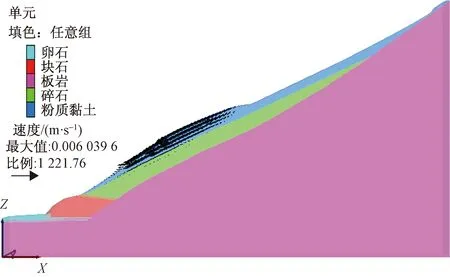
图8 速度矢量图Fig.8 Dagram of velocity vector

图9 应变增量分布图Fig.9 Dagram of strain increment

2.5.2饱和状态

①通过图10可以看出，利用FLAC3D强度折减法计算出来的滑坡暴雨状态下稳定系数是0.973，说明该滑坡在连续强降雨状态下会发生整体滑动。

②通过图11可以看出，在强降雨作用下，滑坡体内地下水位上升，滑体变形位移较之天然状态下发生较大变化：滑坡中后缘(剖面凸起处)最大位移达到0.5 m，说明裂缝随着强降雨条件会进一步扩展，有形成后缘陡坎趋势；滑坡前缘靠近临空面变形位移值达到4.5 m，说明该滑坡在强降雨作用下坡体发生整体滑动，部分松散体会堆积至滑坡前缘。与Ks折减计算出安全系数0.973比较吻合。

图10 Ks折减过程曲线Fig.10 Curve of Ks reduction process

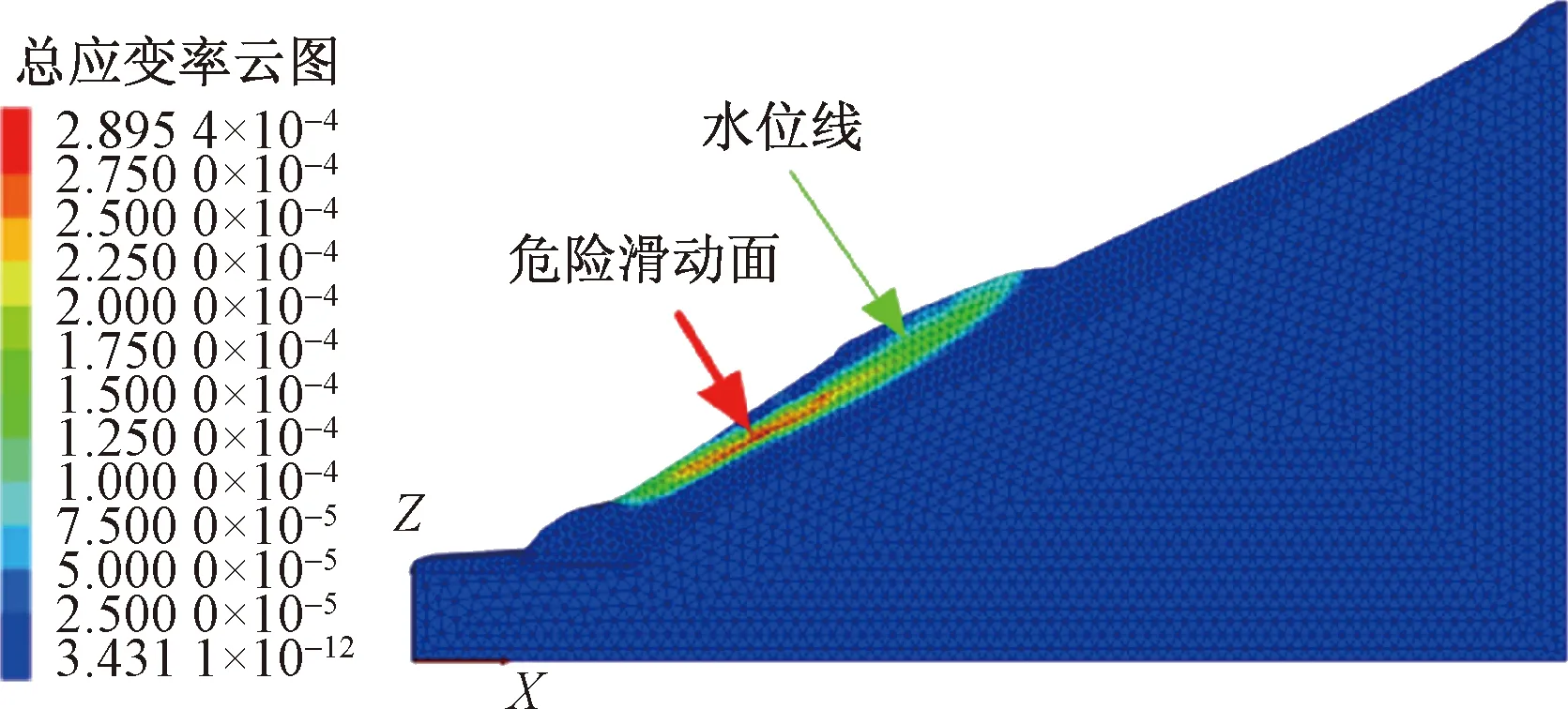
图11 总应变率云图Fig.11 Total strain rate nephogram

③从图12、图13可以看出，正处于剪切屈服状态单元连成的条形区域已贯通整个滑坡体，滑动面已完全贯通，坡体发生整体滑动。速度矢量图有力佐证这一分析，滑面以上网格位移速度远大于其他区域位移速度，说明该区域滑体已发生明显破坏，滑坡整体稳定性差。

3 双参数强度折减法分析H1滑坡稳定性

3.1 计算原理

双参数强度折减法较整体强度折减法原理区别在于对黏聚力及内摩擦角采用不同的折减系数进行折减，能够准确的反映黏聚力及内摩擦角在坡体滑动时发挥的先后顺序及贡献程度。采用双参数进行折减，需要解决的问题有两个。一是黏聚力及内摩擦角折减系数关系的确定；二是安全系数的求解。袁维[6]提出，c-tanφ临界曲线(图4)及其表达式：

(3)

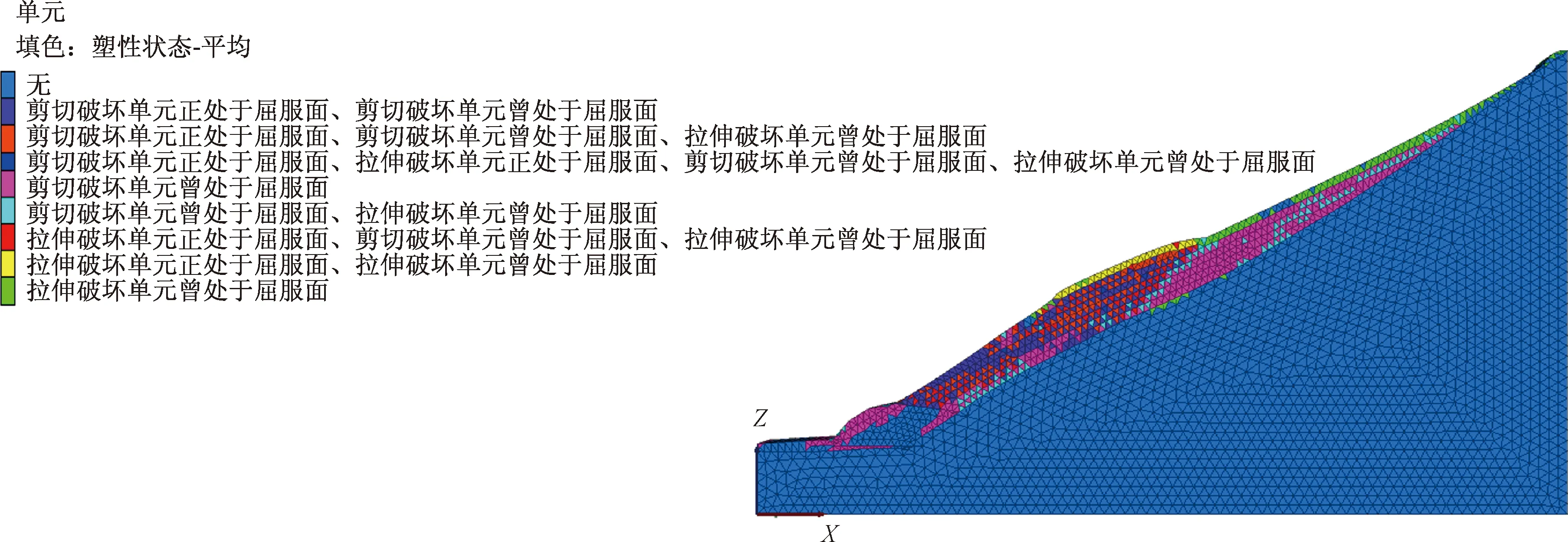
图13 应变增量分布图Fig.13 Dagram of strain increment

式中：c——黏聚力；

φ——内摩擦角；

m、n、h——待定系数。

分析图14可知使边坡达到临界状态的折减路径有无数种，依据最小值原理，边坡失稳时，必将沿着一个抗滑力最小的面滑动，因此临界滑动面的搜索就可以转化为P点距离曲线最短距离的求解问题。定义P点到曲线的距离为D，表达式如下：

(4)

根据式(4)，当D2取最小值时，定义此时的黏聚力值为cr，根据公式(3)可求得此时的tanφr。由此可求得黏聚力及摩擦角对应的折减系数：

(5)

式中：kc，kφ——黏聚力及内摩擦角对应的折减系数。

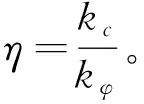
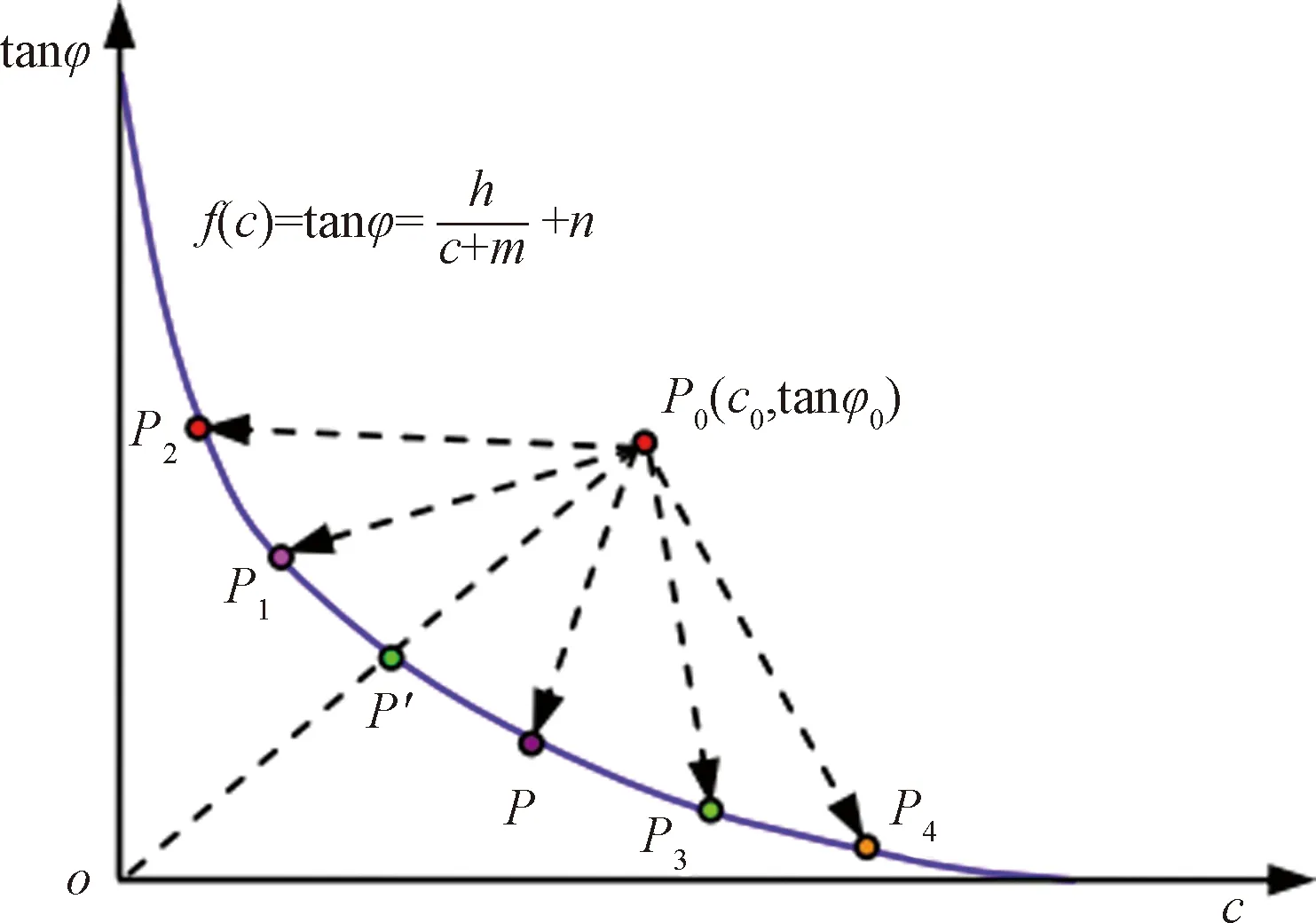
图14 边坡整体安全系数的定义Fig.14 Definition of overrall safety factor of slope

基于以上研究，本文参照前人[7]提出的一种计算安全系数的方法，对米贝滑坡整体稳定性进行分析计算，即：

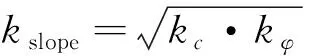
(6)

式中：kslope——边坡的整体安全系数。

3.2 基于FLAC3D双参数折减法计算方法

3.3 FLAC3D求解结果及分析

通过以上命令计算，输入 Plotfos cont ssi outline on vel red命令，输出kslope折减过程曲线，剪切应变增量及速度矢量图。

3.3.1天然状态

①通过图15可以看出，利用FLAC3D双参数强度折减法计算出来的滑坡天然状态下稳定系数是1.024，说明该滑坡目前正处于欠稳定状态。

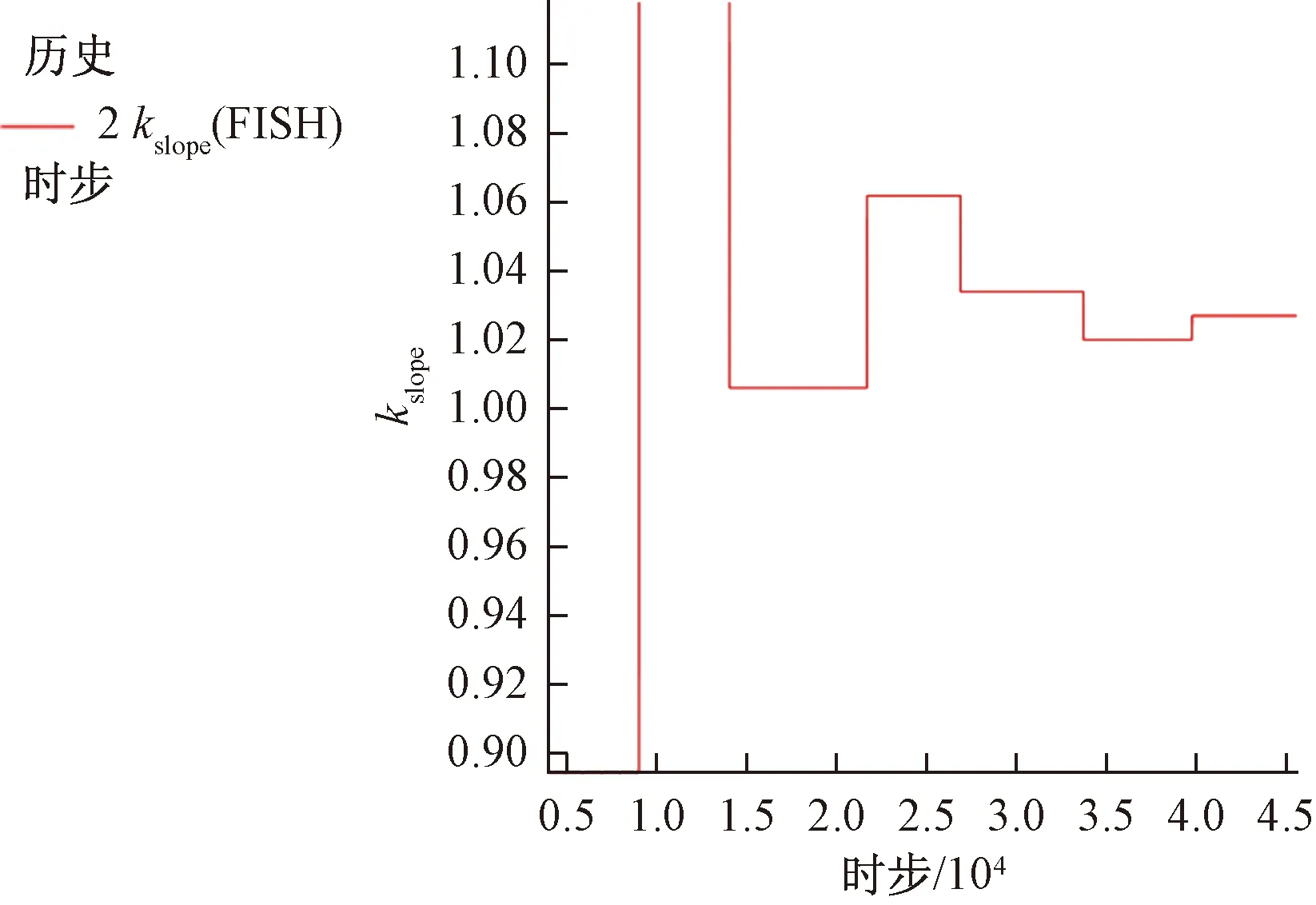
图15 kslope折减过程曲线Fig.15 Curve of kslope reduction process

②通过图16可以看出，滑坡最大位移出现在滑坡前缘，位移值在0.5～0.58 m，坡体中后缘位移值0.2～0.4 m，该值变化规律及范围与整体强度折减法较为一致。从位移云图可以看出，该滑坡位移分布相对均匀，滑体沿滑动面呈现整体滑动迹象，坡体向临空方向剪切蠕动，滑坡变形破坏模式应属于牵引式滑坡。

图16 总位移云图Fig.16 Total strain rate nephogram

③从图17、图18可以看出，正处于剪切屈服状态的单元连成的条形区域已基本贯通整个滑坡体，塑性贯通区即为潜在滑动面。从速度矢量图可以看出，天然状态下，滑面以上网格位移速度明显大于其他区域，说明该区域滑体已发生明显变形(破坏)，与该滑坡处于欠稳定状态较为吻合。

图17 速度矢量图Fig.17 Dagram of velocity vector

图18 塑性区分布图Fig.18 Dagram of strain increment

3.3.2饱和状态

①通过图19可以看出，利用双参数强度折减法计算暴雨状态下滑坡稳定系数是0.891，说明该滑坡在连续强降雨状态下会发生整体滑动。

图19 kslope折减过程曲线Fig.19 Curve of kslope reduction process

②通过图20可以看出，在强降雨作用下，滑坡体内地下水位上升，滑体变形位移较天然状态下发生较大变化：滑坡中后缘(剖面凸起处)最大位移达到0.8～1.6 m，说明裂缝随强降雨条件会进一步扩展，形成后缘陡坎；滑坡前缘靠近临空面变形位移值达到2.0 m，说明该滑坡在强降雨作用下坡体发生整体滑动，部分松散体会堆积至滑坡前缘。与kslope折减计算出安全系数0.891比较吻合。

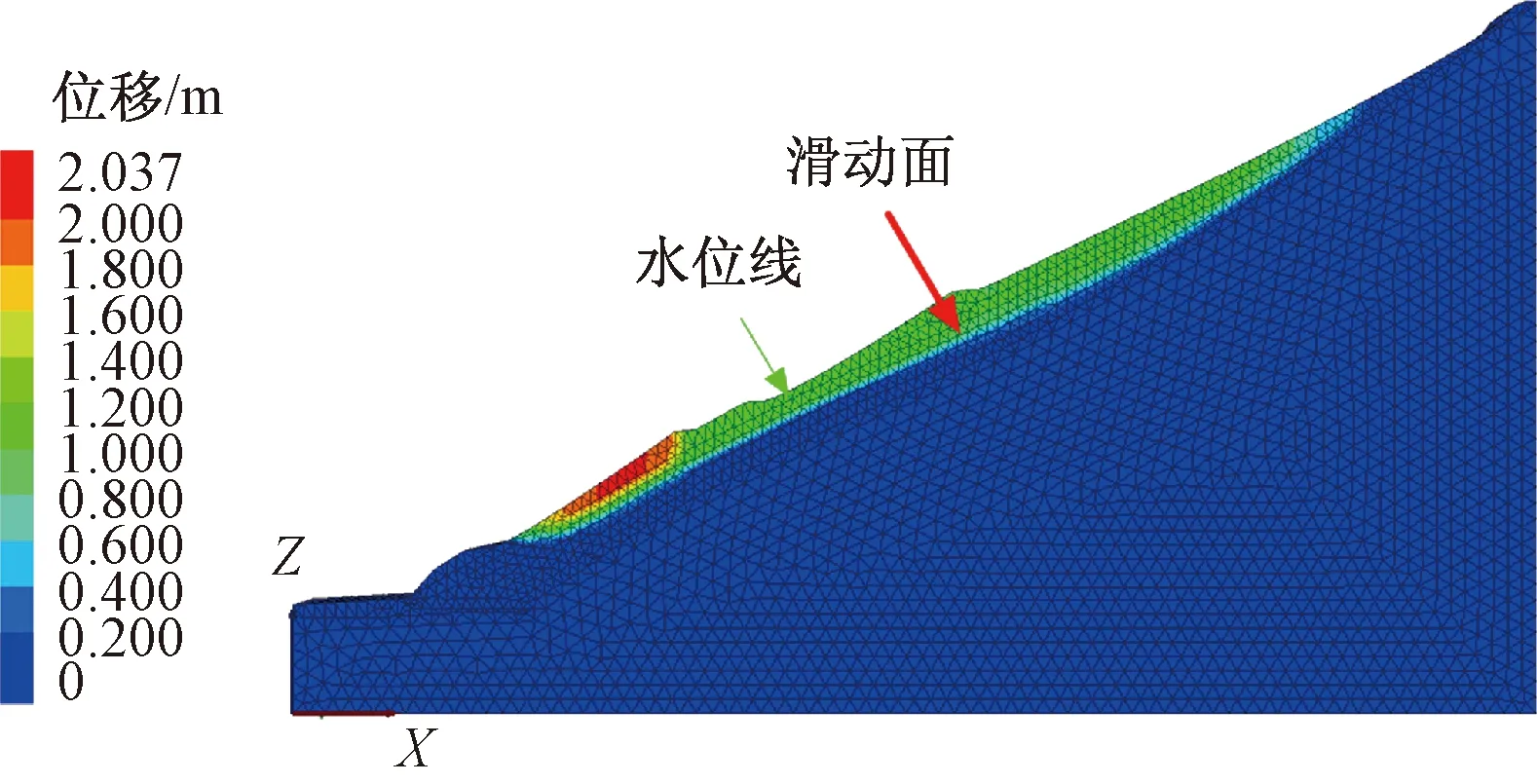
图20 总位移云图Fig.20 Total strain rate nephogram

图21 速度矢量图Fig.21 Dagram of velocity vector

③从图21、图22可以看出，正处于剪切屈服状态单元连成的条形区域已贯通整个滑坡体，滑动面已完全贯通，坡体发生整体滑动。速度矢量图有力佐证这一分析，滑面以上网格位移速度远大于其他区域位移速度，说明该区域滑体已发生明显破坏，滑坡处于不稳定状态。

4 两种计算方法对比分析

4.1 两种计算方法下安全系数比较

根据上文计算分析，针对H1滑坡，采用整体强度折减法和双参数强度折减法在天然状态和暴雨状态下分别计算的安全系数如表2所示。

表2 H1滑坡安全系数计算对比表

天然状态下，两种方法计算结果均大于1.0，小于1.1，说明滑坡处于欠稳定-基本稳定状态，滑体主要是坡面突出位置粉质黏土层，滑面深入到下部碎石层，两种方法评判结果基本一致。

暴雨状态下，两种方法计算结果均小于1.0，滑面和滑体扩展至坡脚，说明该滑坡在强降雨作用下，处于不稳定状态，会发生整体失稳破坏，需要进行治理。

4.2 两种计算方法滑面位置比较分析

两种折减法搜索到的滑坡最危险滑动面较为接近，但仍存在差异。采用双参数强度折减法得到的滑面比整体强度折减法的要深，更接近滑坡勘查揭露滑面位置，塑性区范围要大，显示更清楚。

从现场实际情况及工程安全的角度出发，采用双参数折减法分析的结果更接近实际情况，边坡治理后安全性较高(图23、图24)。

图22 塑性区分布图Fig.22 Dagram of strain increment

图23 天然状态下滑动面差异Fig.23 Difference of sliding surface in natural state

图24 暴雨状态下滑动面差异Fig.24 Difference of sliding surface in rainstorm state

5 基于双参数强度折减法的H2滑坡稳定性分析

5.1 模型建立及计算参数选取

采用H2滑坡主剖面F-F′剖面建模，考虑一个支护单元宽度，上部为自然地形；采用ANSYS划分网格，共划分8 700个节点，4 218个六面体单元。模型未施加水平及竖直向边界力，计算时仅考虑重力作用。几何模型及初始自重应力场见图25、图26。计算参数主要参照勘查报告提供的数值，部分参数根据相同条件下的经验参数取值，其中H2滑坡滑动带抗剪强度参数见表3。

表3 H2滑坡滑动带抗剪强度参数

图25 地层及几何模型图Fig.25 The model of stratigraphic and geometric

图26 初始自重应力场Fig.26 Initial self weight stress field

5.2 双参数折减法分析滑坡稳定性

根据H2滑坡实际情况特点，计算时考虑两种计算工况：天然工况和暴雨工况，考虑地下水对滑坡体的影响。本次计算采用最小值原理及自编强度折减法，对H2滑坡进行稳定性计算分析。计算结果如下：

5.2.1天然状态(图27～图30)

图27 kslope折减过程过程曲线Fig.27 Curve of kslope reduction process

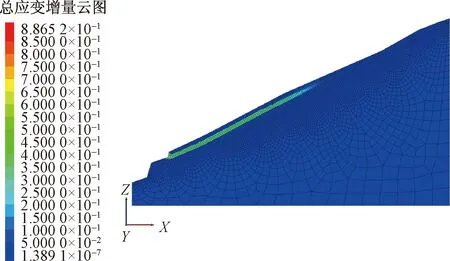
图28 总位移云图Fig.28 Total strain rate nephogram

图29 速度矢量图Fig.29 Dagram of velocity vector

图30 塑性区分布图Fig.30 Dagram of strain increment

5.2.2饱和状态(图31～图34)

图31 kslope折减过程曲线Fig.31 Curve of kslope reduction process

图34 塑性区分布图Fig.34 Dagram of strain increment

(1)通过kslope折减过程过程曲线可以看出，利用FLAC3D双参数强度折减法计算出来的H2滑坡天然状态下安全系数是1.124，说明该滑坡目前正处于基本稳定状态;暴雨状态下安全系数为0.912，该滑坡在连续强降雨状态下已经处于失稳状态。

(2)通过对比分析两种工况下的整体位移云图，可以看出：天然工况下滑坡最大位移出现在滑坡前缘，坡体位移分布相对均匀，滑体沿滑动面呈现整体滑动迹象，坡体向临空方向剪切蠕动，滑坡变形破坏模式应属于牵引式滑坡。在强降雨作用下，滑坡体内地下水位上升，滑体变形位移较之天然状态下发生较大变化：滑坡中后缘位移变化急剧增加，说明裂缝随着强降雨条件会进一步扩展，形成后缘陡坎；滑坡前缘靠近临空面变形位移值达到0.977 m，说明该滑坡在强降雨作用下坡体发生整体滑动，部分松散体会堆积至滑坡前缘。

(3)从塑性区云图可以看出，天然状态下坡体塑性区的底部，基本上处于剪切屈服状态，代表单元处于剪切屈服状态，该部分单元连成的条形区域已基本贯通整个滑坡体，即塑性贯通区即为潜在滑动面位置，这也与总应变率云图揭示的滑动面位置相吻合。暴雨状态下，处于剪切屈服状态的单元连成的带状区域已贯通整个滑坡体，滑动面已完全贯通，坡体发生整体滑动。

5.3 H2滑坡稳定性状态预测分析

综合分析位移变形云图，可以发现天然状态塑性区均位于土层中，上部为拉塑性区、下部为剪塑性区；饱和状态时当前塑性区沿岩-土接触面扩展。滑坡前缘形变量较后缘变形量大，在其前缘形成临空面，坡体内部应力发生改变，后缘相继形成张拉裂缝，滑坡处于极限平衡状态。因此，按照滑坡受力状态，该处滑坡应属于牵引式滑坡。在持续强降雨等不利条件下，H2滑坡发生整体滑动可能性较大，与现场滑坡监测数据及详细勘查结论基本一致。

6 数值模拟与极限平衡稳定性计算方法对比分析

为了进一步说明数值模拟方法的实用性及准确性，本文对H1滑坡B-B′剖面、H2滑坡F-F′剖面天然状态下，依据详细勘查成果，采用极限平衡法进行条分计算安全系数，两者计算结果对比表详见表3。

表3 安全系数计算结果对比表

对比以上两种计算方法可以看出:天然工况下，H1滑坡数值模拟法与极限平衡法计算得出的安全系数结果较为接近；H2滑坡数值模拟法计算得出的安全系数较极限平衡法略高。分析二者相同及差异原因，可得出以下结论：(1)H1滑坡属典型活动滑坡，滑面位置确定，滑带参数较准确，提高了极限平衡法安全系数计算的准确性，从而也说明基于双参数折减法滑坡安全系数计算结果的可靠性；(2)H2滑坡目前处于蠕动变形阶段，滑面未贯穿，极限平衡法基于详细勘查成果中推测的滑面位置及滑带参数进行条分理论计算；数值模拟法则基于滑坡应力场及坡体变形综合分析边坡滑动的最危险滑裂面，并得出相应的位移场、应力场在相应工况下的渐进破坏过程，其计算结果精度较高，更接近实际情况，成果资料更直观，更具有设计参考价值。

7 结论

(1)基于FLAC3D数值模拟方法对米贝复式滑坡稳定性进行分析计算，搜索到的滑动面位置、坡体变形位移与现场监测、地勘成果资料基本一致；H1滑坡天然状态下处于基本稳定状态，暴雨状态下处于不稳定状态，会发生二次整体失稳破坏；H2滑坡天然状态下处于基本稳定状态，暴雨状态下处于不稳定状态，存在整体滑动的可能。

(2)比较整体强度折减法与双参数强度折减法，两种理论确定的滑坡最危险滑动面较为接近，但仍存在差异。采用双参数强度折减法得到的H1滑坡滑面比整体强度折减法的要深，更接近详细勘查揭露滑面位置，塑性区范围要大，显示更清楚。从工程安全的角度出发，采用双参数折减法分析的结果比较保守，滑坡治理后安全性较高。

(3)针对蠕变型滑坡，数值模拟法较极限平衡法计算结果精度较高，更接近实际情况。该方法除了可提供可靠的安全系数外，还能直观的反映最危险滑面位置及应力场、位移场渐近破坏状态，可为工程最优设计参考。