多年冻土边坡的水热力耦合分析及软件开发
董旭光,董建华,何天虎,代 涛,孙国栋
(1.宁夏大学土木与水利工程学院,宁夏 银川 750021;2.兰州理工大学甘肃省土木工程防灾减灾重点实验室,甘肃 兰州 730050;3.兰州理工大学理学院,甘肃 兰州 730050)
0 引言
多年冻土占我国国土面积的21.5%,近年来在冻土区进行了大规模的土方开挖和填土工程建设,对地质环境的扰动使很多冻土边坡稳定性变差。如青藏公路K3057段附近发生融冻泥流滑坡,K3035段滑塌体在5年内向山顶后退约100 m,泥流滑塌体向青藏公路移动,即将影响公路的正常运营[1]。牛富俊等[2]将青藏高原冻土斜坡破坏划为:崩塌、蠕变、热融失稳和泥流等。边疆等[3]对多年冻土区的主要冻害类型和特征进行归类, 并提出防治措施。冯守中等[4]对寒区岩质和土质边坡进行破坏机理分析,并给出了相应稳定性计算方法。刘红军等[5]对寒区土质边坡冻融失稳及植被护坡进行了试验研究,监测表明:边坡冻结过程中,水分向冻结锋面迁移,木本植物护坡有助于减小边坡冻融失稳。靳德武[6]探讨了低角度冻土斜坡的破坏机理,进行了冻融模型试验,给出了不同渗流条件下冻土边坡稳定性分析方法。LI等[7]对玉树成都县支梅村秋季牧场边坡失稳进行了数值模拟,发现造成失稳的主要原因是季节性霜冻和持续降水下渗引起的基底抗剪强度降低。赵梦怡等[8]对康定县新都桥粗颗粒冻土道路边坡进行变形、气温、地温和地下水等长期观测表明:在冻结融化和积雪消融条件下,粗颗粒冻土边坡变形突增,坡面表层1 m内产生滑塌。董旭光[9]针对多年冻土热融滑塌,基于主动保护冻土理念,提出区新型框架热锚管边坡支护结构,模拟和验证表明结构降温效果良好、控制变形能力强。查阅大量文献可知,目前对冻土边坡研究还较少,由于冻土是一种对温度极其敏感的含冰体,冻土边坡病害与其中水分的冻融和迁移有密切关系。因此,冻融作用下边坡失稳是水热力共同作用的结果,故基于水热力耦合研究冻土边坡的稳定具有重要意义。
国内外对水热力耦合进行了大量研究,如HARLAN[10]提出水-热耦合模型,随后又提出分凝势、水热力耦合和刚体冰模型等。陈飞熊[11]建立了全面考虑冻土中骨架、冰、水三相介质水、热、力与变形耦合的数理方程。李洪升等[12]将冻土视为弹性均质体,推导了冻结过程中水分、温度和应力耦合控制方程。LI等[13]在考虑冻土流变的弹黏塑性本构模型基础上,建立了描述土体冻融过程的水-热-力相互作用理论模型,并对某水渠进行了计算。MA等[14]讨论了冰-水相变广义Clasusius-Clapeyron方程的适用条件,并提出了更能真实反映土体冻结过程的动态模型。这些研究成果为分析冻土边坡稳定提供了坚实基础,然而水热力多场耦合计算过程复杂,传统的软件还无法直接模拟土体“冻胀融沉”现象,需要通过等效简化,为工程问题分析带来不便。因此,开发多场耦合分析软件对快速计算冻土边坡冻融反应特性有重要价值。
本文基于水热力三场耦合理论,编写了能反应土体冻胀融沉的多场耦合计算程序,开发了冻土边坡水热力耦合分析软件,建立了多年冻土边坡多场耦合计算模型,分析了冻融作用时边坡的温度、水分、应力和变形分布规律,为冻土边坡工程计算提供方便及参考。
1 冻土边坡水热力耦合控制方程
在周期性冻融循环作用下,冻土骨架和水的热传导及冰-水相变作用,则冻土边坡中温度满足带相变瞬态温度场的热传导方程为[11]:
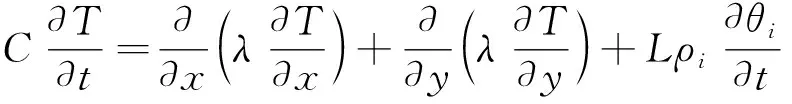
(1)
式中:C——体积比热容;
T——温度;
t——时间;
x、y——坐标系;
λ——导热系数;
L——相变潜热;
ρi——冰的密度;
θi——冰的体积含量。
冻融作用下冻土边坡中水分迁移以液态水进行,则水分迁移方程为[12]:

(2)
式中:θu——未冻水体积含量;
D——水分扩散系数;
ρw——水的密度。
冻土未冻水含量与温度的联系方程为:
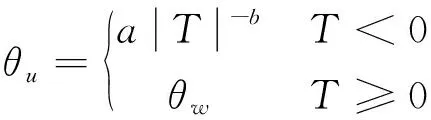
(3)
式中:a、b——与土体性质有关的参数;
θw——总含水量。
将式(1)代入式(2),并由(3)式的导出关系化简得到水热耦合方程为:
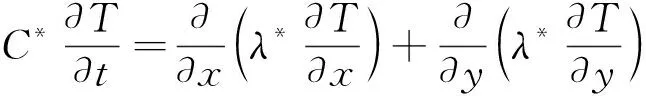
(4)

采用显热容法来考虑相变面,假设土体相变发生在Tm附近的一个温度范围内(Tm±ΔT),则简化构造出体积热容和导热系数表达式为[15]:

(5)

(6)
式中:Cf——冻土比热容;
λf——冻土导热系数;
Cu——融土比热容;
λu——融土导热系数;
Tm——相变区间中点温度;
ΔT——相变区间中点温度与最高或最低相变温的绝对差值。
冻土边坡的静力平衡微分方程为:
[∂]{σ}-{f}=0
(7)
物理方程为[12]:
{σ}=[DT]({ε}-{εv})
(8)
几何方程为:
{ε}=[∂]T{u}
(9)
式中:[∂]——矩阵微分算子;
{σ}——应力;
{f}——体力;
[DT]——与温度有关的弹性矩阵;
{ε}——弹性应变;
{εv}——冻胀或融化引起的应变;
{u}——位移。
其中,
冻结时,
融化时,
式中:E——弹性模量;
μ——泊松比;
θ0——初始含水量;
Δθ——在一定时间内的水分迁移量;
n——土的孔隙率;
A——融沉系数;
a1、b1、a2、b2、m——与土性有关的参数,取值参见文献[15-16]。
方程(1)~(9)组成了多年冻土边坡的水热力耦合方程组。由于土体热力学参数随温度而变化,并在计算模型区域内有一个随时间变化的冻融界面,冻融界面产生相变,因此,上述方程描述的是一个大空间大时间尺度的强非线性问题,无法获得解析解,故采用数值方法进行求解,本文将冻土边坡控制方程在空间域采用有限元离散,时间域采用有限差分离散,两者相结合迭代求解,基于Matlab平台开发多年冻土边坡多场耦合计算软件。
2 程序验证及软件开发
2.1 文献程序验证
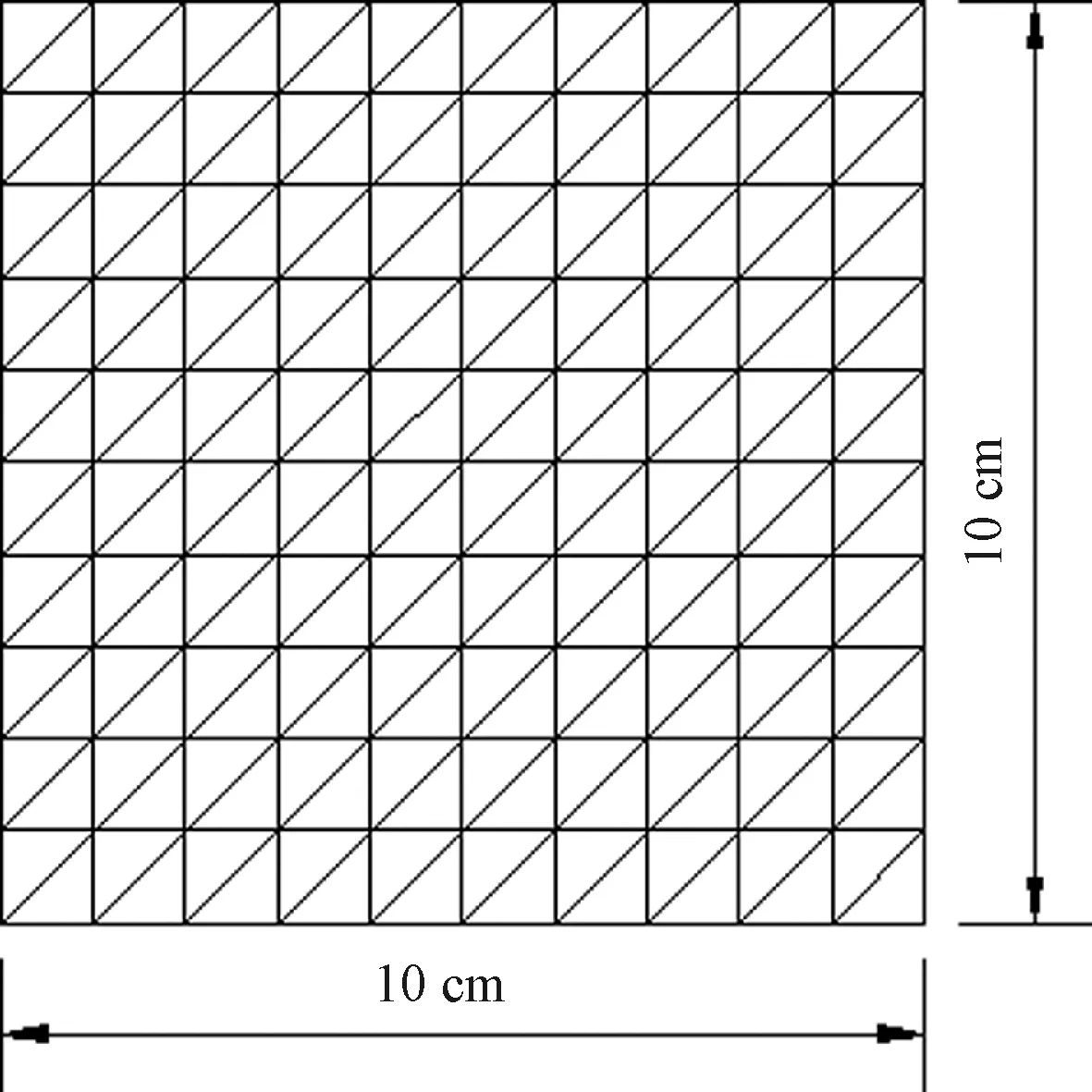
图1 PENNER实验试样的有限元数值分析模型Fig.1 FEM of PENNER experiment
为了检验编制的水热力耦合程序的正确性,采用PENNER[17]研究冻土冰透镜体形成过程实验和MU等[18]对该实验数值计算,验证本文水热力耦合程序的正确性。土体热学、力学参数和边界条件均与文献相同,分析模型见图1,温度边界见图2。利用开发的程序计算,选取冻结深度和冻胀量进行对比分析,结果如图3和图4所示。
试验用土的含水量为0.35,未冻水和土体负温之间的函数关系[18]:

冻土视为线弹性体,冻土和未冻土泊松比均取0.3,未冻时弹性模型11.2 MPa,冻结时弹性模量为:

(11)
土体导水系数用Horiguchi实验结果:

(12)
温度初始和边界条件:土体顶部为暖端;底部为冷端,进行由下向上冻结。边界条件如图2所示[17-18]。为了模拟冻结前试样的初始状态,将t=0时刻的上边界和下边界温度作为初始温度,利用初始温度条件和土体的热参数及其它特性参数求解Laplace方程,求得计算区域温度场的估计值,修正参数,再继续计算直至稳定温度场作为初始温度场。
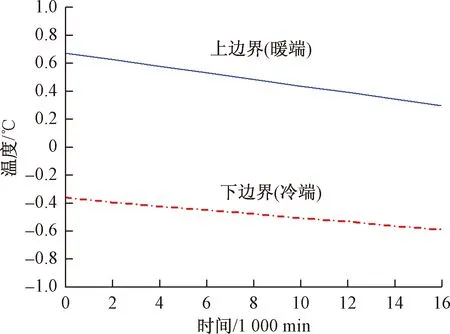
图2 温度边界条件Fig.2 Boundary conditions of temperature
水分边界条件:土体内为饱和土体,冻结时从底部边界(从暖端)进行水分补给。
位移边界条件:土体底部约束,左右两侧为法向约束,顶部为自由位移边界。
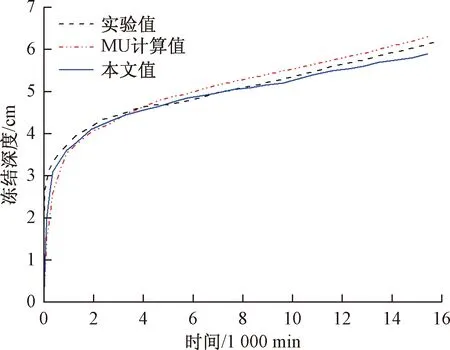
图3 冻结深度随时间变化的曲线Fig.3 Freezing depths at different time

图4 冻胀量随时间的变化曲线Fig.4 Variation of heave deformation with time
由图3和图4可知,本文得到不同时刻的冻结深度比实验值略小,而比MU[18]计算结果更接近试验值;各时刻冻胀量比实验值稍小,与MU[18]计算相比前半段偏大,后半段偏小。综合可知,本文得到的冻结深度和冻胀量的变化规律与PENNER实验MU分析结果规律相符,数值相近,说明编制的程序是可靠和有效的。
2.2 软件开发
依托MATLAB[19]平台,基于水热力耦合理论,开发了可独立运行、面向对象、界面友好和操作简便的多年冻土边坡水热力耦合分析软件。该软件包括前处理器(模型尺寸、土体物理参数的输入和网格划分),求解器(迭代求解)和后处理器(结果保存和云图显示),开发流程图如图5所示,软件主界面、模型生成、参数输入和计算结果显示界面见图6~图7。该软件能高效、准确实现外界温度作用下多年冻土边坡的温度、水分、应力和位移计算,对冻土边坡工程计算有重要的理论意义和应用价值。
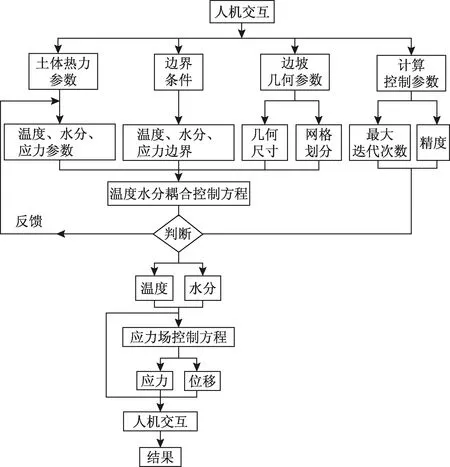
图5 软件程序设计框图Fig.5 Design diagram of software

图6 软件主界面Fig.6 Main interface of software
3 算例分析
3.1 计算模型
青藏高原大阪山地区某多年冻土边坡,坡高5.0 m,坡度45°。该地区气温变化曲线为Ta=-3+12sin(2πt/8 760+π/2),土层为单一均质饱和黏土,土体物理参数见表2,土体干密度ρd/(kg/m3),初始含水量θo,冻土未冻水含量与温度关系参数a和b;弹性模量,泊松比与温度关系参数a1、b1、a2、b2和m;融沉系数A;热学参数见表3,融土热容Cu/(J·kg-1·℃-1),导热系数λu/(J·m-1·℃-1)和水分扩散系数Du/(J·m-3·℃-1);冻土热容Cf/(J·kg-1·℃-1),导热系数λf/(J·m-1·℃-1)和水分扩散系数Df/(J·m-3·℃-1),有限元计算模型见图8。
图7 温度云图绘制界面Fig.7 Interface of the temperature nephogram
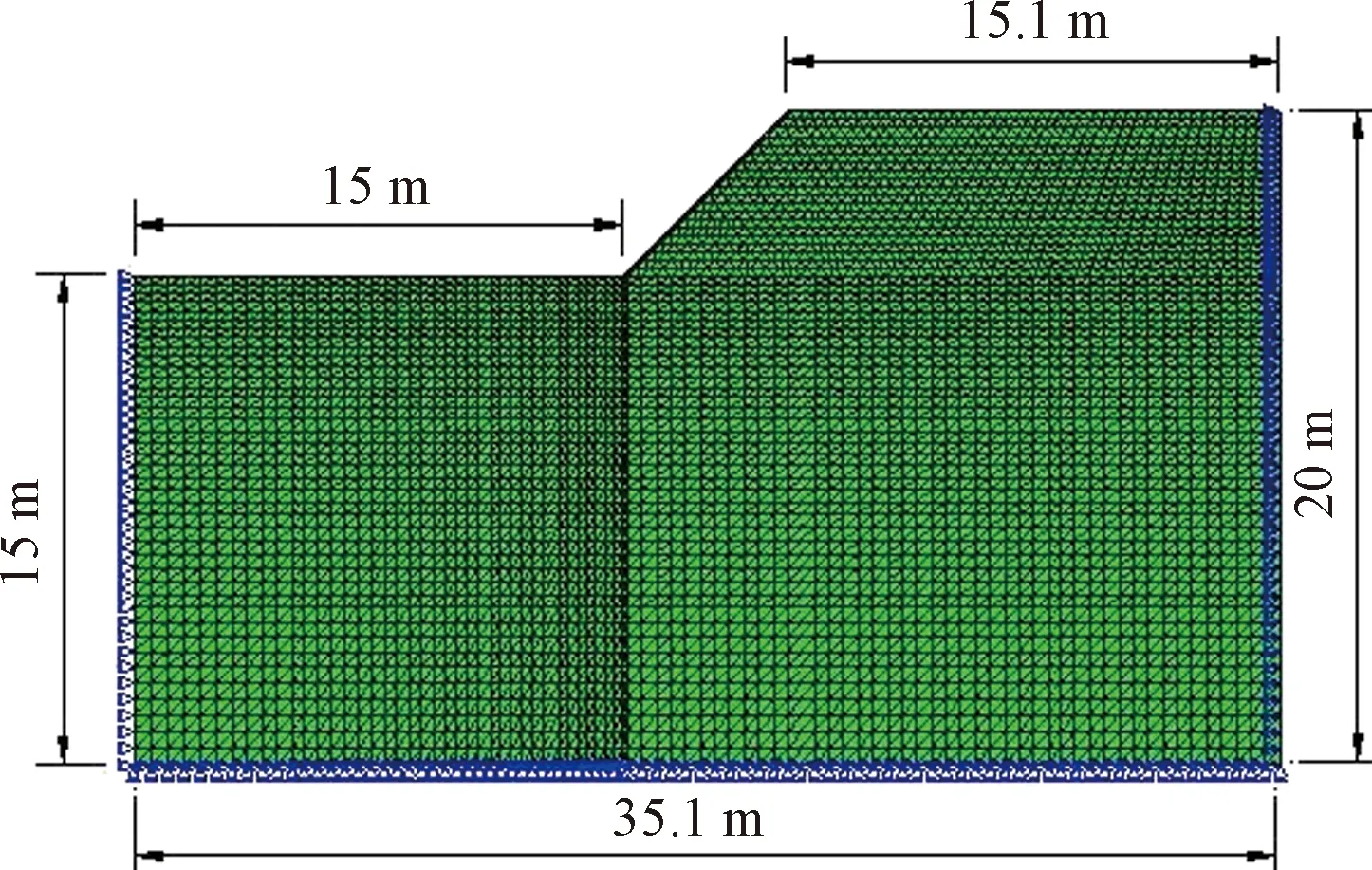
图8 有限元计算模型Fig.8 Calculation model of finite element
3.2 边界条件和初始条件
温度边界:根据实测结果,坡面为Ts=0.7+13sin(2πt/8 760+π/2),坡脚和坡顶为Ts=-1.5+12sin(2πt/8 760+π/2),两侧绝热,底边热流密度为0.06 W/m2。
水分边界:不考虑水分与外界蒸腾和入渗交换。
位移边界:两侧边为水平支撑,底边为水平和竖向支撑,其余各边自由。
求解过程:含水率取冻土边坡实际值,然后给温度赋予初始值,结合边界求解式(4)和(2),进行冻融循环计算,直至季节活动层以下的温度和水分保持稳定,同一时刻各节点值逐年相同为止,以此时各节点的温度、水分作为冻土层稳定的初始值,再求解式(7)~(9)得到初始应力,重新计算外界季节冻融作用下,边坡土体的响应。
3.3 结果分析
边坡经历一个冻融周期,冻结期(寒季)从10月中旬至来年4月中旬(取4月15日),融化期(暖季)从4月中旬至10月中旬(取10月15日)。冻结期和融化期结束是边坡在冻融作用下的两个极端状态,选取这两个时刻进行冻融分析。

表2 边坡土体力学参数

表3 边坡土体热学参数
(1)冻融作用下边坡温度场分析
由图9可知,冻融作用下边坡的活动层发生冻融交替变化,不同时刻边坡温度场有明显差别。冻结结束时,边坡处于完全冻结状态,坡面负温较大的厚度比坡顶和坡脚均薄。融化结束时,坡面融化厚度比坡顶和坡脚都大,冻融对坡面温度影响较大,热融可引起边坡滑移,此与实际观测相符。
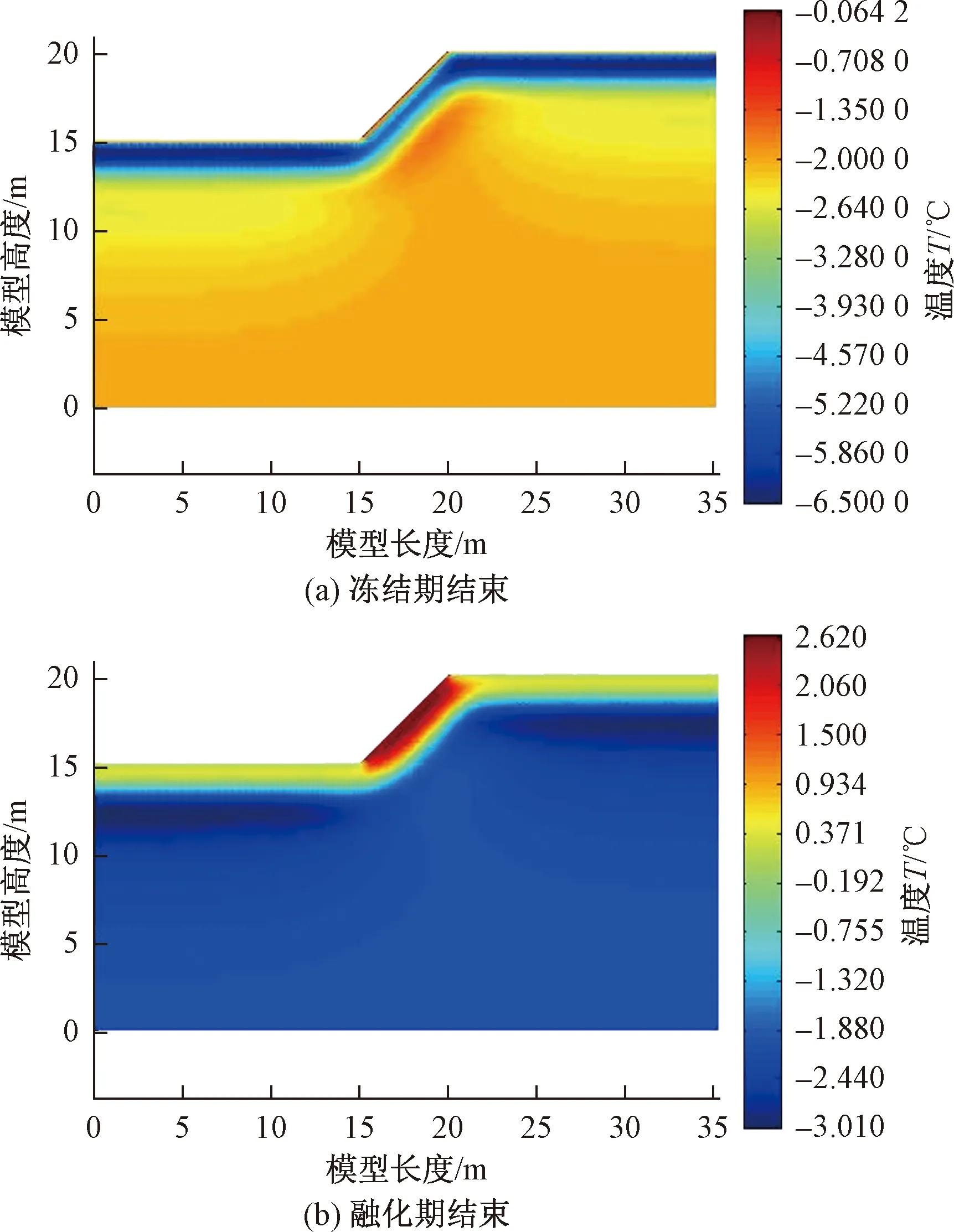
图9 不同时刻边坡温度云图Fig.9 The temperature of slope at different times
(2)冻融作用下边坡水分场分析
从图10可以看出,冻结期结束时,活动层土体的未冻水含量比其他部位低,未冻水含量与温度同步变化,大小由温度和土性共同决定。融化结束时,活动层土体的未冻水含量明显比其他部位高,在冻融交界面处最高,含水量最大值大于初始含水量20%。融化期结束时未冻水含量略大于冻结时,说明冻融作用下土体发生了水分迁移,总含水量增加。
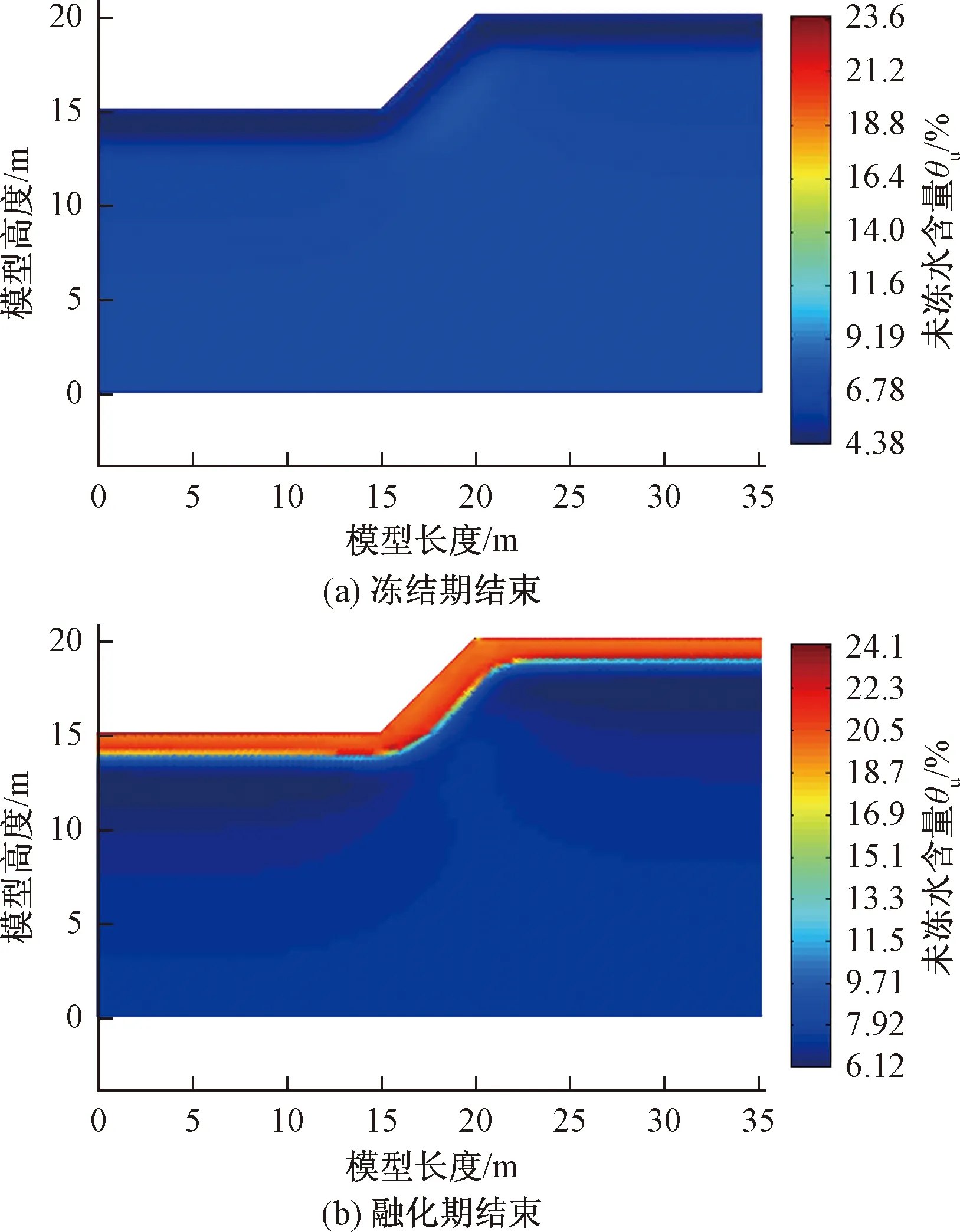
图10 不同时刻边坡的未冻水含量Fig.10 The unfrozen water of slope at different times
(3)冻融作用下边坡剪应力分析
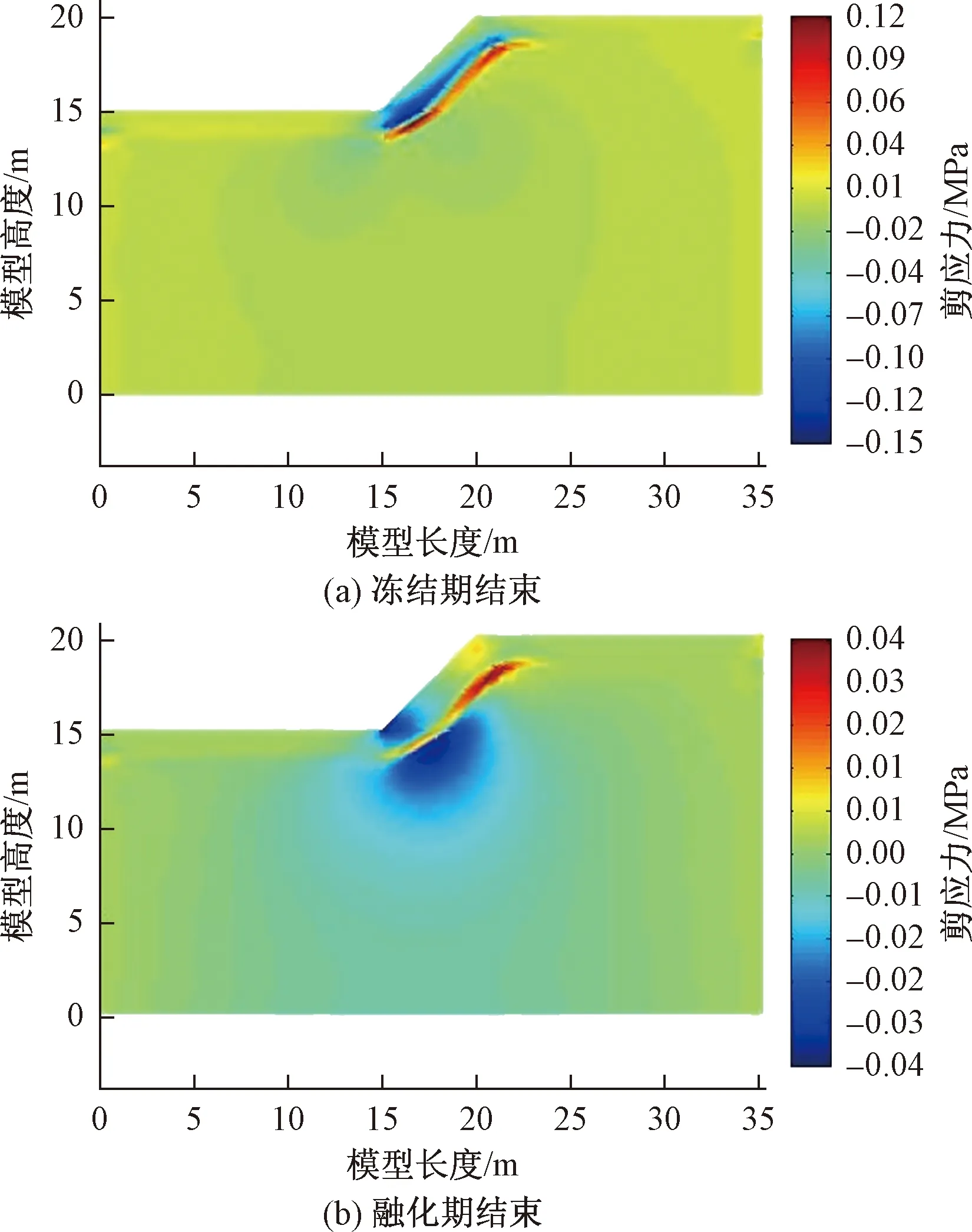
图11 不同时刻边坡剪应力云图Fig.11 The shear stress of slope at different times
由图11可知,无论冻结,还是融化结束时,坡体冻融交界面附近剪应力达到最大且呈带状分布,条带与坡面大致平行,但在坡顶和坡脚附近发生转折、小范围延伸而未贯通坡顶和坡脚,其余部分剪应力较小且分布均匀。冻结时坡面的剪应力大于融化时。原因在于:坡面上限以下土体常年处于冻结稳定状态,以上土体处于冻融交替状态,上限附近水分积聚,在自重作用下,坡面上限为冻土边坡潜在滑动面,故剪应力远大于其他部位。冻结时土体的弹性模量大于融化时,导致冻结时剪应力较大。
(4)冻融作用下边坡水平位移分析
由图12可知,冻结期结束时,坡面水平位移大小基本相同,中下部稍大,水平位移主要由土体冻胀引起;融化期结束时,边坡水平位移为上小、下大,呈“凸肚”状。边坡顶部受双向冻、融影响,顶部位移略大于顶部之下小范围土体的位移。冻结时边坡的水平位移比融化时小很多,原因在于:冻结时(即冬季),土体强度参数提高,且形成了冻结土骨架,主要为冻胀位移,坡体变形较小,稳定性较好;热融时(即暖季)土体强度参数降低,未冻水含量提高,边坡在自重和热融作用下稳定性降低,可能发生滑移,工程设计时应重视暖季热融失稳。
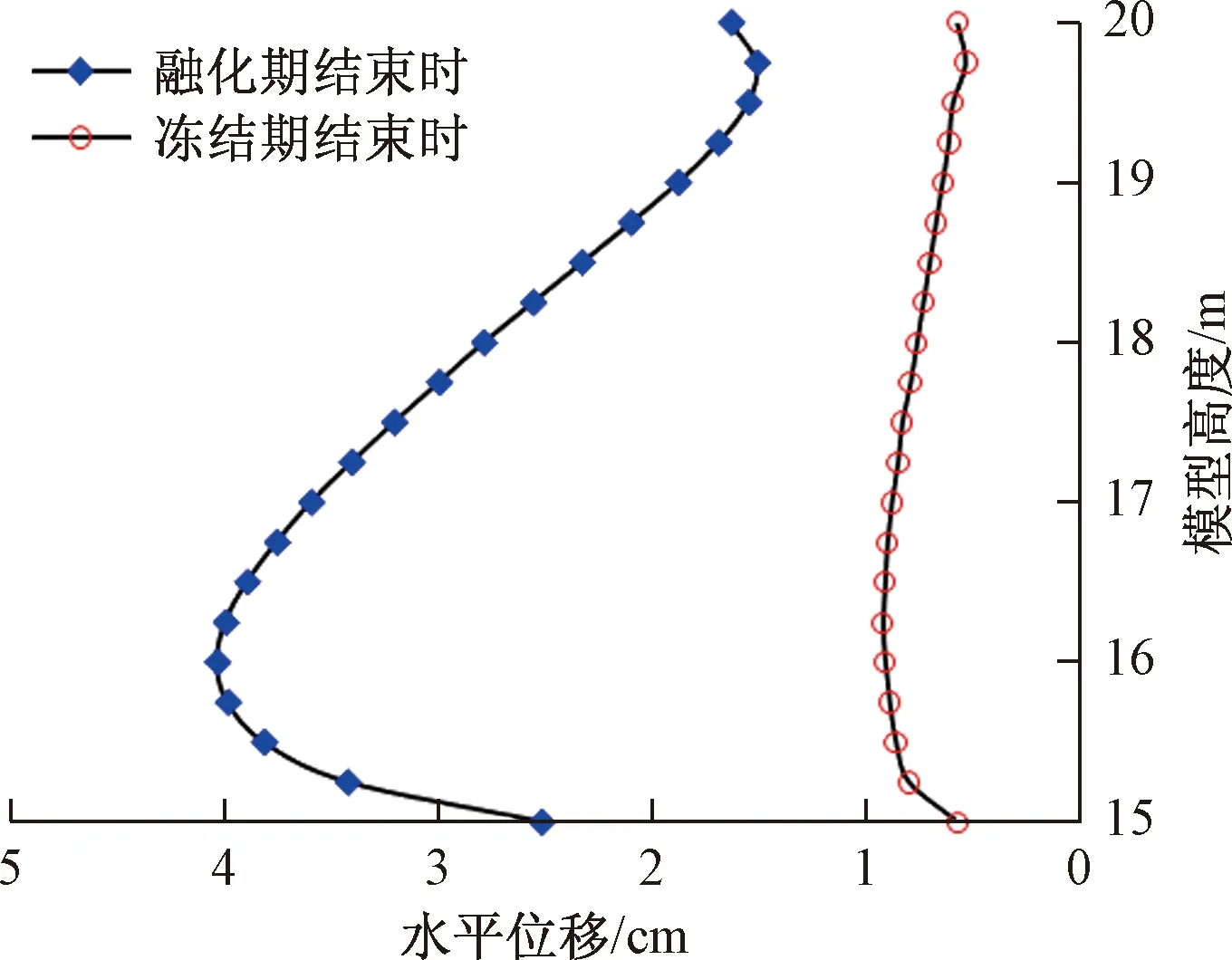
图12 不同时刻边坡水平位移Fig.12 Horizontal displacement of slope at different times
4 结论
(1)基于水热力耦合理论,依托MATLAB编制了能反应冻融作用下土体多场耦合机制的有限元程序,并与经典的PENNER[17]试验和MU等[18]模拟结果进行了对比分析,验证了程序的可靠性,开发了多年冻土边坡水热力耦合分析软件。
(2)冻融作用下边坡的活动层发生冻融交替变化,不同时刻冻土边坡温度场有明显差别,与坡面大致平行的冻融交界面出现剪应力最大条带。冻结期结束时,坡面水平位移大小基本相同,中下部稍大;融化结束时,边坡水平位移为上小、下大,呈“凸肚”状。融化结束时边坡的未冻水含量,水平位移比冻结时大,剪应力最大值比冻结时小;暖季多年冻土稳定性较差。
封面照片说明

