含石量和坡度对土石混合体崩塌运动规律的影响

成 浩，韩培锋,2，苏有文

(1.西南科技大学土木工程与建筑学院，四川 绵阳 621010; 2.水利部山洪地质灾害防治工程技术研究中心， 湖北 武汉 430010)

0 引言

土石混合体是由细粒土体、块石及孔隙构成的，且具有一定含石量的极端不均匀松散岩土介质系统[1]，是一种介于均质土体和破碎岩体之间的复杂地质混合堆积体[2]。土石混合体崩塌具有突发性、破坏力大、致灾范围广等特征，其运动形式复杂，给广大受灾山区的人民财产、交通运营及生态环境等造成巨大损失。我国14个集中连片贫困山区，已调查地质灾害及隐患点116 428处，其中崩塌18 827处，占比达16.17%，因崩塌地质灾害造成的贫困人口比例逐年增加，现已成为我国集中连片贫困山区扶贫和脱贫工作所面临的重要问题[3]。所以，研究土石混合体崩塌，对山区规划和发展具有十分重要的现实意义和社会价值。

目前，国内外学者对崩塌运动已开展了大量研究工作，主要采取现场试验、室内试验、数值模拟、理论分析四种研究方法。现场试验方面，黄润秋等[4-5]研究认为影响崩塌落石运动特征最主要的因素是坡度和坡面形态；GIANI等[6]研究发现崩塌落石形状越规则，其运动形式越复杂，运动距离越远。室内试验方面，OKURA等[7]研究发现花岗岩崩塌体的体积与落石运动距离成正相关；宋波等[8]研究发现落石形状的不同，其运动距离受远场地震作用影响较大。数值模拟方面，杨庆华等[9]采用二维颗粒流离散单元法模拟了崩塌过程，研究发现地震烈度越大，其崩塌规模越大、偏离临界坡脚越大、距离临界坡越远；黄小福等[10]运用非连续变形分析(DDA)法研究了地震荷载对危岩崩塌块体运动特性的影响。理论分析方面，裴向军等[11]研究发现滚石水平运动距离与坡度总体成正相关，块石运动形式有滑动、滚动、跳跃及其组合；贺凯等[12]基于影像资料，详细剖析塔状岩体的崩塌失稳过程。

综上研究成果对于崩塌的研究主要集中在落石的崩塌运动及运动特征，由于单体的岩石崩塌与坡面的接触面较小，其摩阻力相对较小，相应的运动速度较快、冲击力较大，所以对于单个物体容易造成严重的破坏。经过野外和文献调研发现，发生崩塌灾害的物源往往是土石混合状态的堆积体斜坡，而这些堆积体斜坡的坡度和含石量又各有差异；若斜坡在重力或外界条件作用下发生崩塌运动，那么含石量和坡度因素对其影响有多大，二者变化对崩塌运动又会产生何种效应规律，目前对于这两方面还鲜有研究。所以，本文基于野外典型崩塌灾害调研资料为根据，运用离散元素法构建不同计算条件下的土石混合体三维数值模型，探究其崩塌运动规律。旨在为山区道路交通建设、建筑物的选址和崩塌灾害防治提供参考依据。

1 崩塌区域概况及诱发原因

宝成铁路略阳至广元段，线路长132 km。本段位于龙门、大巴山区，沿嘉陵江上游的深切河谷下部行进，隔江与川陕公路并行。地理与气候方面：为龙门山边缘低山丘陵区，属大陆季风气候带，年降雨量800～1 200 mm，最大达1 900 mm。地形与地貌方面：嘉陵江是本区的最主要河流，近南北流向，区间线路在嘉陵江峡谷右岸；线路多位于陡坡陡崖下、高路堑或构造影响带内，最大切割高差约200 m，有好的临空面和坠落环境。地层岩性与地质构造方面：区间出露地层有志留系、二叠系、三叠系，在坡顶，坡脚广泛发育第四纪坡、崩积物，其中大小碎石含量约50%；本段地处龙门山褶皱带与大巴山褶皱带的复合过渡区，曾受多期次地壳运动和岩浆侵入影响，硬质岩层多，地层挤压强烈，断层节理发育，风化破碎严重[13-15]。所以，诱发崩塌的原因是，有利的地形地貌条件、复杂的地质构造，再加上降雨等外界条件的作用下，将会大大增加崩塌发生的概率和危害程度。

例如：2018年7月12—13日7时，受持续强降雨影响，宝成铁路略阳段王家沱站至乐素河站连续发生山体崩塌灾害，崩塌体约75 000 m3；其中上行线被掩埋线路约100 m，高约20 m，宽6 m，约4 000 m3；另外，除一部分堆积在坡面上，还有一部分越过铁路堆积在铁路下方至江滩间。截至7月13日10∶00，除了影响22趟列车的正常运营和生态破坏外，还给沿线居民生命和财产带来威胁。通过Google Earth Pro得到崩塌前的山体形态，崩塌前后对比(图1)。

2 三维离散元数值模型

2.1 离散元的基本原理

离散元素法(Discrete Element Method，DEM)最早由Cundall[16-18]教授首次提出应用于解决准静力或者动力条件下岩石力学运动问题。根据力与位移的关系，可以由位移得到颗粒受到的作用力，再由牛顿第二定律得出颗粒i的运动方程；利用欧拉法对式(1)两边同时积分，得到下一时间步长的更新速度；对式(2)两边进行积分，得到位移的更新表达式(3)；将该新位移代入力-位移关系计算新的作用力，如此循环反复，实时跟踪每个颗粒在任意时刻的运动[16](图2)。

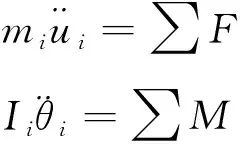
(1)

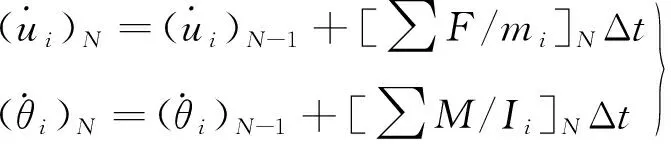
(2)

(3)

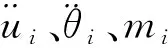
∑F、∑M——分别是颗粒在质心处受到的合外力和合外力距；

Δt——是时间步长；

N——对应时间t。

图2 颗粒运动计算示意图Fig.2 Calculation schematic diagram of particle movement

由上述颗粒运动求解过程可知，颗粒单元在相互作用过程中，颗粒形状、颗粒间及颗粒和滑槽间的作用点、时间步长等属性对模拟结果影响较大。由于颗粒表面的粘接力很小，故接触模型选用Hertz-Mindlin(no slip)(图3)。根据野外崩塌调研发现，块石并非是球形的，往往是有棱角的多面块体；所以，本文假定颗粒为有棱角形状的刚性体颗粒(图4)。为确保仿真计算稳定，时间步长设定为6.266 16×10-5s。

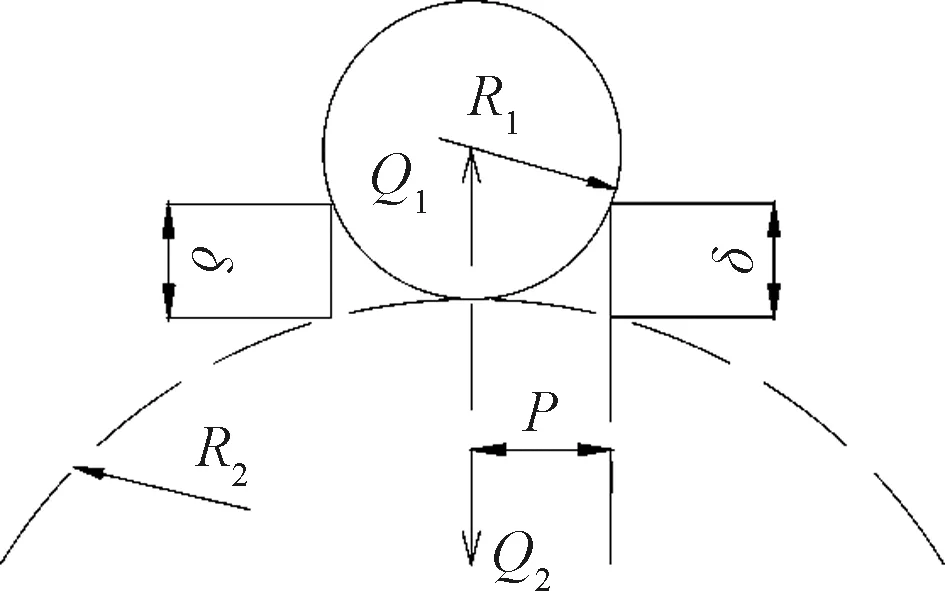
图3 颗粒接触模型示意图Fig.3 Schematic diagram of particle contact model

图4 单个块石颗粒组成大样图Fig.4 Detail of single rock particle

2.2 数值模型的建立

由于实际崩塌都有着十分复杂的地形，崩塌体的体量往往很大，且土石粒径组成极不均匀，这些因素都会限制离散元方法无法模拟现实的崩塌。根据前人研究经验,这类问题的物理试验研究一般利用滑槽进行，通过在滑槽的头部设置料箱，将土质颗粒或碎石放入其中；当料箱前缘挡板打开后，松散堆积体沿着滑槽向底部运动，以此来模拟滑坡、崩塌、泥石流的运动过程[19-20]；数值模拟的研究与此类似[21-23]。

因此本文基于相似比原理，合理简化模型，用滑槽模拟坡面地形，滑槽头部放置料箱模拟崩塌体，用坡脚底板模拟铁路及前缘区域；整个崩塌模型由料箱、崩塌体、滑槽和坡脚底板组成。在离散元软件EDEM中，数值模拟的整个过程主要有三部分；一是，设定模拟参数，导入崩塌模型，建立颗粒工厂生成颗粒，在重力作用下进入料箱形成崩塌体；二是，打开料箱前缘挡板，崩塌体在重力作用下发生崩塌运动，最后堆积在底板的过程；三是，模拟结果数据的在线分析、导出数据计算分析及崩塌过程的三维展示。滑槽几何尺寸：长1 800 mm，宽350 mm，高300 mm；料箱：长400 mm，宽350 mm，高200 mm；坡脚底板：长3 000 mm，宽2 000 mm，厚10 mm。颗粒密度2 100 kg/m3，颗粒总数51 247颗。图5为坡度65°崩塌模型示意图。试验材料颗粒级配表(表1)。

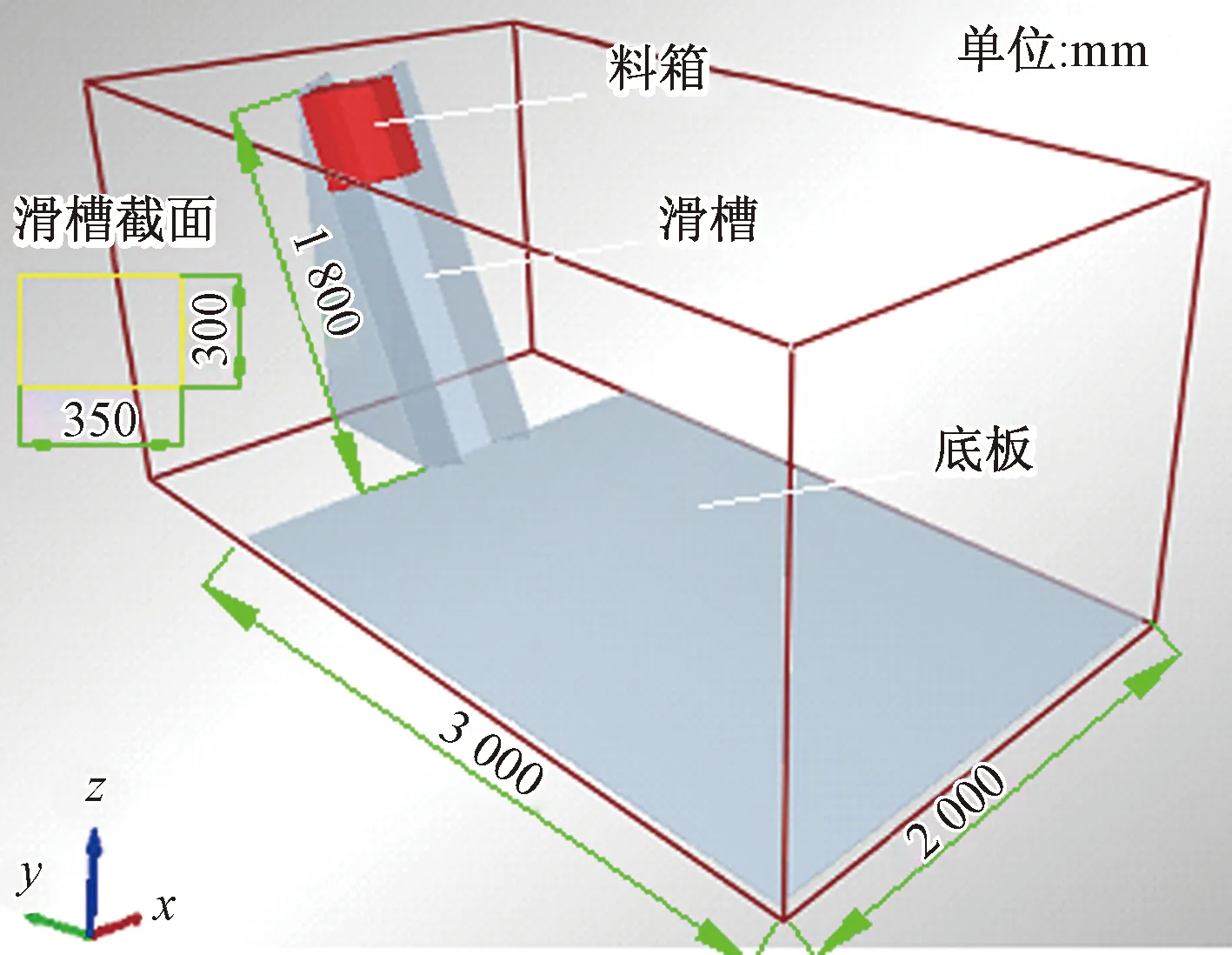
图5 崩塌模型示意图Fig.5 Sketch map of collapse

表1 试验材料颗粒级配表

2.3 数值模型计算参数的标定

基于野外调查选取典型土样开展土工试验，确定数值模拟颗粒材料特征参数以及弹性恢复系数，颗粒与滑槽间的静摩擦系数可以通过物理试验确定[24-25]。休止角是颗粒间流动特性和摩擦特性的宏观描述，是颗粒间静摩擦系数和滚动摩擦系数标定的常用指标[26-28]。因此，在前人对崩塌离散元的数值模拟参数标定基础上，以颗粒间的静摩擦系数、滚动摩擦系数作为试验因素，采用堆积法模拟休止角，经多次对比计算，以使模拟结果与实际崩塌运动相吻合，最终计算参数见表2、表3。

表2 材料属性表

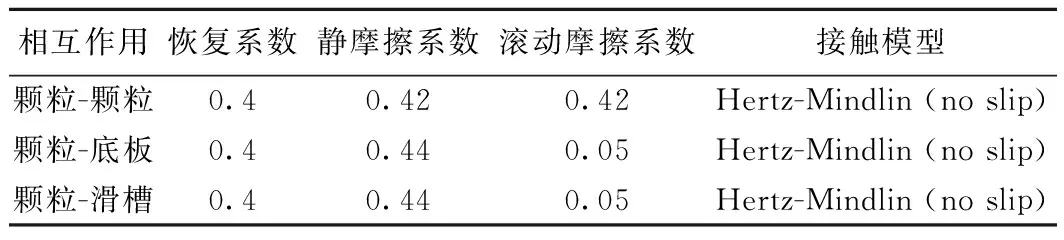
表3 接触属性表

2.4 崩塌试验方案

本次模拟试验设计不同计算条件下的崩塌运动，进而探究含石量和坡度变化对土石混合体崩塌运动规律的影响，方案见表4。

表4 崩塌试验方案

3 数值模拟结果与分析

3.1 土石混合体崩塌运动速度研究分析

3.1.1含石量对崩塌运动速度的影响

土石混合体中有细颗粒和大粒径块石，其在崩塌运动过程中速度各异，图6、图7为不同计算条件下细颗粒和块石平均运动速度的时程曲线。

由图6、图7可知，各种工况速度时程曲线的走势基本一致，均表现为速度加速上升阶段和速度下降阶段，而在两阶段临界点处出现速度峰值的时刻差异很小。其中，前者阶段为崩塌体从变形失稳至坡脚底板的运动过程，细颗粒和块石速度曲线差异不大；可能是因为滑槽设计的长度较短，速度还未区分就达到了速度峰值。后者阶段是崩塌体在底板上运动直到稳定堆积的过程，表现出含石量越大，细颗粒和块石速度下降越快，差异越明显；这是因为含石量越大，崩塌体自身摩擦力越大，底板对崩塌体摩阻力相应增大。

为研究含石量对崩塌体内部块石与细颗粒平均运动速度峰值的影响情况，得到图8。分析可知，块石与细颗粒曲线走势变化较平缓，无论含石量何种变化，平均速度峰值变化的趋势很小。这就说明含石量对崩塌体内部块石和细颗粒平均速度峰值影响较小。

图6 细颗粒平均运动速度时程曲线Fig.6 Time-history curve of average velocity of fine particles

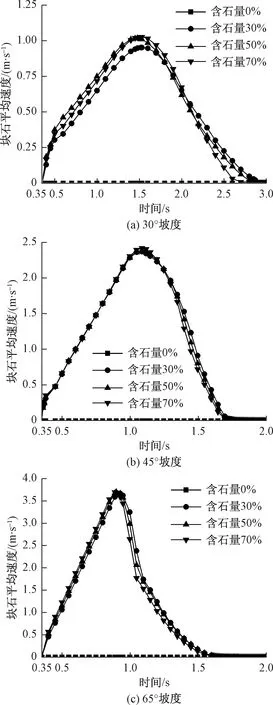
图7 块石平均运动速度时程曲线Fig.7 Time-history curve of average velocity of rocks

3.1.2坡度对崩塌运动速度的影响

图9、图10为不同坡度条件下各含石量崩塌体内部细颗粒和块石平均运动速度时程曲线。分析可知，各种工况速度曲线走势基本一致，均表现为速度上升达到峰值后速度下降。其中，坡度65°平均速度变化最为显著，坡度45°次之，坡度30°最小。从图中可以观察到，坡度越大，细颗粒和块石出现平均速度峰值的时刻越早。这是因为坡度越大，崩塌高度和崩塌体重力势能相应增大，使得崩塌体运动速度加快，速度变化更加剧烈。

为进一步研究坡度对崩塌体内部块石与细颗粒平均速度峰值的影响，得到图11。分析可知，细颗粒与块石平均速度峰值曲线走势基本一致，且随坡度增大而增大。从平均速度峰值斜率来看，坡度30°最小、65°次之、45°最大，可能是由于滑槽长度有限，崩塌体在达到坡度临界点后速度峰值增速开始减缓。这就说明坡度对崩塌体内部块石和细颗粒平均速度峰值影响显著。

崩塌运动过程中发现平均速度小于0.01 m/s时，崩塌运动基本停止，通过提取其崩塌时间数据以分析含石量与坡度变化对崩塌体运动总耗时的影响，如图12所示。图12(a)表明，崩塌体运动总耗时曲线随含石量的增大，呈逐渐减小的趋势，但这种趋势并不明显。其中，坡度30°曲线波动较大。原因是30°坡度较缓，崩塌体全由细颗粒组成，在运动中整体滑动性较好，所以运动时间相对较短；但随着块石含量的增大，相应的颗粒间摩擦和自身重力增大，从而影响崩塌体整体的滑动性。图12(b)表明，坡度越大，崩塌体从崩塌到堆积静止的总时间越短；表现为坡度30°时运动总耗时最长，坡度45°次之，坡度65°最短。当坡度由30°增大到45°时，总耗时降幅较大；而坡度从45°增大到65°时，总耗时降幅则较小；可能是因为崩塌体坡度在达到临界坡度前运动增速较快，则运动时间变化较大，而到达临界坡度后运动增速和总耗时变化差异较小。

图8 崩塌体内部平均速度峰值随含石量变化曲线Fig.8 Variation curve of average velocity peak value inside collapse body with rock content

图9 细颗粒平均运动速度时程曲线Fig.9 Time-history curve of average velocity of fine particles

图10 块石平均运动速度时程曲线Fig.10 Time-history curve of average velocity of rock

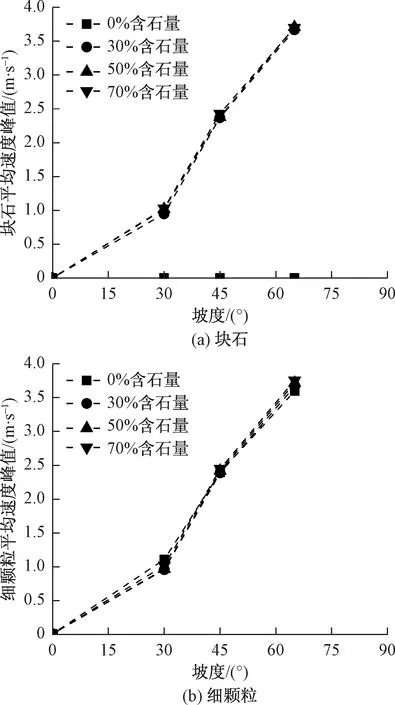
图11 崩塌体内部平均速度峰值随坡度变化曲线Fig.11 Variation curve of average velocity peak value inside collapse body with slope

综上图6～图12可知，细颗粒与块石平均速度均表现为速度加速上升阶段和速度下降阶段。同一坡度下，含石量对崩塌体内部块石和细颗粒平均速度峰值和出现峰值的时刻影响较小，平均速度曲线变化不明显；相同含石量时，坡度越大，速度峰值越大，出现平均速度峰值的时刻越早，速度变化越剧烈。所以坡度的变化对崩塌平均运动速度影响显著，应该重点关注。

3.2 土石混合体含石量和坡度对崩塌运动距离的影响

3.2.1含石量对崩塌运动距离的影响

图13为崩塌体和内部块石最大水平运距与含石量变化的关系。分析可知，崩塌体和块石曲线变化趋势大体一致，表现为含石量越大，曲线斜率越大，其运距越远。图14是以含石量0%的最大水平运距为基准，进一步研究含石量变化对最大水平运距增幅的影响；图中三类坡度增幅走势基本呈上升趋势，且含石量越大，其增幅逐渐增大，三条曲线逐渐分离。为探究崩塌体自身高度与最大水平运距之间的关系，得到图15；分析可知，当崩塌体自身高度越大，其最大水平运距越远，且含石量越大，曲线整体水平向右移动。这就说明含石量变化对崩塌运动距离影响较显著。

3.2.2坡度对崩塌运动距离的影响

图16表明，崩塌体与内部块石的最大水平运距曲线整体都呈现出上升趋势，且随坡度增大而增大。图17表明，最大水平运距增幅也表现出坡度越大增幅越大，坡度65°增幅最大、45°次之、30°最小。由图18可知，坡度增大的同时崩塌体自身高度变大，曲线整体向右上方向移动，其运距越远，三者成正相关。坡度影响崩塌运动距离的原因是，滑槽的长度是固定的，若坡度增大，势必崩塌高度增大，崩塌体的重力势能和重力加速度都变大，转化为更大的动能，所以运动距离越远。

为了使得崩塌体崩塌运动距离更具规律性和普适性，本文以运距比来评价水平运距与竖直运距之间的关系；其运距比定义为：崩塌体最大水平运距与最大竖直运距之间的比值。表5为最大运距比和平均运距比的计算结果。分析可知，含石量越大，最大运距比比值越大，平均运距比无明显变化趋势；坡度越大，其最大运距比和平均运距比都越小；这就说明崩塌高度越高，竖直运距就更接近水平运距。

综上图13～图18及表5可知，坡度一定时，含石量越大、崩塌体自身高度越大，使得其最大水平运距越远、最大运距比增大；相同含石量时，坡度越大，其崩塌体最大水平运距越远，最大运距比和平均运距比都越小。所以，含石量和坡度变化对崩塌地质灾害运动距离、危害范围影响很大，在对复杂地质山区土石混合体斜坡进行识别和监测时，应该重点关注此类崩塌体。

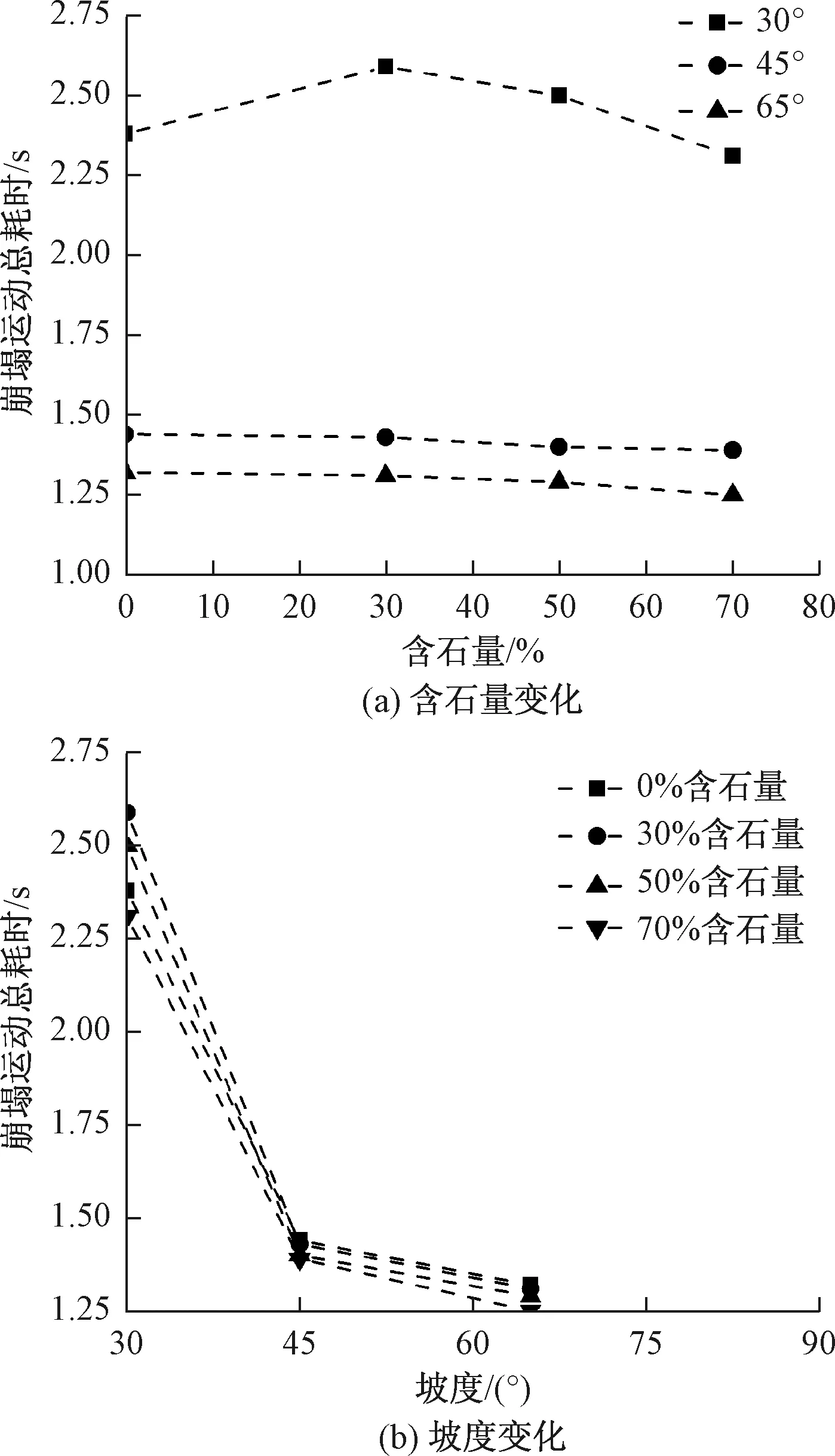
图12 崩塌运动总耗时随含石量和坡度变化曲线Fig.12 The total time of collapse varies with rock and slope

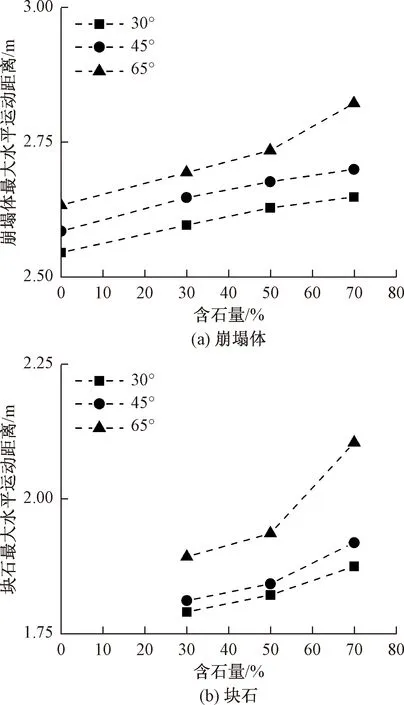
图13 最大水平运距随含石量变化曲线Fig.13 The variation of maximum horizontal movement distance with rock content

图14 最大水平运距增幅随含石量变化曲线Fig.14 The variation of the increase of maximum horizontal movement distance with the stone content

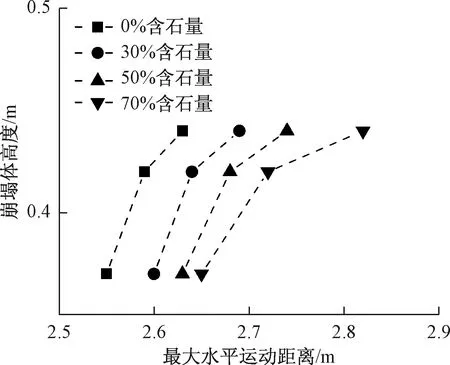
图15 最大水平运距随崩塌体高度变化曲线Fig.15 The variation of the maximum horizontal movement distance with the height of the collapse

3.3 土石混合体含石量和坡度对崩塌运动冲击力的影响

3.3.1含石量对崩塌运动冲击力的影响

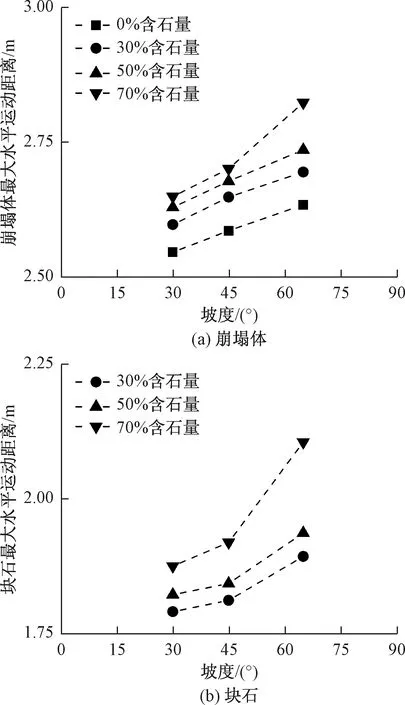
图16 最大水平运距随坡度变化Fig.16 The variation of maximum horizontal movement distance with slope

图17 最大水平运距增幅随坡度变化曲线Fig.17 The variation of the increase of maximum horizontal motion distance with the slope

通过提取各含石量崩塌体对滑槽和坡脚底板的接触合力，进而分析其冲击力的影响，得到图19。图19表明，同一坡度下，各含石量冲击力曲线走势基本一致。其中，图19(a)各含石量崩塌体整体以滑动为主，冲击力曲线波动很小；图19(b)崩塌体重力势能增大，冲击力表现较好，在运动时刻1～1.75 s对坡脚底板有明显的冲击，但冲击力不大。图19(c)可以观察到各含石量在整个崩塌运动中均出现明显的A、B、C三个冲击阶段分别对应滑动冲击阶段、动态冲击阶段和稳定堆积阶段。其中，滑动冲击阶段为0.35～0.88 s，冲击力曲线波动不大，是因为崩塌体快速倾塌对滑槽产生的撞击力很小。动态冲击阶段为0.88～1.16 s，冲击力曲线快速上升，达到峰值后快速下降；这是因为此刻崩塌体前缘开始冲击底板，后续颗粒接力补上位置继续冲击，当整个崩塌体都接触到坡底底板时，随着含石量的增大，依次出现冲击力峰值587.34 N、639.21 N、643.96 N、683.43 N，出现峰值的时刻分别为0.98 s、0.97 s、0.96 s、0.95 s；这就说明含石量越大，冲击力峰值越大，出现峰值的时间越早。第三个阶段崩塌体运动总能量完全耗散，表现为稳定堆积的过程。

3.3.2坡度对崩塌运动冲击力的影响

图20是不同坡度变化对崩塌体冲击力的影响情况。分析可知，相同含石量，不同坡度的冲击力曲线各有差异。其中，坡度65°冲击力曲线波动最大、坡度45°次之、坡度30°最小；坡度越大，冲击力峰值越大，出现冲击力峰值的时间越早。这是由于30°坡度较缓，其重力势能较小，各含石量崩塌体整体以滑动为主；45°坡度增大，其重力势能增大，冲击力表现较好；65°坡度陡峻，冲击力表现剧烈，不同时间段冲击力较为集中。

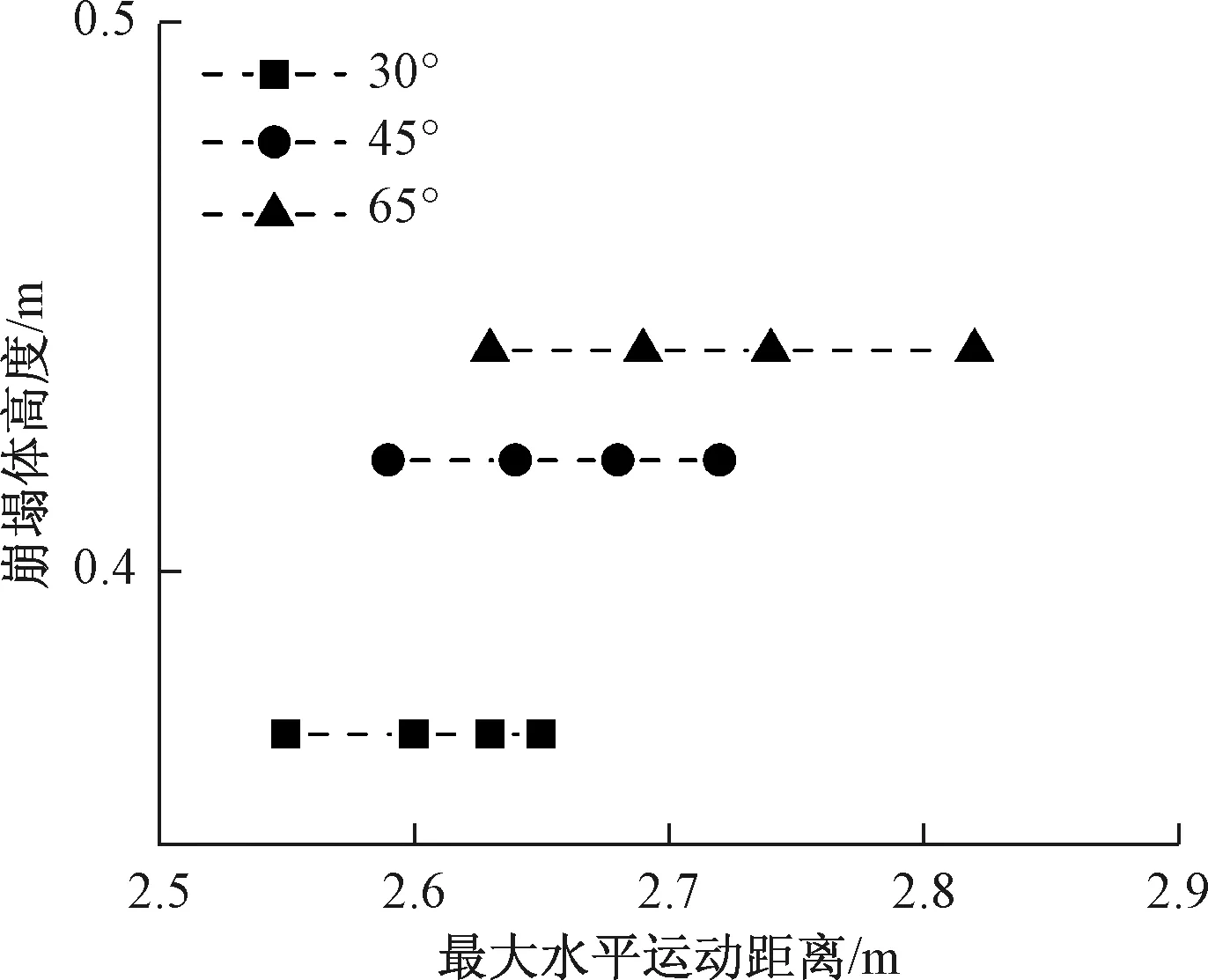
图18 最大水平运距随崩塌体高度变化曲线Fig.18 The variationof the maximum horizontal movement distance with the height of the collapse

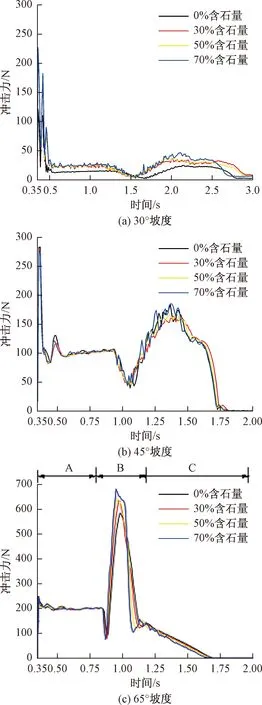
图19 不同含石量下冲击力时程曲线Fig.19 Time-history curves of impact force with different rock content

表5 崩塌体水平运距与竖直运距的关系

图20 不同坡度下冲击力时程曲线Fig.20 Time-history curves of impact force with different slope

3.4 含石量和坡度对土石混合体运动形式的影响

为研究土石混合体在实际崩塌运动中的特性，在前面的研究中发现坡度65°下含石量70% 崩塌体平均运动速度最大、最大水平运距最远、对底板冲击力最大。所以，有必要通过反演该崩塌体崩塌运动全过程进行分析研究。其中，块石为黄色颗粒，细颗粒为蓝色颗粒(图21)。

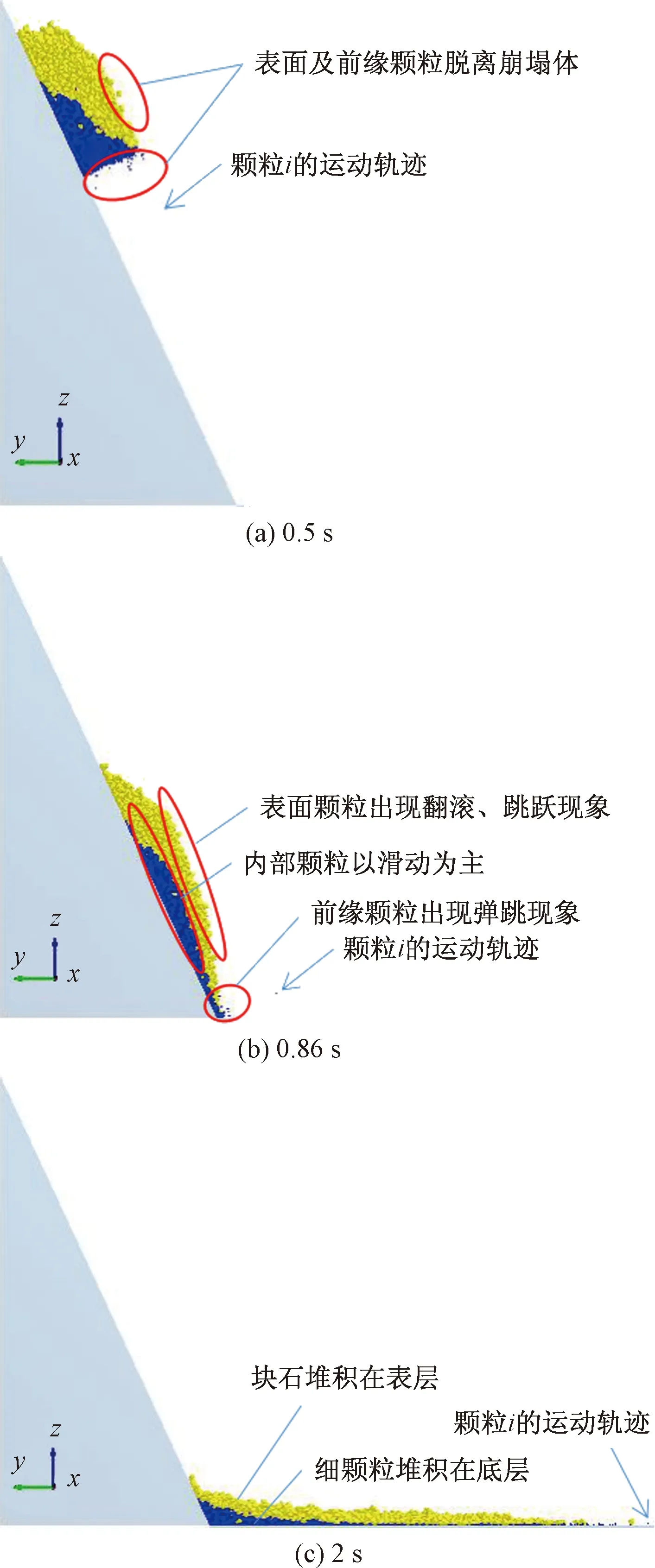
图21 坡度65°、70%含石量崩塌体崩塌运动演化过程Fig.21 The evolution process of the collapse movement with a slope of 65°and the rock content is 70%

当t=0.5 s时，位于前缘和表面的细颗粒与块石开始脱离崩塌体；这是因为崩塌体在重力作用下快速变形失稳，而前缘颗粒受约束很小，速度加持较快，后缘颗粒受前缘颗粒的阻挡加速缓慢，由此产生变形滑动。崩塌体在滑槽高速运动中，细颗粒与块石出现了翻滚、跳跃和滑动混杂的运动现象；块石向崩塌流表层运动的同时细颗粒相对向底层运动，可能是因为块石相较于细颗粒动能大，发生碰撞多，细颗粒顺着块石间的间隙下渗到底层，由此出现颗粒逆向分选效应。t=0.86 s时，前缘颗粒最先接触坡底，由于坡脚底板的阻挡而发生弹跳现象；此时，后缘颗粒接力补上前缘颗粒位置，形成长长的崩塌流。崩塌体受底板摩阻力影响较大，运动形式为减速滑滚，直至摩阻力大于其运动的力时，崩塌运动停止，t=2 s时为最终堆积形态。所以，该类崩塌体崩塌运动演化经历了变形滑动、高速滑滚、准静态堆积三个阶段，其运动形式有变形-滑动-翻滚-跳跃-堆积及组合，滑动在整个崩塌运动中为主要运动形式。

通过文献调研发现，本文模拟结果中的运动形式与苏学清对宝成铁路朝天至观音坝段崩塌现场研究所得出的运动形式[14]，以及一般的崩塌运动形式基本一致[4，11]；其中，从最终的颗粒堆积形态来看，模拟的细颗粒与块石存在颗粒逆向反序效应，这与实际的崩塌堆积中大部分块石位于表层或者被土颗粒包裹，如前文图1(b)所示。

由图22(a)可知，1.4 s时运动矢量的运动形式有两种情况：一是，由底面和后缘向表面和前缘运动；二是，堆积体后缘矢量先呈现出蓝色状态，且矢量速度不断下降。图22(b)为崩塌体1.27 s时的运动轨迹，可以观察到大部分颗粒单元的运动轨迹是连续变化的，呈现出流体性质，只有一小部分的红色流运动速度较快，脱离崩塌体；其中，在冲击底板的过程中离散性较大，这是因为崩塌体表面和前缘的颗粒受约束较小，在相互碰撞中出现翻滚、跳跃现象。

图22 坡度65°、70%含石量崩塌体崩塌运动图Fig.22 Collapse movement with a slope of 65°and rock content is 70%

4 结论

本文通过定量与定性结合的分析方法，探究含石量和坡度变化对土石混合体崩塌运动的影响规律，得出以下结论。

(1)细颗粒与块石平均速度均表现为速度加速上升阶段和速度下降阶段。平均速度峰值与坡度和含石量变化成正相关，出现速度峰值的时刻越早，崩塌运动时间越短。相同含石量时，坡度越大，平均速度峰值越大，出现平均速度峰值的时刻越早，速度变化越剧烈。

(2)坡度一定时，崩塌体含石量越大，其最大水平运距越远、最大运距比越大；相同含石量时，崩塌体坡度越大，其最大水平运距越远。

(3)冲击力峰值随坡度和含石量的增大而增大，达到峰值的时间越早；坡度65°时，各含石量在滑动冲击阶段和稳定堆积阶段无明显差异，动态冲击阶段冲击力波动强烈。

(4)崩塌体崩塌运动演化经历了变形滑动、高速滑滚、准静态堆积三个阶段，其运动形式有变形-滑动-翻滚-跳跃-稳定堆积。崩塌运动矢量和位移矢量前缘较后缘变化强烈；大部分颗粒单元的运动轨迹是连续变化的，呈现出流体性质，仅有一小部分的红色流速度较快，脱离崩塌流。