击打式松果采摘机器人设计与试验

王克奇 张维昊 罗 泽 张怡卓

(东北林业大学机电工程学院， 哈尔滨 150040)

0 引言

松果是一种成簇生长的林木球果，成熟后具有极高的营养价值和药用价值。松果采摘主要依赖人工，存在危险系数高、劳动强度大和采摘效率低等问题，不能满足行业发展需要，故实现松果机械化、自动化采摘具有重要意义。由于作业环境的非结构性和作业路径复杂等原因[1-3]，松果采摘机器人研究大多停留在实验室阶段。目前，簇生长果实机器人采摘主要采用吸附、抓取、剪断或折断等方式，可将其分为2类：第1类采用真空抽吸法使果实与果梗分离。如文献[4-5]研究了真空吸盘式果实采摘机器人，但松果表面不规则，不利于真空吸附。第2类通过夹持果实、切断或折断果梗使果实分离。如文献[6-8]提出旋拧方法实现猕猴桃和菠萝果实采摘，该方法采摘时易与相邻果实发生碰撞，且未讨论簇生猕猴桃的采摘问题。文献[9-11]对荔枝和番茄果梗切断特性进行研究，由于机械结构复杂，该方法不便深入植株内部采摘。松树高15～20 m、冠幅2～5 m，松果生长在松树树梢位置；松果果柄木质化程度高，果实分离力大；松果存在枝叶遮挡与重叠现象，这些都是研究松果采摘机器人的难题。

结合松果生长特征和针对现有采摘方式的不足，本文设计一种击打式松果采摘机器人。采用旋转击打的方式实现松果采摘，应用Matlab和ADAMS仿真对机械臂结构进行分析，探讨设计的合理性与实用性，应用ANSYS Workbench对结构进行优化设计，并求解结构安全系数与最大变形量，探讨设计的稳定性与有效性。

1 结构设计

1.1 总体结构设计

击打式松果采摘机器人由电机驱动模块、主控模块、视觉模块、夹持模块、采摘模块组成，其结构示意图如图1所示。

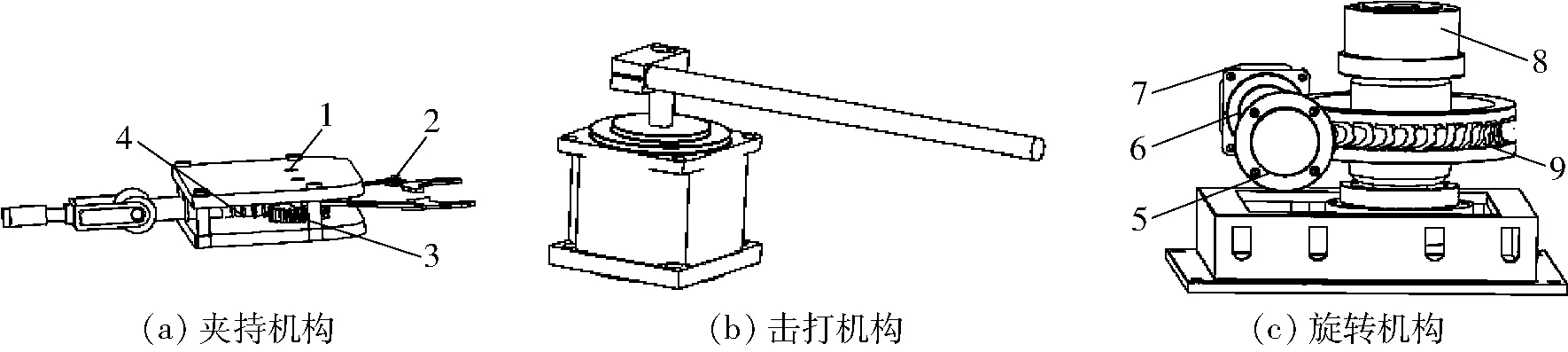
图2 关键组件结构简图Fig.2 Structural diagrams of important component1.夹持机械臂 2.夹持机械手 3.齿轮 4.齿条 5.轴承盖 6.蜗杆 7.步进电机 8.涡轮轴 9.涡轮

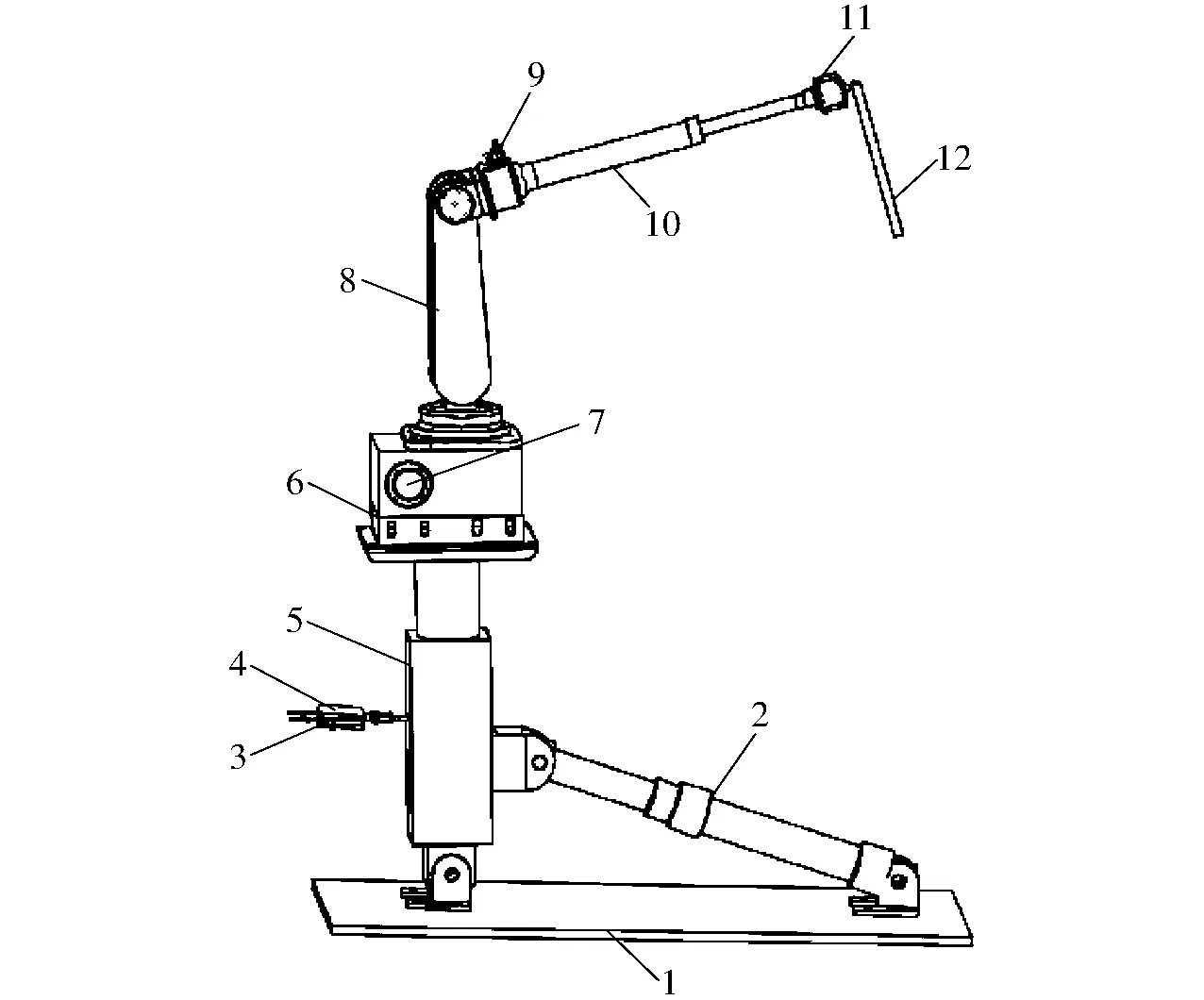
图1 击打式松果采摘机器人结构简图Fig.1 Structure diagram of hitting pine cone picking robot1.底座 2.支撑臂 3.夹持机构 4.传感器 5.升降臂杆 6.旋转机构 7.驱动模块 8.攀爬机械臂 9.视觉模块 10.采摘机械臂 11.步进电机 12.击打臂杆

松果采摘机器人通过视觉模块进行松果识别与定位，实时反馈给主控模块，并通过电机驱动模块控制夹持模块和采摘模块，由采摘模块的击打臂杆对松果所在树枝进行击打，实现松果采摘。驱动模块均采用步进电机(57BYG250H/86BYG250D型)进行闭环控制调节。设计松果采摘机器人过程中在满足强度和刚度要求的基础上，应满足最小质量要求，降低采摘工作的能量损耗。故松果采摘机器人的工作方式设计为：支撑臂伸长至升降臂杆与底座垂直位置，采摘机器人由初始状态转换为工作状态，夹持机构完成对松树主干的夹持，升降臂杆通过视觉模块捕捉松果高度信息进行升降，旋转机构和采摘机械臂根据松果位置信息进行调整，击打臂杆完成对松果所在目标树枝的击打。根据工作环境和实际要求，采摘机器人的夹持机构和击打臂杆在工作过程中会损伤树木的表面细胞组织，所以在与树干和树枝接触的位置采用软质橡胶进行包裹，以减小对树木表面组织的伤害。

1.2 关键组件设计

夹持模块由视觉传感器、夹持机械臂、夹持机械手以及连接件组成，如图2a所示。夹持机构在采摘工作中任务为夹持松树主干以保证采摘机器人在工作过程中的稳定性，起到夹持和平衡力矩的双重作用。考虑到夹持过程中应避免夹持机械手与枝条共面而导致夹持失败的情况，设计二自由度夹持机构，通过图像识别与处理保证夹持机构稳定夹持。

采摘模块由旋转机构、击打机构、视觉模块、传感器以及连接件组成。采摘模块通过涡轮蜗杆、齿轮传动和电机传动实现不同方向、小范围不同高度和不同距离松果的采摘。旋转机构采用涡轮蜗杆的传动方式可有效提高传动比，减小结构质量，其设计参数为模数5，减速比30，击打机构和旋转机构如图2b、2c所示；利用视觉传感器和激光范围传感器对松果进行双重识别与定位，实现采摘。

2 运动学仿真与分析

机器人运动学分析主要是末端执行器的位姿与机械臂关节变量之间的关系。采用D-H参数法建立击打式松果采摘机器人运动学方程，其连杆坐标系如图3所示，坐标系{O}为基坐标系。

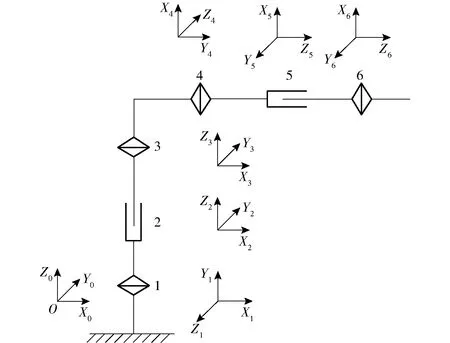
图3 机械臂连杆坐标系Fig.3 Link coordinate system of manipulator

2.1 正运动学求解

根据各连杆参数以及所建立坐标系的关系可得各关节的D-H参数，如表1所示。表中θ1、d2、θ3、θ4、d5和θ6为关节变量，αi、ai、di、θi分别为连杆扭转角、连杆长度、连杆偏移量、关节角。

表1 D-H参数Tab.1 Parameters of D-H

关节i(i=2，6)为移动关节变换矩阵

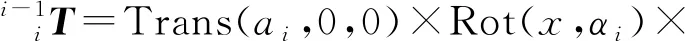
(1)

关节i(i=1，3，4，5)为旋转关节变换矩阵

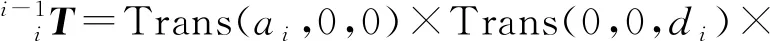
(2)

式中 Trans()——坐标系绕轴平移函数

Rot()——坐标系绕轴旋转函数

(3)

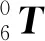
为简化书写，令cosθi=Ci，sinθi=Si，cosθicosθj=Cij，sinθisinθj=Sij，cosθicosθjcosθk=Cijk，sinθisinθjsinθk=Sijk。

位置向量p为

(4)

姿态矩阵为

(5)

其中

2.2 正运动学仿真与验证

基于Matlab平台Robotics Toolbox中改进型D-H参数法，根据表1数据设初始位置的机械臂姿态q0=(0°,400 mm,0°,0°,400 mm,0°),机械臂坐标轴为松果采摘机器人末端执行器位姿，则建立的机械臂模型如图4a所示。

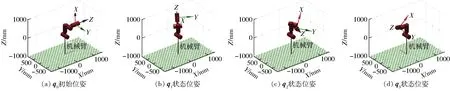
图4 机械臂位姿Fig.4 Position of manipulator

在机械臂各关节变量运动范围内，输入3组关节变量q1=(0°,400 mm,60°,-60°,400 mm,0°)，q2=(0°,500 mm,30°,45°,600 mm,0°)，q3=(0°,400 mm,90°,30°,400 mm,60°)，可得到机械臂位姿如图4b、4c、4d所示。为验证推导的正运动学方程的正确性和搭建模型的合理性，将关节变量q1、q2、q3分别代入式(3)。结果对比如表2所示。

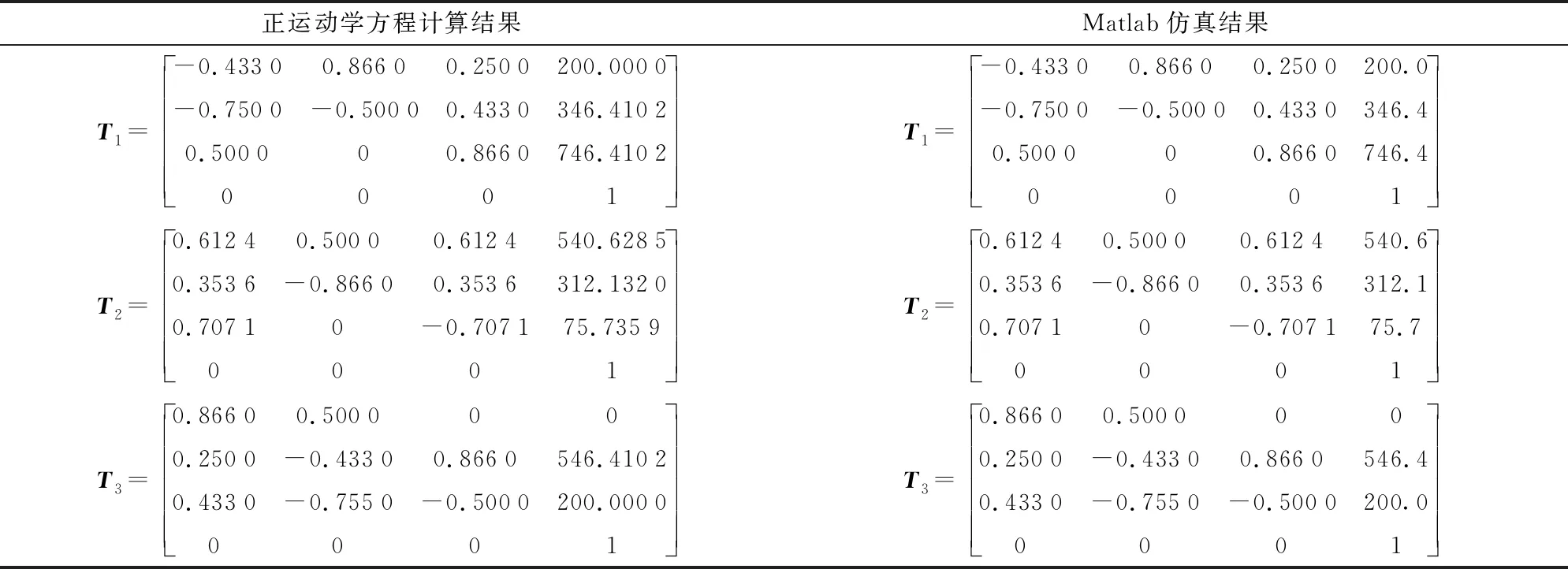
表2 结果对比Tab.2 Comparison of results

对比Matlab仿真结果和理论计算结果可知：输入相同的关节变量，输出的位姿是一致的，验证了正运动学模型及运动学方程的正确性。

2.3 逆运动学求解

运动学逆解用于机械臂末端执行器的精确定位和运动规划，其本质是将末端执行器的空间矢量信息转换为可供驱动电机识别的参数信息。逆运动学分析为已知机械臂末端执行器的位姿来求解各关节的关节变量，逆运动学的方法可以分为解析法、几何法和迭代法[12-14]。试验采用矩阵逆乘解析法求解运动学逆解

(6)

其中

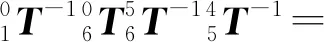
记(i,j)L为式(6)左边矩阵第i行第j列元素，(i,j)R为式(6)右边矩阵第i行第j列元素。根据式(6)，(3,4)L=(3,4)R、(3,3)L=(3,3)R，可得

(7)

由式(7)可得

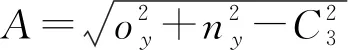
(8)

根据式(6)，(2,3)L=(2,3)R，可得

-C1C6oz+C6S1ox-S6C1nz+S1S6nx=0

(9)

化简式(9)可得

C1(C6oz+S6nz)-S1(C6ox+S6nx)=0

(10)

令

m=C6oz+S6nzn=C6ox+S6nx

则式(10)可改写为

mC1-nS1=0

(11)

由式(11)可得

(12)

根据式(6)，(1,4)L=(1,4)R、(2,4)L=(2,4)R、(2,1)L=(2,1)R，可得

(13)

由式(13)可得

其中

B=C6C1nz-C6S1nx-S6C1oz+S1S6ox

(14)

2.4 工作空间分析

工作空间是指机器人在采摘过程中，末端执行器所能达到空间点的集合，机械臂的工作空间是评价其完成任务能力的一个重要运动学指标。试验采用蒙特卡洛法[15-16]计算松果采摘机器人的工作空间。结合表1数据得到机械臂工作空间及XOY、XOZ、YOZ平面投影如图5所示。

由图5可知，机械臂工作空间连续、工作点分布密集，其形状可近似为直径4.5 m的球体，由于松果生长于松树树梢位置，其工作空间中心空洞为连接两关节连杆造成，采摘机器人位于松树0.5 m处，对比分析可知，理论求解空间满足实际采摘要求。

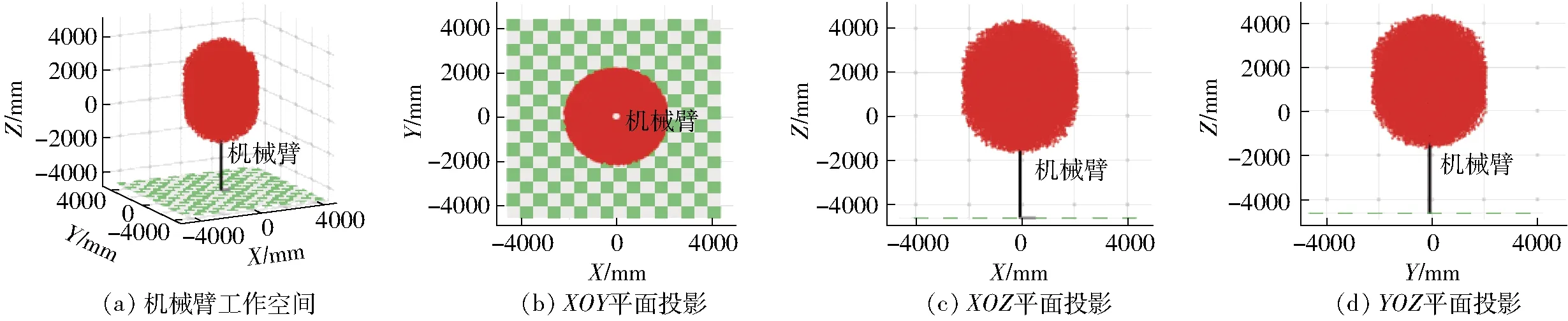
图5 机械臂工作空间Fig.5 Workspace of manipulator

3 动力学分析与采摘试验

3.1 动力学分析

机器人动力学是研究物体运动与作用力之间的关系，针对松果采摘机器人在目标捕捉和采摘过程的碰撞问题，采用第一类拉格朗日法[17-18]和冲量原理[19-21]建立机械臂的动力学方程和碰撞动力学模型。拉格朗日公式是一种基于能量的动力学方法，对于任何机械系统，拉格朗日方程为

L=Ek-Ep

(15)

式中L——拉格朗日函数

Ek——系统总动能，J

Ep——系统总势能，J

系统动力学带拉格朗日乘子的拉格朗日方程的能量形式为

(16)

式中qj——广义坐标，描述系统位形所需要的独立参数

λi——拉格朗日乘子

在ADAMS中建立虚拟样机模型，通过动态分析确定机器人的结构、响应时间等参数，完成对机器人动力学性能的评估。

动力学仿真模型如图6所示，碰撞发生瞬时各关节产生刚性冲击，碰撞后各机械臂运动状态和力学性能均发生变化，对机械臂运行过程中碰撞问题进行研究可为机械臂轨迹规划和实时控制提供理论依据。

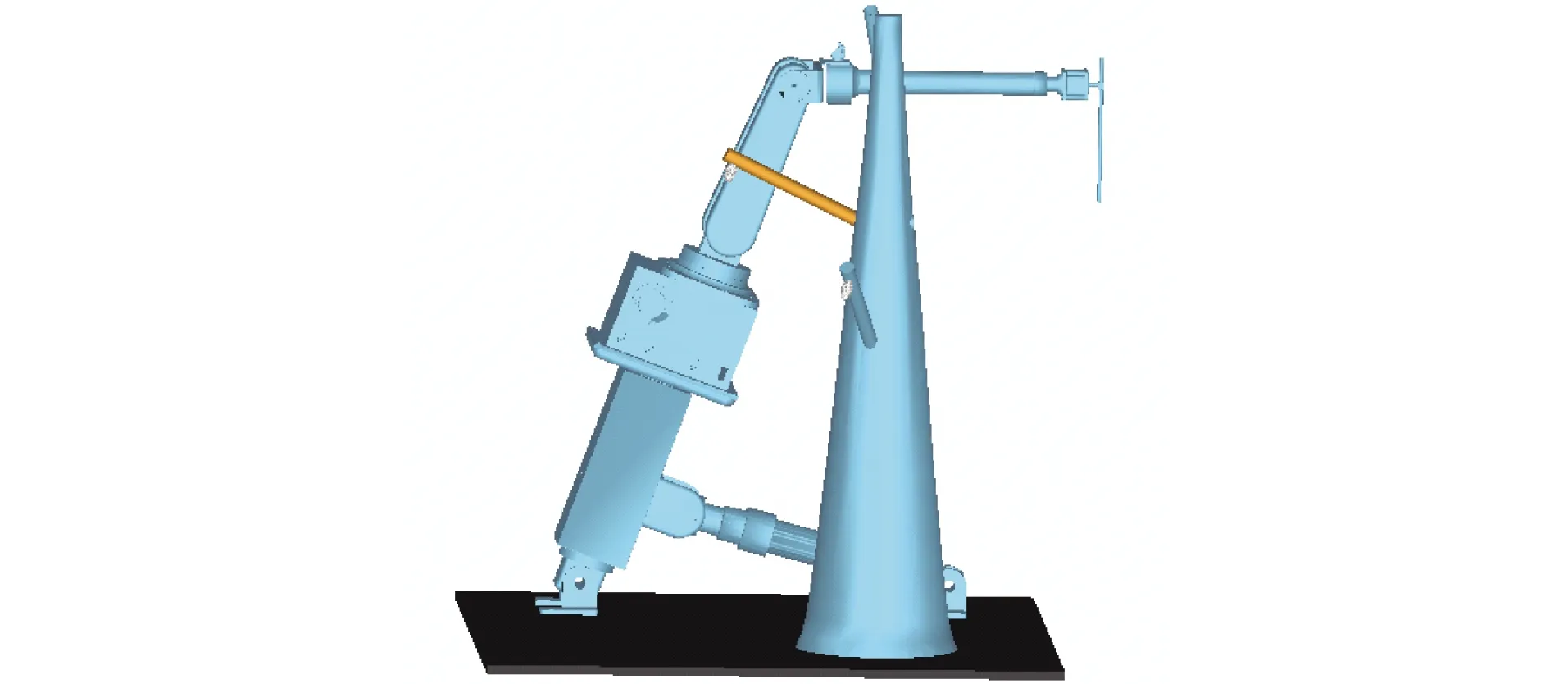
图6 动力学仿真模型Fig.6 Model of dynamics simulation

3.2 动力学仿真分析

ADAMS中设置仿真时间8 s，仿真步长500步，仿真方式为脚本仿真，重力加速度方向沿X轴正方向。根据经典碰撞理论[22]，假定系统碰撞接触时间无限小，碰撞是点接触，碰撞过程中杆的形状和惯量不变。设定松果采摘机器人击打臂杆在6.3 s第1次击打松果所在树枝，击打臂杆输入转矩3.6 N·m,输入转速500 r/min。试验结果如图7、8所示。

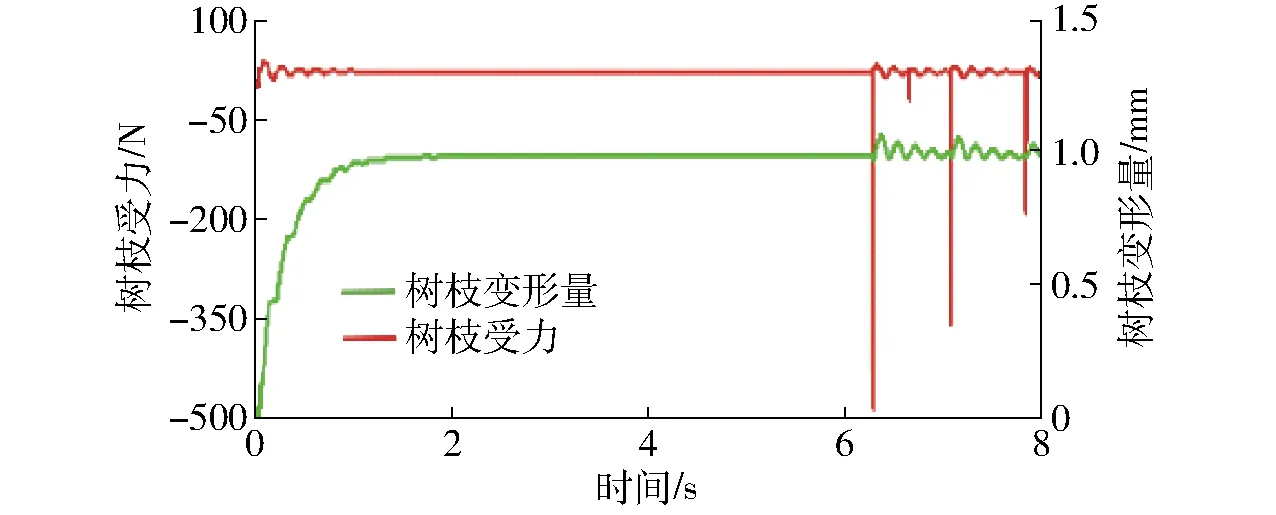
图7 树枝受力与位移曲线Fig.7 Curves of branch force and displacement

由图7可知，树枝在0～1 s内由于受到重力作用位移和力曲线均产生小范围波动；在6.3～8 s内受到机械臂多次击打产生位移和力的改变。通过受力分析可得到使松果掉落最小力矩。

由图8可知，机械臂受到冲击时导致系统速度突变，6.3～8 s机械臂与树枝产生3次碰撞，其碰撞发生瞬间各关节产生刚性冲击，t=6.3 s时产生第1次碰撞，其峰值转矩为1.2×105N·mm。若为保证机械臂碰撞后保持原有运动规律，需对各关节驱动力矩进行控制调节。

3.3 支撑关节静力学分析

支撑关节如图1所示，由支撑铰链和升降臂杆组成。松果采摘机器人的支撑关节在工作过程中不仅承受整个系统的重力和力矩，而且承受采摘过程中的交变载荷，是整个系统受力最为集中的关节，故对其进行静力学分析。由动力学仿真可知，支撑关节在6.3 s时受力最大，峰值6 400 N,利用ANSYS Workbench软件建立有限元分析模型，材料选择铝合金，如图9a所示。结构静力学用于计算在固定不变载荷作用下结构的效应，它不考虑惯性和阻尼的影响，静力分析方程为

Kx=F

(17)

图9 有限元分析Fig.9 Finite element analysis

式中K——刚度矩阵

x——位移矢量

F——静态加载节点力

极限载荷情况下，支撑关节最大变形量为4.148 4 mm，满足设计要求。

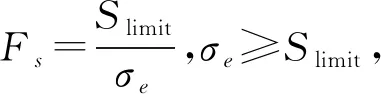
由图9c可知，应力集中区域出现在铰点处，安全系数最低为0.019 468，此处采用铝合金材料不能满足工作需要。故采用力学性能更好的镁合金作为支撑铰链材料，并采用双铰链和增加臂杆底座的方式对其进行加固，其仿真图像如图9d所示。其安全系数最低为1.577 1，可满足采摘需求。

3.4 松果采摘试验

图10 采摘试验Fig.10 Picking test

基于仿真结果，通过调整机械臂的尺寸参数、安装位置对结构进行优化，并搭建击打式松果采摘机器人样机，在实验室环境下进行松果采摘试验。仿真松树树高4 m，冠幅3 m，松果采摘机器人初始状态尺寸1 000 mm×1 200 mm×1 100 mm，质量45 kg，击打臂杆输入转速500 r/min。采摘试验如图10所示。姿态传感器(JY901型)实时监测机械臂运动位姿，并与理论位姿进行对比，利用控制系统负反馈调节可确保机械臂运动至指定位置。

试验表明：采摘时间22 min/棵，机械臂工作过程中角加速度曲线如图11所示。由图11可知，机械臂0～13 s运行平稳，各轴小范围波动是由于各机械臂运动所产生的耦合运动，击打臂杆13 s和35 s时分别击打松果所在树枝，导致角加速度发生突变，击打后机械臂恢复平稳运行状态，验证了机械臂具有较好的动态响应，其实际工作空间与理论分析基本一致。

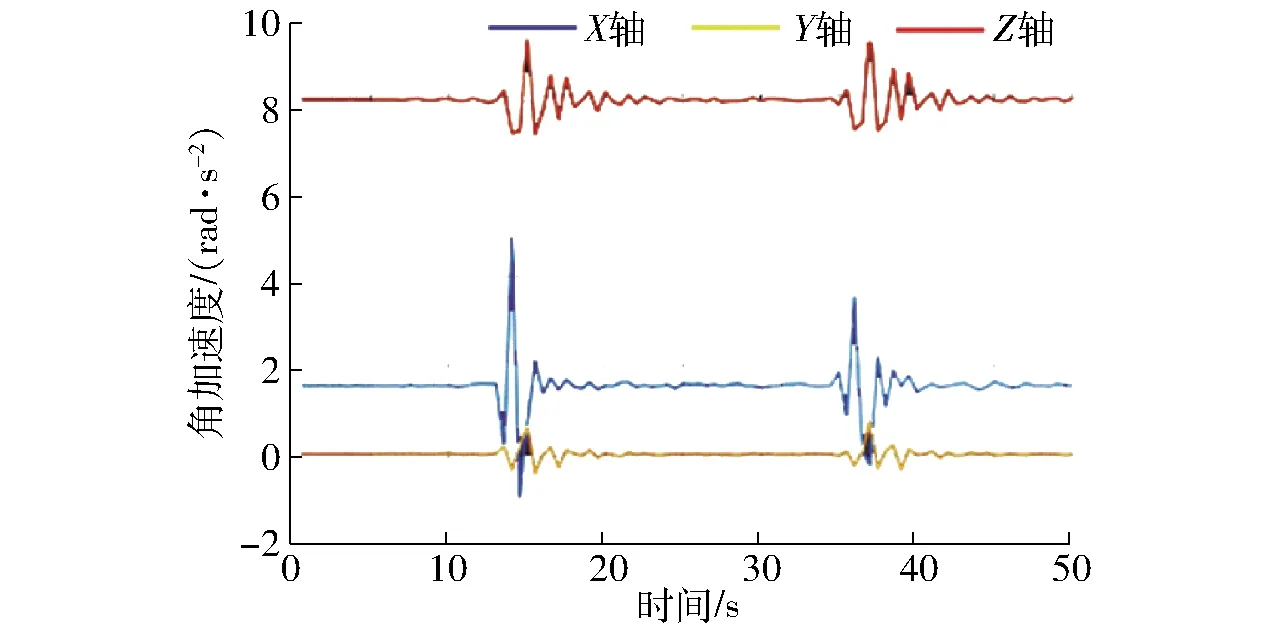
图11 角加速度曲线Fig.11 Angular acceleration curves

3.5 实用化分析

松树树高15～20 m，冠幅2～5 m，实际工作过程中各臂杆运动将产生较大惯性力矩和耦合运动，通过降低机械结构垂直方向的重心确保采摘过程运行平稳；由于击打臂杆在碰撞过程中产生较大扭转力矩，通过增加夹持机构和振动控制技术减小碰撞后机械结构的速度突变和抖动情况；林间树木间隔狭小、地势凹凸不平，通过视觉模块和激光范围传感器实现松果的准确识别和定位，采用高冗余自由度机械臂提高松果采摘机器人的避障能力。

人工红松林松果采摘过程中，将击打式松果采摘机器人安装于全地形履带车(SJ2000型，浙江省胜德电器有限公司)，用以适应复杂的林间环境，履带车由柴油机提供动力，采用远程操控的方式进行林间行走，行驶至目标树下，采摘机器人通过视觉模块进行松果识别与定位，机械臂通过主控模块自适应调整实现松果采摘。

4 结论

(1)设计了一种击打式松果采摘机器人，可实现在复杂林间环境下的精准采摘。其结构设计紧凑，可完成松果识别、定位和采摘等一系列工序。

(2)建立了采摘机器人运动学方程，基于Matlab Robotics Toolbox得出机械臂运动位姿，采用蒙特卡洛法求解出机械臂工作空间为直径4.5 m球体；基于ADAMS建立了碰撞动力学模型，分析得出采摘机器人最小击打力矩和碰撞后保持原有运动规律所需的驱动力矩，验证了结构设计的合理性与实用性。

(3)进行有限元分析，并搭建物理样机模型，运用ANSYS Workbench对受力集中组件进行安全系数和总变形分析，并对应力集中构件进行优化设计。结果表明：该机器人安全系数最低为1.577 1，支撑关节最大变形4.148 4 mm，应力分布合理；在实验室环境下进行了采摘试验，结果表明，其采摘空间、采摘过程树木受力情况与理论分析基本一致，验证了结构设计的稳定性与有效性。