非圆齿轮系大蒜直立移栽机构优化设计与试验

孙 伟 冯 江 蒋亦元

(1.东北农业大学工程学院， 哈尔滨 150030； 2.东北农业大学电气与信息学院， 哈尔滨 150030)

0 引言

根据我国大蒜的播种习惯和出口标准，要求蒜瓣鳞芽竖直朝上栽植。多位学者的研究表明[1-2]，鳞芽朝上的农艺栽植方式符合大蒜的生长特性，可以达到显著的增产效果。目前，我国大蒜种植主要依靠人工完成，其劳动强度大、生产效率低、生产成本高。发展大蒜机械化种植有利于专业化、标准化生产和管理，保证大蒜品质，提高国际竞争力[3]。

欧美国家较为成熟的大蒜栽植机械以非定向为主，且结构上多采用勺式取种，蒜瓣落地时方向完全随机。日本和韩国的代表产品为压穴式大蒜栽种机，依靠穴孔形状来控制鳞芽朝向，蒜瓣栽植后的直立度不易得到保证[4-5]。国外相关研究主要围绕蒜瓣的排种系统等关键部件展开[6-8]。国内已有的机械化大蒜播种机，播种时难以保证鳞芽直立向上入土，尚缺乏成熟的、满足国内大蒜种植农艺要求的播种机械产品，相关研究多集中于单粒取种和直立栽种环节。李玉华等[9]设计了一种轮勺式大蒜单粒取种装置，确定了取种勺及取种轮的最优结构。谢学虎等[10]设计了一种大蒜播种机的种植机构，并进行了初步试验研究。何岳平等[11]采用水稻插秧机分插机构的工作原理对大蒜栽植机栽植系统进行了运动仿真和分析，在理论上证明分插机构的优化参数符合大蒜栽植的农艺需求，但未见后续研究报道。

本研究以笔者团队在水稻和旱田移栽机等方面的研究成果为基础[12-16]，以非圆齿轮回转式移栽机构作为核心工作部件，设计一种大蒜机械化直立移栽机构。大蒜移栽机构的工作过程要求形成直线轨迹、保证末端操作器无转动，并同时满足其他多个目标要求，整个移栽过程中所形成的姿态和轨迹较已有的钵苗移栽[16-17]更为复杂。

1 数学模型

二阶非圆齿轮行星轮系大蒜直立移栽机构如图1所示，太阳轮与机架之间固定不动，太阳轮与中间轮、中间轮与行星轮之间均通过非圆齿轮副连接，且齿轮中心距相等，即a1=a2=a。中间轮转轴与行星架铰接，末端操作器与行星轮固接。机构由行星架提供动力输入，末端操作器在机构驱动下，形成移栽所需要的位置和姿态。

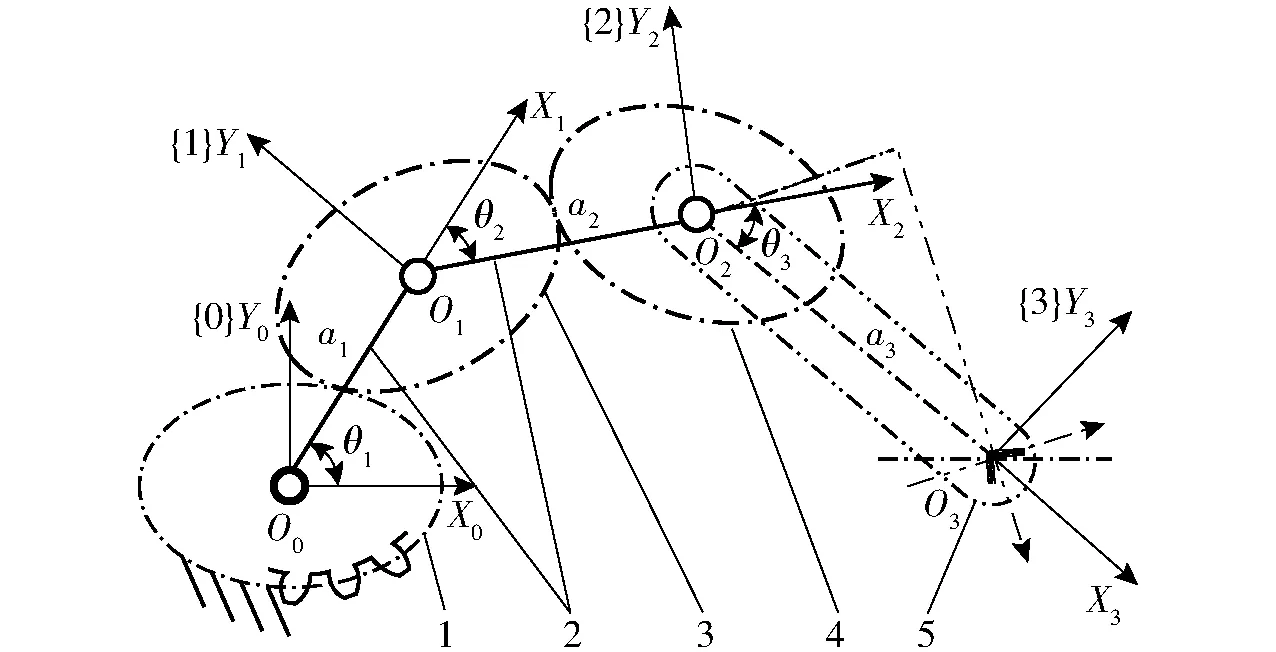
图1 大蒜移栽机构坐标系Fig.1 Coordinates of transplanting mechanism for garlic1.太阳轮 2.行星架 3.中间轮 4.行星轮 5.末端操作器

D-H变换方法是一种用于描述机构连杆间关系的建模方法，所用到的齐次变换矩阵是一个4×4方阵，它把一个矢量从一个坐标系转换到另一个坐标系，每一个矩阵可以同时实现平移和旋转两个作用[18]。通过用齐次坐标系表示原来的坐标矢量，就可以使用D-H变换来进行研究。因此，在非圆齿轮副上的每个适当位置建立一个坐标系，机构的空间运动问题即可转换为D-H变换问题。

为了研究大蒜移栽机构的末端操作器相对于太阳轮的位姿，首先在非圆齿轮行星轮系上以适当的方式建立坐标系。在图1中建立4个坐标系，用{0}、{1}、{2}、{3}分别表示固定坐标系(即太阳轮中心轴线坐标系)、中间轮动坐标系、行星轮动坐标系以及末端操作器动坐标系，Z0、Z1、Z2、Z3坐标轴的方向通过右手螺旋法则确定，图中未予示出。由此可以列出非圆齿轮传动行星轮系的运动学方程

T3=A1A2A3

(1)

式中T3——末端操作器动坐标系{3}的位姿矩阵

A1——中间轮动坐标系{1}相对于太阳轮动坐标系{0}的齐次变换矩阵

A2——行星轮动坐标系{2}相对于中间轮动坐标系{1}的齐次变换矩阵

A3——末端操作器动坐标系{3}相对于行星轮动坐标系{2}的齐次变换矩阵

每对非圆齿轮副可以由4个参数进行描述，如表1所示，表中S为未端操作器坐标原点与行星轮坐标原点之间距离。由于各旋转轴线相互平行，且为定中心距非圆齿轮传动，因此，在机构的运动过程中，齿轮转角随之改变，为变量，其他3个参数不变，为常量。

表1 非圆齿轮行星轮系坐标系参数Tab.1 Definition of coordinate parameters for planetary gear system with non-circular gears

各旋转算子和平移算子分别为Rot(Z0,θ1)、Rot(Z1,θ2)、Rot(Z2,θ3)、Trans(a,0,0)和Trans(S,0,0)，据此得到A1、A2、A3表达式

(2)

将式(2)代入式(1)，即可得到二阶非圆齿轮传动行星轮系运动学方程的完整表达式

(3)

式中n——末端操作器动坐标系法向矢量

o——末端操作器动坐标系姿态矢量

a——末端操作器动坐标系接近矢量

p——末端操作器动坐标系原点位置

太阳轮、中间轮与行星轮由优化后的传动比数值点序列qj(φ(j),i(j))(j=0,1,…,m)确定，利用三次非均匀B样条拟合方法进行计算[14,19]，qj决定传动比函数，插值点传动比为

ik=f(qj,φk) (j=0,1,…,m;k=0,1,…,l)

(4)

式中φk——插值点角度

ik——插值点传动比

l——插值点数

根据非圆齿轮的传动特性求得θ1、θ2、θ3之间的关系后，即可通过式(3)确定末端操作器在任意时刻的位置和姿态。

2 多目标参数优化

2.1 优化目标确定

2.1.1移栽轨迹分析

大蒜直立移栽机构需要与末端操作器相配合来完成直立栽植大蒜的动作，首先将大蒜种瓣从穴盘中取出，然后直立地栽植到土壤中。通过对人工栽植过程中所形成的理想栽植轨迹进行分析发现，手部与穴盘所形成的相对轨迹形如图2中所示的“δ”形。类似地，分析移栽机构所需要完成的移栽动作可知，首先要将末端操作器移动至大蒜穴盘处，并垂直从穴盘中夹取蒜瓣，如图中的轨迹1与2所示；随后将蒜瓣输送到地面附近，如图中的轨迹3所示；最后在地面处与末端操作器配合将蒜瓣推入土壤中完成栽植，如图中的轨迹4所示；移栽机构在回程时不能将已经栽植好的蒜瓣推倒，如图中的轨迹5所示。

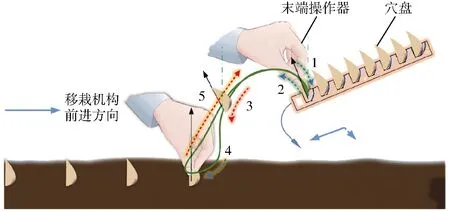
图2 大蒜移栽轨迹分析Fig.2 Analysis of trajectory for garlic transplanting

2.1.2优化目标分析

由以上分析可知，大蒜直立移栽机构涉及高维多目标优化问题，其结构形式、机理研究和优化与已有研究成果相比难度更高。在结合文献[3]和研究团队前期探索性成果的基础上[16-17]，提出大蒜直立移栽机构的优化目标如表2所示。

根据优化目标的性质，可以将其分为3个类别：“干涉检查”类目标、“生物对象”类目标和“机械性能”类目标。“干涉检查”类目标包括移栽机构与穴盘装置距离、齿轮箱与地面距离和穴盘装置与地面距离3个目标；“生物对象”类目标包括末端操作器尖嘴宽度、末端操作器尖嘴倾角、入穴段末端操作器摆角、出穴段末端操作器摆角、取蒜入程角、栽蒜角、栽植摆角7个目标；“机械性能”类目标包括齿轮模数和轨迹高度2个目标。

表2 中的12个优化目标都不是一个确定数值，而是模糊的，一般认为在给定范围内的数值都是合适的。另外，各个目标之间存在交互关联性，某一个目标的改变，可能会影响其他几个目标值的变化，各个目标改变的关系也有强烈的非线性。根据各个优化目标的性质和目标要求，确定移栽机构的多目标规划数学模型

表2 大蒜直立移栽机构的优化目标Tab.2 Optimization goals of vertically transplanting mechanism for garlic

(5)

2.2 多目标优化实现方法

2.2.1GUI多目标优化软件设计

多目标优化问题的求解方法很多，大体上可以分为两类：直接求出非劣解，然后从中选择较好的解；将多目标优化问题做适当的处理，如进行加权处理等。这些求解方法在优化目标不太多时可以得到满意的结果，但对于本文所涉及的具有模糊性、非线性和强耦合性特征的问题则难以解决。为此，赵匀等[20-21]基于人机交互优化的思想，提出了“参数导引”启发式优化算法。优化算法的本质是目标函数向量逐次逼近期望值向量的过程，直到各目标计算值与期望值的差值满足所允许的最大偏差值向量要求后，所得到的参数即为非劣解参数。一般而言，可以得到由多组非劣解参数所构成的非劣解群，进一步地，再用其他评价方法来对非劣解群当中的参数进行比较，从中选择最终的设计参数。

采用参数导引启发式优化算法的思想，基于Matlab平台编写了大蒜直立移栽机构的GUI多目标优化软件，软件界面如图3所示，主界面主要由优化目标区、参数输入区、图形显示区、计算仿真区和优化结果区组成。

优化目标区：在机构优化目标显示区，将所设计的运动学目标，按照目标的重要程度，将最重要的目标排在最上方，次要的目标依次向下排列。通过该模块实时地显示当前机构参数下目标的优劣，红色进度条越长意味着目标越优异，黑色进度条则表明目标不合格。

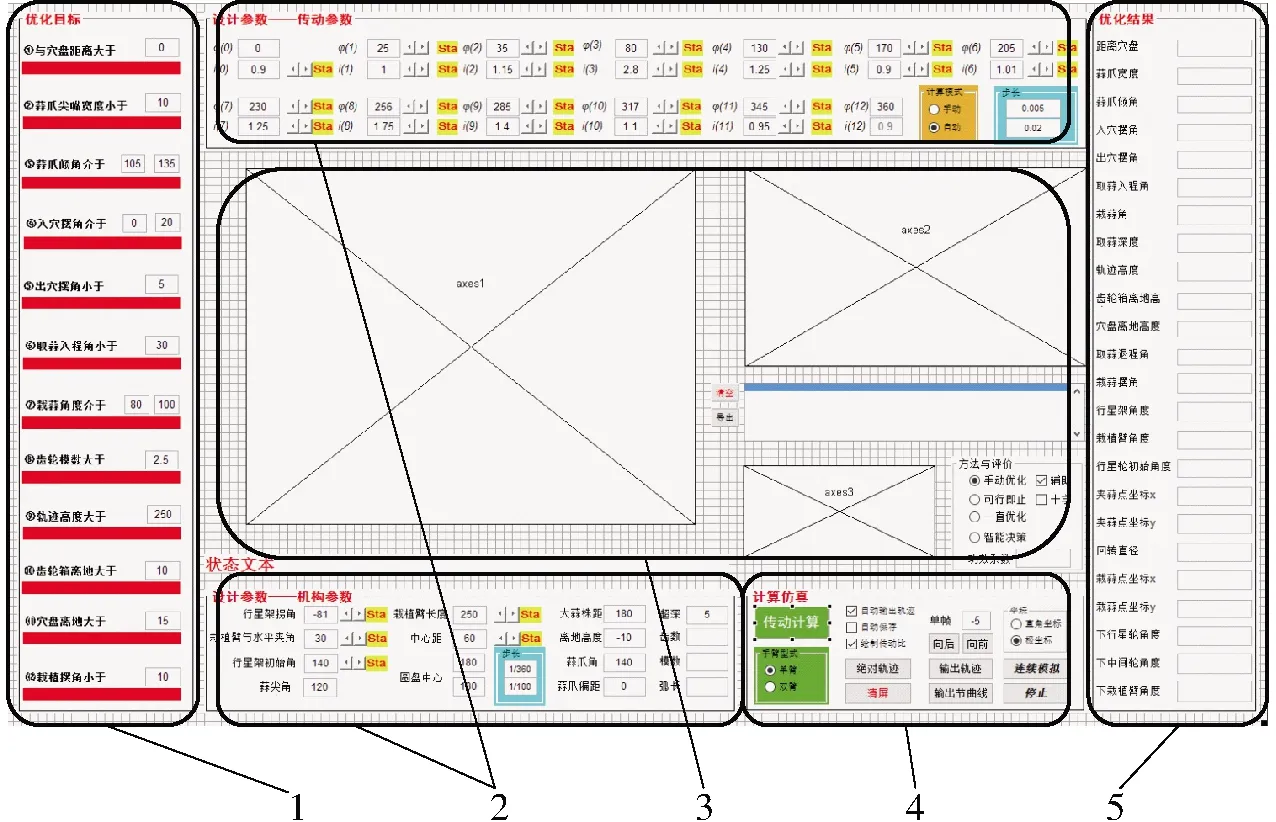
图3 非圆齿轮系大蒜移栽机构GUI优化软件界面Fig.3 GUI optimization platform of vertically transplanting mechanism for garlic1.优化目标区 2.参数输入区 3.图形显示区 4.计算仿真区 5.优化结果区

参数输入区：包括两部分，即机构参数和传动参数。机构参数输入部分主要包括行星轮系的各种长度尺寸和角度尺寸，可步进调整的有5个，传动参数部分为所定义的13个型值点，其中每个型值点对应角度和传动比两个参数，并且首尾点重合。

图形显示区：用于显示机构的运动学状态，包括非圆齿轮系的啮合状态、相对运动轨迹和绝对运动轨迹、传动比曲线等。

计算仿真区：用于进行机构的运动学计算和运动仿真分析，可以进行连续模拟或步进模拟，可以将机构的轨迹和齿轮的节线参数输出为数字化设计软件可读的格式，从而方便数据交换。

优化结果(输出)区：显示重要的目标值和机构位置参数，是进行机构设计的重要参考依据。

2.2.2优化流程与结果

参数导引优化算法的思路是根据目标的重要程度依次逐步逼近，使得所有目标满足要求，使用软件进行交互优化时按照图4所示的流程进行。

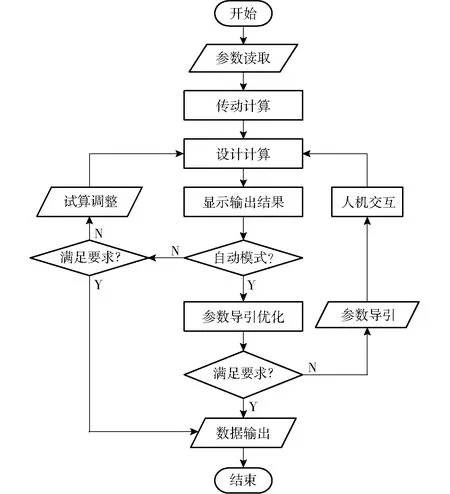
图4 优化流程图Fig.4 Block diagram of optimization process

当使用软件进行机构优化时，可以通过参数输入模块输入一组初始化参数，也可以从计算机硬盘中读取已经存档的参数。单击计算仿真模块中“传动计算”命令按钮，当采用手动计算模式时，系统将等待用户操作，而不自行激活参数导引启发式优化算法程序，用户可以根据设计经验自行调整参数，主要用于优化前期的试验计算。当采用自动计算模式时，将激活参数导引启发式优化算法程序，此时将会在所有目标当中自动寻找不符合要求的目标，在需要调整的参数后面出现“≪”或“≫”调整符号，表明程序通过参数导引启发式优化算法的计算判别后，使该参数“减小”或“增大”能够使目标得到最速的优化。计算完成后，用户通过图形显示区观察机构的初始状态和第一级非圆齿轮的传动比函数曲线。通过观察优化目标区进度条的形态，将显示为黑色的不合格目标作为最差目标进行优化。待得到满足要求的机构参数后，利用运动仿真功能对机构进行再次检查，判断机构的虚拟运动状态，初步检验设计的正确性。

从不同的初始参数出发时，所获得的优化结果一般并不相同。实践当中所采用的方法是，在满足约束条件的区间内采用多组初始参数集，以此为基础进行优化，再从获得的非劣解群中选定最终的机构参数。经过最终优化，选择了一组各方面指标较为权衡的最优解，如表3 所示，在该组最优解下的优化目标结果如表4所示。

3 参数化设计

3.1 非圆齿轮成型

经过多目标优化后，导出非圆齿轮节线数据，并将其输入到KissSoft软件中进行非圆齿轮生成。对齿轮结构参数进行优选，并对非圆齿轮啮合关系进行模拟啮合测试，获得满意的齿形轮廓后，在CATIA中进行非圆齿轮的三维实体建模。所选的非圆齿轮具体参数如表5所示，所生成的非圆齿轮实体模型如图5所示。由于行星轮与太阳轮的齿轮节线参数完全相同，图中只列出了太阳轮和中间轮的实体模型。

3.2 机构设计与验证

移栽机构的设计与验证过程如图6所示。在CATIA软件中，以多目标优化获得的结构参数为依据，采用“自上而下”的设计方法[22-23]进行移栽机构的详细设计。将移栽机构的零部件按功能与类型逐层分解，形成具有继承关系树状结构的谱系层次。基于已经生成的非圆齿轮零部件，在装配设计工作台中以一个产品文件为基础建立骨架，然后在该产品文件中建立所有零部件。当末端操作器运动至移栽轨迹的关键位置后，根据移栽轨迹与穴盘、地面的位置关系，选取开始取蒜时刻、结束取蒜时刻、开始栽蒜时刻、结束栽蒜时刻4个时刻，确定末端操作器凸轮的4个分界点，以实现取蒜、带蒜、栽蒜和回位4个过程。采用自上而下的设计方法时，移栽机构的重要特征可以在装配体下完成，从而使各个特征修改时能够准确定位。

表3 多目标优化参数取值Tab.3 Multi-objective optimization parameter values

表4 多目标优化结果Tab.4 Multi-objective optimization results

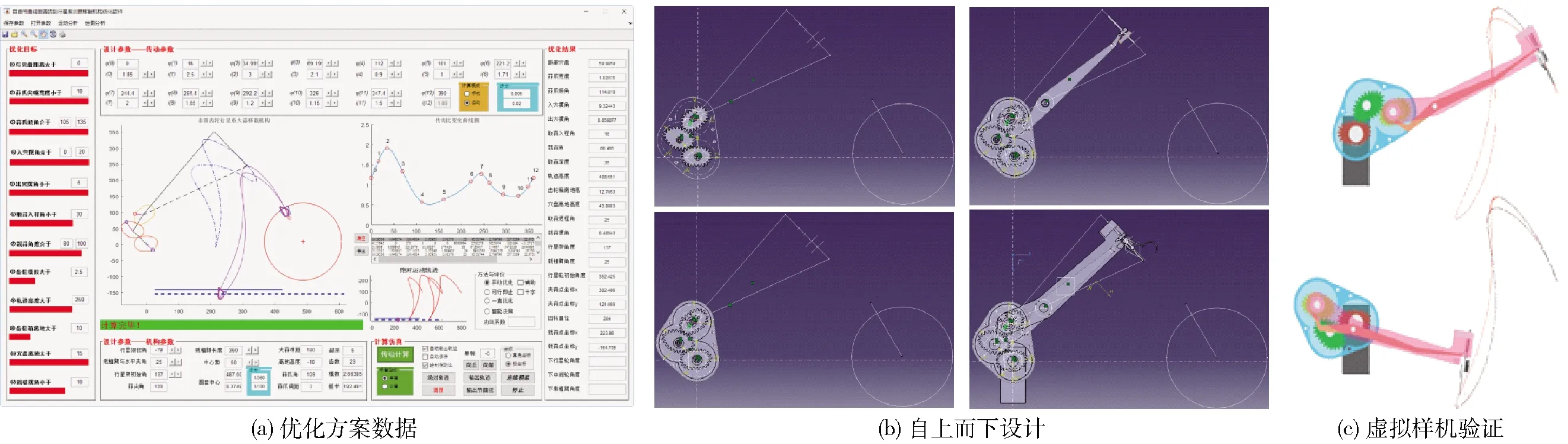
图6 移栽机构设计与验证Fig.6 Design and verification of transplanting mechanism

表5 非圆齿轮结构参数Tab.5 Structural parameters of non-circular gear

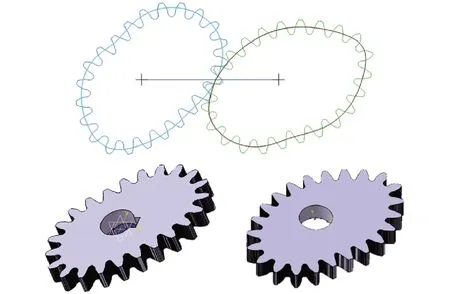
图5 非圆齿轮实体模型Fig.5 Solid model of non-circular gears

在CATIA中完成移栽机构的参数化设计后，将模型导入到ADAMS软件中，按照机构的运动原理来添加约束与驱动进行虚拟样机验证。理论移栽轨迹和虚拟样机所获得移栽轨迹如图7所示。观察移栽机构的工作轨迹可知，栽植段轨迹1和夹取段轨迹2均表现出较好的一致性。虽然虚拟样机获得的移栽轨迹显示出略微的抖动，但其在关键位置的稳定性较好。由于在非圆齿轮的啮合表面采用了接触约束，会产生微量的啮合变形，因而会产生抖动。图中抖动较为明显的一段发生在转折段轨迹3，包括去程和回程在内的两段均产生了较其余轨迹大的抖动现象。其可能原因是在转折段3的非圆齿轮啮合位置发生反向回程间隙，加之在转折处机构的惯性力较大所致。由于此处位置离栽植段1和夹取段2较远，并不在关键工作位置上，只要末端操作器工作可靠，不会对移栽工作产生影响。经虚拟样机验证，实际轨迹、姿态与设计初衷相符，说明设计参数可靠，设计步骤无误。

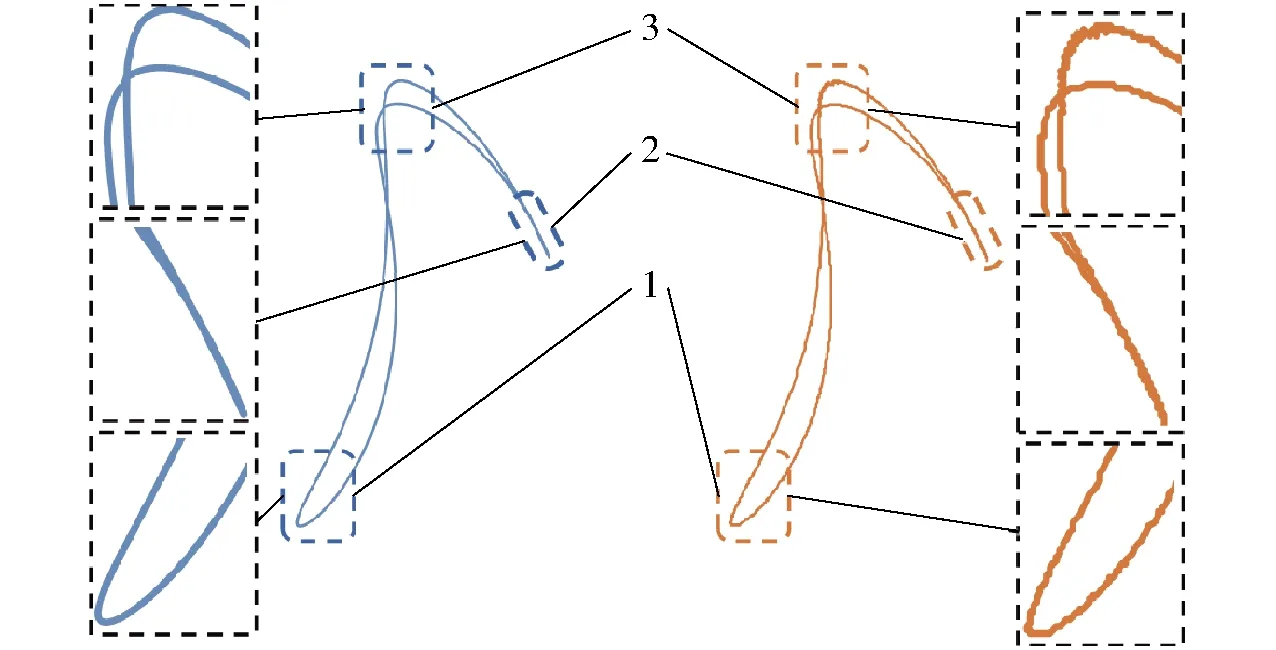
图7 移栽轨迹对比Fig.7 Comparison of transplanting trajectories1.栽植段轨迹 2.夹取段轨迹 3.转折段轨迹

4 台架试验

4.1 试验装置

大蒜直立移栽机构试验装置如图8所示。移栽机构在电机1的驱动下执行移栽动作，传送带由电机2驱动，土槽在传送带的带动下与移栽机构形成相对运动，穴盘的位置可以通过标尺进行微调。试验所用计量仪器主要包括伺服电机调速器、角度仪、测速计、游标卡尺等。

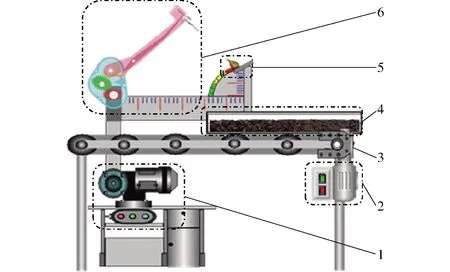
图8 大蒜直立移栽机构试验台示意图Fig.8 Experimental bench of vertically transplanting mechanism for garlic1.电机1 2.电机2 3.传送带 4.土槽 5.穴盘 6.移栽机构

4.2 试验材料

试验样本为由市场购买的金乡大蒜，通过人工分瓣、去踵，挑选蒜瓣肥大、底芽齐全、顶芽肥壮、色泽洁白、无伤口、无病斑的优质蒜瓣作为试验播种材料。经测量，单粒蒜瓣的基本物理特性参数为：高度均值为36.03 mm，宽度均值为20.62 mm，厚度均值为20.18 mm，质量均值为6.97 g。

4.3 试验设计与试验结果

参考GB/Z 26578—2011《大蒜生产技术规范》中的相关要求设计试验。首先进行单因素预备试验，确定移栽深度、机构转速、匹配速比作为试验因素，移栽后的大蒜倾斜角u作为直立度的评价指标。初步确定各试验因素的取值范围后，进行多因素组合试验。为寻求最佳参数组合并分析其交互影响，采用二次回归正交旋转组合试验设计方法安排试验，试验过程如图9所示，在完成大蒜移栽后，使角度仪的垂直方向与蒜瓣的鳞芽方向对齐共线，角度仪的读数即为大蒜的倾斜角。

试验因素编码如表6所示，试验方案设计与结果如表7所示，表中A、B、C分别为移栽深度h、机构转速n、匹配速比λ的编码值。

表6 试验因素编码Tab.6 Coding of experimental factors

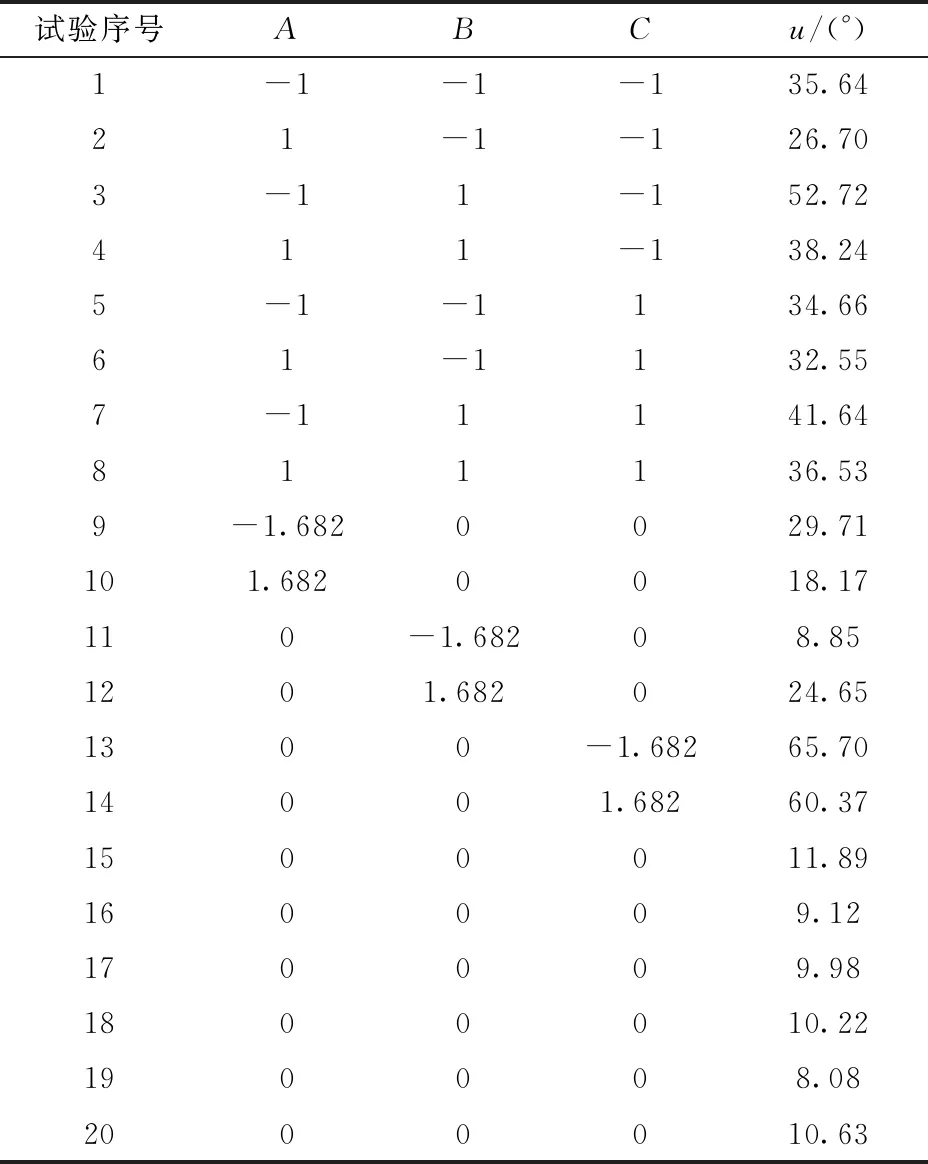
表7 试验方案与结果Tab.7 Experimental design and results

图10 试验模型响应曲面图Fig.10 Response surface maps of experiment

4.4 结果分析

采用Design-Expert软件对试验数据进行处理，得到各试验因素对倾斜角u影响的回归方程

u=9.35-3.66A+4.84B-1.24C- 1.07AB+2.03AC-2.21BC+ 5.20A2+2.66B2+19.02C2

(6)

通过对二次响应曲面模型的方差分析可知(方差分析表略)，模型F值为407.15，p<0.000 1，说明模型显著。模型中A、B、C、AB、AC、BC、A2、B2、C2各项p值均小于0.05，故均为显著项。失拟项F值为0.93，p=0.532 5，说明失拟项不显著。回归方程的决定系数R2=0.99，说明回归方程的预测值与实际值拟合良好。

根据所得回归方程，分别将其中一个因素固定在0水平，绘制出AB、AC、BC对倾斜角影响的响应曲面图，如图10所示。

由图10a可知，在匹配速比λ为100%的条件下，机构转速n和移栽深度h变化时，对倾斜角u的影响均不大。倾斜角u的最小值在移栽深度h约为15 mm时取得，其原因是当移栽深度h较小时，土壤对大蒜的粘结力不够，易受外界因素干扰，而当移栽深度h较大时，末端操作器与土壤之间的作用力变大，蒜瓣在入土时的阻力增大，从而引起倾斜角u变大。当移栽深度h一定时，随着机构转速n的升高，倾斜角u呈现不断增大的趋势，这是因为随着机构转速n的提高，机构的振动不断增加，导致移栽可靠性降低。值得注意的是，当机构转速n较高时，移栽深度h如果过浅，对倾斜角u的影响较大。因此，如果在实际生产中需要提高机构转速n，应当适当增加移栽深度h，以提高移栽的可靠性。

由图10b可知，在机构转速n为40 r/min的条件下，匹配速比λ和移栽深度h的变化对倾斜角u的交互影响作用较大。虽然随着移栽深度h的变化，倾斜角u整体变化较小，但当移栽深度h较小时，匹配速比λ的变化对倾斜角u的影响较为剧烈，因此移栽深度h宜取较大值。考虑到匹配速比λ的变化对倾斜角u影响的剧烈程度，其取值应尽可能在100%附近，若超出较大范围时，将无法获得满意的倾斜角。其原因是，当匹配速比λ变化时，末端操作器与土壤之间所形成的轨迹的直立程度降低，移栽时将形成较大的穴口。尤其是移栽深度h过浅，且匹配速比λ偏差较大的情况应当避免。

由图10c可知，在移栽深度h为15 mm的条件下，匹配速比λ和机构转速n的变化对倾斜角u的交互影响作用较大。随着机构转速n的降低，倾斜角u不断减小，移栽质量不断提高。由前述分析可知，匹配速比λ的变化对移栽结果影响较大，当偏离100%较大时，即使进一步降低机构转速n，对倾斜角u的提升效果也极为有限。在实际作业生产中，较低的机构转速n将降低移栽效率，因此，宜采取措施尽可能保证匹配速比λ的稳定，从而提升移栽作业质量。

根据上述分析结果，以倾斜角作为响应变量，以移栽深度、机构转速、匹配速比作为影响因素，根据优化目标建立相应的数学模型。当以倾斜角最小为优化目标时，建立的优化模型为

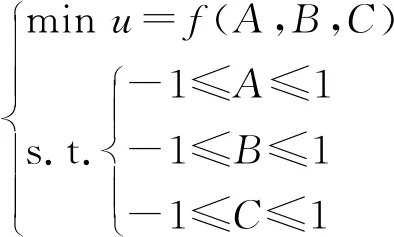
(7)

当将倾斜角限制在一定范围内时，则建立的优化模型为

(8)

式中umax——按农艺要求确定的倾斜角最大允许值，(°)

应用Design-Expert软件对式(7)的优化模型进行求解，得到优化参数组合方案：A、B、C取值为0.266、-0.821、-0.029，对应的实际值为h=17 mm,n=29.6 r/min,λ=100%，此时倾斜角的期望值为=7.37°。根据所得最佳参数组合方案进行验证性试验，在最佳参数组合方案条件下获得的倾斜角平均值为得到的响应值接近理论值，表明移栽机构工作可靠，回归方程与实际情况符合较好。试验中产生误差的原因有：每次移栽时的土壤性质无法重复；移栽机构在移栽过程中会产生振动；试验时蒜瓣个体的物理特性各不相同。

对式(8)的优化模型进行求解，假定umax=15°，从得到的多组优化参数组合方案中选取一组机构转速相对较高且匹配速比接近0水平的方案：A=0.629,B=0.601,C=-0.198，对应的实际值为h=19 mm,n=47.1 r/min,λ=98%，此时倾斜角的期望值为=14.17°。验证结果显示，在该参数组合方案条件下获得的倾斜角平均值为该结果亦在工程允许的范围内，满足大蒜栽植的直立度要求。

5 结论

(1)根据大蒜鳞芽直立朝上栽植的农艺需求，对大蒜移栽所需实现的轨迹与姿态进行了分析，设计了一种二阶非圆齿轮行星轮系大蒜直立移栽机构。

(2)采用D-H方法建立了移栽机构的数学模型，在Matlab平台下开发了机构的GUI优化设计软件，通过参数导引启发式优化算法实现了多参数、多目标条件下的复杂机构轨迹优化，获得了机构的非劣解参数。

(3)以获得的优化参数作为驱动，将自上而下的关联设计方法引入移栽机构设计过程中，并进行了虚拟样机验证，优化了设计流程，保证了设计数据的一致性。

(4)试验结果表明，当移栽深度为17 mm、机构转速为29.6 r/min、匹配速比为100%时，获得的蒜瓣倾斜角平均值为8.54°，当提高机构转速时，验证了所得结果亦处于农艺要求的范围内。