物体重建中的定位及渲染问题研究

杜丽美,张剑妹

（长治学院计算机系，山西长治 046011）

当今信息技术迅猛发展，随之产生的电子产品越来越多，这就导致了人们在工作和日常生活中对虚拟事物的接触也越来越频繁。比如在工作和学习中可能要借助虚拟场景来解决难题，生活中要借助虚拟设备来实现各种智能控制，娱乐方面更是离不开虚拟世界。为了更好地营造虚拟场景氛围需要将现实生活中的各类物体以虚拟物体的状态展示在各种屏幕上，以供人类使用。

1 研究的主要问题

现实生活中的物体之所以真实是因为大多是三维的，人类用双眼观察这些物体会有远处的物体小，近处的物体大的特点，再加上自然光的照射，雾的存在等使得一个普通的物体出现了各种状态。要将真实物体变为虚拟物体，首先要解决的是虚拟物体在窗口上的定位和投影问题，其次是各种特殊效果的设置，比如光照、材质、纹理等，最后还要解决人与虚拟物体之间的交互问题。本文就从这些方面来研究对于现实世界中的三维物体如何正确而有效地转换为虚拟物体的过程。

2 窗口建模

一个物体要想展示在计算机屏幕上，首先要确定窗口的位置和大小、视口的位置和大小、视点的位置、投影的方式等问题[1-2]。

2.1 定位

计算机屏幕所对的坐标系为世界坐标系，其X、Y和Z轴的方向如图1所示，即垂直于屏幕向外的方向为Z轴正向。确定了坐标系后，就要确定屏幕窗口的位置和大小，可以借助函数（1）（2）来完成，其中（1）中的x0和y0表示屏幕窗口距离计算机屏幕左上角的位置坐标，（2）中的width0和height0表示屏幕窗口自身的大小；接着确定视口的位置和大小，视口可形象地理解为显示物体的窗口，视口与屏幕窗口的关系为：屏幕窗口中包含视口，视口仅仅是屏幕窗口的一部分，大多数情况视口与屏幕窗口大小和位置完全一样即“重叠”，视口设置函数为（3），其中x 和y 表示视口距离屏幕窗口左下角的位置坐标，width 和height 表示视口自身的大小。计算机屏幕、屏幕窗口、视口之间的关系见图2所示。

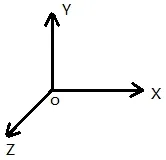
图1 世界坐标系

视点即对应着真实世界中人眼睛的位置坐标，眼睛位置选取的不同可以看到物体的面就不同，视点设置函数为（4），其中x1、y1和z1为人眼在世界坐标下的位置，x2、y2和z2为物体在世界坐标下的位置，x3、y3和z3为人眼看物体的方向（其实就是方向坐标）。

图2 屏幕、窗口、视口之间的关系

2.2 投影

投影是物体建模最关键的一步，分为正射投影和透视投影。正射投影的特点是不管物体离视点有多远，物体的大小都是不变的。透视投影的特点是离视点近的物体大，离视点远的物体小，透视投影符合我们日常生活中观察某个物体的特点，因此透视投影方式可以呈现出一种立体的效果，更接近真实场景。一般我们在三维建模中都使用透视投影的方式。两种投影方式对应的投影函数为（5）和（6），其中（5）中的参数如图3 所示，（6）中的参数x表示视点与裁剪面上端与下端形成的角度，y表示裁剪面的宽高比即width/height，z和h分别表示近裁剪面和远裁剪面沿Z 轴距视点的距离如图4 所示。不管是哪种投影方式，在调用投影函数之前都必须加上glLoadIdentity()和glMatrixMode()函数，前者表示还原当前矩阵为单位矩阵（也就是进行复位操作），后者表示投影模式（参数一般为GL_PROJECTION）。

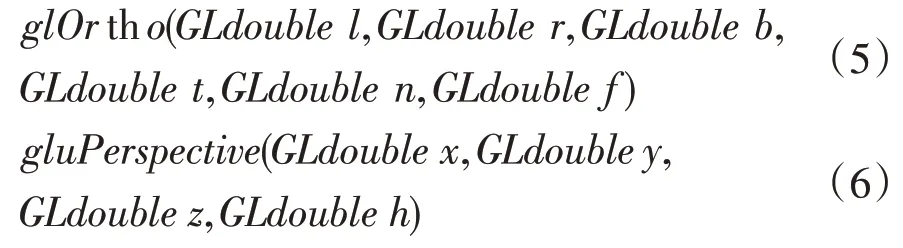
图3 正射投影视景体

图4 透视投影视景体

2.3 堆栈操作

堆栈操作经常用在模型的平移、旋转和缩放等变换中，堆栈操作[3]函数为式（7）和（8）所示。对模型进行各种变换其实就是使用各种变换矩阵M1,M2,…,与当前模型所在矩阵S进行相乘的操作，式（7）是将各种变换对应的矩阵M1,M2,…,压入栈中，目的是使变换矩阵与物体所在矩阵S做运算，运算的结果S’即为模型经过变换之后最终的位置；式（8）是将变换后的最终矩阵S’抛出，留下最初模型对应的矩阵S。

为了更加清晰地了解堆栈操作在图形变换中的重要作用，以图5 为例来进行具体的说明，图5中的五幅图展示了一个长方形在进行旋转的过程中，使用堆栈和不使用堆栈的最终效果，其中图5（a）为确定了窗口、视口、视点以及投影方式后，在屏幕中心位置画出的初始长方形，现对初始长方形进行旋转变换，每次旋转角度为5 度；图5（b）为使用了堆栈操作后，对长方形进行的第一次旋转，图5（d）为不使用堆栈操作对长方形进行的第一次旋转，由于是第一次旋转，所以两幅图的结果是一样的。图5（c）和图5（e）分别是使用和不使用堆栈操作对初始长方形进行的五次旋转后的结果，比较两次结果，假设变量i=0 为旋转度数，旋转一次相当于i+=5（这里的5 表示5 度），图5（c）由于使用了堆栈操作，在每一次旋转后都会将旋转变换后的矩阵抛出，只剩下初始长方形所在的初始矩阵，因而在进行第五次旋转时，i的值已经加到了25 度，25度对应的旋转矩阵和初始长方形所在的矩阵相乘，因此在经过了第五次旋转后最终的结果和图5（a）比较仅仅旋转了25度；图5（e）没有使用堆栈操作，可以理解为：第一次旋转i的值为5表示模型转动5度，第二次旋转i的值变为10表示在第一次旋转的基础上再旋转10 度，其实模型较图5（a）已经旋转了15度，…，第五次旋转时i的值为25是在第四次旋转的基础上进行的，因此第五次旋转后模型较图5（a）旋转了75度。

图5 使用堆栈和不使用堆栈对模型进行旋转效果对比

根据以上分析，当我们对模型进行平移、旋转、缩放等变换时，使用堆栈操作会更加接近真实情况，为此一般情况下都需要在程序的设计中加入堆栈操作函数。

3 特殊效果设置

为了渲染出更加真实的场景，需要对模型进行光照、雾化等的设置，设置不同颜色的光照可以使物体表面呈现出不同的颜色效果，使用雾化函数可以修饰周围的环境，更加逼近真实场景[4]。另外，为了达到人机交互的目的，可以借助键盘控制函数，来控制屏幕上模型的各种运动[5-6]。这些特殊效果可以使用式（9）～（12）来完成。

4 实验结果

通过以上分析，这里分别对两种物体进行了仿真模拟，当将窗口和视口大小均设置为（200，200），视点位置为（0，0，10），投影方式采用透视投影方式时图6（a）和图7（a）为对“茶壶”和“甜甜圈”两个物体的模拟效果，从结果中看到物体都是居中显示的。图6（b）和图6（c）为借助键盘控制函数对茶壶进行不同方向的旋转效果。图7（b）和图7（c）为在透视投影下，对物体在Z 轴负方向作平移后的效果，从结果中可以看到物体变的越来越小，而且实验中加入了雾化效果，当物体沿着Z轴负方向移动时会有雾的阻挡而颜色越来越不清晰。在图6 和图7 的仿真过程中，由于涉及到物体的移动问题，因此均使用了堆栈操作函数。

图6 茶壶模型的定位及渲染效果

图7 甜甜圈模型的定位及渲染效果

5 总结与展望

详细介绍了物体进行仿真建模过程中的定位问题、投影问题以及堆栈操作问题，这些问题要在物体建模初期确定下来，并且其解决的好坏决定了物体后期的仿真效果。除了这些问题以外，为了能够重建出非常逼真的模型，还需要对物体进行光照、材质、纹理[7]、雾化等的设置，这些只在文中简要地提到，还有待进一步研究。