基于QGA和随机共振的轴承微弱故障信号检测方法

葛江华 王岩 王亚萍 孙永国 许迪

摘 要：针对滚动轴承早期故障阶段振动信号微弱，信噪比低，提出量子遗传算法（quantum genetic algorithm，简称QGA）与随机共振相结合的微弱信号检测方法，提高信号信噪比并识别故障位置。首先，对大参数信号变尺度处理，并根据输入信号对噪声强度进行估计实现参数初始化;其次，以输出信噪比作为目标函数，通过QGA对系统的双参数进行自适应寻优;最后，通过系统的随机共振实现微弱信号信噪比的提高。仿真及实验结果表明，该方法充分考虑了系统参数之间的相互作用，能够有效提高信号信噪比，实现了早期故障阶段的微弱信号检测。

关键词：早期故障诊断;微弱信号检测;量子遗传算法;随机共振

DOI：10.15938/j.jhust.2020.03.015

中图分类号： TH165+.3;TN911.7

文献标志码： A

文章编号： 1007-2683（2020）03-0094-08

Abstract：Aiming at the problems that the vibration signal is weak and the SNR is low in its early failure stage of rolling bearing， a weak signal detection method combining Quantum Genetic Algorithm （QGA） and Stochastic Resonance is proposed， which improves SNR and identifies fault location. Firstly， the large parameter signal is scale transformed and the noise intensity is estimated according to the input signal to realize the initialization of the parameters. Secondly， the output SNR is selected as the objective function， and the two parameter are dealt with adaptive optimization through the QGA; Finally， the SNR of weak signal is improved by stochastic resonance system. Simulation and experimental results show that the method fully considers the interaction between system parameters， and can effectively improve SNR， and achieve early detection of weak signal in failure stage.

Keywords：early fault diagnosis; weak signal detection; quantum genetic algorithm; stochastic resonance

0 引 言

微弱信号检测目前在各领域内得到了广泛研究与发展。微弱信号检测是将深埋在环境噪声中的微弱信号提取出来，或提高微弱信号的信噪比。目前应用广泛的有时域平均法、相关检测法、混沌理论法和窄带滤波法等[1-3]。

随着非线性动力学與各交叉学科的快速发展，随机共振[4-7]方法在微弱信号检测领域得到了广泛的关注。随机共振方法与上述方法的信号处理机制不同，它将滤除噪声转变为利用噪声增强微弱信号，即将噪声信号中的能量转移到有用信号中。冷永刚等[8]提出一阶线性系统调参广义随机共振的特征提取方法，通过调整一阶线性系统参量，获得信噪比在取极大值情况下的广义随机共振;Tan等[9]通过引入二次采样解决大参数对随机共振效果的影响;Mba等[10]将随机共振用于健康的齿轮箱并探讨诸如残余信号和滤波信号计算的方法，以帮助遏制假警报，同时提高整体随机共振结果;Krauss等[11]提出了传感器的输出可以确定激励随机共振产生的噪声强度。

采用传统随机共振对加噪信号进行处理，在不调节系统参数的情况下，也就是默认a=1、b=1的情况下，随机共振现象并没有发生。前文已说明随机共振的产生取决于输入信号，噪声和非线性系统的协同作用，目前输入信号已知，噪声的强度也仅是高于输入信号，而不是强度过大完全掩盖信号，说明是系统内的参数存在问题。

系统的信噪比由噪声强度和势垒协同作用，在噪声一定的时候，系统的信噪比与势垒的关系如图6所示。可以看出系统的输出信噪比是在随着势垒的变化而变化。通过调节系统参数使势垒发生变化，当信号的势垒逐渐增大时，信号的信噪比先增加后减小，说明只有当势垒、信号、噪声达到一个最佳关系时，才能保证随机共振的信噪比最高。

为了进一步研究最佳的系统参数，对加噪信号采用双变量自适应随机共振。如图7所示为量子遗传算法对随机共振系统参数的寻优图。这里以信噪比作为适应度函数，自适应调节系统参数a和b，由图可见，顶部区域为满足最大信噪比的最优近似解。

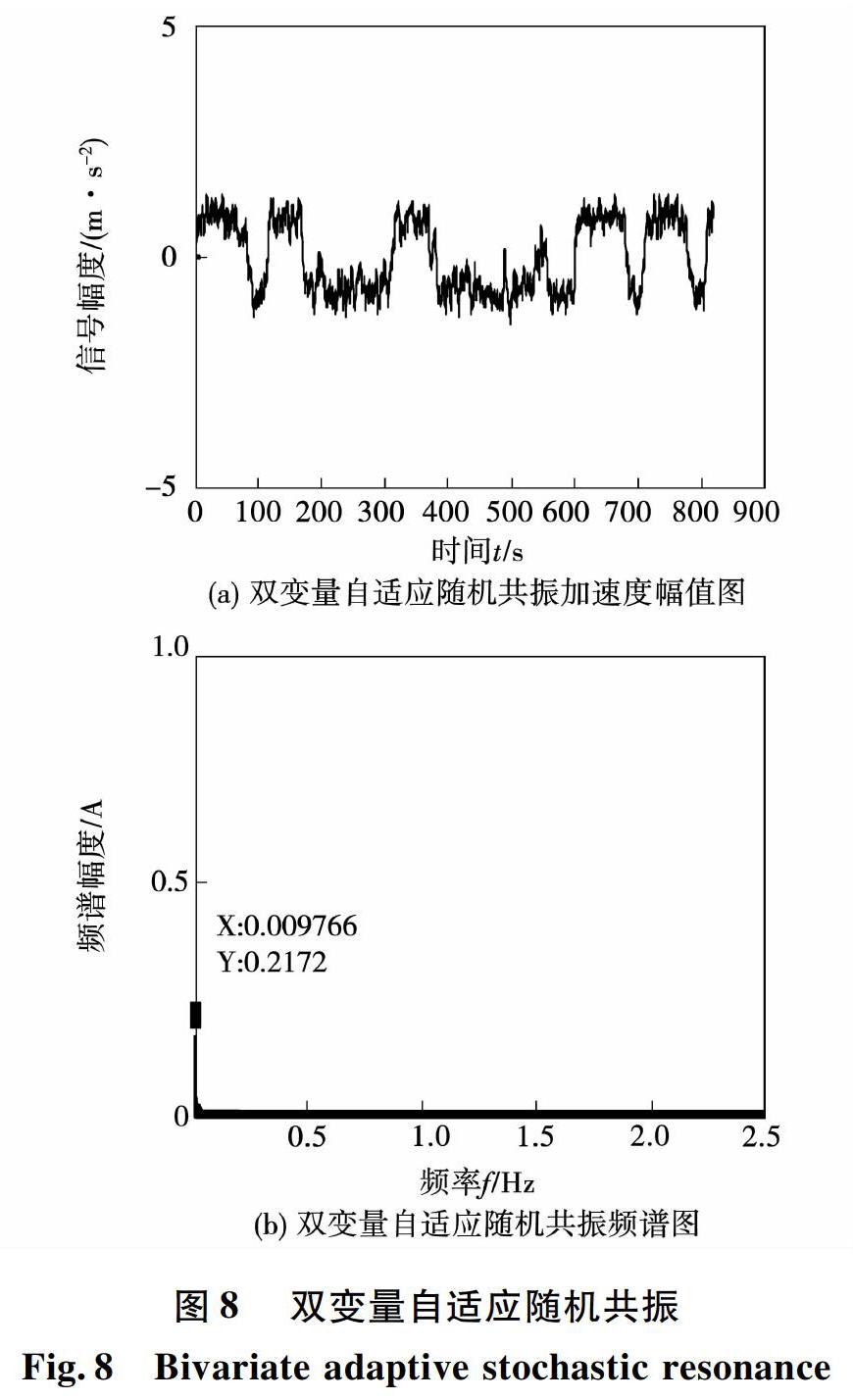
通过计算得到的系统参数值，a=0.27588，b=0.40685输入到系统中产生随机共振如图8所示。可以看出相对于图，波形已经呈现一定周期性，从频域可以发现在0.01Hz（图中为0.009766Hz，在可接受的误差范围之内）处有明显的频率，幅值为0.2172，相对于原信号的幅值0.002245得到了很大的提高。

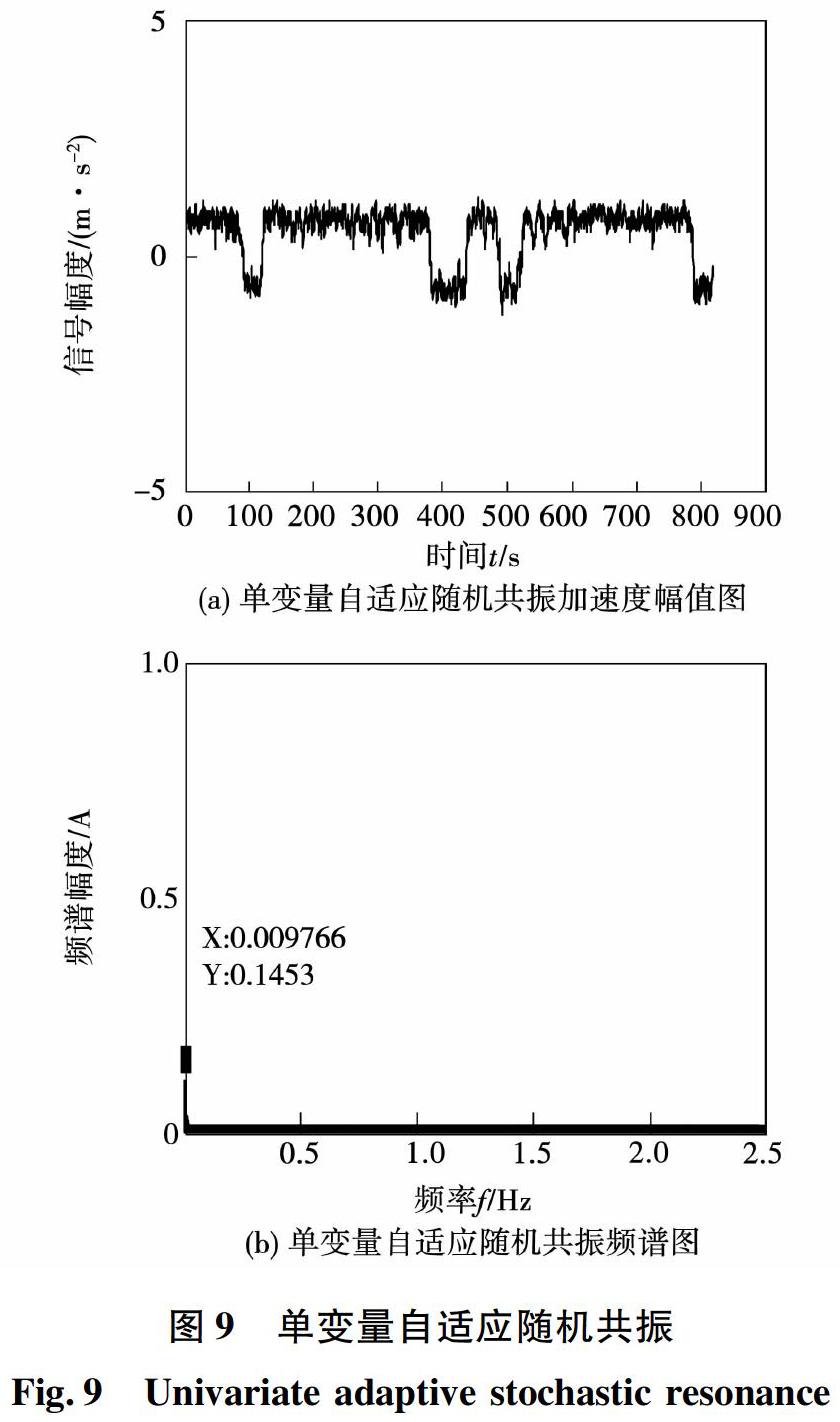
作为对比，这里也对单变量的优化进行了仿真，如图9所示。

当固定一个参数b=1，通过遗传算法可以得到a=0.7746，代入系统中产生随机共振，可以看到频率的幅值为0.1453，要小于双变量自适应随机共振的结果。

通过与传统随机共振、单变量自适应随机共振对比发现，本节的方法要优于前两种方法。对于微弱信号和复杂信号，频率通常深埋在噪声频率中不易识别，该方法可以最大程度提高频率幅值，更有利于故障的识别。

3.2 实验验证

本文将采用双列角接触球轴承故障模拟试验来验证本文提出的微弱信号检测、信号分解、降噪与特征提取方法的有效性。实验室搭建的滚动轴承振动测试试验台如图10所示。试验台主要组成有：SGM7J-04AFC6S伺服电机，额定输出400W，额定电流2.5A，额定转矩1.27N·m，额定转速3000r/min;YMC122A100加速度传感器，频率范围0.3-10KHz;POD-0.6kg磁粉制动器，电压24V，电流0.81A，额定转矩6N·m，最高转速1800r/min;GFC-40X66梅花联轴器;底座与轴承座、连接件与紧固件。

试验对象为3204ATN双列角接触球轴承，如图12所示，具体参数如表1所示。根据滚动轴承常见故障位置与故障类型，本文实验主要模拟内圈磨损故障。内圈磨损情况如图11所示，图中圈内的即为磨损位置。转速n=2400r/min，采样频率f=2560Hz，基本参数如表1所示，根据参数和式（11）得到内圈的故障频率约为fi=192.84Hz。

式中：Z为滚动体个数;f0为主轴的转频;d、D为滚动体直径和節圆直径;α为接触角。

原始信号的幅值图和频谱图如图12所示。外圈裂痕信号的噪声方差估计值σ2=0.1034，D=0.0064625，A=0.04294，此时信号幅值大于信号的噪声强度，因此添加噪声强度D=0.2的白噪声，

由于实际信号不满足随机共振小参数要求，所以先经过变尺度缩小采样频率，尺度压缩比R=512，对信号尺度变换之后，采样频率fs=f/R=5Hz。

根据量子遗传算法寻优得到a=1.64278，b=17.4642，随机共振得到的频谱图如图13所示，经过尺度还原比例f=0.38627R=197.77Hz，接近内圈故障频率，可以看出转频和故障频率都有一定程度的增强。

作为对比，这里也对单变量的优化进行了仿真，如图14所示。

当固定一个参数a=1，通过遗传算法可以得到b=16.3541，代入系统中产生随机共振，可以看到故障频率处的幅值为0.1488，要小于双变量自适应随机共振的结果。

4 结 论

本文提出一种量子遗传算法与随机共振相结合的微弱信号检测方法，通过仿真与实验验证得到以下结论：

1）大参数信号经过变尺度处理并不影响故障频率;信号中的噪声强度要通过计算以确定是否需要添加额外白噪声。

2）量子遗传算法对于随机共振系统参数的优化效果要优于传统方法和单一参数优化。

3）通过仿真和实验数据的验证，本文方法可以对早期故障阶段的微弱信号进行检测，得到具体的故障频率，实现故障位置的识别。

参 考 文 献：

[1] 王亚萍， 许迪， 葛江华，等. 基于SPWVD时频图纹理特征的滚动轴承故障诊断[J]. 振动、测试与诊断， 2017， 37（1）：115.

WANG Yaping， XU Di， GE Jianghua， et al. Fault Diagnosis of Rolling Bearings Based on Texture Features of SPWVD Time-frequency Map [J]. Vibration， Test and Diagnosis， 2017， 37 （1）： 115.

[2] 郭丹枫，庞兵.振动信号处理的时频域方法[J].哈尔滨理工大学学报，2007（4）：15.

GUO Danfeng， PANG Bing.Time-frequency Domain Method of Vibration Signal Processing [J] .Journal of Harbin University of Science and Technology， 2007 （4）： 15.

[3] LIU Y， ZHANG J Z. Predicting Traffic Flow in Local Area Networks by the Largest Lyapunov Exponent [J]. Entropy，2016，18（1）：1.

[4] CHEN H， VARSHNEY P K， KAY S M， et al. Theory of the Stochastic Resonance Effect in Signal Detection： Part I-Fixed Detectors[J]. IEEE Transactions on Signal Processing， 2007， 55（7）：3172.

[5] CHEN H， VARSHNEY P K. Theory of the Stochastic Resonance Effect in Signal Detection-Part II： Variable Detectors[J]. IEEE Transactions on Signal Processing， 2008， 56（10）：5031.

[6] MONIFI F， ZHANG J， AHIN Kaya zdemir， et al. Optomechanically Induced Stochastic Resonance and Chaos Transfer Between Optical Fields[J]. Nature Photonics， 2016， 10（6）：399.

[7] LU S， HE Q， KONG F. Stochastic Resonance with Woods-Saxon Potential for Rolling Element Bearing Fault Diagnosis[J]. Mechanical Systems & Signal Processing， 2014， 45（2）：488.

[8] 冷永剛， 田祥友. 一阶线性系统随机共振在转子轴故障诊断中的应用研究[J]. 振动与冲击， 2014， 33（17）：1.

LENG Yonggang， TIAN Xiangyou. Application of First-order Linear System Stochastic Resonance in Rotor Shaft Fault Diagnosis [J]. Vibration and Shock， 2014， 33 （17）： 1.

[9] TAN J， CHEN X， WANG J， et al. Study of Frequency-shifted and Re-scaling Stochastic Resonance and Its Application to Fault Diagnosis[J]. Mechanical Systems & Signal Processing， 2009， 23（3）：811.

[10]MBA C U， MARCHESIELLO S， FASANA A， et al. On the Use of Stochastic Resonance for Fault Detection in Spur Gearboxes[J]. Diagnostyka， 2017， 18（3）：3.

[11]KRAUSS P， METZNER C， SCHILLING A， et al. Adaptive Stochastic Resonance for Unknown and Variable Input Signals[J]. Scientific Reports， 2017， 7（1）：2450.

[12]焦尚彬， 李鹏华， 张青，等. 采用知识的粒子群算法的多频微弱信号自适应随机共振检测方法[J]. 机械工程学报， 2014， 50（12）：1.

JIAO Shangbin， LI Penghua， ZHANG Qing， et al. Multi-frequency Weak Signal Aaptive Stochastic Resonance Detection Method Using Knowledge Particle Swarm Optimization [J]. Journal of Mechanical Engineering， 2014， 50 （12）： 1.

[13]崔偉成， 李伟， 孟凡磊，等. 基于果蝇优化算法的自适应随机共振轴承故障信号检测方法[J]. 振动与冲击， 2016， 35（10）：96.

CUI Weicheng， LI Wei， MENG Fanlei， et al. Adaptive Stochastic Resonance Bearing Fault Signal Detection Method Based on Fruit Fly Optimization Algorithm [J]. Vibration and Shock， 2016， 35 （10）： 96.

[14]DEY S， BHATTACHARYYA S， MAULIK U. Quantum Inspired Genetic Algorithm and Particle Swarm Optimization Using Chaotic Map Model Based Interference for Gray Level Image Thresholding[J]. Swarm & Evolutionary Computation， 2014， 15：38.

[15]XU K J， REN S， QIN H Q， et al. Rolling Bearing Fault Diagnosis Based on Quantum Genetic Algorithm and Spectral Kurtosis[J]. Zhendong Yu Chongji/journal of Vibration & Shock， 2015， 34（11）：105.

（编辑：温泽宇）