复合控制算法在光伏MPPT中的应用
王胜辉 李宜伦 郑洪 高山


摘 要:针对光伏阵列受到局部阴影遮挡或光照不均匀时输出呈现多峰值特性,传统单峰值MPPT算法难以追踪到最大功率点的问题,提出一种改进粒子群结合滑模层极值搜索的复合算法。首先在标准粒子群算法中引入改进模拟退火算法的概率判断准则;改进惯性权重变化规律;对其学习因子中加入扰动参数,其次利用滑模层极值搜索算法对粒子群算法所得的疑似最优值进行继续寻优,最后寻得最大功率点。仿真结果表明,复合控制算法能够在不同阴影条件下快速、准确的跟踪最大功率点,避免系统陷入局部最优值。
关键词:光伏发电;局部阴影;最大功率点跟踪;粒子群算法;滑模层函数; 参数调整
DOI:10.15938/j.jhust.2020.03.010
中图分类号: TM914.4
文献标志码: A
文章编号: 1007-2683(2020)03-0061-07
Abstract:Aiming at the problem that the output array exhibits multi-peak characteristics when the PV array is partially shaded or unevenly illuminated, the traditional single-peak MPPT algorithm is difficult to track the maximum power point. A hybrid algorithm is proposed to improve the particle swarm combined with the sliding mode search. Firstly, the probability judgment criterion of improved simulated annealing algorithm is introduced into the standard particle swarm optimization algorithm; the law of inertia weight change is improved; the disturbance parameter is added to the learning factor. Secondly, using the sliding mode extreme value search algorithm, the suspected optimal value obtained by the particle swarm optimization algorithm is continuously optimized, and finally the maximum power point is found. The simulation results show that the composite control algorithm can track the maximum power point quickly and accurately under different shadow conditions, and avoid the system falling into the local optimum value.
Keywords:photovoltaic power generation;local shadow; MPPT; particle swarm optimization; sliding layer function; parameter adjustment
0 引 言
局部陰影下光伏系统存在多峰值特性,控制光伏系统以此来保持其最大功率的输出是光伏发电系统提升效率的关键[1]。传统的控制方法如扰动观察法、电导增量法等[2-5]都能够快速实现单峰值的最大功率跟踪。但是实际生活中由于遮蔽影响,光伏电池会依据自身特性和阴影分布呈现多峰值的特性,传统的控制方法在解决多峰值问题时,往往会陷入局部最优解,使光伏系统整体的发电效率降低。因此,多峰值光伏最大功率跟踪问题的研究具有非常重要的现实意义[6]。
当前,针对局部阴影下光伏电池的特性和多峰值最大功率跟踪的控制算法,已经有了大量的研究。文[7-8]分别建立了不同局部阴影下光伏电池的数学模型,分析了光伏阵列在不同光照强度、遮挡模式、阴影分布和阵列格局下的输出特性。文[9]提出全局搜索和电导增量相结合的方法,通过阈值的合理选取能够快速准确的找到最大功率点;但是参数的选取需要大量的实验数据,存在误差。萤火虫算法[10]、粒子群算法(particle swarm optimization,PSO)[11]、遗传算法[12]等智能算法也广泛应用于光伏最大功率点跟踪,它们不易陷入局部最优值,提高了跟踪速度,但是参数选取复杂。文[13]提出了一种粒子群算法和变步长扰动观察法相结合的算法,该方法首先通过粒子群算法迅速定位近似最大功率点,变步长扰动观察法根据实际情况精确定位至最大功率点,但是该方法利用改进的Fibonacci数列作为变步长扰动观察法步长改变的依据,具有较大的误差。文[14]采用一种改进的滑模变结构控制方法进行最大功率点跟踪,在传统滑模变结构控制的滑模面选择基础上加入积分运算并且把指数趋近律与等效控制相结合,该方法减小了稳态误差,加快了跟踪速度。标准粒子群算法作为一种能够全局搜索的智能算法具有搜索能力快、易于实现的优点[15-16],但是也有易陷入局部最优值、搜索精度低的缺点;滑模层极值搜索算法具有稳定性高、鲁棒性强的特点。本文对PSO中的迭代准则、权重值和学习因子分别进行改进。算法首先使用改进粒子群算法进行全局寻优,在改进粒子群算法收敛后使用滑模层极值搜索算法进行局部寻优,得到全局最优值。最后通过Matlab/Simulink进行仿真验证,结果表明该方法具有应对光照强度发生变化的能力,效率高、动态性能好、跟踪迅速,极大提高了光伏系统的发电效率。
1 局部阴影下光伏阵列的输出特性
光伏阵列是将单一电池进行串并联的物理组合而成,如图1所示为3×3光伏阵列,其中每个光伏电池组件都并联一个并联二极管,其主要目的是为了防止热斑现象,但是这种做法就导致了光伏电池在局部阴影条件下出现了多峰值特性。
通过Matlab/Simulink搭建如图1所示的光伏阵列仿真模型组,光伏阵列在不同阴影下,其功率输出特性曲线如图2所示。
图2中无阴影情况为图1中三列光伏电池光照强度均为1000W/m2;阴影1情况为左侧支列均为1000W/m2,中间与右侧均为800W/m2;阴影2情况为左侧支列为1000W/m2,中间支列为800W/m2,右侧支列为600W/m2。从图中可以看出当电池有阴影遮蔽存在时,电池输出功率也发生了变化,产生多个峰值。为了保证电池输出功率最大,需要一个全局搜索的寻优方法以实现阴影下最大功率的跟踪。
2 最大功率跟踪控制算法
2.1 改进粒子群算法
粒子群算法的核心思想是:在多个种群中的N个随机解,通过不断的迭代去找到自身的最优解。其基本原理为[17-18]
式中:c1、c2为学习因子;r1、r2为随机数;ω为线性权重;不同的参数设置对于整个系统寻优时间、精度的影响较大。同时标准算法搜索中不具备突跳能力、惯性权重值变化单一、学习因子适应性差,使得算法寻优时容易陷入早熟。为了提高寻优过程中的精度、降低搜索时间,采用如下方法对标准粒子群算法进行改进:
1)粒子群算法中,惯性权重ω是一个最重要的参数,ω值的大小与算法整体搜索能力有关,增大ω值可以提高算法整体的搜索能力,减少ω值可以提高算法局部的搜索能力。标准粒子群算法采用线性递减的变化方式,其变化规律为
式中:ωmax和ωmin分别为ω的最大与最小值;k为当前迭代次数;kmax为最大迭代次数。如图3为典型线性惯性权重的ω随迭代次数的变化曲线,其中最大迭代次数为50次,ωmax=0.85,ωmin=0.6。
ω值的大小是算法本身是否陷入局部最优解[17]和快速准确搜索的关键。常规的改进权重的粒子群算法有:自适应权重法、随机权重法、线性递减权重法。在进行最大功率跟踪时,权重值规律变化明显,算法初始阶段需要增大ω值以此来提高全局搜索能力;算法最后阶段需要减少ω值来提高局部搜索能力,ω值呈现一个非线性递减趋势,所以常规的权重改进方法并不适合最大功率跟踪当中。对此提出了一种非线性动态的惯性权重法[18],其权重变化规律为
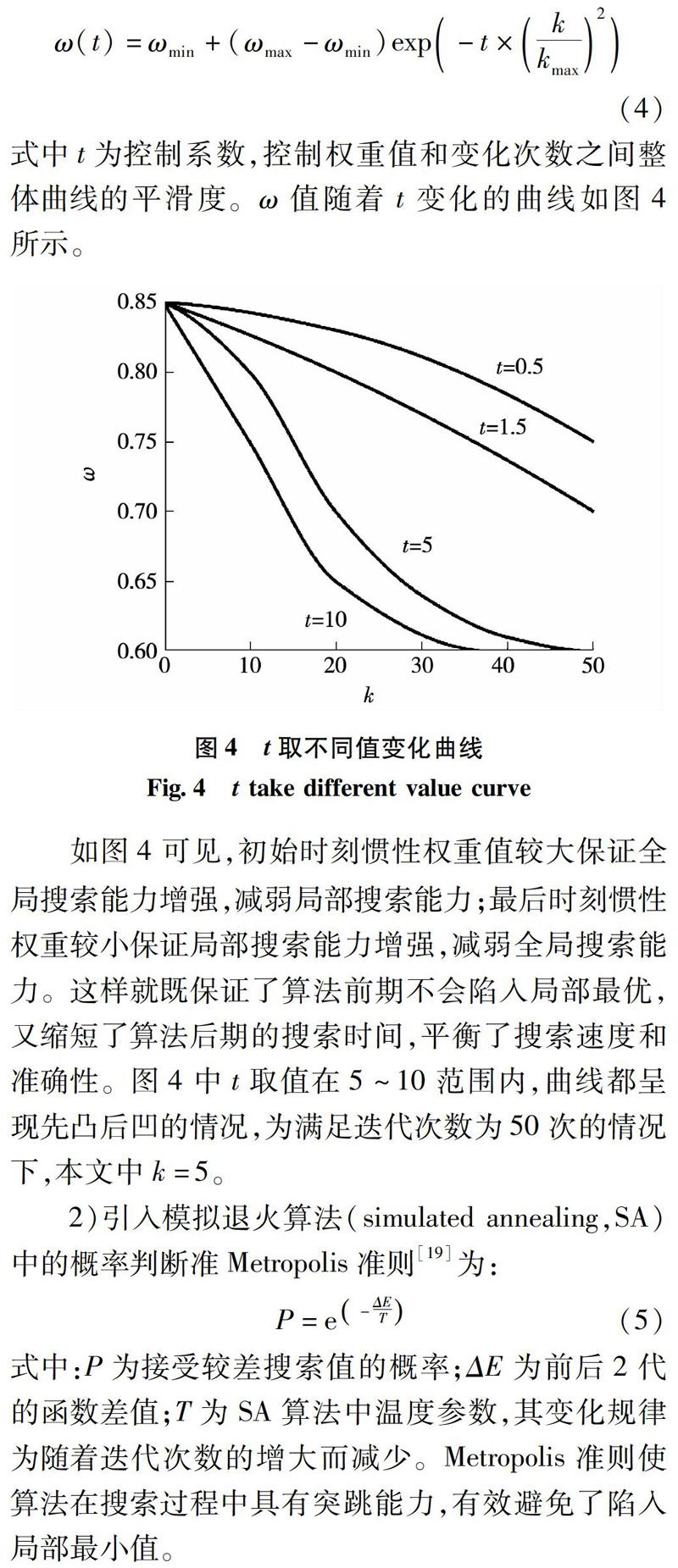
式中t为控制系数,控制权重值和变化次数之间整体曲线的平滑度。ω值随着t变化的曲线如图4所示。
如图4可见,初始时刻惯性权重值较大保证全局搜索能力增强,减弱局部搜索能力;最后时刻惯性权重较小保证局部搜索能力增強,减弱全局搜索能力。这样就既保证了算法前期不会陷入局部最优,又缩短了算法后期的搜索时间,平衡了搜索速度和准确性。图4中t取值在5~10范围内,曲线都呈现先凸后凹的情况,为满足迭代次数为50次的情况下,本文中k=5。
2)引入模拟退火算法(simulated annealing,SA)中的概率判断准Metropolis准则[19]为:
式中:P为接受较差搜索值的概率;ΔE为前后2代的函数差值;T为SA算法中温度参数,其变化规律为随着迭代次数的增大而减少。Metropolis准则使算法在搜索过程中具有突跳能力,有效避免了陷入局部最小值。
3)将SA算法中参数T的更新规则改为
其中:d为迭代次数;T0、Tend分别为T的初始值。
4)结合遗传算法中的变异思想,对学习因子c1、c2进行进一步的改进,通过加入扰动函数巩固了算法本身的局部搜索能力,扰动函数为
其中:rand为[0,1]间的随机数;η为扰动函数;a为非负的常数。
检验改进PSO算法收敛情况,验证改进算法是否易陷入局部最优值,其测试函数为
其测试结果为图5所示。
由图5可见,改进PSO算法在迭代次数为5时就已经寻得最优值,从循环中跳出,而常规PSO算法在9代时陷入局部最优值,并没有寻得最优解。改进PSO可以有效的防止系统陷入局部最优值。
2.2 滑模层极值搜索算法
滑模层极值搜索算法具有较快的收敛速度,其无需对系统进行详细的建模,只需要监视某些状态量就能够有效进行光伏发电系统最大功率跟踪控制[20]。结合改进PSO能够更加快速进行光伏最大功率点的跟踪。其输入量为上一层中输出的疑似最大功率值P′mpp,输出量为参考电压值Udcref,其具体控制结构如图6所示。Psref、u、δ为控制过程中的中间变量;sgn(δ)为符号参数;ρ、Z0、U0为正常数。
开关函数为控制的核心[20],为了避免开关频率过快引起噪音污染以及功率损失,引入滑模层函数代替原有的开关函数,使系统快速进入稳定,减少了相应的震荡。具体函数关系为:
在保证控制系统能够快速、稳定运行的同时,为了减少震荡,有效的提高控制的动态品质,因此对ρ、Z0、U0参数进行进一步的优化。可得:
对应的dP′mpp/dt∝U0∝P′mpp,即U0越大dP′mpp/dt越大,对应P′mpp变化越迅速,结合式(13)与式(14)可以近似得到:
从而可以得到dPsref/dt∝Z0,Psref变化的越快Z0越大。当系统P′mpp=Psref时,且P′mpp=Pmax时,意味着Psref诱导P′mpp追踪Pmax。因此P′mpp与Pmax之间的比值作为一个调整因子,能够使系统快速稳定在最大功率点,提高了动态稳定性。
定义参数调整系数γ,则动态调整参数调整系数为
其中ρ、Z0、U0参数满足式(13)。参数具体变化过程为:若γ<1,U0与Z0同时减少;若γ>1,U0与Z0同时增大;若γ=1,则参数保持不变。
2.3 复合控制算法在光伏MPPT中的应用
将改进粒子群算法和基于自适应滑模层极值搜索法结合,得到一个新的复合控制策略,其寻优过程为,第1阶段首先进行改进粒子群算法,初始化粒子位置、速度和适应度并存储最优值,其次更新粒子的位置和速度并更新权重值,将其比较选取最好的位置并更新最优值,最后满足条件输出最优的P′mpp;将改进粒子群算法后期收敛得到的P′mpp作为滑模层极值搜索算法的输入,第2阶段为滑模层极值搜索法,其中最大功率点理论计算值为:
即让P′mpp追踪到Pmax,确定最终的光伏最大功率点,若P′mpp已经追上Pmax,则应锁住相应的参数,避免叠加额外的扰动和过度时间。
3 仿真分析
本文采用Matlab/Simulink对系统进行仿真,光伏阵列模型为{2×2},其中每个光伏电池参数设置为:开路电压Uoc=23.36V,短路电流Isc=3A,峰值电压Um=18.47V,峰值电流Isc=2.8A。Boost升压电路参数设置为:滤波电容均为10-6F,电感0.5×10-6H,IGBT通断频率为2kHz。阴影设置如表1。
经过实验,扰动观察法、粒子群算法、混合控制算法在相同阴影状态下,其不同动态仿真结果如图7所示。
图7(a)可见,3种阴影状态下,扰动观察法功率均稳定在局部最大功率点而非全局最大功率点,且功率震荡严重;光照突变后震荡仍旧明显,具有稳态误差。因此扰动观察法无法有效的跟踪全局最大功率点跟踪。
图7(b)、(c)比较,3种阴影状态下,复合控制算法由于加入了滑模层极值搜索算法相对PSO收敛时间更短、震荡幅度更小、动态稳定性更高;虽然两种方法均能成功寻得最大功率点,但复合控制算法相对误差较低,光照发生突变瞬间,复合控制算法能够保持良好稳定性。其具体结果如表2所示。综上,复合控制算法相比PSO算法具有更好的精确性和快速性。
由仿真分析可知,复合控制算法可以快速、稳定的跟踪到最大功率点,不容易陷入局部最优值,具有良好的动态性能,寻优时间短,误差率更小,精度更高。
4 结 论
针对局部阴影下传统的扰动观察法容易失去作用和PSO算法容易陷入局部最优值的问题,本文提出了改进粒子群算法加滑模层极值搜索的复合控制算法,在粒子群算法中加入概率判断准则、改进权重值变化规律、学习因子增加了扰动参数,避免粒子群算法陷入局部最优值。同时对滑模层极值搜索算法中的参数进行了优化,提高了搜索时间和动态稳定性。最后通过仿真比较得到如下结论:①扰动观察法在复杂光照条件下,无法对最大功率点进行跟踪。②改进的复合控制算法在复杂光照情况下可以有效、稳定的追踪到最大功率點,并在速度跟精度上都有明显提升。
参 考 文 献:
[1] 吴志程,江智军,杨晓辉. 一种基于功率闭环控制的改进全局MPPT方法[J].电力系统保护与控制,2018,46(1):57.
WU Zhicheng, JIANG Zhijun, YANG Xiaohui. An Improved Global MPPT Method Based on Power Closed-loop Control[J]. Power System Protection and Control,2018,46(1):57.
[2] 倪双舞, 苏建徽, 周松林, 等. 部分遮挡条件下光伏阵列最大功率点跟踪方法[J]. 电机与控制学报, 2015,19(4):14.
NI Shuangwu, SU Jianwei, ZHOU Songlin, et al. Maximum Power Point Tracking Methods of Photovoltaic Array under Partially Shaded Condition[J]. Electric Machines and Control,2015,19(4):14.
[3] 刘云,应康,辛焕海,等.基于二次插值法的光伏发电系统控制策略[J].电力系统自动化,2012,36(21):29.
LIU Yun, YING Kang, XIN Huanhai, et al. A Control Strategy for Photovoltaic Generation System Based on Quadratic Interpolation Method[J]. Automation of Electric Power Systems,2012,36(21):31.
[4] 唐磊,曾成碧,苗虹,等.基于切线角的光伏变步长最大功率跟踪控制策略[J].电力系统自动化,2013,37(20):28.
TANG Lei, ZENG Chengbi, MIAO Hong, et al. A New Control Strategy for MPP Tracking in Photovoltaic System Based on Contingence Angle and Variable Stelrsize Searching Method[J]. Automation of Electric Power Systems,2013,37(20):28.
[5] 张开, 石季英, 林济铿, 等. 基于自适应滑模层极值搜索的光伏發电最大功率跟踪方法[J]. 电力系统自动化, 2015, 39(12):33.
ZHANG Kai, SHI Jiying, LIN Jikeng, et al. Maximum Power Point Tracking Method for Photovoltaic Systems Using Adaptive Extremum Seeking Control Based on Sliding Layer[J]. Automation of Electric Power Systems, 2015,39(12):33.
[6] 孙航,杜海江,季迎旭,等.光伏分布式 MPPT 机理分析与仿真研究[J].电力系统保护与控制, 2015, 43(2): 48.
SUN Hang, DU Haijiang, JI Yingxu, et al. Photovoltaic Distributed MPPT Mechanism Analysis and Simulation Study[J]. Power System Protection and Control, 2015, 43(2): 48.
[7] 刘邦银,段善旭,康勇,局部阴影条件下光伏模组特性的建模与分析[J].太阳能学报,2008,29(2):188.
LIU Bangyin, DUAN Shanxu, KANG Yong, Modeling and Analysis of Characteristics of pv Module Partial Shading[J]. Acta Energiae Solaris Sinica, 2008,29(2):188.
[8] 杨元培,杨 奕,王建山,等.光伏发电传输最大功率储能优化建模仿真[J].计算机仿真,2017,34(9):103.
YANG Yuanpei, YANG Yi, WANG Jianshan, et al. Model and Smulation of the Maximum Power Energy Storage Optimization in Photovoltaic Power Generation Transmission[J]. Computer Simulation, 2017,34(9):103.
[9] 李文强, 黎英, 张轩. 改进基于INC算法的光伏发电系统最大功率跟踪[J]. 电源技术, 2017(12):1737.
LI Wenqiang, LI Ying, ZHANG Xuan. Maximum Power Tracking of Photovoltaic Power Generation System Based on Improved INC Algorithm[J]. Chinese Journal of Power Sources, 2017(12):1737.
[10]DABRA V, PALIWAL K K, SHARMA P, et al. Optimization of Photovoltaic Power System:a Comparative Study[J]. Protection and Control of Modern Power Systems, 2017, 2(2): 29.
[11]LIU Y H, HUANG S C, HUANG J W, et al. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating Under Partially Shaded Conditions[J]. IEEE Transactions on Energy Conversion, 2012, 27(4):1027.
[12]劉建辉, 李博. 局部阴影下基于遗传蚁群算法对MPPT的研究[J]. 可再生能源, 2017, 35(1):13.
LIU Jianhui, LI Bo. Partial Shadow MPPT Based on Genetic Ant Colony Algorithm[J]. Renewable Energy Resources, 2017, 35(1):13.
[13]赵阳,张军朝,陶亚男,等. 基于粒子群优化变步长扰动观察MPPT算法[J].计算机仿真,2017,34(11):78.
ZHAO Yang, ZHANG Junchao, TAO Yanan, et al. MPPT Algorithm Based on Particle Swarm Optimizing Variable Step P&O[J]. Computer Simulation, 2017,34(11):78.
[14]颜景斌,王飞,王美静,等.改进滑模变结构控制光伏系统最大功率点跟踪[J].哈尔滨理工大学学报,2016,21(4):106.
YAN Jingbin, WANG Fei, WANG Yongliang, et al. Improved Sliding Mode Control for Maximum Power Point Tracking of Solar Photovoltaic Systems[J]. Journal of Harbin University of Science and Technology, 2016,21(4):106.
[15]ISHAQUE K, SALAM Z, SHAMSUDIN A, et al. A Direct Control Based Maximum Power Point Tracking Method for Photovoltaic System under Partial Shading Conditions using Particle Swarm Optimization Algorithm[J]. Applied Energy (S0306-2619), 2012, 99(11): 414.
[16]ROY C S,SAHA H. Maximum Power Point Tracking of Partially Shaded Solar Photovoltaic Arrays[J].Solar Energy Materials and Solar Cells,2010,94(9):1441.
[17]王秀云,赵宇,马万明,等.改进粒子群算法在无功优化中的应用[J].电测与仪表,2015,52(15) : 108.
WANG Xiuyun,ZHAO Yu, MA Wanming, et al. Application of Improved Particle Swarm Algorithm in Reactive Power Optimization[J]. Electrical Measurement&lnstrumentatinn, 2015,52(15) : 108.
[18]唐浩,楊国华,王鹏珍,等. 基于改进粒子群算法的风光蓄互补发电系统容量优化[J].电测与仪表,2017,54(16):50.
TANG Hao, YANG Guohua, WANG Pengzhen, et al. Capacity Optimization of Hybrid Wind-solar-battery Power System Based on Improved Particle Swarm Optimization[J] Electrical Measurement&lnstrumentatinn, 2017,54(16):50.
[19]程准,陆凯,钱煜,等.基于改进PSO算法的MAP图标定点选择新方法.[J].计算机应用研究,2018,36(10):3493.
CHEN Zhun, LU Kai, Qian Yu, et al. New Method of MAP Fixed-point Selection Based on Improved PSO Algorithm[J]. Application Research of Computers,2018,36(10):3493.
[20]PATEL H, AGARWAL V. Maximum Power Point Tracking Scheme for PV Systems Operating under Partially Shaded Conditions[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1689.
(编辑:温泽宇)

