多角度思考 妙手段处理——一道代数式最值的探究

陈永志

(黑龙江省大庆市大庆实验中学 163316)

在近年的模拟题、高考题、自主招生题或竞赛题中，经常会碰到求解多变元代数式的最值或取值范围问题，特别是双变元代数式的最值或取值范围问题．此类问题往往难度较大，思维方式多变，求解方法多样.

一、问题呈现

问题已知3=a2+c2-ac，则c+2a的最大值为____.

本题是一道双变元在已知条件下，相应的代数式的最值的求解问题．这类问题一直受备命题者的青睐．通过认真审视这道试卷，在不同视角下，得到了该题的不同解题思维与对应的精彩解法．

二、多解探究

思维角度1(判别式法1)设出所要求解的代数式c+2a=t，通过参数的转化代入已知的代数关系式建立关于某个字母的二次方程，结合二次方程的判别式法来确定参数t的取值范围，达到求解的目的．

解法1 设c+2a=t，则有c=t-2a.

由a2+c2-ac=3，可得a2+(t-2a)2-a(t-2a)=3，整理可得7a2-5ta+t2-3=0.

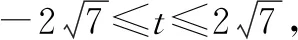
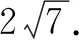
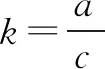
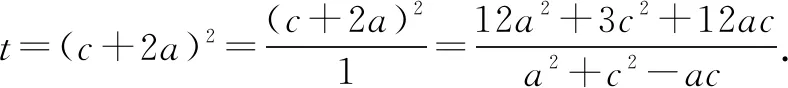
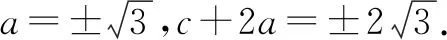
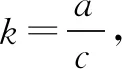
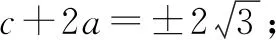
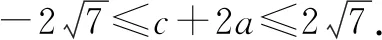
思维角度3 (基本不等式法)结合条件，利用配方公式以及基本不等式加以转化，进而确定代数式(c+2a)2的取值范围，通过求解二次不等式来确定相应代数式的最值问题．

解法3 由a2+c2-ac=3，则有3=a2+c2-ac=(c+2a)2-3a2-5ac，

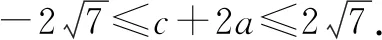
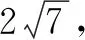
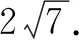
思维角度4 (三角换元法)根据已知关系式a2+c2-ac=3加以转化，利用三角换元思维引入参数，得到a、c的三角表达式，进而代入所求代数式c+2a，利用三角恒等变换，结合三角函数的图象与性质来确定其相应的最值问题．

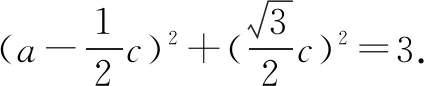
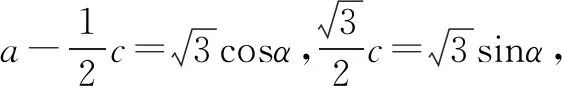
思维角度5 (柯西不等式法)根据已知关系式a2+c2-ac=3加以转化，结合所求代数式c+2a，配凑相应的系数，结合柯西不等式加以确定对应的关系式，再通过求解二次不等式来确定相应代数式的最值问题．

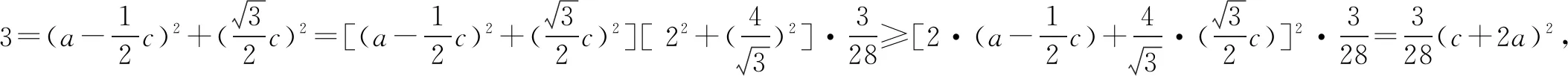
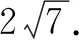
当我们解完一道题以后，要不断领悟反思，多角度切入进行深度挖掘，从而达到触类旁通、一题多解的效果．而通过典型模拟题实例的一题多解，可以使得我们的解题思路更加开阔，数学知识的掌握更加熟练，同时思维拓展，妙法顿生，提高解题速度，培养发散思维能力，有助于激发我们学习的主动性、积极性和趣味性，从而全面提高我们的知识水平和思维能力．