坐标法解决向量小题
叶文明 李 阳
(浙江省松阳二中 323406)
一般来说,代数问题较为抽象,若能通过构造将之合理转化为几何问题,利用“数形结合”这一重要思想方法,往往可增强问题的直观性,使解答事半功倍或独具匠心,数学家华罗庚曾经说过:“数离开形少直观,形离开数难入微.”利用数形结合的思想可构通代数、几何之间的关系,实现难题巧解.
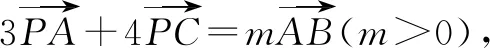
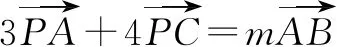

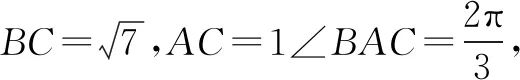
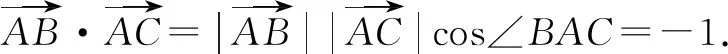
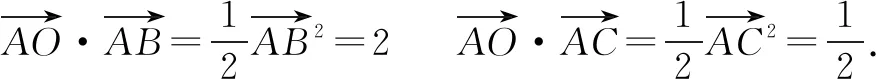

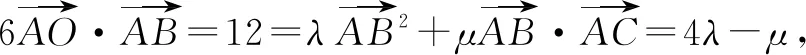
解方程组得λ=5,μ=8,∴λ+μ=13,
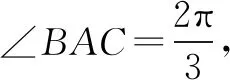
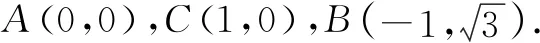

图2
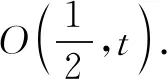

解得λ=5,μ=8,∴λ+μ=13.

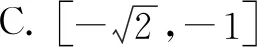
解析本题主要考查平面向量及其运算,基本不等式等知识,意在考查考生分析问题解决问题的能力.
设△ABC外接圆半径为1,由题意知m,n不能同时为正,
∴m+n<1①.
因为∠C=45°,O是△ABC的外心,所以∠AOB=90°.
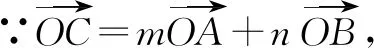
两边同时平方得1=m2+n2+2mncos∠AOB,
所以m2+n2=1②,
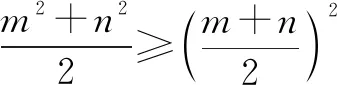
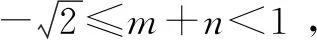

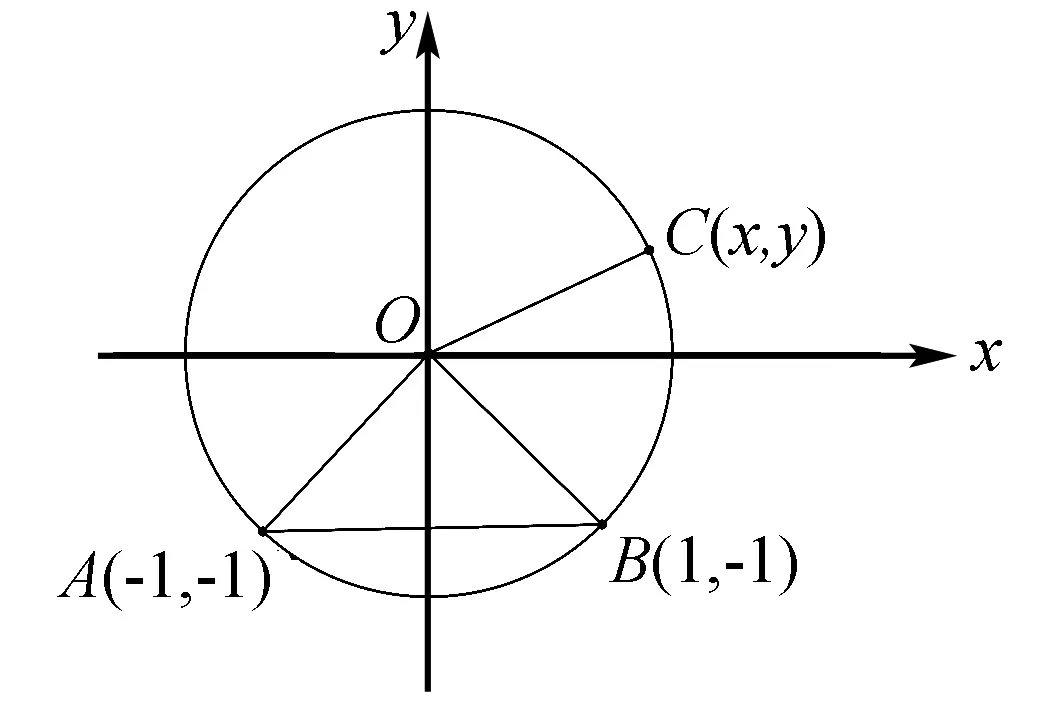
图3
代入x2+y2=2得m2+n2=1.
又y=-m-n>-1,∴m+n<1.
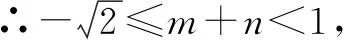
4.(2017绍兴高三质量调测)向量a,b满足|a|=4,b·(a-b)=0,若|λa-b|的最小值为2,则a·b为( ).
A.0 B.4 C.8 D.16
解析本题主要考查平面向量的模,数量积以及二次函数的最值等知识,以平面向量为载体,借助平面向量的模的最值求解,考查考生的坐标求解能力.
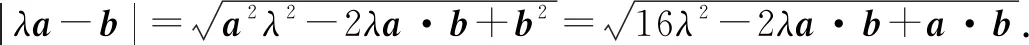
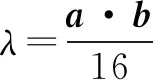
所以(a·b-8)2=0,故a·b=8,选C.
事实上,由已知可设a=(4,0),由b·(a-b)=0得b⊥(a-b).
所以b的终点在如图4以(2,0)为圆心的圆上.令b=(x,y),则x2-4x+y2=0,∴λa-b=(4λ-x,-y).
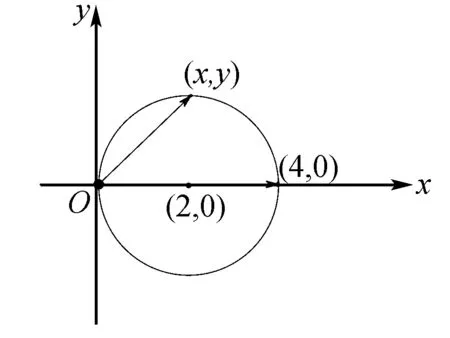
图4
|λa-b|
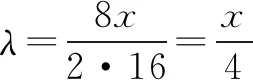
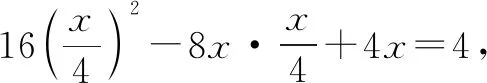
化为x2-4x+4=0,得x=2.
所以a·b=(4,0)·(2,y)=8,故选C.
5.(2017届浙江新高考研究联盟考卷)
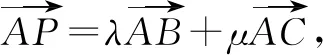


图5
直线BC:4x+3y-12=0,
直线BI:x+2y-3=0,
直线CI: 3x+y-4=0.
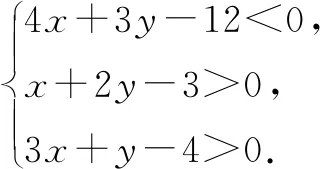
由(x,y)=λ(3,0)+μ(0,4) 得x=3λ,y=4μ.
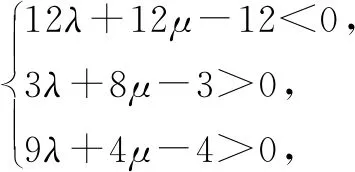
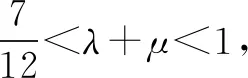
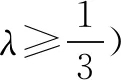
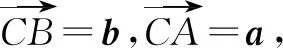
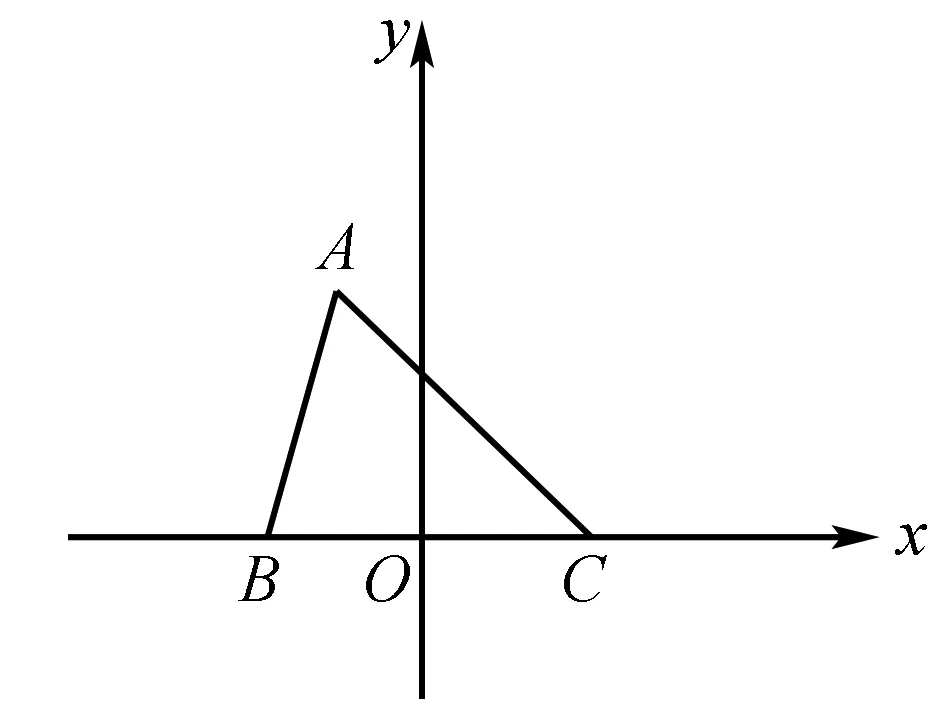
图6
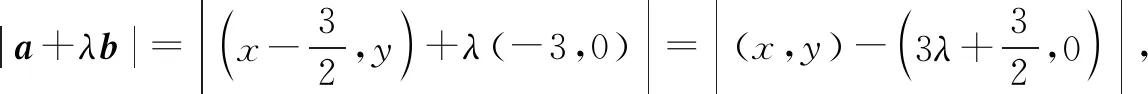
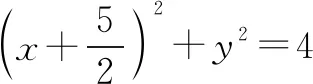

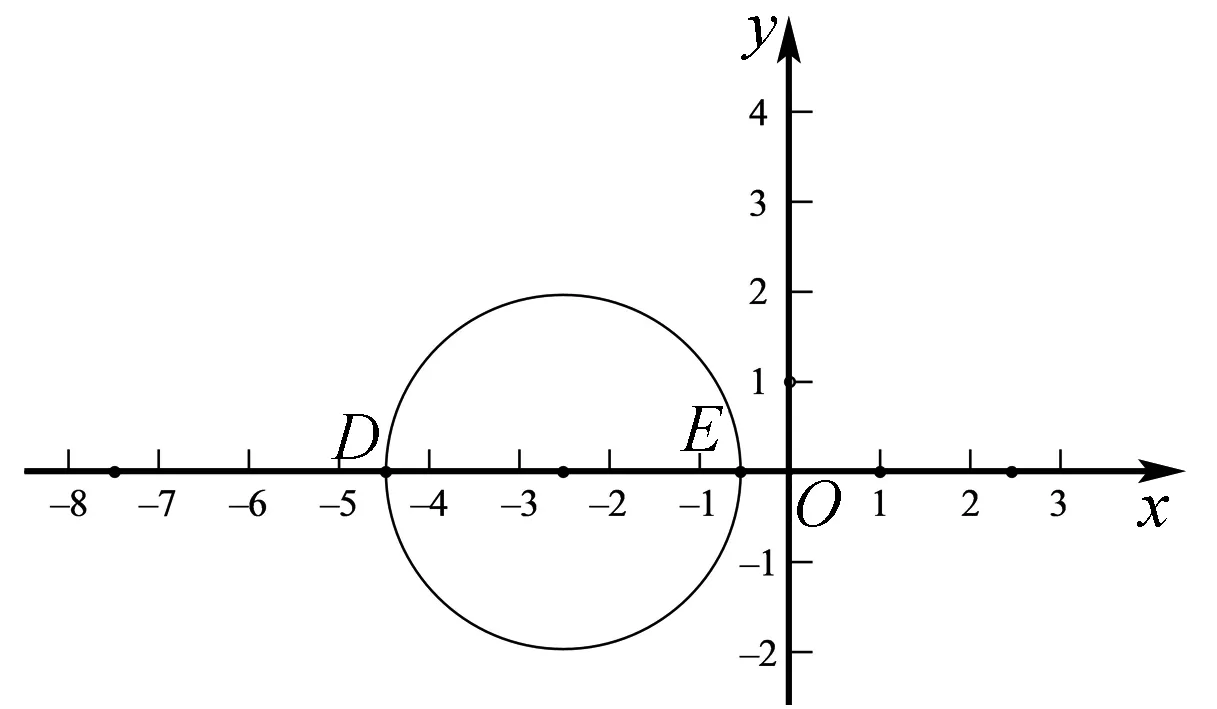
图7
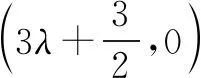
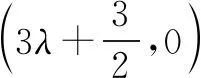

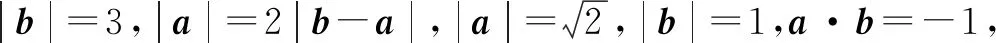
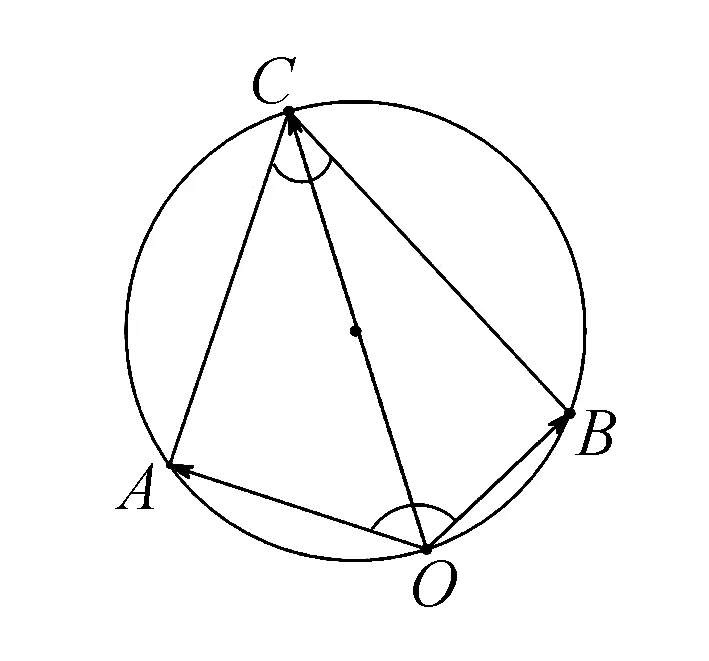
图8
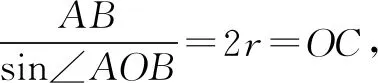
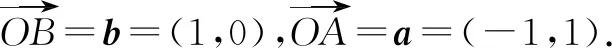
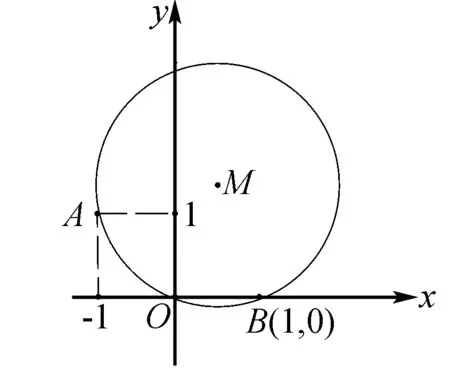
图9
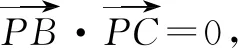
A -4 B.4 C.-2 D.0
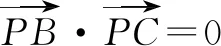
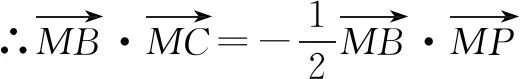
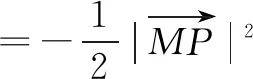
正确答案为C.
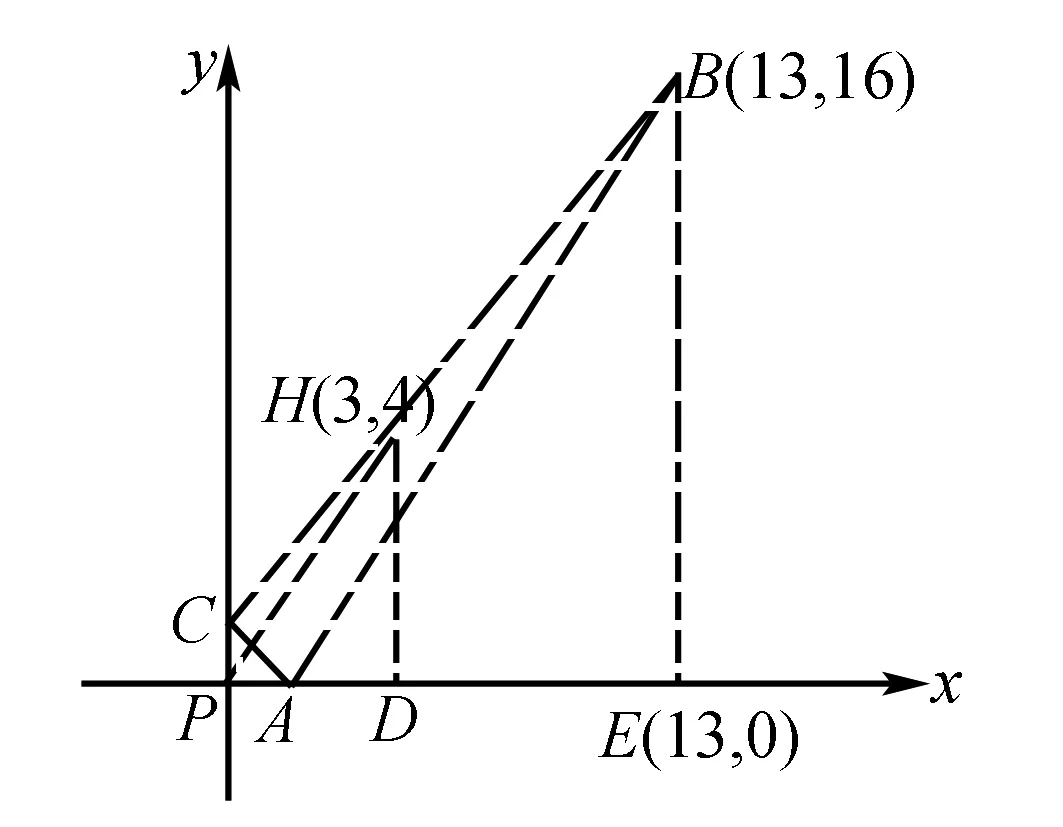
图1
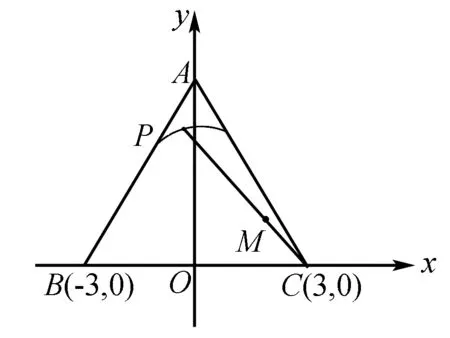
图10
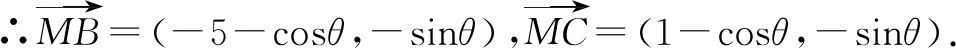

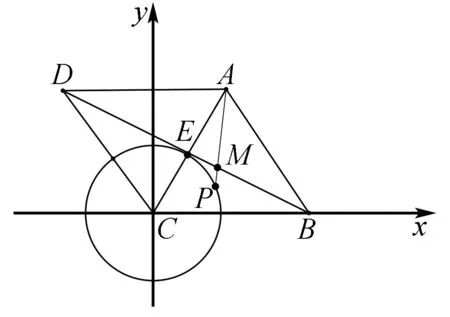
图11

