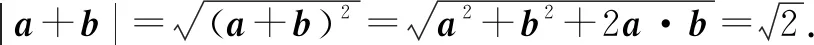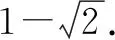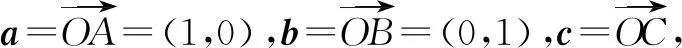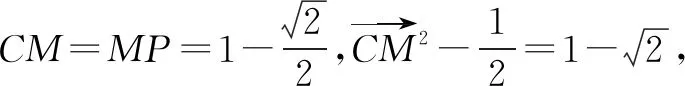理清解答困难 提升思维品质——以三道平面向量试题的一题多解为例

郑 良

(安徽省合肥市第四中学 230000)

解题时，若审题不够深入，只看到问题的表面现象，就会出现用运算代替思维(低效)甚至问题不可解(无效)的情况.这就提示我们要积累必要的知识、思想、方法(模型)，通过审题，将摄入的信息经过梳理、比对、分解、调整、加工、整合的过程，思维贯通后以合理的形式输出.

平面向量是高中数学的重要内容，也是高考的热点之一.平面向量兼顾“数”与“形”的两重性，形成了其独特的知识体系与思想方法体系.平面向量往往与三角、解析几何、函数、不等式等知识交汇，从而呈现出表示方法多、联系知识广、解题思路灵活等特征.学生在解题时常常会遭遇困惑：是从形的角度还是从数的角度入手较好？ 如何找到比较简捷的方法等等.本文通过对三道平面向量试题的一题多解，示范探寻解题的切入点，给出解法的合理性分析，比较解法的差异，期待能对大家的解题分析能力的提高及理性思维的提升有所帮助.为节省篇幅，本文以解答和点评的形式给出.

例1 已知平面向量a=(1,2)，b=(4,2)，c=ma+b(m∈R)，且c与a的夹角等于c与b的夹角，则m=____.

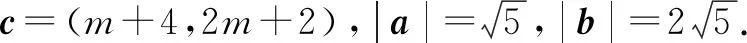
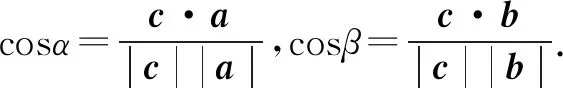
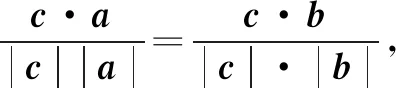
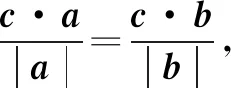
解得m=2.

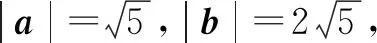
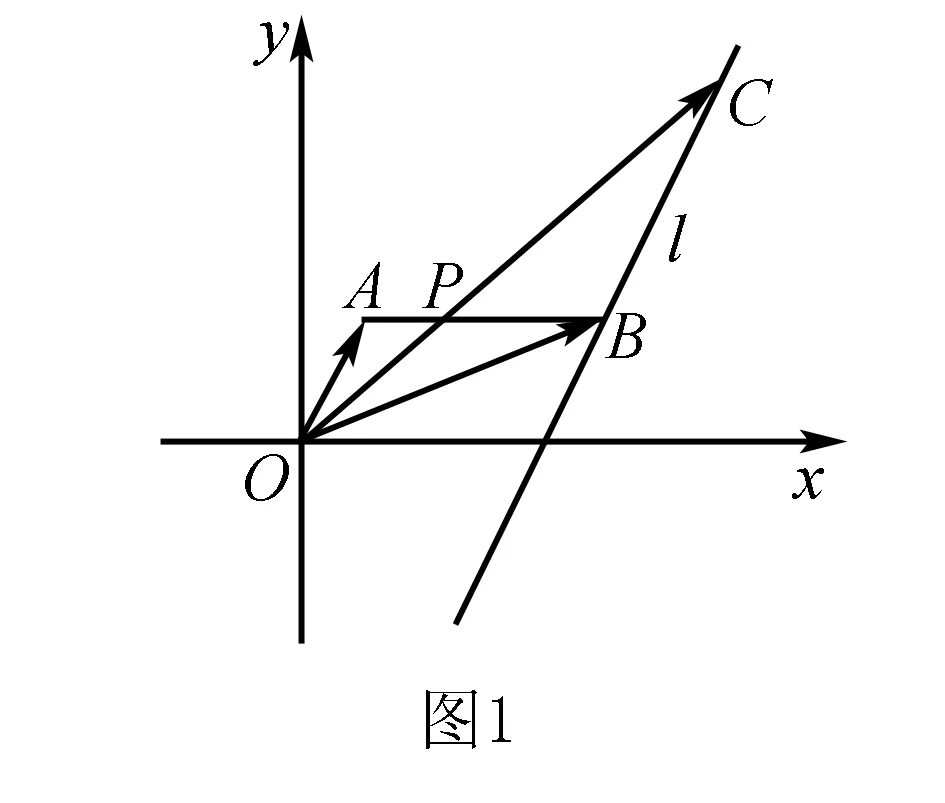
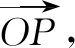
例2若向量a=(k,3)，b=(1,4)，c=(2,1)，已知2a-3b与c的夹角为钝角，则k的取值范围是____.

解法1 因为2a-3b与c的夹角为钝角，又2a-3b=(2k-3,-6)，c=(2,1)，所以

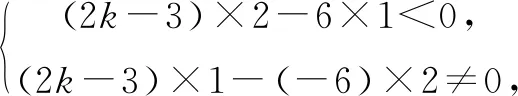
解法2 2a-3b=(2k-3,-6)，c=(2,1)，记2a-3b与c的夹角为θ，故

由题意θ为钝角，所以cosθ∈(-1,0)，

由cosθ<0，得k<3.①

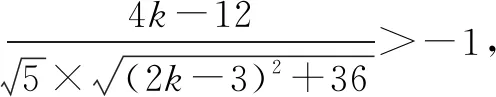
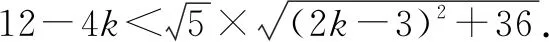
在①的前提下两边平方整理得4k2+36k+81>0，即(2k+9)2>0，得

点评如何用数来刻画钝角？可用cosθ∈(-1,0)，其中θ为两个向量的夹角，由于cosθ需要用分式表示，使得不等式“cosθ>-1”的求解相对麻烦.考虑余弦函数的有界性，只需在cosθ<0的基础上去掉“cosθ=-1”，而“cosθ=-1”等价于两个向量方向相反，而两个向量方向相反是两个向量共线的一种情况，对于两个向量的共线关系可用向量共线定理来解决，通过差集就可以把该问题转化为整式运算.这就是解法1优于解法2的原因.归纳一下两个向量的夹角为锐角或钝角的求解方式：①a与b的夹角为锐角⟺a·b>0且a与b不共线；②a与b的夹角为钝角⟺a·b<0且a与b不共线.

例3 设a，b，c是单位向量，且a·b=0，则(a-c)·(b-c)的最小值为( ).

解法1 因为a，b是单位向量，且a·b=0，在平面直角坐标系中取a=(1,0)，b=(0,1)，又c是单位向量，设c=(cosθ,sinθ)，θ∈[0,2π].

a-c=(1-cosθ,-sinθ)，

b-c=(-cosθ,1-sinθ)，

(a-c)(b-c)

=(1-cosθ,-sinθ)·(-cosθ,1-sinθ)

=-cosθ(1-cosθ)-sinθ(1-sinθ)