巧用“裂项”构造导数定义求不定式极限

纪定春

(四川师范大学数学科学学院 610068)

一、导数定义与不定式极限简介

导数是高中重要的知识模块,是高中数学学习的重点和难点.目前，大部分高中数学教师并不重视对数学概念的教学，正如章建跃先生所讲：“当下的概念课教学多是一种走‘形式化’的过程，以解题教学代替概念教学的现象比较普遍.”不仅仅是数学概念的教学已经“形式化”，而是对数学本质的学习已大幅度削弱，如对数学中的定义、定理、命题、推理等的学习.大部分的数学教学都是知识讲解与解题训练相结合，这对短期内提升学生学习成绩是有意义的，但是从长远来看，势必会严重阻碍学生数学思维的发展，应该值得深思.接下来，将对导数的定义和不定式极限作简单的介绍.

导数定义设函数y=f(x)在x=x0处的瞬时变化率为

则称它是函数y=f(x)在x=x0处的导数，记作y=f′(x0)，即

这就是函数定义在点x=x0处的导数.

不定式极限若函数f和g满足：

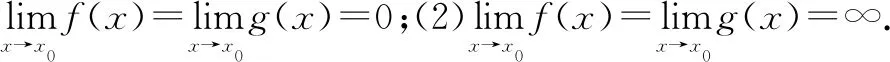
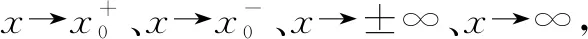
二、巧用“裂项”构造导数定义求不定式极限

1.含参数恒成立问题

例1(2016年四川高考理科卷第21题)设函数f(x)=ax2-a-lnx，其中a∈R.

(1)略；

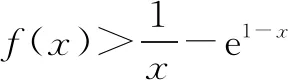
解析问题(1)解答，略.

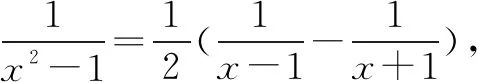
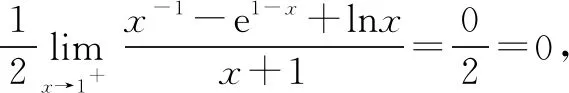
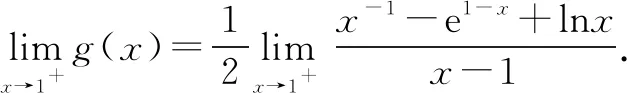
令h(x)=x-1-e1-x+lnx，显然h(1)=0.

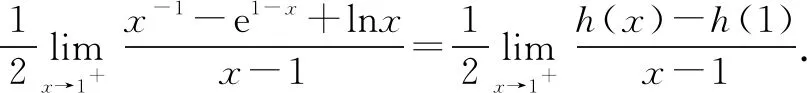
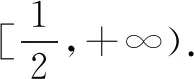
评注该方法是巧用“裂项”法，将极限为零的分式结构裂项，把原极限问题转化成正常极限和导数的定义，通过导数定义将分式结构极限问题专化成整式极限问题，利用导数定义作为桥梁，建立分式极限与整式极限之间的关系，充分体现了化归与转化思想.

2.求参数的最值问题

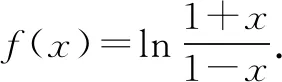
(1)略；(2)略；

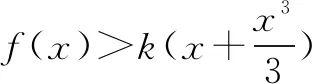
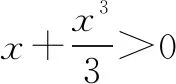
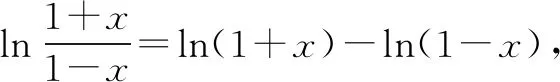
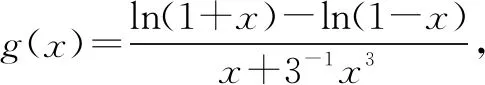
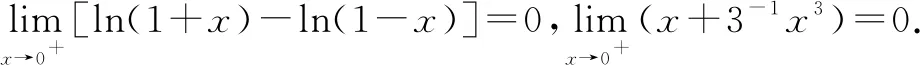
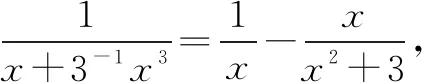
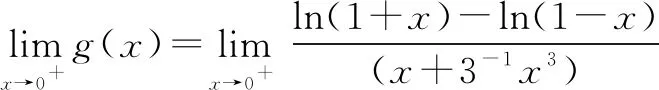
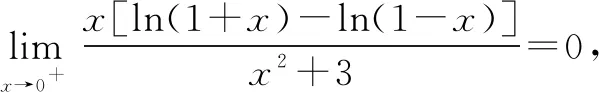
令函数h(x)=ln(1+x)-ln(1-x)，则有h(0)=ln(1+0)-ln(1-0)=0.

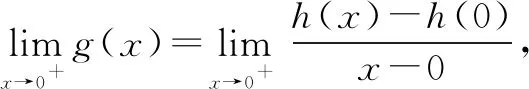
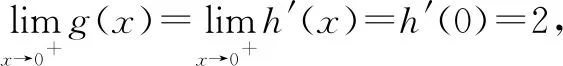
评注该方法巧用“裂项”法，将分母结构裂成两项之差，然后构造导数定义，把不定式(分式)极限问题转化成整式极限问题，展现了导数定义在求不定式极限问题中的重要作用和地位，充分地体现了化归与转化思想.

3.求参数的取值范围

例3(2015年山东理科数学第21题)设函数f(x)=ln(x+1)+a(x2-x)，其中a∈R.

(1)略；(2)若∀x>0，f(x)≥0成立，求a的取值范围.

解析问题(1)解答，略.对于问题(2)，对∀x>0，f(x)≥0成立，等价对任意x>0，ln(x+1)+a(x2-x)≥0恒成立.考虑分离参数a，则需分类讨论.

当x=1时，显然有ln2+a(1-1)=ln2≥0，即a∈R.

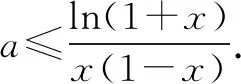
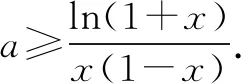
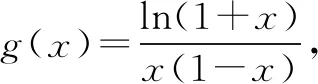
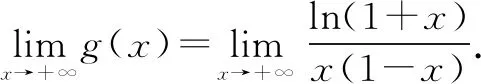
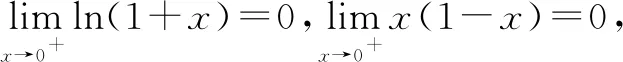
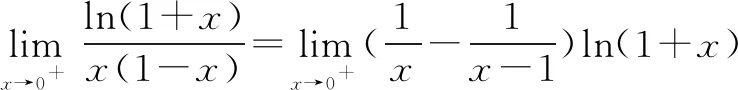
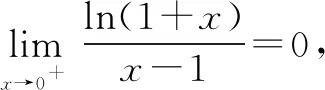
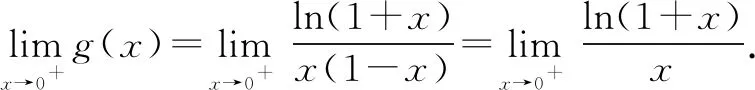
令h(x)=ln(1+x)，则h(0)=ln(1+0)=0.

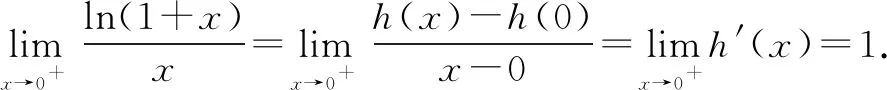
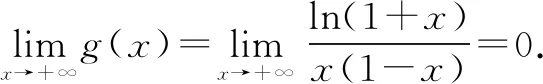
综上所述，参数a的取值范围为[0,1].

评注该方法巧用分类参数法和“裂项”法，将一个不定式极限问题转化成可求极限的导数定义问题，降低了思维的难度，同时也说明高中数学教学要注重概念的教学.

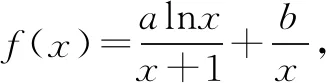
(1)略；

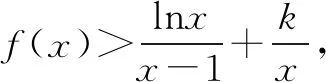
解析问题(1)解答，略.对于问题(2)，由问题(1)可知，a=1，b=1.

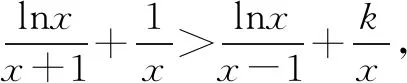
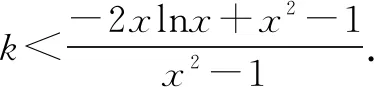
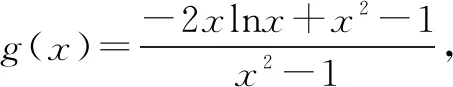
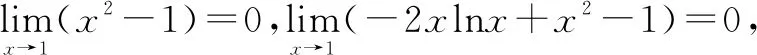
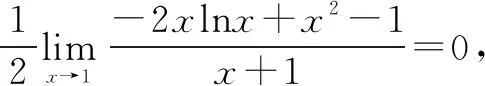
令g(x)=-2xlnx+x2-1，可得g(1)=0.

综上所述，k的取值范围为(-∞,0].

评注该方法先分离参数，再用“裂项”法将不定式极限转化成导数的定义，最后利用导数的定义将一个分式极限转化成整式极限.

李邦河院士在获得华罗庚数学奖的报告中就指出：“数学玩的是概念，而不是纯粹的技巧.”在一些难题、技巧上下功夫，是一种舍本逐末的做法.数学概念作为学生数学生长发育的细胞，是建构数学大厦的基础.数学概念的教学，是培养学生数学生长发育“干细胞”的教学，因此数学教学应该是注重数学概念的教学.导数的概念教学，要深度地剖析导数的定义内涵与外延、导数定义的构成要素、导数定义的结构等，让学生深刻地理解导数的几何意义与代数形式.

数学概念的教学应该是注重培养学生数学思维的教学，是数学方法、思想、精神的深度教学，而不是走“形式化”的解题教学.正如著名的数学家米山国臧所说：“纵然把数学知识忘记了，但数学的精神、思想、方法也会深深地铭刻在头脑里.”数学知识是具体化的数学思想，数学思想方法是数学中的精华部分，掌握了数学的方法、思想和精神也就统领了数学知识.例如，在导数定义的教学过程中，应当让学生体会分割的思想、极限(逼近)的思想、整体到局部的思想、从特殊到一般的思想等，让学生的思维方式由静态向动态转变，感受无限的魅力，进而促进学生数学思维的发展.