非同心型挤压油膜阻尼器空化流场特性数值模拟

崔颖， 王清智， 王永亮， 李婷

(大连海事大学 船舶与海洋工程学院，辽宁 大连 116026)

挤压油膜阻尼器(squeeze film damper，SFD)作为轴系的减振元件，具有体积小、结构简单、减振效果明显等优点，广泛应用于航空和舰船燃气轮机轴系减振结构中。SFD结构分为同心型和非同心型，由于非同心型阻尼器结构中内环重力载荷没有弹支结构来平衡，阻尼器的内环与外环存在静态偏心距。相比之下，非同心型阻尼器内的流动与减振特性较同心型挤压油膜阻尼器更为复杂，掌握其空化流场特性可为对其减振特性分析奠定基础。

挤压油膜阻尼器普遍存在气穴现象，气泡的生成、发展和溃灭会对SFD的油膜压力分布产生较大程度的影响。国内外学者对阻尼器的气穴现象做了大量的研究，传统的求解方法是基于单相流的J-F-O模型，认为正压区均为液相，负压区均为气相，采用Elrod算法确定油膜的边界[1-3]。White[4]通过实验发现当内环的进动偏心距较大时，高压区仍会出现气泡，这表明传统的求解方法存在不足。Zeidan等[5]和Vance等[6]应用高速摄像技术观察到阻尼器在高速工作过程中所形成的气穴为吸入空气和滑油蒸汽的混合物，因而有必要在挤压油膜阻尼器建模中对不同的空化类型和机制进行区分。针对两端开口型SFD，Diaz等[7]最先把气泡动力学(Rayleigh-Plesset，R-P)方程的引入到SFD的空化问题研究中，不考虑R-P方程的惯性项、阻尼项和表面张力项，提出了一种考虑从外界吸入空气的空化模型。Someya[8]在R-P方程中引入了气泡表面的膨胀黏度，补充并完善了Diaz 在研究时所采用的简化形式的R-P方程。Gehannin等[9]提出将完全R-P方程应用于油蒸汽空化现象预测中，并分析了R-P方程中各个因素对SFD流场特性的影响。以上研究中所采用的空化模型，都是建立在雷诺方程的基础上。若所求解的SFD的物理模型稍加复杂，则会存在一定程度的不足。

近年，计算流体力学(computational fluid dynamics, CFD)软件的快速发展使得一些学者开始利用它来对SFD的流场特性深入计算分析[10-13]，CFD软件所包含的丰富计算模型和方法可对空化流场进行精确求解，并且建立的物理模型不受几何结构限制。本文针对文献[14]中所采用的非同心型SFD结构，利用Mixture多相流模型、Z-G-B空化模型和动网格技术，通过Fluent软件中的用户自定义函数UDF(user-defined function)编辑SFD内环进动频率和半径，从而对流场不同时刻压力分布和空化特性进行数值研究，利用实验结果对数值模拟结果进行了验证。

1 阻尼器流场的数值建模

1.1 阻尼器三维建模

采用Gambit软件对文献[14]中的非同心型SFD结构进行三维建模，SFD的结构示意如图1所示。

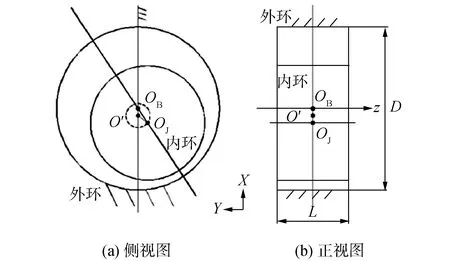
图1 SFD结构示意[14]Fig.1 Schematic diagram of SFD[14]

阻尼器的结构参数为：外环直径D=140 mm，径向间隙C=0.385 mm，静偏心距d=0.016 mm，轴向长度L=30 mm。进油和出油均是轴向方向，基于文献[14]中的第2组实验(Ⅱ run)的工况进行边界条件设置，并将后续的计算结果与实验结果作对比。设置出口压力是环境大气压，进油压力选取不同的值，润滑油的动力黏度μ=0.066 Pa·s。

将阻尼器外环圆心设为坐标轴原点，阻尼器轴向方向为Z轴方向，Z轴负方向进油，正方向出油，该阻尼器的三维模型关于XY面对称，如图2所示。阻尼器的外环定义为静止壁面，利用Fluent软件中的UDF对内环进动频率和半径进行编辑。

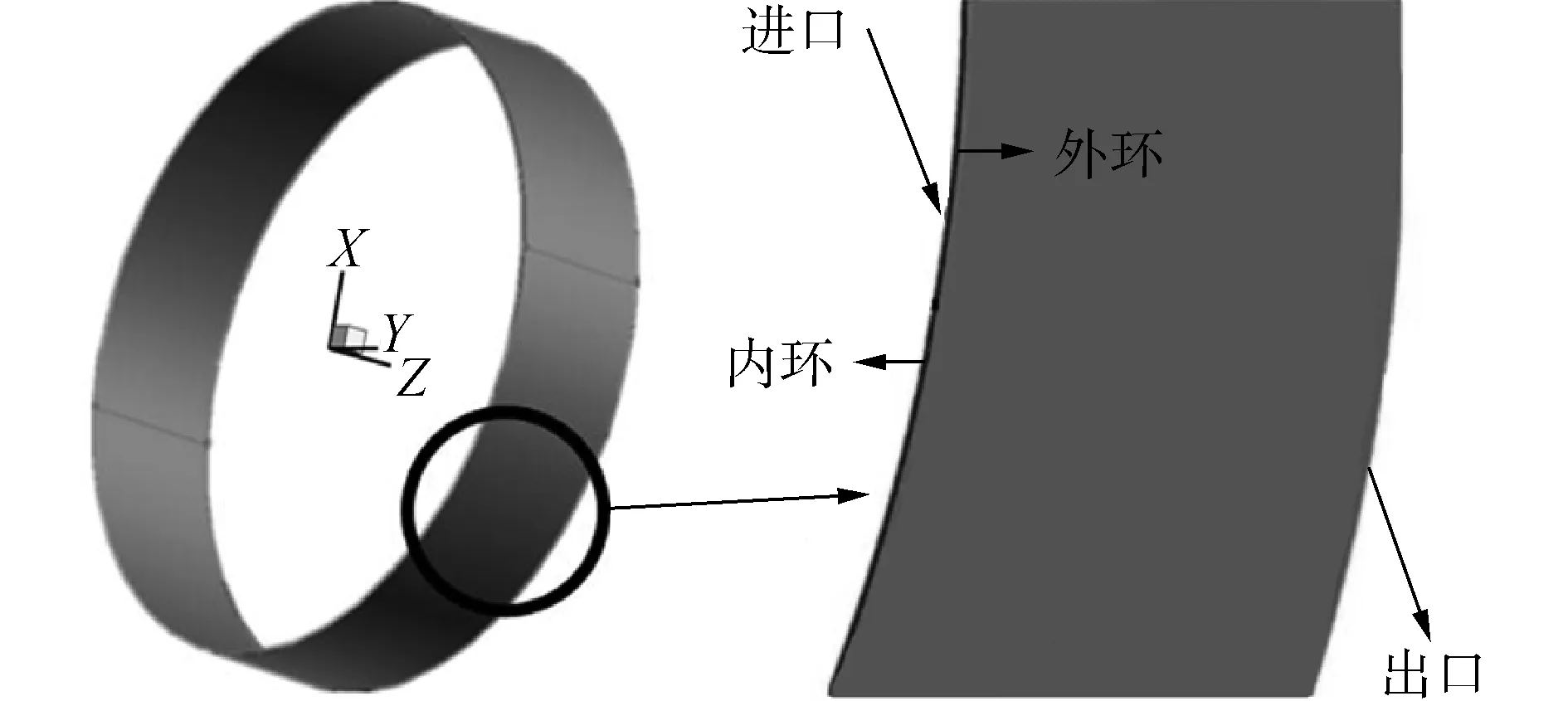
图2 SFD三维模型及边界定义Fig.2 Three-dimensional model and boundary definition of SFD

1.2 多相流模型

Fluent软件中Mixture模型是一种简化的多相流模型，通过对连续方程和动量方程的求解，再结合相对速度方程以及气体体积分数方程来模拟多相流动，具有较高的收敛性，故选取该模型来进行模拟。为研究方便，假设液相和气相位均匀混合状态，均不可压缩，在靠近壁面处流体无滑移，并且不考虑相间的相对速度和滑油黏度的变化。其控制方程为：

(1)

(2)

(3)

∂(ρmvm)/∂t+·(ρmvm)=-p+

(4)

式中：ρv是气相的密度；ρl是液相的密度；ρm是混合相的密度；V是气相的速度；Re和Rc分别是气体生成和凝结的速率；αv是流场中气相体积分数；vm是质量平均速度；F为体积力；μm是混合相的动力黏度；p是压力。

1.3 空化模型

采用Z-G-B空化模型来求解气泡的蒸发和凝结，其忽略流体中的不可凝结气体，假定全部气泡尺寸相同，利用气泡的密度数(n)来求解单位体积内总的相间质量传递率(R)，其表达式为：

(5)

根据广义Rayleigh-Plesset方程推导出气泡动力学方程：

(6)

式中：RB为气泡半径；PB为气泡表面压力；P为当地远场压力；ρl为液相密度；S为液体表面张力系数。

若忽略二阶项与表面张力项，上式可简化为：

(7)

将方程(5)与方程(7)联立并结合气相体积分数，可得：

(8)

若要将其应用于气泡凝结过程，引入下式：

(9)

式中：F为经验校准系数，考虑当气泡体积分数增加，成核位置的密度减小，用(1-αv)αnuc来替换原有的气相体积分数，可得：

当P≤Pv时：

(10)

当P>Pv时：

(11)

式中：气泡的半径RB=1 μm，在成核位置处的体积分数αnuc=5×10-4，蒸发系数Fvap=50，凝结系数Fcon=0.01。在计算过程中本文将空化压力取为绝对压力0。

1.4 动网格模型

选取动网格模型中弹簧光顺法(smoothing methods)，当边界处的网格发生变形时，内部的网格结点也随之变形，而结点数目和连通性维持不变，结点位置的更新方程为：

xnew=xold+uΔt

(12)

本文选择Diffusing模型控制网格的变化，该模型能使网格在运动过程中保持较高的质量，控制网格形变的扩散方程为：

·(γu)=0

(13)

式中：γ是扩散系数；u表示网格移动的速度。

1.5 无关性验证

兼顾计算机计算精度、计算速度以及计算的收敛性，需对网格数量进行无关性验证，从而选取一个最佳平衡点。采用六面体单元对流场进行网格划分，将网格数量分别设置为10万、25万、50万、75万和100万，对一个周期内内环所受的油膜力最大值进行比较，如图3所示。

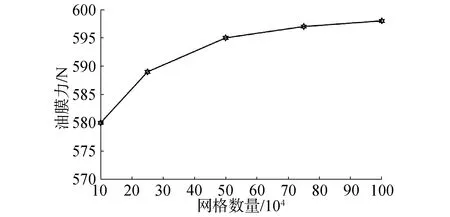
图3 不同网格数量下的油膜力Fig.3 Oil film force under different grid numbers

可以看出，当网格数量大于50万，随着网格数量上升油膜力升高幅度变缓，因此后续计算均采用50万的网格数量。其中，在阻尼器的周向布置2 000个结点，在阻尼器的轴向布置50个结点，在阻尼器的油膜厚度方向上布置5个结点。

2 阻尼器空化流场的数值分析

数值模拟了不同时刻下随着内环进动阻尼器流场油膜压力与气相体积分数分布，气相体积分数为流场单位体积中气相所占的体积比，并分析了进油压力对流场油膜压力与气相体积分数的影响。

2.1 空化流场压力与气相体积分数的瞬态分布

将阻尼器静偏心的位置与内环进动的起始位置均设置在X轴负方向，通过UDF功能设置内环沿逆时针方向进动，进动频率为50 Hz，进动半径为0.192 5 mm，进油压力为相对压力0.02 MPa，截取内环分别运动到1/4周期、1/2周期、3/4周期和1个周期时刻下的压力与气相体积分数分布云图，如图4所示。

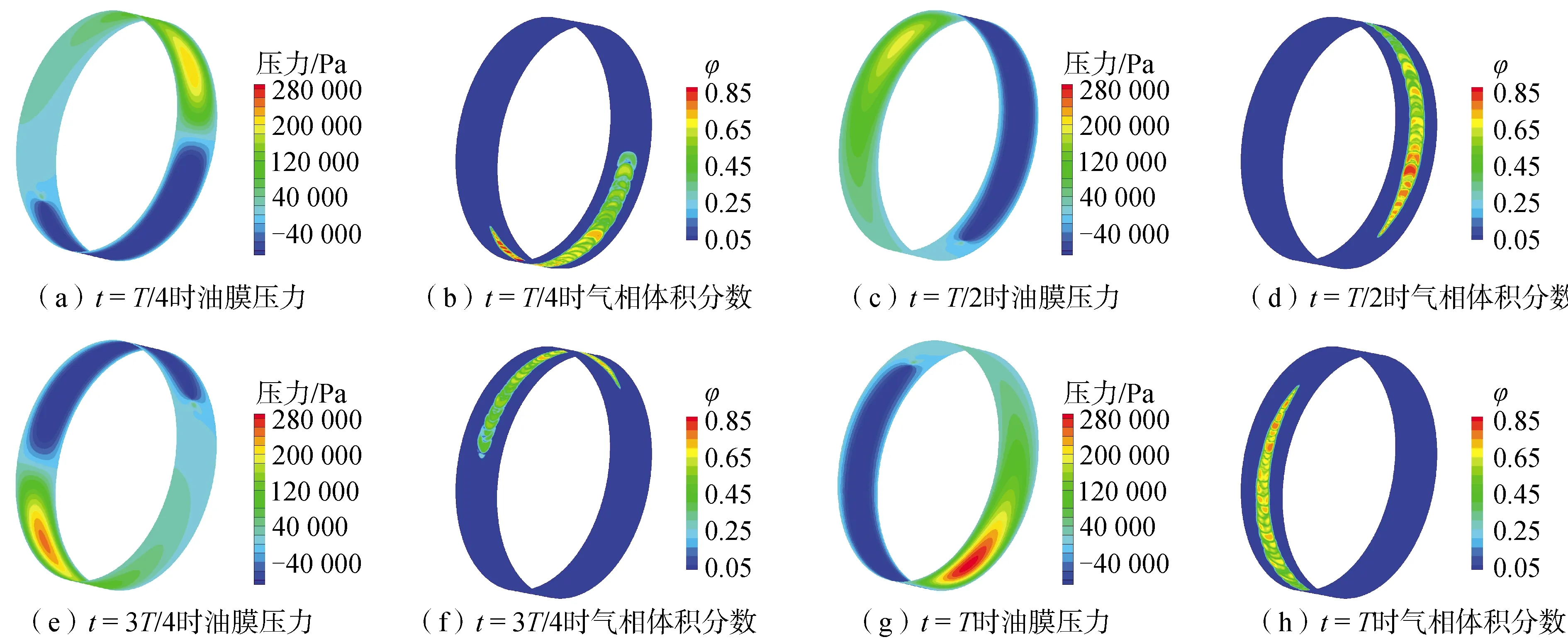
图4 不同时刻油膜压力与气相体积分数分布Fig.4 Distributions of oil film pressure and gas-phase volume fraction at different times

可以看出，随着内环进动，在油膜厚度最小处的前方产生了高压区，后方出现低压区且有气泡生成，在低压区的中间位置存在条状气相带，其宽度沿内环进动方向逐渐减小，高压区域的范围和油膜压力峰值以及压力梯度均在瞬时变化。

由于静偏心的存在，在不同时刻内环对油膜的挤压程度不同，油膜压力和气相体积分数随之变化。如在t=T时刻，内环运动到X轴负方向，此时油膜厚度最小，高压区油膜压力达到最大；在t=T/2时刻，内环运动到X轴正方向，此时油膜厚度最大，高压区油膜压力达到最小。气穴比为气相体积占整个阻尼器内流场体积的百分比，其在一个周期内变化情况如图5，由于油膜压力的不断变化，不同时刻整个流场中油膜压力低于空化压力的部分随之变化，因此，滑油空化所产生的气体占整个流场的气穴比周期性变化。

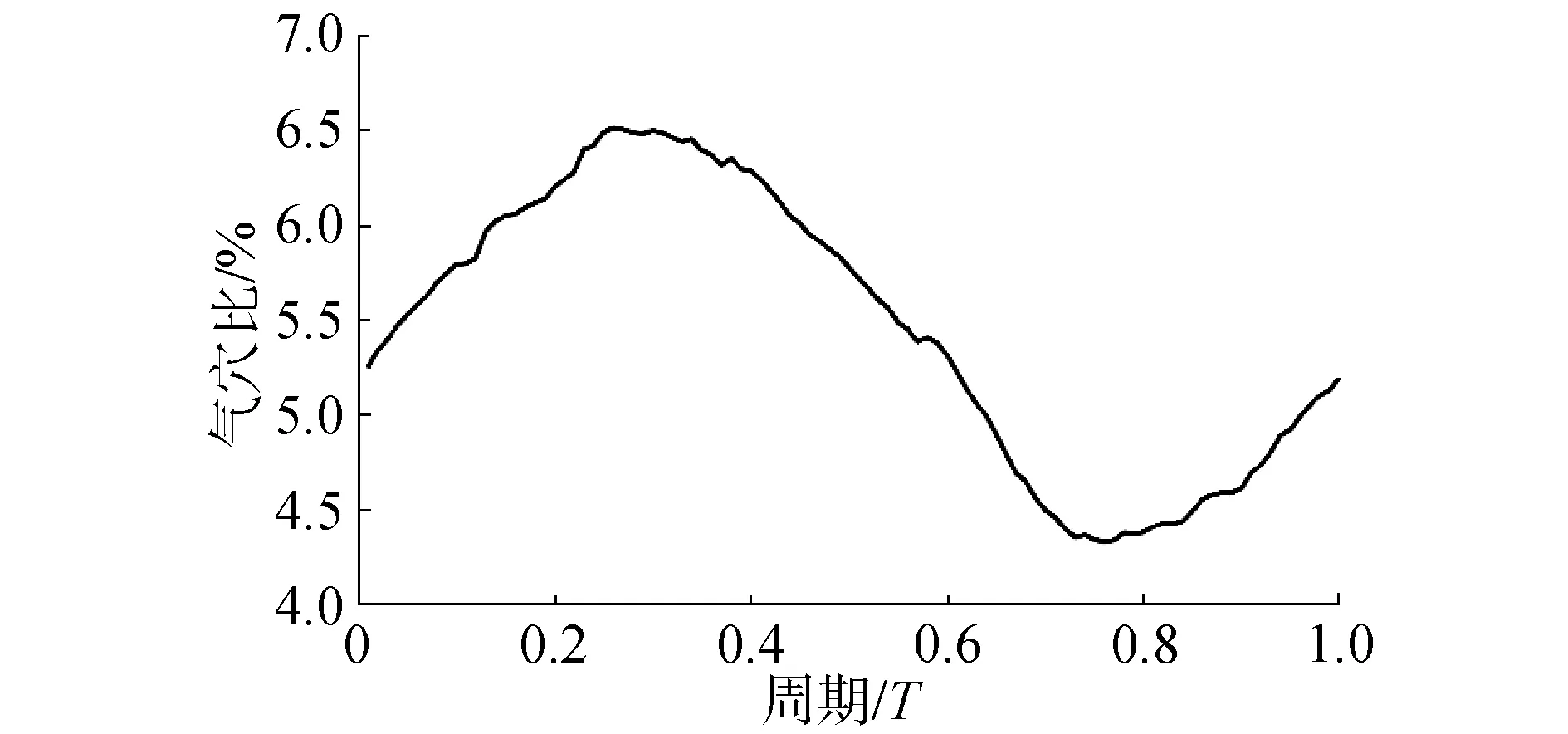
图5 气穴比变化Fig.5 Variation of cavitation ratio

2.2 进油压力对空化流场的影响

对阻尼器的进油压力Pi分别为相对压力0.2、0.5、1.0和2.0 bar条件下该阻尼器的压力与气相体积分数分布进行了计算模拟。为对比方便，将t=3T/4时刻的三维云图在Y轴负方向处裁开并延展为二维云图，向上方向为Z轴正方向，即下方为进油边、上方为出油边。图6给出了不同进油压力下阻尼器油膜压力与气相体积分数分布。可见，随着进油压力不断升高，高压区范围的压力值逐渐增大，低压区范围不断缩小。并且条状气相带的范围和气相体积分数随进油压力增大而不断减少。另外，当进油压力较小时，高压区和低压区处于轴向的中间位置，随着进油压力不断升高，阻尼器进出口压差对空化流场的影响越来越大，导致高压区逐渐向进油边移动，低压区逐渐向出油边移动。

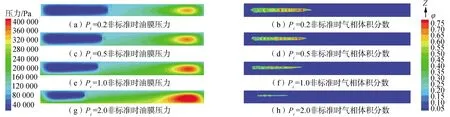
图6 不同进油压力下的油膜压力与气相体积分数分布Fig.6 Distributions of oil film pressure and gas-phase volume fraction under different supply pressure

3 数值模拟与试验结果对比分析

根据文献[14]中的实验监测点布置，下面对这3个监测点处的油膜压力与气相体积分数的变化规律进行分析。选取轴向的中间位置即Z=0平面，在外环上布置3个监测点TP1、TP2和TP3，其相对位置如图7所示。

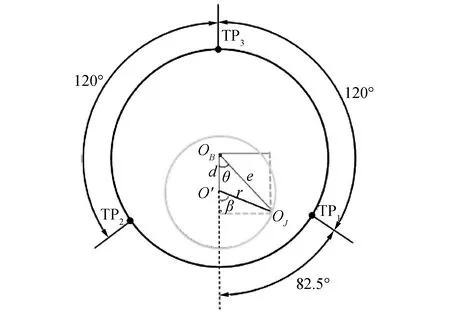
图7 监测位置示意[9]Fig.7 Diagram of monitoring location[9]

针对3个测点的油膜压力变化规律进行分析，分别设置进油压力为相对压力0.2和2.0 bar，得到各监测点处的油膜压力关于内环进动角度β的变化规律，并与实验结果作对比。通过几何关系推导出各个监测点处的油膜厚度关于内环进动角度的变化，进一步分析油膜压力与油膜厚度之间的关系，如图8所示。

由图8可知，由于3个监测点在布置上彼此相差120°的相位，所以其压力变化曲线也各有120°的相位差，且由于径向间隙不同，各个监测点的油膜压力的峰值也不相同。油膜压力在上升阶段为缓慢上升过程，下降阶段为迅速下降过程。随着进油压力由0.2 bar增大到2.0 bar，监测点油膜压力随之上升，但在下降阶段曲线基本重合，且当监测点处于阻尼器内压力场的低压区时，由于增大了进油压力，低压区的压力得到补偿，因此压力曲线的低压区域逐渐变窄。从油膜压力曲线与油膜厚度曲线之间的关系可以看出，在油膜厚度达到最小之前压力已达到最大值，当油膜厚度为最小值时压力接近于空化压力。本文采用的Z-G-B空化模型在油膜压力低于给定空化压力时产生空化现象，因而通过数值方法得到的压力曲线在低压区的压力峰值以及持续时间与实验结果略有不同，表明所采用的空化模型与实际的空化现象仍存在一定的偏差。但总体来看，油膜压力的数值仿真结果与实验结果基本一致。

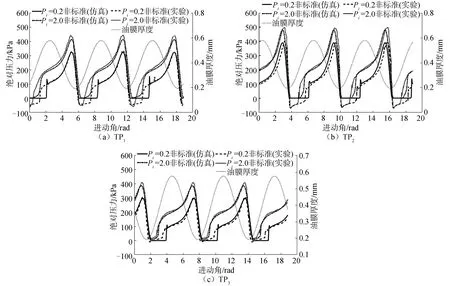
图8 不同监测位置油膜压力的计算结果与实验数据对比Fig.8 Comparisons of numerical and experimental data of oil film pressure at different monitoring locations

在此基础上，进一步数值模拟分析各个监测点气相体积分数的变化规律及其与油膜压力之间的关系，在进油压力为0.2 bar的条件下，对3个监测点的油膜压力与气相体积分数进行分析，如图9所示。

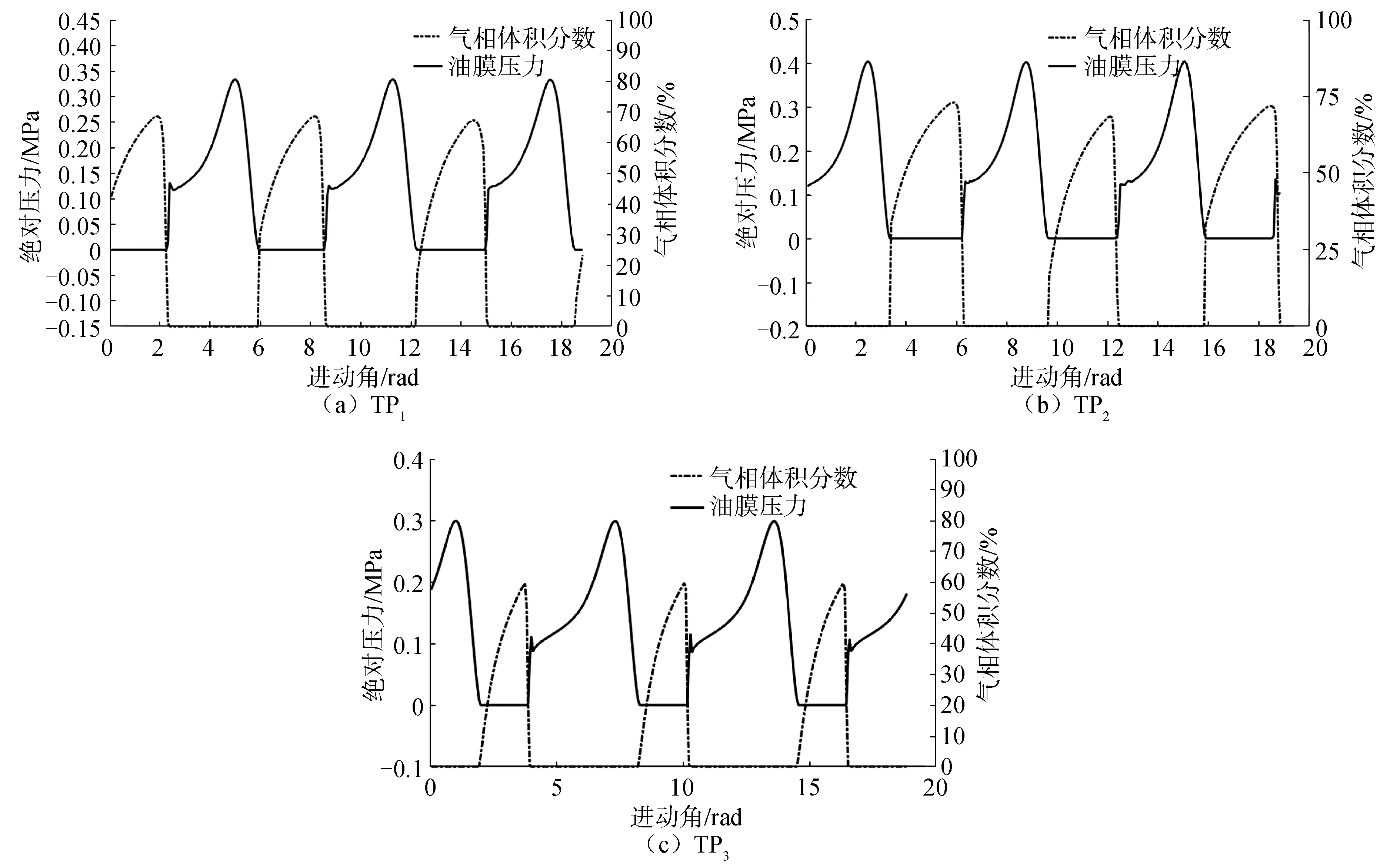
图9 不同监测位置油膜压力与气相体积分数的瞬时变化Fig.9 Instantaneous variations of oil film pressure and gas-phase volume fraction at different monitoring locations

由于3个监测点处的最小油膜厚度不同，因而各处在产生空化时的气相体积分数随最小油膜厚度的增大而减小。随着内环进动，对比3个监测点处的油膜压力变化曲线和气相体积分数变化曲线可知：当油膜压力低于空化压力时出现气泡，气泡的生成过程是较为缓慢的过程；随着监测点处的油膜压力不断升高，当其高于空化压力时气泡开始减少直至全部消失，气泡的溃灭过程相比于气泡生成过程更为迅速。

4 结论

1)基于Mixture多相流模型、Z-G-B空化模型和动网格技术建立了非同心型挤压油膜阻尼器三维非定常空化流场求解模型，数值模拟得到由于各个不同时刻内环对油膜挤压程度不同，使得油膜压力与气相体积分数分布和阻尼器流场中的气穴比随内环进动而瞬时周期性变化。

2)数值模拟发现该型阻尼器的进油压力对流场的压力分布和气穴比影响显著，进油压力增大使得油膜高压区域范围增大，油膜压力峰值及压力梯度增大，而低压区缩小，气穴比减少；并且随着进油压力的增大，流场内高压区向进油边移动，低压区向出油边移动。

3)通过对阻尼器外环监测点瞬时油膜压力计算结果与文献中的实验结果进行对比，表明各监测点的模拟结果与实验基本吻合，验证了本文所采用的挤压油膜阻尼器流场数值模拟方法具有较高的精确性，可用于更复杂结构的挤压油膜阻尼器空化流场的预测分析。