水下球体目标散射声场相位特性
周彦玲, 范军, 王斌
(上海交通大学 高新船舶与深海开发装备协同创新中心,海洋工程国家重点实验室,上海 200240)
传统的主动声呐系统中,水下目标声散射回波的相位信息往往被忽略,主要研究回波的强度。随着水下目标声散射特征精细化研究的需求和发展,特别是利用主动声呐系统进行目标探测、识别[1],精确声制导以及潜艇主动消声隐身技术的发展,相对以往仅仅对声散射强度的重视,目标声散射相位特性逐渐受到关注。论文针对水下目标声散射相位计算、提取方法开展理论和实验研究,具有重要的理论价值和工程应用前景。
Mitri等[2]介绍了利用传统傅里叶变换提取目标共振散射形态函数相位的方法,但对窗函数的要求很严格。Rayleigh简正级数解的解析方法只能求解少数规则形状目标的声散射相位,为实现复杂目标声散射相位计算,论文提出基于有限元方法的水下目标声散射相位的数值计算模型。以COMSOL Multiphysics软件为计算平台,求解弹性球和单层球壳目标的频域形态函数并进行时域回波仿真,再利用全相位法[3]提取回波相位,得到了和Rayleigh简正级数解相吻合的结果,直接说明了有限元方法是准确、有效的。而已有的研究证明全相位法具有“相位不变性”、无需附加的频率估计和频谱校正措施、精度较高、更优良的抑制频谱泄漏的优势,可应用于回波相位提取。最后开展了单层球壳反向散射实验,利用全相位法获取了其声散射相位特性,与理论预报结果相比吻合较好。
1 水下球体目标声散射相位的计算方法
1.1 基于Rayleigh简正级数解的声散射相位计算
以刚性球为例,推导其声散射场的经典Rayleigh简正级数解,获得其形态函数相位特性随频率和空间位置变化规律。如图1所示,球体半径为a,设单位振幅的简谐平面声波沿+z轴方向入射到球,省略时间因子exp(-iωt)。
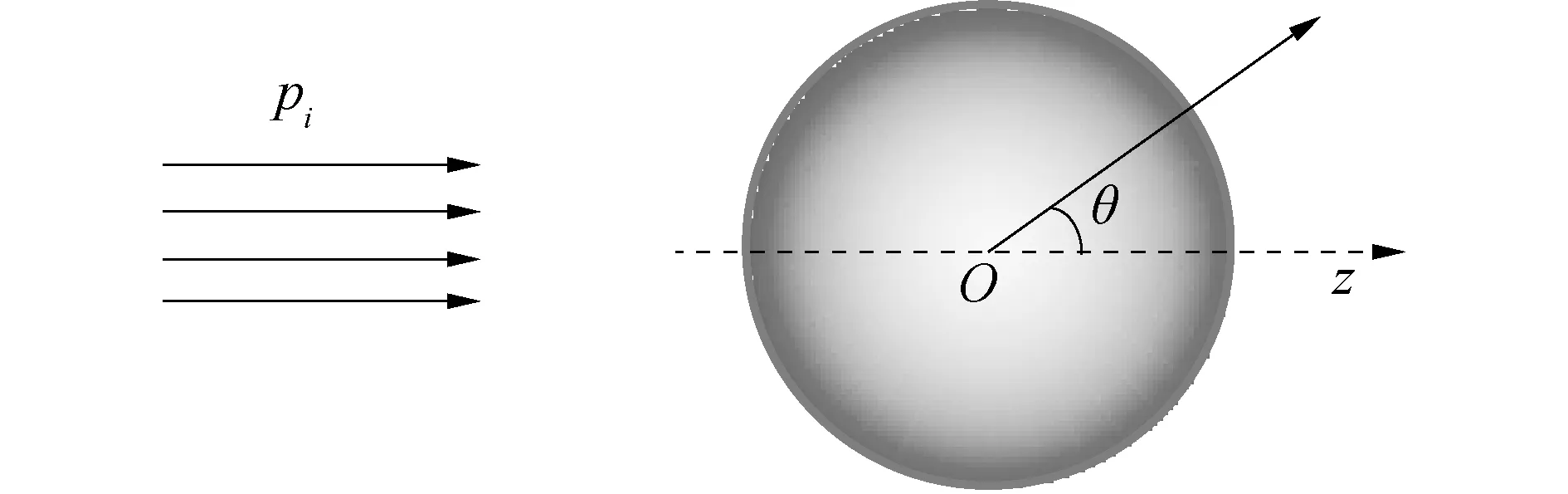
图1 刚性球的散射Fig.1 Scattering of the rigid sphere
入射波可表示为:exp(ikz)=exp(ikrcosθ),显然与方位角φ无关,只依赖于俯仰角θ。将入射平面波按球面波展开:
pi(r,θ)=exp(ikrcosθ)=
(1)
式中:Pn(cosθ)是n阶Legendre函数,jn(kr)是n阶球Bessel函数。
同样,散射波声场可表示为:
(2)
式中:hn(1)(kr)为第一类球Hankel函数,an是待定的散射系数。根据边界条件可以计算得到散射系数an[4-5],不同球形结构目标对应的散射系数an不同,定义形态函数为:
(3)
式中x=ka为无因次变量。式(3)排除了目标相对距离(a/r)和传播相位延迟的影响,它与观察点方位角θ有关。当θ=π时,得到反向散射形态函数f(x,π)。图2给出了不同频率平面波激励下刚性球表面散射声场相位分布。
图2 刚性球表面散射声压相位分布Fig.2 Phase distribution of surface scattering sound pressure for the rigid sphere
从图2可以看出:刚性球表面散射声压相位沿波入射方向呈现周期交替变化;频率越低,声波波长越长,这种周期交替节线越少,表示相位变化缓慢,频率越高,声波波长越短,这种周期交替节线越多,表示相位变化剧烈;若进行主动消声隐身,由于目标低频声散射相位变化缓慢,更容易实现整体消声,高频相位变化剧烈,对于整体主动消声是困难的,但可以进行局部消声处理。
基于Rayleigh简正级数解计算不同频率平面波激励下刚性球、弹性球散射声场的相频特性曲线,刚性球、弹性球半径均为1 m,计算用材料的基本声学参数见表1。

表1 材料的基本参数Table 1 Parameters of materials
由图3(a)、(b)可以看出:刚性球、弹性球相频特性不同,刚性球在ka>2π时相位随频率变化呈现周期性,并且在每个周期内接近线性变化,但是在较低ka情况下,其相位呈现不同的变化规律,不再接近线性变化。弹性球由于出现弹性波共振,随频率变化不再具有线性,特别是在弹性波共振频率处出现相位的跳变现象,这为利用相位信息进行目标识别提供可利用特征。

图3 形态函数相频特性Fig.3 Phase-frequency curves of the form function
图4(a)、(b)给出了不同壳厚、不同材料弹性球壳在收发合置情况下散射形态函数相位随ka变化规律,球壳内部真空,所用材料为钢。图4(a)显示:不同壳厚的球壳呈现的相位变化特性存在较大差异。当壳很薄时,仅仅是最低零阶广义对称与反对称Lamb波共振出现,在少数频率点存在相位跳变,其他频率基本接近刚性球情况;当壳逐渐变厚,其他高阶的广义对称与反对称Lamb波共振也出现了[6],因此跳变频率点增加,也越来越接近弹性球的情况。图4(b)中不同材料的弹性球壳,共振峰频率存在差异,导致相位跳变的频率不一致,可以利用此特征对不同材料进行识别。
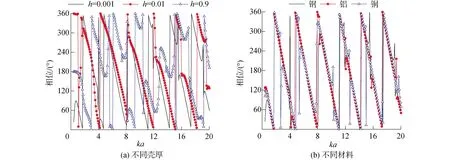
图4 不同厚度、材料弹性球壳的相频特性Fig.4 Phase-frequency curves of the elastic spherical shell with different thickness and materials
1.2 基于有限元声散射相位计算
基于COMSOL Multiphysics软件,采用有限元方法建立弹性球和弹性球壳散射声场相位数值计算模型[7](见图5)。计算其背向散射形态函数的相频特性,并与Rayleigh简正级数解对比,建模的基本参数:球体外径1 m,内径0.999 m,材料为钢。

图5 定义物理场及求解域Fig.5 Definition of acoustic scattering field and solving domain
图6中数值计算结果和解析计算结果对比显示:基于有限元数值计算方法结果和Rayleigh简正级数解的计算结果吻合较好。由此证明,有限元方法可以用来计算水下目标中低频声散射相位特性。
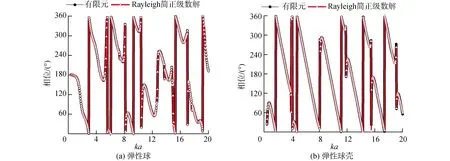
图6 有限元和Rayleigh简正级数解对比Fig.6 Comparison of the finite element method and Rayleigh normal mode solution
2 散射声场相位的提取方法
下面以单频复指数序列x(n)=exp(i(2πnm/N+θ0))为例,分析其传统FFT谱和全相位FFT谱[8-10]。x(n)对应的传统FFT谱为:
(4)
x(n)对应的全相位FFT谱为:
(5)
式(4)和式(5)比较可以看出,序列{exp(i(2πmn/N+θ0)),-N+1≤n≤N-1}的全相位FFT频谱幅值等于传统FFT频谱幅值的平方,即全相位FFT方法得到的频谱主旁瓣比值较大,主瓣更集中,从而能够很好的抑制频谱泄漏。式(4)表明,传统FFT各条谱线的相位值与其对应的频率偏移m-k有关,当采样频率不是信号频率整数倍时,传统FFT频谱分析一般会导致较为严重的频谱泄漏效应。而式(5)显示,全相位FFT频谱的相位值为θ0, 即为中心样点的理论值,与频率偏移无关。因此,全相位FFT方法具有相位不变的性质。即使在采样不同步的情况下,也不需要借助附加的相位校正措施就可以精确地提取出信号的相位信息。
采用频域间接法[11]对内部真空球壳进行时域回波仿真,图7为入射波30 kHz时时域回波。球壳外径为0.1 m、厚度0.2 mm,球壳材料为钢。如图7所示,矩形线框表示选取的时间窗,截取一段稳态的直达波信号,利用全相法得到截断信号初相位,即直达波的初相位,归算到零时刻;再以同样的方法截取一段稳态的回波信号,再次利用全相位法提取其截断信号初相位,即回波的初相位,归算到零时刻;将回波相位减去直达波相位,得到目标散射声场相位。图8给出了弹性球壳时域回波仿真利用全相位的方法提取的相位与Rayleigh简正级数解的相频特性对比。
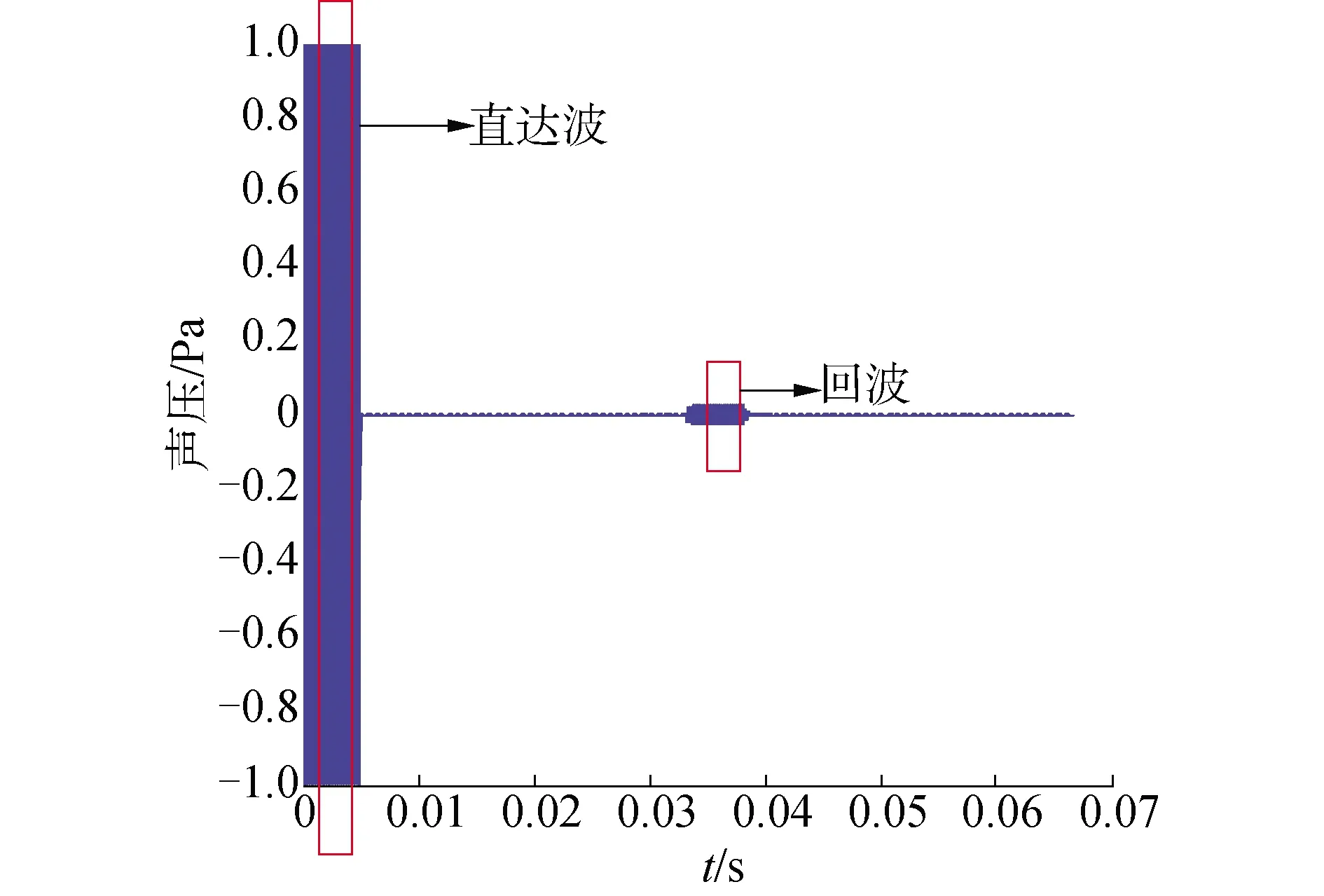
图7 理论仿真的时域回波Fig.7 Time-domain signal of simulation
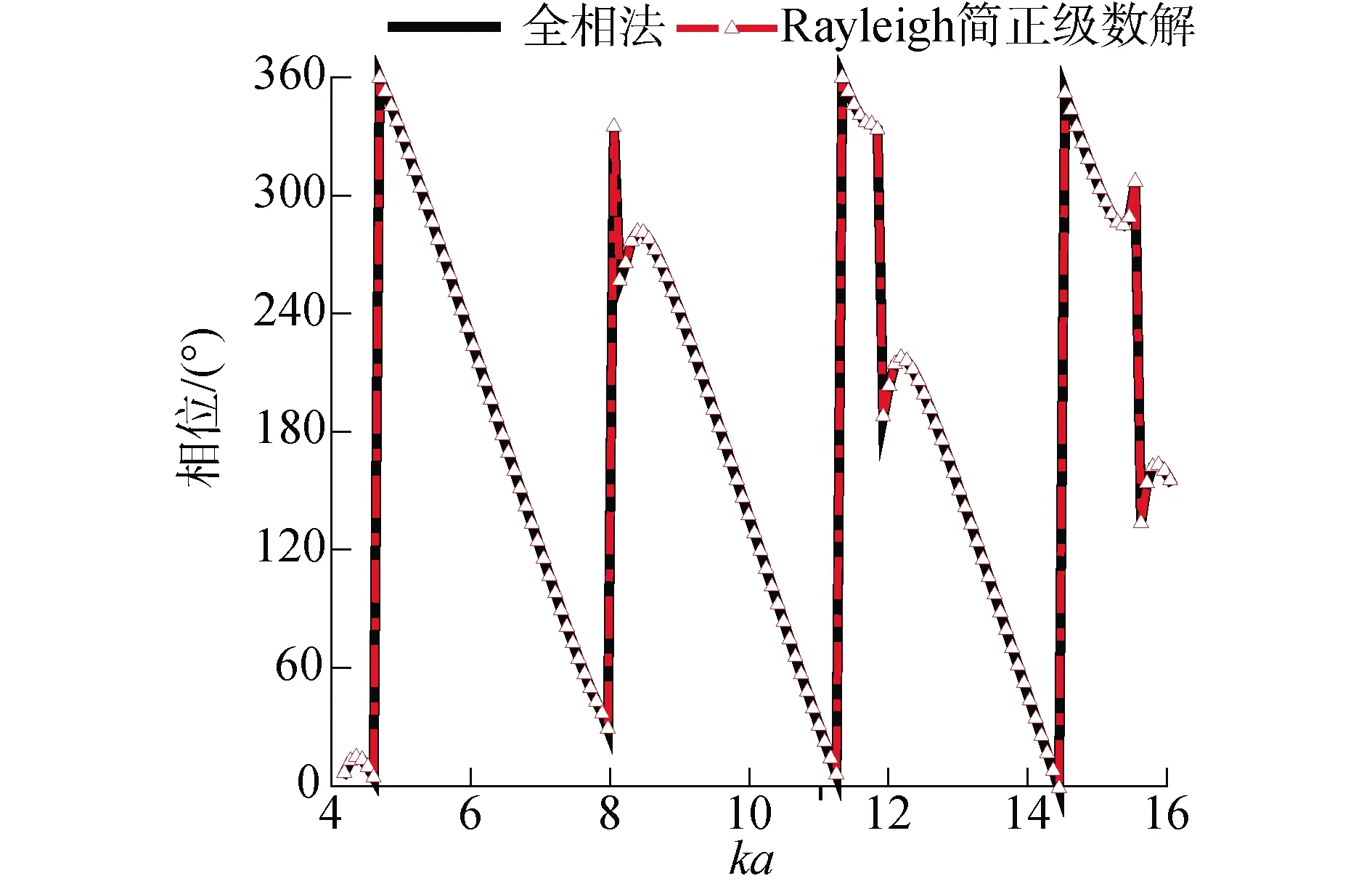
图8 回波仿真与Rayleigh简正级数解相频特性对比Fig.8 Frequency-response comparison between time-domain simulation and Rayleigh normal mode solution
与解析解对比结果显示:本文提出的利用全相位方法提取目标回波信号的相位是准确和有效的。
3 水下球体目标声散射实验
以实验的方式对上述方法进行验证,本实验在上海交通大学水声工程实验室的水池中进行,水池空间尺寸5 m×5 m×5 m。发射阵、水听器和目标三者中心位于同一直线上,距离水面1.94 m。移动目标以观察回波中目标的位置,确保目标散射回波信号介于直达声和混响之间,而不产生混叠。发射阵中心距离水听器0.94 m,目标距离水听器0.92 m。发射信号为单频脉冲信号:频率f为20~40 kHz,间隔500 Hz,脉宽为(10/f)ms。实验模型为钢球壳,外径为0.2 m。图9给出测试实验布局示意图和实验模型。
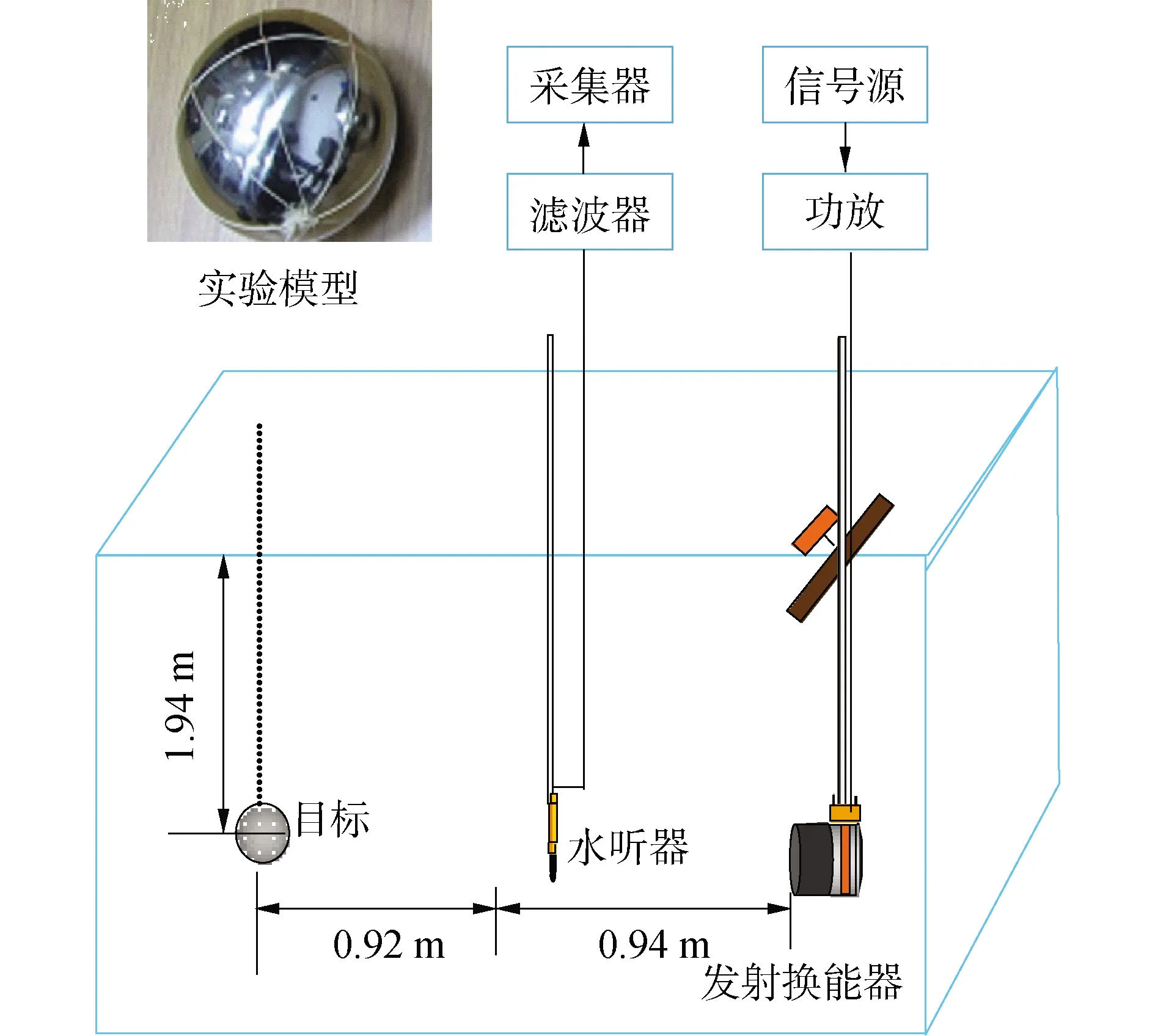
图9 实验模型和装置布放Fig.9 Experimental model and layout diagram
通过计算,直达波应该在0.6 ms附近到达,而目标回波应该在1.85 ms到达。图10为发射信号频率20 kHz时,实验采集的时域回波信号。利用全相位法提取弹性球壳散射声场的相位,将实验所得的结果与Rayleigh简正级数解的结果进行对比,如图11所示。

图10 时域回波信号Fig.10 Time-domain echo signal
图11中,对比Rayleigh简正级数解计算结果和实验结果,2条曲线基本吻合。虚线框为由于弹性波共振出现的相位跳变现象,可以看到共振峰很窄,实验测量中很难测量得到弹性共振峰。为了得到稳态长脉冲,实验测量中采用单频脉冲信号,由于测量频率点数较少,实验中取的频率没有取到弹性球壳的共振频点,所以没有观察到相位跳变的现象。再者,材料参数、壳厚对弹性球壳散射声场相位影响很大,实验用的球壳材料参数和壳厚与理论计算存在一定的误差,这也导致实验结果与理论计算结果存在差异。
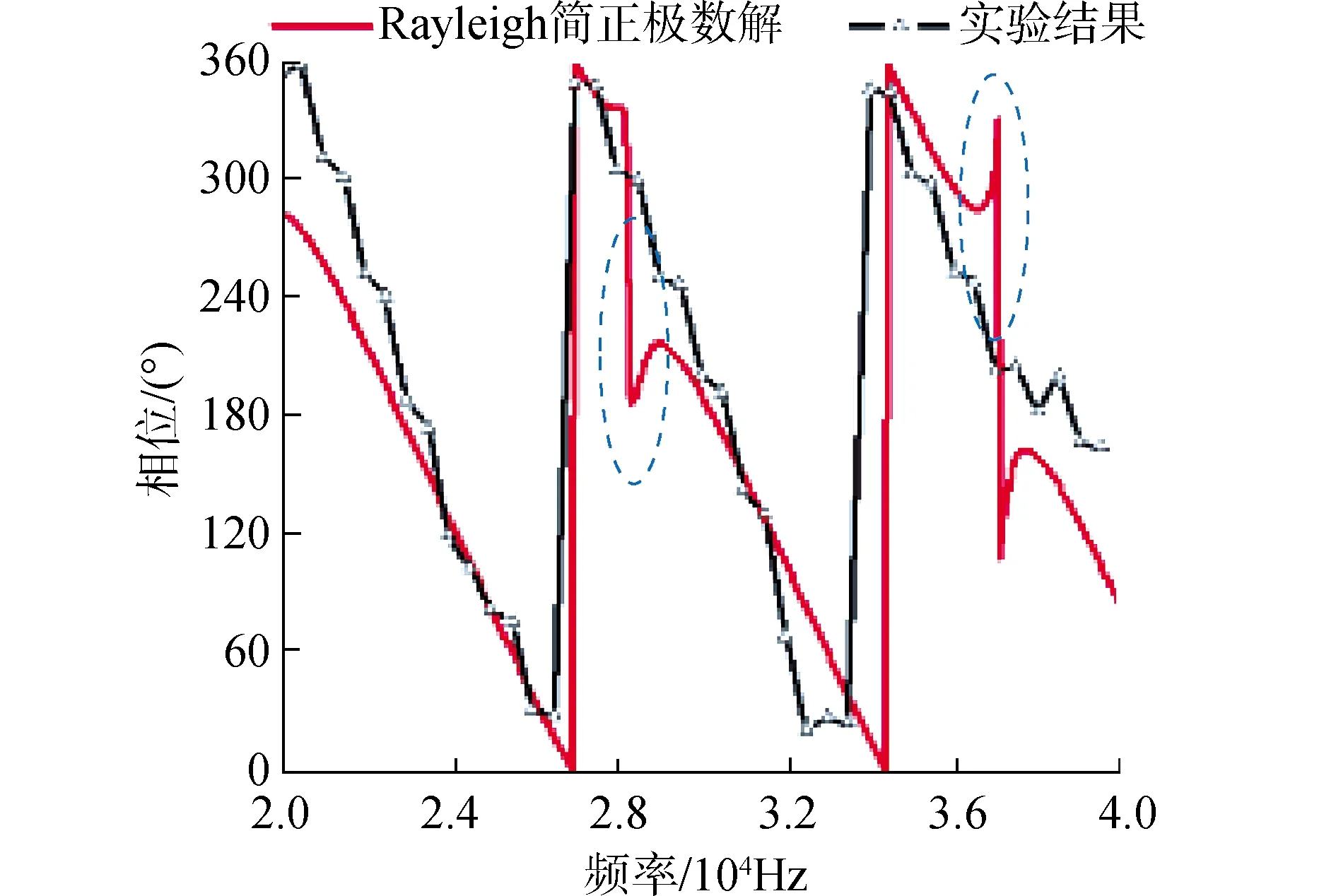
图11 实验结果与Rayleigh简正级数解对比Fig.11 Comparison of theoretical and experimental results
4 结论
1)刚性球在ka>2π时相位随频率呈现接近线性变化。
2)弹性球由于弹性波共振的出现打破了类线性变化规律,特别是在弹性波共振频率处出现相位跳变现象。
3)不同材料、不同壳厚的弹性球壳相频特性有很大的差异,这为利用相位信息进行目标识别提供了可利用特征。
4)通过内部真空弹性球壳的水池声散射实验,利用全相位法获取了其声散射相位特性,与理论预报结果相比吻合较好。
结合有限元方法,突破了解析方法计算任意复杂形状目标声散射的局限性,但高频计算量大,对硬件要求比较高,有限元法较适合于中低频目标的计算,而对于高频水下复杂目标声散射相位计算方法有待探索。另外,对于弹性波共振频率处相位跳变的机理尚未展开深入研究。实验中采用单频点测量,很难取到弹性共振频率点,故实验中没有观察到弹性共振相位跳变的现象。因此,水下目标声散射相位的宽带测量也亟需探究。

