K-Means++的声速剖面精简方法

王振杰， 刘杨范， 赵爽， 王柏杨， 孟庆波

(中国石油大学(华东) 地球科学与技术学院，山东 青岛 266555)

水下声学定位通常采用距离交会方式[1]，水下距离的精确测量受时间测量和声速测量等相关误差影响[2]。借助于高精度的信号检测技术和时延估计方法，在作用距离覆盖范围内测时能够达到优于0.1 ms的精度[3]。声速受深度、温度、盐度等环境因素的综合影响，且存在空变性和时变性[4]。此外，声波在海水中传播产生声线弯曲现象[5]。在高精度水下声学定位中，利用声速剖面(sound velocity profile，SVP)代替固定声速值，并采用分层计算和逐层追加的声线跟踪方法对声线弯曲进行改正[6]。但在深海定位中，SVP的层数较多时，声线跟踪的运算时间显著增加，从而降低了定位效率[7-12]。因此，在保证定位精度的前提下，为了提高水下声学定位计算效率，减少声线跟踪的运算时间，有必要研究实用高效的SVP精简方法。

人工法能够实现SVP的精简，但人工法在精简SVP的过程中易遗漏SVP的特征点，同时效率低下[13]。文献[7]利用Douglas-Peucker算法[14]对原始SVP进行精简，基本解决了声线跟踪精度与计算量之间的矛盾。文献[8]和[9]分别提出了等效声速剖面模型和基于面积差的SVP简化方法，提高了多波束测深效率。文献[10]选用一定宽度的窗口对SVP进行滑动平均，将窗口中声速的平均值作为窗口中心深度的声速值，以此精简SVP，提升了多波束回声测深系统的效率。文献[11]引入等效声速剖面思想，将SVP划为几段，根据等效声速对每段等间隔分层，以提高定位的效率。文献[12]对选定窗口内的声速值进行曲线拟合，计算曲线最大曲率，并以此作为精简SVP的依据，提升了定位效率。以上研究一定程度上精简了原始SVP，提升了多波束测深与水下声学定位的计算效率，但还存在遗漏原始SVP的特征点及在不同深度的定位精度较低等问题。

针对上述问题，本文引入优化聚类算法，提出了一种基于K-Means++[15]的SVP精简方法。该方法采用K-Means++算法实现了对原始SVP的自动精简，有效地解决了定位精度与定位计算效率之间的矛盾。

1 基于K-Means++的SVP精简方法

K-Means算法[16]是聚类算法中的主要算法之一，1967年MacQueen首次提出K-Means算法，该算法的基本原理为：预先确定类别数和初始簇中心将样本集聚为几类，并通过迭代优化获得最终的聚类结果。K-Means算法原理简单，收敛速度快，对大型样本集能高效聚类。但K-Means算法受初始化簇中心的影响较大，当随机初始化簇中心选取不当时，聚类过程非常耗时且聚类结果误差较大。针对这一问题，文献[15]提出了K-Means++算法。K-Means++算法与K-Means算法的原理基本一致，它是对K-Means算法随机初始化簇中心的优化。相较于K-Means算法，K-Means++算法虽然在初始化簇中心时，增加了计算量，但在整个聚类过程中，其显著地提升了计算效率和改善了聚类结果误差。

通过层内常梯度声线跟踪原理[6]得知，每一层有一个常梯度，如果相邻层的常梯度相同，将这2层合并为一层后不会降低层内常梯度声线跟踪的计算精度。根据此原理，本文提出一种基于K-Means++的SVP精简方法，算法流程见图1。

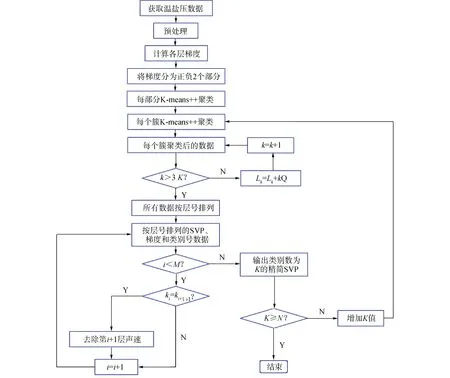
图1 算法流程Fig.1 Algorithm flow chart

2 浮标定位算例分析

为验证基于K-Means++SVP精简方法的有效性，在中国Argo资料中心发布数据中，选取具有代表性[17]的SVP(中国Argo实时资料中心发布温盐压数据，采用W.D.wilson精确声速经验公式[18]计算得到SVP)用于浮标定位，将精简后SVP的定位结果与原始SVP的定位结果进行对比分析。浮标定位中的定位模型为圆曲线模型[19]，声线跟踪方法为层内常梯度声线跟踪方法，解算结果为定位绝对偏差，即应答器解算坐标值与坐标真值的差值。

2.1 浮标定位仿真实验设计

海表面4个浮标的模拟三维坐标分别为B1(-800，-800，0)、B2(-800，800，0)、B3(800，800，0)、B4(800，-800，0)，海底4个应答器的模拟三维坐标分别为T1(0，0，-1 000)、T2(0，50，-1 000)、T3(50，0，-1 000)、T4(50，50，-1 000)，单位均为m，模拟历元为100个历元，原始SVP的深度范围为0～1 000 m，采样间隔为1 m。海面余弦波动振幅为2 m，应答器时延偏差为8 cm，测量时间引起的测距中误差为10 cm。浮标和应答器的相对位置示意图如图2所示，浮标B2坐标放大图如图3。实验中计算平台的处理器型号为Intel(R) Core(TM) i5-6500，内存大小为8 G。

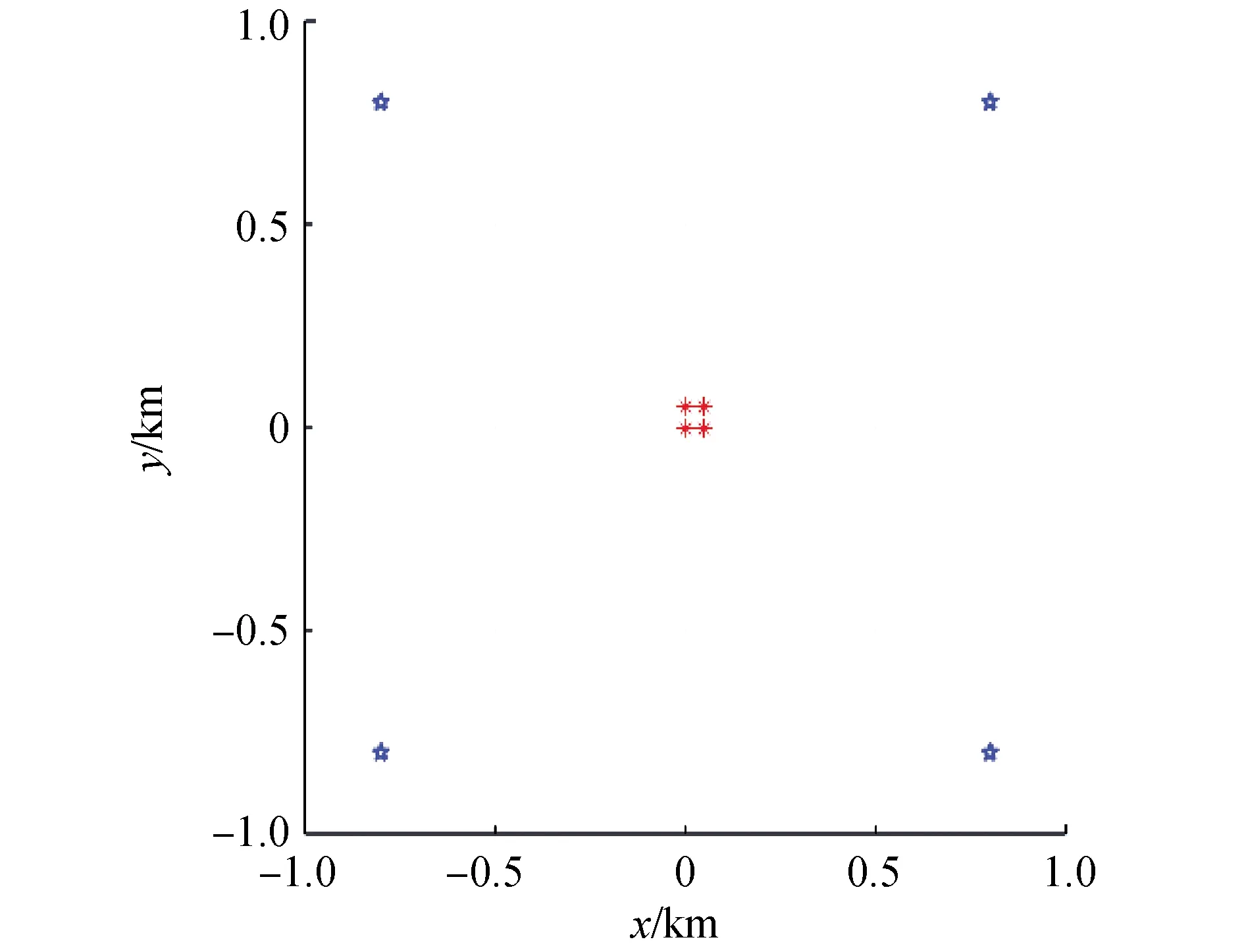
图2 浮标和应答器模拟坐标示意Fig.2 Schematic diagram of buoy and transponder simulation coordinates

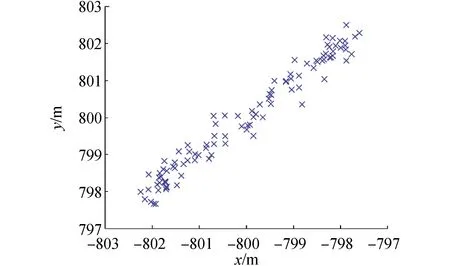
图3 浮标B2 100个历元坐标示意Fig.3 Schematic diagram of buoy B2 100 epoch coordinates

2.2 不同类别数精简SVP与原始SVP对比

为检验精简后SVP是否保留了原始SVP的特征点，选取类别数2～10精简SVP，并将精简后的SVP与原始SVP对比分析，如图4和表1所示。图4对类别数2、4、5和10的精简结果进行展示，其余不再赘述。表1中的类别数1表示原始SVP。

表1 不同类别数的SVP精简结果Table 1 SVP streamlined results for different categories

特征率指精简后SVP所包含原始SVP的特征信息，其计算公式为：

(1)

式中：i表示类别数；Pi表示类别数为i精简后SVP层数；P表示原始SVP层数。

由图4和表1可知，类别数较小时，特征率较低，精简后的SVP与原始SVP差异较大。随着类别数增加，特征率不断提高，精简后的SVP逐渐与原始SVP重合。当类别数增加到5时，特征率为11.9%，精简后的SVP与原始SVP基本完全重合。表明本实验中特征率大于等于11.9%时，精简后的SVP基本保留了原始SVP所有特征，确保了原始SVP的空间结构。

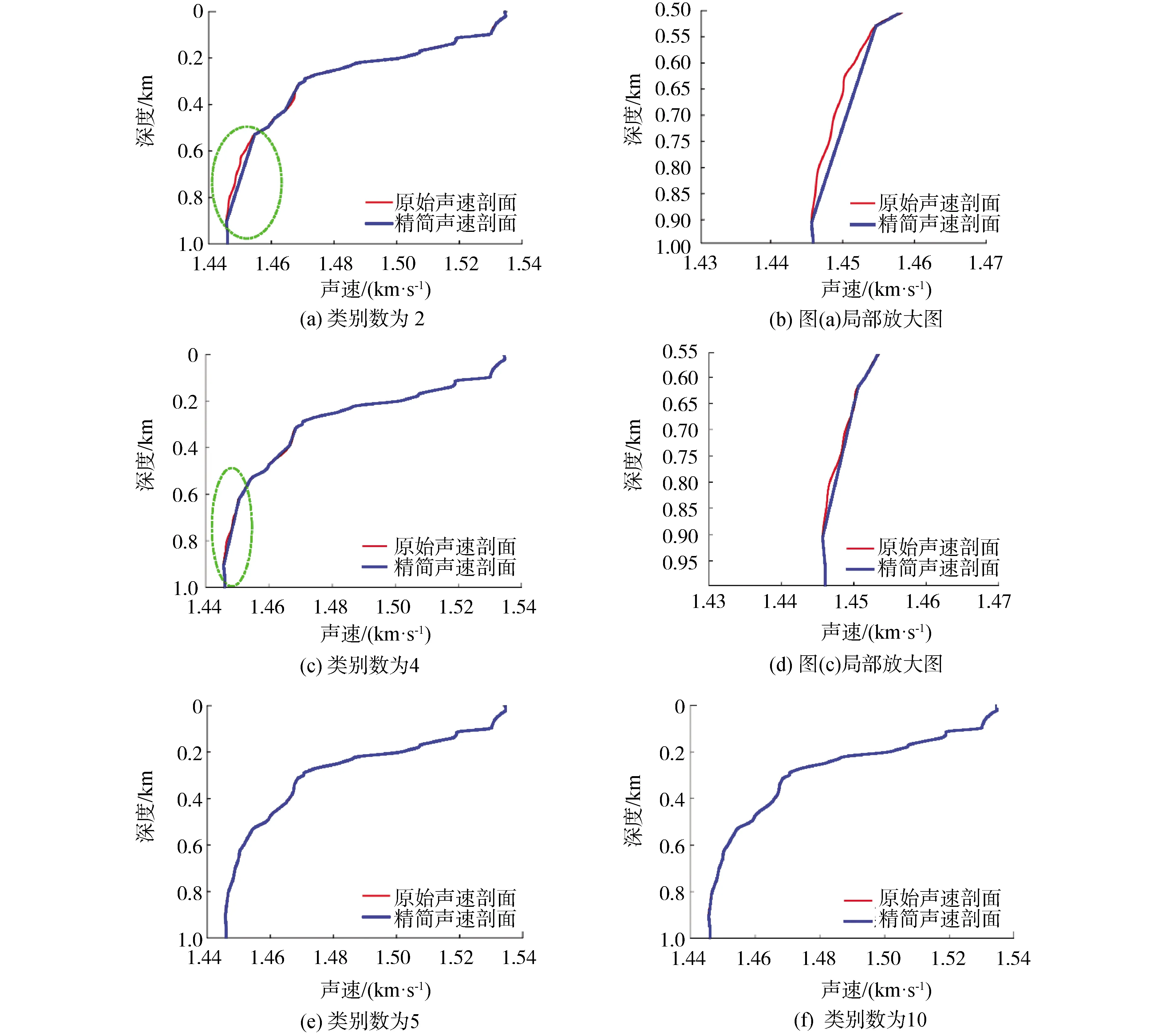
图4 不同类别数精简SVP与原始SVP对比Fig.4 Comparison of different categories of streamlined SVP and original SVP

2.3 不同类别数定位结果分析

为比较精简后SVP与原始SVP的定位结果，从定位效率和定位精度2个方面进行分析，如图5、表2和图6所示。类别数为1表示原始SVP的定位结果。

定位效率方面：由图5可知，类别数从2到10，精简后SVP的层数从55层到208层，远小于原始SVP的1 000层，精简后SVP的定位时间从2.1 s到6.6 s，也远小于原始SVP的40.4 s，定位时间缩短了83.6%～94.9%，定位效率较原始SVP大幅度提升。

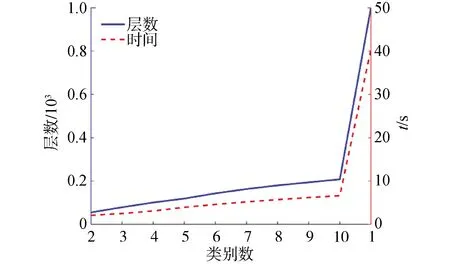
图5 不同类别数精简SVP的层数和定位时间Fig.5 Layers and positioning time of streamlined SVP for different categories

定位精度方面：由表2可知，类别数从2到4，精简后SVP的水平最大误差从0.058 7 m降低到0.038 5 m，垂直最大误差从0.757 2 m降低到0.160 4 m，垂直最小误差从0.744 3 m降低到0.147 5 m，水平平均误差从0.020 2 m降低到0.010 1 m，垂直平均误差从0.748 3 m降低到0.151 5 m。类别数从4到5，精简后SVP的垂直最大误差从0.160 4 m减小到0.122 1 m，垂直最小误差从0.147 5 m减小到0.108 2 m，垂直平均误差从0.151 5 m减小到0.113 2 m。类别数从5到10，精简后SVP的各个误差基本保持不变，并与原始SVP的定位误差基本一致。

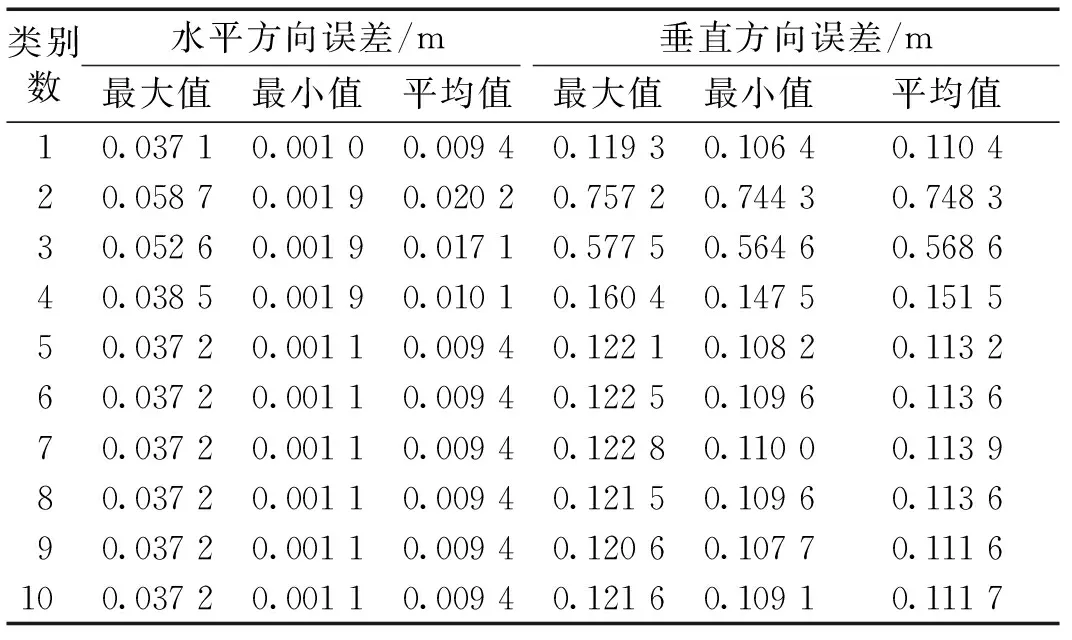
表2 不同类别数的应答器定位误差Table 2 Transponder positioning error of different categories

上述实验表明，随着类别数增加，定位误差逐渐减小，当类别数大于等于5时，精简后SVP的定位精度与原始SVP区别不大，差别为毫米级，而定位计算效率显著高于原始SVP。

2.4 不同深度定位精度分析

采用精简后的SVP进行水下定位时，虽然保证了原始SVP采样深度处的定位精度，但可能会使该水域其他深度处的定位精度产生较大误差[9]。

为验证采用本文方法精简的SVP在其他深度处的定位精度，对精简后SVP的不同深度定位结果进行分析，并与原始SVP进行比较，如图6所示。由上述实验可知，当类别数大于等于5时，精简后SVP的定位精度与原始SVP基本相同，所以本实验的类别数为5～10。本实验中浮标布设间距为1 600 m，考虑声线入射角,设置深度区间为400～900 m。本文原始SVP测量处的深度为1 000 m。

图6 不同深度定位结果RMSFig.6 RMS of positioning results for different depths

由图6(a)可知，深度为400 m，精简后SVP定位结果的水平方向RMS(root mean square)为0.009 6～0.009 7 m，原始SVP为0.009 7 m；深度为600 m，精简后SVP定位结果的水平方向RMS为0.011 4～0.011 5 m，原始SVP为0.011 4 m；深度为900 m，精简后SVP定位结果的水平方向RMS为0.012 4～0.012 5 m，原始SVP为0.012 4 m。由图6(b)可知，深度为400 m，精简后SVP定位结果的垂直方向RMS为0.188 7～0.197 1 m，原始SVP为0.198 7 m；深度为600 m，精简后SVP定位结果的垂直方向RMS为0.133 9～0.148 5 m，原始SVP为0.149 9 m；深度为900 m，精简后SVP定位结果的垂直方向RMS为0.120 8～0.123 2 m，原始SVP为0.118 9 m。再由图6可知，同一深度不同类别数所对应的颜色基本相同，表明同一深度精简后SVP的RMS与原始SVP基本相同(水平方向RMS基本一致，垂直方向RMS差别为0～0.018 2 m)。通过实验数据分析可知，本文方法在不同深度进行水下定位时，精简后SVP各个深度处的定位精度与原始SVP相应深度处的定位精度基本一致。

3 结论

1)本文提出的一种基于K-Means++的SVP精简方法采用不同类别数对原始SVP进行精简，当类别数大于等于5时(5表示本算例的类别数阈值)，精简后SVP基本保留了原始SVP的所有特征。

2)精简后SVP的定位精度与原始SVP基本相同，而定位效率明显高于原始SVP；在不同深度进行水下定位，精简后SVP的定位精度与原始SVP基本一致。

3)由于不同SVP受区域、时间、采样等因素影响，因此其他算例中的类别数阈值可能会与本算例略有不同，但本文所提方法和所得规律性结论均具有普适性。

4)本文方法实现了原始SVP的自动精简，精简后的SVP在确保原始SVP空间结构和水下定位精度的前提下，缩短了声线跟踪的运算时间，进而显著提高了水下定位计算效率，具有良好的工程应用价值。