循环流化床制冰系统用喷嘴的数值模拟研究

王 鑫，孙 靖，韩克鑫，谢春刚，邢玉雷

(1. 自然资源部天津海水淡化与综合利用研究所，天津 300192；2. 天津市海跃水处理高科技有限公司，天津 300192)

冷冻海水淡化是海水在低温下冷却至结冰，冰晶经分离、洗涤、融化后得到淡水的技术[1]。其具有工艺能耗低，海水低温下腐蚀、结垢倾向低，设备投资成本低，无需海水预处理及药剂等诸多优势，是一项具有发展潜力的海水淡化技术。流化床制冰用于冷冻海水淡化是一种新型的冷冻淡化方法，该方法是海水通过传热管与载冷剂逆流换热生成冰晶，冰晶粘附于传热管壁面，海水中流态化固体颗粒与壁面碰撞去除壁面冰晶形成冰浆。由于颗粒运动造成大量湍流，使得流化床制冰器具备更高的传热效率，且颗粒运动类似流体，可实现不同换热管间热质的传递，易于规模扩展，能满足工业化大批量连续作业的需求。关于流化床制冰技术，国内外学者已经开展了一些实验研究。E.Stamatiou等[2]详细分析阐述了流化床制冰器的基本工作原理、操作范围和传热特性。P.Pronk等[3]采用流化床技术对质量浓度为7.7%氯化钠溶液进行制冰性能的研究，测试了系统稳定运行的边界条件，同时通过对比试验发现循环流化床具备更宽的参数调节范围。J.W.Meewisse等[4]开展了流化床制冰性能测试，并建立了传热系数计算模型。然而该技术用于海水制冰淡化尚未见报道。

循环流化床是介于传统非循环流化床和稀相输送床之间的一种操作形式，因其具备操作范围广、表观流速高、床内颗粒分布较均匀及易于操作等优点，现已广泛应用于化工、机械、水处理等诸多领域[5-7]。刘燕等[8]模拟研究了循环流化床喷嘴对流场的影响。P.Pronk等[3]研究了循环流化床制冰系统中颗粒上升速度对制冰传热温差(除冰速率)的影响。研究发现随着颗粒循环流速的增加颗粒去除冰晶的速度会提高。因此，提高颗粒循环速度对循环流化床制冰效率意义重大。为提高循环流化床循环动力，在下降管与水平进水管三通处加入喷嘴，喷嘴出口位置Nozzle Exit Position (NXP)及口径比Diameter Ratio (DR)对颗粒循环速率影响很大，通过设计合理的NXP及DR，可以在降低喷嘴本身压降的同时，使其对下降管内水流的卷吸作用最大。文章为进一步掌握提高颗粒循环速度的方法，对加入喷嘴的循环流化床内部流场进行模拟，求得循环流化床制冰系统中喷嘴的最优设计方案。

1 流化床制冰系统

如图1所示，载冷剂吸收冷量进入流化床制冰器的壳程与传热管内的海水逆流换热，升温后的载冷剂返回换热器继续降温循环使用。在制冰器内，固体颗粒在海水的带动下实现流态化，颗粒通过碰撞传热管壁将粘附在壁面的冰晶除去形成冰晶、浓海水与颗粒组成的混合体系。混合流体进入悬液分离器，冰晶与浓海水从顶部排出，颗粒及少量浓海水从底部下降管回流至海水入口管。顶部排出的冰晶与浓海水进入水箱，冰晶被滤网拦截，浓海水与进料海水混合以保证系统盐度平衡，并通过水泵和喷嘴与下降管内颗粒及少量浓海水混合后一同进入制冰器制冰。

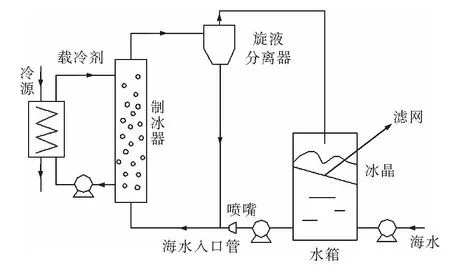
图1 实验系统示意图Fig.1 Schematic diagram of experimental system

喷嘴是影响颗粒循环性能的关键部件，喷嘴出口压力变化对下降段内流体卷吸力有重要的影响[9]。由于受到实验测量手段和水平管直径较小的限制，喷嘴出口压力测量探管对管内流场有较大的干扰作用，导致测量数据不够精确。为弥补实验测量手段的不足，文章采用计算流体力学的数值模拟计算方法研究喷嘴附近区域的流场变化规律。

2 CFD模拟

2.1 几何模型

文章计算域的几何模型与网格如图2所示。采用Gambit对计算域进行网格划分，网格类型全部采用四边形，并对壁面处流动边界层网格进行加密，计算域网格数量为637 528。如图3所示，喷嘴口径比DR=d/D，喷嘴出口位置NXP=L，定义下降段左侧边缘作为安装零点，-40 mm、-20 mm、0 mm、20 mm的位置见图3，并规定零点右侧为x轴正方向，左侧为负方向。

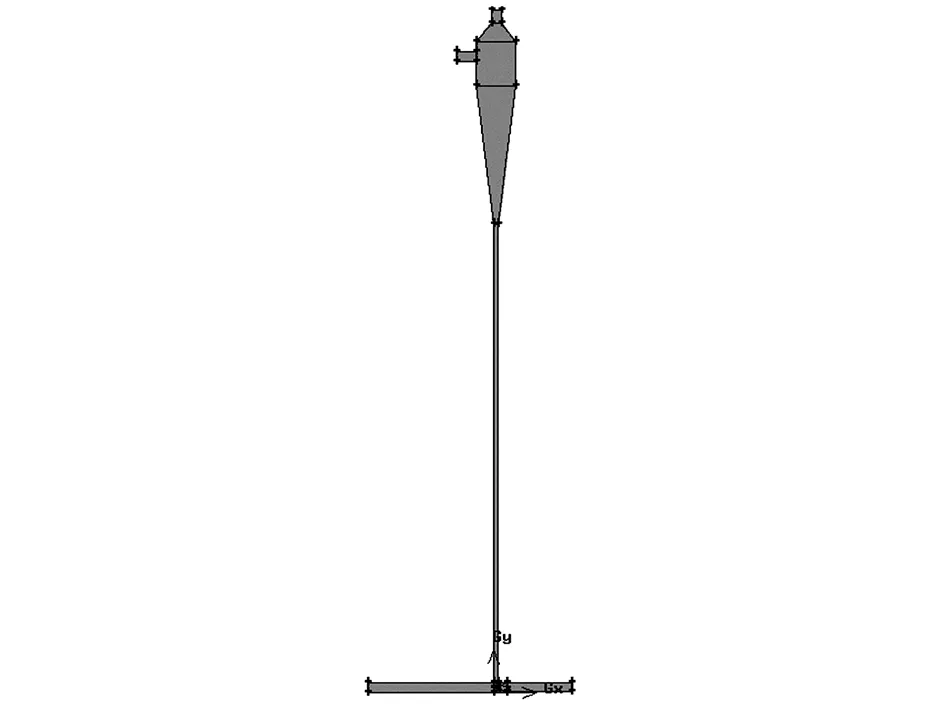
图2 几何模型与网格示意图Fig.2 Geometric model and mesh diagram

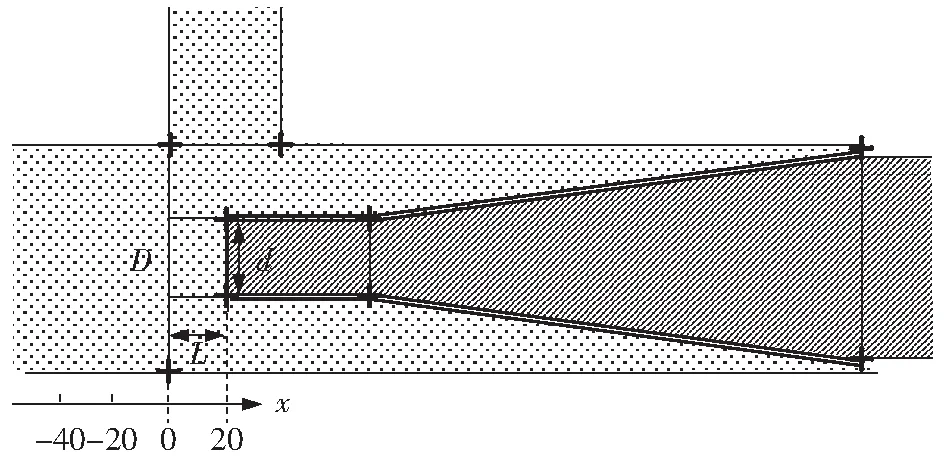
图3 喷嘴口径比与出口位置示意图Fig.3 Schematic diagram of nazzle diameter ratio and outlet position

2.2 控制方程

计算流体力学的基本控制方程包含：质量守恒方程、动量守恒方程等[10]。这些方程是所有流体流动都要遵守的基本物理定律的数学表达形式。

(1)质量守恒方程

质量守恒方程又叫连续性方程，其一般形式如下：

(1)

(2)动量守恒方程

动量守恒方程又叫Navier-Stokes方程(粘性流体)，在惯性坐标系下，其一般形式如下：

(2)

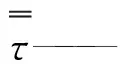
(3)

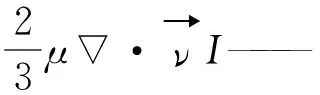
(3)湍流模型

由于水平管内部流动为湍流流动，需进行流体湍流行为的模拟。FLUENT中提供的标准k-ε湍流方程是最常见的双方程湍流模型，作为工程流场计算中主要的工具，应用十分广泛。

湍动能k方程：

(4)

湍流耗散率ε方程：

(5)

式中:μl——层流粘性系数；μt——湍流粘性系数，且μt=ρCμk2/ε；Gk——由平均速度梯度引起的湍动能；Gb——由浮力影响产生的湍流动能。有效粘度系数μ=μl+μt；模型常数取值为：Cμ=0.09，C1ε=1.44，C2ε=1.92，C3ε=0.99，σk=1.0，σε=1.3。

2.3 边界条件

模拟计算中，水平管的入口及旋液分离器切向进口均设置为速度入口(Velocity inlet)，速度入口的速度数值根据实验数据设定；假设水平管足够长，忽略喷嘴对其流场的影响，水平管出口设置为压力出口(Pressure outlet)；对于旋液分离器溢流水进入储水箱，所以对溢流管出口也设置为压力出口(Pressure outlet)。具体边界条件设置见表1。模拟的流体介质选择为纯水，重力加速度方向垂直向下。

表1 边界条件参数Tab.1 Boundary condition parameters

2.4 模拟算法

文章采用商用计算流体力学软件ANSYS FLUENT进行模拟计算，采用有限体积法对计算求解区域进行求解计算。压力和速度耦合采用SIMPLE算法，湍流模型采用标准k-ε双方程湍流模型，壁面区域采用标准壁面函数法，各计算变量的残差值设置为10-4。

3 结果与分析

文章分别模拟研究了4个喷嘴出口位置NXP=-40 mm、-20 mm、0 mm、20 mm，3个口径比DR=0.2、0.3、0.4。重点分析了不同几何设置条件下，水平管中心轴线上(如图4)的流场、压降、湍动能以及旋涡等物理量的变化规律。

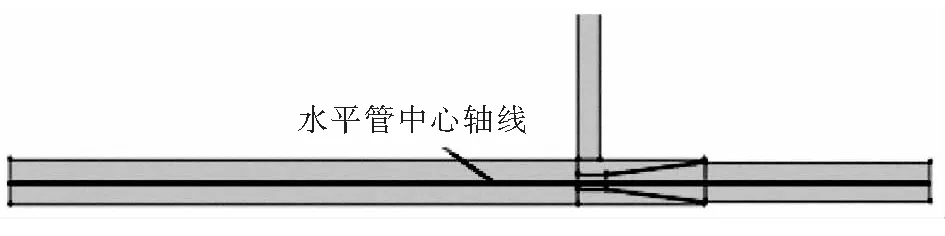
图4 水平管中心轴线位置示意图Fig.4 Schematic diagram of horizontal pipe central axis location

3.1 NXP对流场的影响

选择喷嘴直径为24 mm，即DR=0.3时，进行NXP对管内流场影响的研究。分别研究了NXP=-40 mm、-20 mm、0 mm、20 mm时，其对于管内流体的速度、湍动能、漩涡等分布的影响。为便于研究，考虑到水平管中心轴线位置流体存在较大的速度梯度，故将水平管中心轴线作为模拟计算监测位置，并规定喷嘴出口处为坐标原点，流体来流方向为正，出流方向为负，相应的模拟结果与分析讨论如下。

3.1.1 NXP对速度的影响

图5所示的是不同NXP水平管中心轴线位置(-0.125 m≤x≤0.125 m)的速度分布。

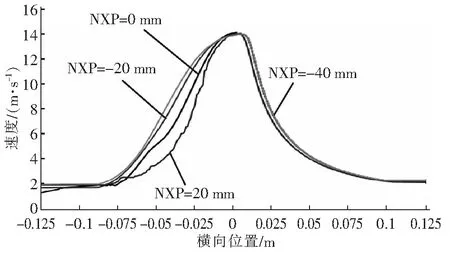
图5 不同NXP水平管中心轴线位置速度分布Fig.5 Velocity distribution of different NXP horizontal pipe central axis position

从图5中可以看出，对于相同的NXP，喷嘴均对来流的流体起到了加速作用。在x=0 m时，即喷嘴出口位置，流体的速度达到最大值。当流体流出喷嘴后，由于水平管道直径较小，流体流动需克服管道边界的摩擦阻力变大，需要消耗更多的流体动能来克服摩擦粘滞阻力，因此流体的流速逐渐变小，直至与来流的速度相当。通过在相同轴线位置比较不同NXP的速度值，当NXP=0 mm时，流体在流出喷嘴出口以后速度减小的趋势最慢，但是当x=-0.1 m时，不同NXP下的速度值基本一致。由于流速在流出喷嘴出口后0.05 m范围内存在明显的变化规律，此处取x=-0.05 m时不同NXP的速度值，将该速度值与相应最大速度值进行相对变化大小的比较。当NXP=20 mm时，速度变化相对大小为63%，当NXP=0 mm时，速度变化相对大小为33%，相差30%。由于速度变化越缓慢，代表喷嘴对流体的射流作用越大，故当NXP=0 mm时，喷嘴射流影响距离最远。

3.1.2 NXP对湍动能的影响

图6所示的是不同NXP对流体湍动能的影响变化曲线图。从图6可以看出，流体流入喷嘴直至喷嘴出口，湍动能变化缓慢。当流体从喷嘴喷出后，流体的湍动能开始快速地增大，并在x=-0.07 m附近，湍动能达到最大值，随后又逐渐变小。出现图6中湍动能变化趋势的原因在于：当流体从来流方向直至进入喷嘴，喷嘴中心流体射流速度脉动幅度较小，故出现了图中当x>0 m时的湍动能变化幅度很小的情况。当流体从喷嘴喷出后，由于流体速度出现一定程度的剧烈脉动，故存在一定距离范围内湍动能的急剧增加。但是，随着流动距离的增长，受水平管内壁面与喷嘴喷射范围的影响，以及湍流剪切力的作用，湍动能迅速减小。当流体的动能消耗致使流体的动力不足时，水平管内的流动最终变为层流流动，即湍动能减小到一个稳定的平衡值。当NXP=0 mm和20 mm时，由于竖管下降段的来流流体对喷嘴出口的射流流体有直接的干扰，使得NXP=0 mm和20 mm的湍动能在离开喷嘴处最先开始变化。

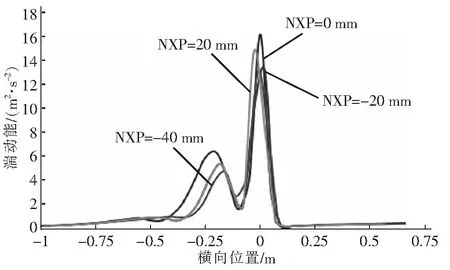
图6 不同NXP对流体湍动能的影响Fig.6 Effect of different NXP on turbulent kinetic energy of fluid

3.1.3 NXP对漩涡的影响

图7是不同NXP下水平管内部流体的速度矢量图。

当NXP=0 mm时，流体从喷嘴出口喷出后，由于受到较大射流速度的影响，在喷嘴出口区域形成以中心射流区域为中心线的上下两个漩涡。下漩涡的流量主要来自于水平管段来流的流体，上漩涡的来流主要来源于喷嘴对于竖直管段流体的卷吸。下漩涡比上漩涡影响区域大，说明由于喷嘴的存在其对下降管段内的流体有较强的卷吸作用。当NXP=20 mm时，由于喷嘴出口的位置处于下降管段出口的正下方，下降管段流体由于受到重力作用，对喷嘴出口喷出的流体形成了较强的下压作用，导致喷嘴出口喷出的流体迅速下降，并沿着水平管底部壁面流动。

从图7中的速度矢量可以看出，当NXP=20 mm时，喷嘴喷出流体的上部没有明显漩涡存在，说明喷嘴对于下降管流体的卷吸作用很弱，漩涡的大小较小，漩涡的影响距离较小。当NXP=-20 mm和NXP=-40 mm时，由于喷嘴出口位置均处于水平管段的下游，喷嘴喷出流体的上部虽然也有一定程度的漩涡存在，但此处漩涡的强度较小，对于下降管的卷吸作用较弱。综合比较NXP=0 mm时，上漩涡的影响范围最大，有利于喷嘴对于竖直管段流体的卷吸。

3.2 DR对流场的影响

选择喷嘴出口位置NXP = 0 mm时，进行DR对管内流场影响的研究。分别研究了DR=0.2、0.3、0.4时，其对于管内流体的速度、漩涡、压降等分布的影响。

3.2.1 DR对漩涡的影响

图8是不同DR下的流场分布图。从图8可以看出，当DR=0.2时，漩涡影响的面积最大；当DR=0.4时，漩涡影响的面积最小，但是上下漩涡较为对称，且流速大小适中。

3.2.2 DR对压降的影响

图9所示的是DR=0.2、0.3、0.4时的压降变化分布曲线图。从图9中可以看出，在流体进入喷嘴前，在DR=0.2时的压力最大，在DR=0.4时的压力最小。DR越小，喷嘴出口的压力值越低。造成这种现象的主要原因是：当DR越小时，喷嘴对于流体流动的阻力越大，流体经过喷嘴加速喷出后所形成的负压越大。从图9还可以看出，当DR=0.3时，即喷嘴喉部直径为24 mm时，压降变化幅度变小，喷嘴阻力较小，更有利于流体的流动循环。

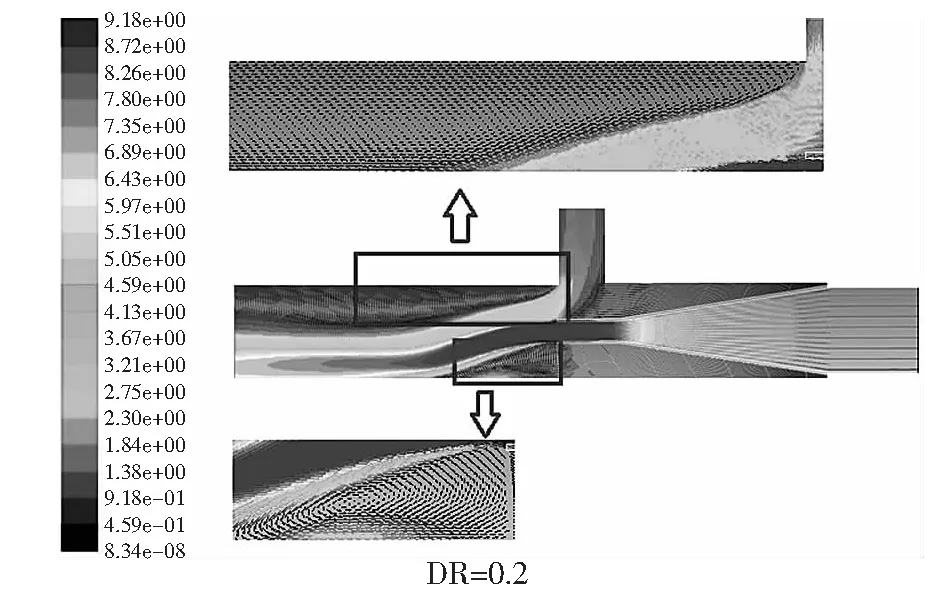
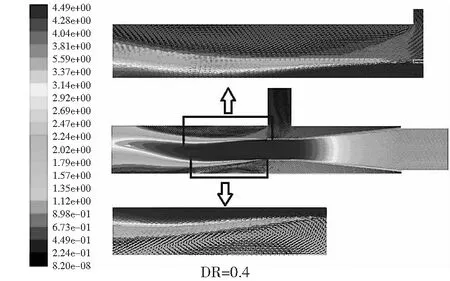
图8 不同DR下的流场分布图Fig.8 Flow field distribution under different DR

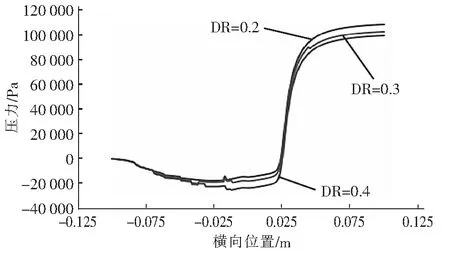
图9 不同DR的压降变化分布曲线Fig.9 Pressure drop distribution curve of different DR

4 结论

文章通过采用计算流体力学方法，以循环流化床制冰系统中的喷嘴为研究对象，针对喷嘴不同NXP、DR进行模拟研究，得出如下主要结论：

1)NXP是影响喷嘴喷射距离和卷吸竖管流体的关键因素。在喷嘴出口区域形成以中心射流区域为中心线的上下两个漩涡，上漩涡对竖管中的流体有卷吸作用。当NXP=0 mm，流体速度变化率较慢，喷嘴出口射流中心区域较长，射流区域产生的漩涡影响距离长，有利于流体的循环。

2)DR是影响流体漩涡面积和压降的关键因素。当DR=0.3时，漩涡影响的面积较大。同时，压降变化幅度较小，喷嘴前后的阻力较小，更有利于流体的流动循环。