落物冲击下煤矿胶轮车驾驶室上部结构优化

宋 涛，张 凡

1中国煤炭科工集团太原研究院有限公司 山西太原 030006

2煤炭科学研究总院 北京 100000

煤矿防爆无轨胶轮车作为我国煤矿井下主要运输方式之一[1-2]，其长期在恶劣环境中作业，时常发生的煤岩、混凝土块等落物坠落和崩塌事故威胁车辆乘员人身安全。为应对这种情况，国际上通常是强制在工程车辆驾驶室上安装落物保护结构 (Falling Object Protective Structures，FOPS)，以达到保护驾驶人员的目的，并制定了安全法规对 FOPS的试验方法进行了要求[3]。

随着国内对于工程机械驾驶室安全性能要求的提高，国内许多高校与企业对 FOPS结构展开了研究。吉林大学冯素丽博士[4]与聂兆霖[5]对自卸车落物保护结构的安全性能进行了计算机仿真，并进行了试验验证。湘潭大学的欧阳文一[6]总结了落物保护结构的性能要求与试验方法，并以某型挖掘机为例进行了有限元分析与试验研究。天津大学的刘志鹏[7]基于弹塑性力学理论对装载机落物保护结构进行了动态与静态有限元分析。上述研究主要是针对地面工程车辆，对于煤矿井下胶轮车驾驶室结构的安全性能研究极少。

笔者对 WC8E型煤矿胶轮车驾驶室进行了落物冲击试验，根据试验结果提取出驾驶室上部结构，并采用拓扑优化与融合算法相结合的优化方法对上部结构进行了优化设计，为胶轮车驾驶室的设计提供了参考。

1 落物撞击试验

1.1 驾驶室显式动力学模型建立

以 WC8E型胶轮车为例，建立其驾驶室有限元模型 (见图 1)，为了提高计算效率，去除门窗、塑封胶条、仪表盘以及细微倒角和开孔等对驾驶室强度影响较小的结构，其中 DLV (挠曲极限量) 为穿普通衣服、戴安全帽、坐姿高大男性司机的垂直投影值，如图 1(a) 所示。经测量，司机头部与驾驶室顶部结构最小距离为 120 mm。

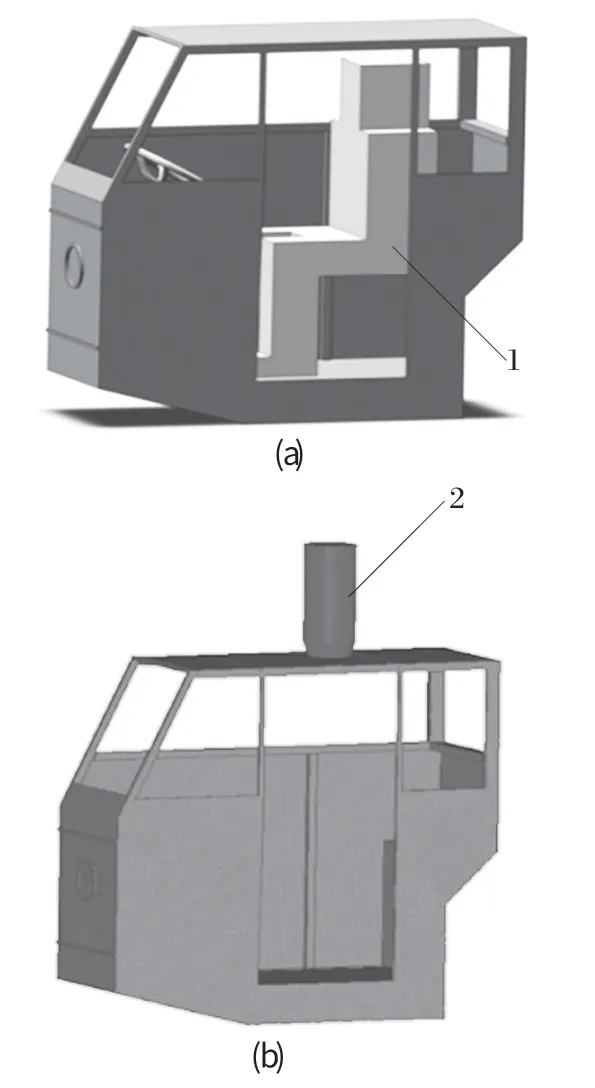
图1 WC8E胶轮车驾驶室有限元模型Fig.1 Finite element model of cab of WC8E rubber-wheeled vehicle

根据标准 ISO3449验收基准Ⅱ的规定，驾驶室上部结构需承受标准直径不大于 400 mm的落锤产生的11 600 J冲击能量而不被穿透，同时驾驶室上部机构不允许侵入 DLV空间。因此选取直径为 260 mm、质量为 227 kg标准落锤，如图 1(b) 所示。以 10.11 m/s的速度对驾驶室顶部结构进行冲击试验，其撞击位置处于 DLV头部垂直投影区域内，以模拟最恶劣落物冲击工况。冲击能量

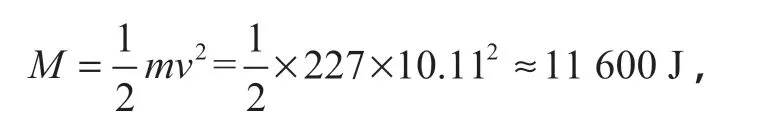
满足标准要求。

1.2 原始结构落物冲击分析

根据建立的动力学有限元模型，提交 LS-DYNA求解器进行求解，将结果进行输出，得到驾驶室最大变形如图 2所示。从图 2可以看出，驾驶室顶部结构最大变形量为 103 mm，变形主要集中于顶部内侧横梁与外侧两根立柱上；而在撞击点附近出现了应力集中现象，前后立柱变形极小，表明顶部加强梁框架并不能很好地分散冲击力，当落物撞击点位于驾驶人员头部上方处时，极易造成人员损伤。

从变形上看，驾驶室顶部结构水平传力路径不合理，导致驾驶室垂直方向变形过大，侵入驾驶员安全生存空间，因此有必要提取驾驶室上部结构对其进行优化设计。驾驶室上部结构如图 2(b) 所示。

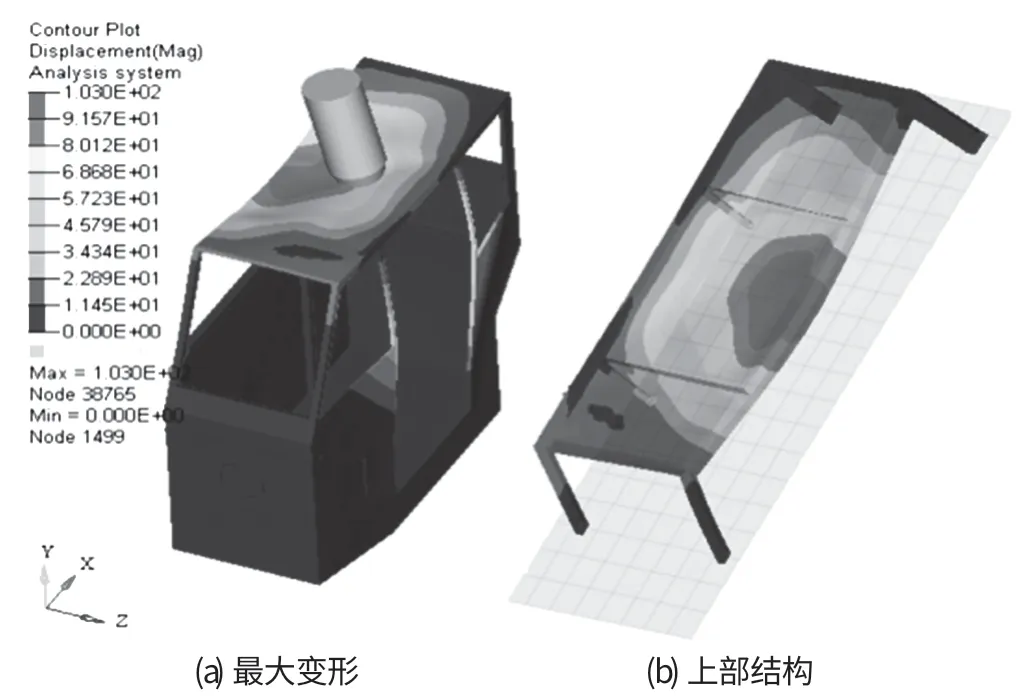
图2 驾驶室的最大变形与上部结构Fig.2 Maximum deformation and upper structure of cab

2 拓扑优化数学模型

根据落锤撞击试验结果，分解胶轮车驾驶室上部结构进行拓扑优化，以冲击力峰值为载荷条件，采用各向正交惩罚材料密度法 (SIMP)，即将模型中“单元密度”作为设计变量，在 0～ 1之间取连续值，优化求解后单元密度越靠近 1，则表明该位置的材料较为重要，需要保留。

优化数学模型为

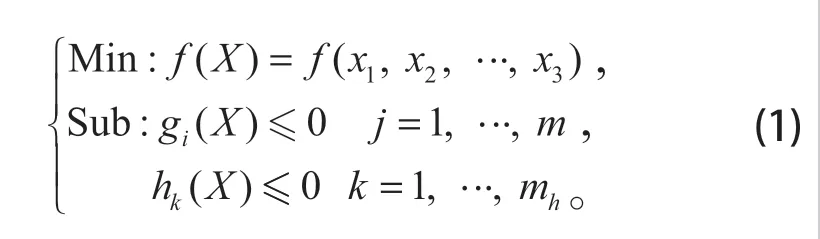
式中：X为设计变量，指的是设计区域内单元密度；f(X) 为设计目标，指的是驾驶室结构质量最小化；g(X)和h(X) 为约束条件，分别代表上部结构最大变形为75 mm和优化体积上限为 30%。

将质量最小化模型等效为体积分数最小化，则目标函数为

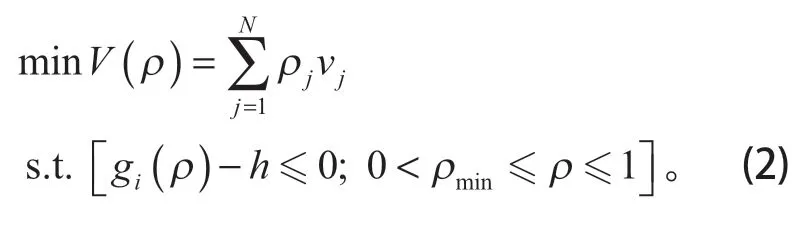
设计灵敏度指的是响应对于优化变量的偏导数，其大小反应了设计变量对目标函数变化影响的程度，对式 (3) 进行求偏导，得到体积分数灵敏度方程为

3 拓扑优化设计

将上述数学模型代入 optistruct软件进行优化求解，当迭代次数到达 28次时，收敛结果，得到拓扑优化后密度云图，如图 3所示。

图3 拓扑优化后的密度云图与工程解读Fig.3 Density contours and engineering illustration after topological optimization

从图 3密度云图可以看出，深色部分单元密度趋于 1，代表需要加强；从工程解读中可以看出，当驾驶室顶部受落物冲击后，力沿着撞击点主要分为 6个路径进行扩散，其中路径 2与路径 3传力比例最大，立柱 2、3、5和 6为主要垂向载荷承载立柱，而立柱1和 4承载较小，强度有所冗余。

因此除了对加强梁布置结构重新规划外，考虑到轻量化因素，需对 2、3、5、6号立柱和上下横梁所用矩形钢管从 3 mm壁厚增加为 4 mm厚，1和 4号立柱壁厚从 3 mm降至 2 mm厚；考虑到尖锐岩块落物对驾驶室有穿透风险，因此保持顶部结构钢板厚度 3 mm不变。根据密度云图与传力路径，对顶部结构加强梁布置进行重新设计，布置方案为 A和 a，如图 4所示，加强梁壁厚初步选定 B (3 mm) 和 b (2 mm)。

图4 加强梁布置方案Fig.4 Layout scheme of reinforcement beam

将 4种优化方案参数输入驾驶室上部结构中进行重新建模，对其进行落物冲击仿真，并将结果输出进行综合对比，结果如表 1所列。

表1 优化方案结果对比Tab.1 Comparison of optimization scheme in results

设计目标是控制驾驶室顶部结构变形量不超过75 mm，同时质量最轻，可以看出在 2种厚度下，加强梁布置方案 a性能均优于方案 A，故选取方案 a为最终布置方案。

4 粒子群与人工鱼群融合算法优化

4.1 驾驶室上部结构理论模型

上部结构加强梁布置选取方案 a，加强梁采用空心矩形梁，如图 5所示。

则驾驶室上部结构质量为

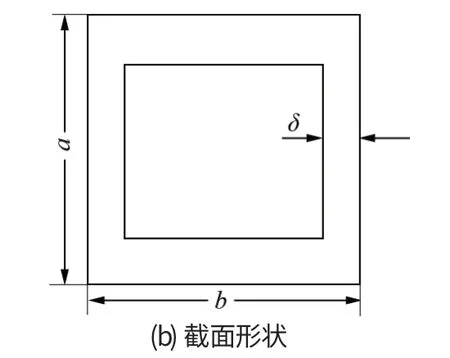
图5 加强梁布置方案与截面形状Fig.5 Layout scheme and cross-section shape of reinforcement beam

对加强梁结构局部稳定性进行分析，当弯曲应力、切应力和局部挤压应力作用时的临界应力分别为

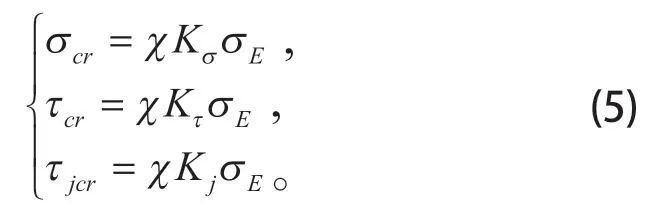
式中：χ为板边嵌固系数；K为局部稳定系数。

临界复合应力可以表示为

式中：γ为截面两边缘弯曲应力弯曲应力比，值为 1。

4.2 融合算法原理

粒子群算法 (PSO)[8-9]又被称为鸟群捕食算法，该算法中每只鸟的位置代表了一个粒子，每个粒子还有一个速度决定它们飞翔的方向和速率，然后，粒子们就追随当前的最优粒子在解空间中搜索。其中迭代中每个粒子的速度和位置通过式 (7) 进行更新。

式中：vni(t) 为粒子n的i维的第t代；c为学习因子；r为 [0，1] 之间的随机数字；pg为全局最优位置。

人工鱼群算法是通过模拟鱼群个体之间通过合作来完成觅食的过程，对每条人工与个体进行评价，对觅食 Pray、聚群 Swarm、追尾 Follow和评价行为bulletin进行选择，来达到寻求全局最优解的过程[10]。

人工鱼群算法在全局寻优过程中，对复杂目标算法的收敛速度会降低[6]，而粒子群算法恰恰能弥补这一点，因此将这 2种算法进行融合使用。具体思路为：每执行完一次粒子群算法迭代之后，进行一次人工鱼群算法迭代，当粒子群迭代所得函数值小于人工鱼群公告板上函数值，则更新本次算法中最优个体位置，否则保持不变，按此方法进行迭代计算，直至收敛或者完成所需迭代次数，如图 6所示。

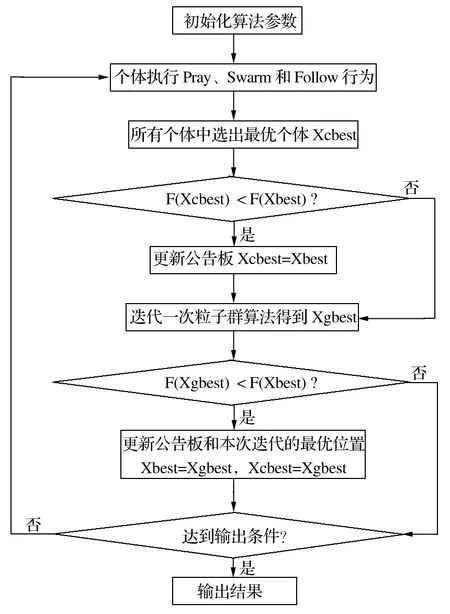
图6 融合算法优化流程Fig.6 Process flow of fusing algorithm

4.3 优化目标函数与约束条件

目标函数以加强梁截面形状为设计变量，定义为

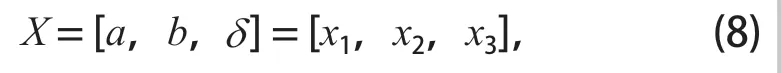
目标函数为

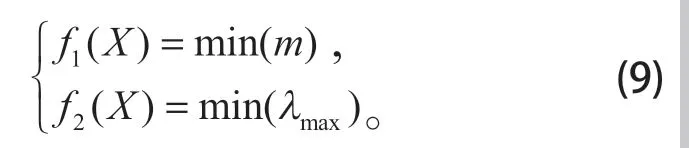
式中：m为驾驶室上部结构总质量；λmax为最大变形量。

约束条件包含强度约束、局部稳定性约束和边界条件约束，分别为以下约束函数

式中：[σ] 和 [τ] 分别为许用极限应力和许用切应力；[στcr]为许用复合临界应力。

4.4 优化结果分析

根据融合算法流程编写算法程序，其中设置算法迭代次数为 50次，学习因子c=2，最终得到该两目标优化问题的最终 pareto前沿分布示意图，如图 7所示。将实线部分连接的 5个最优解集数据整理，结果如表 2所列。

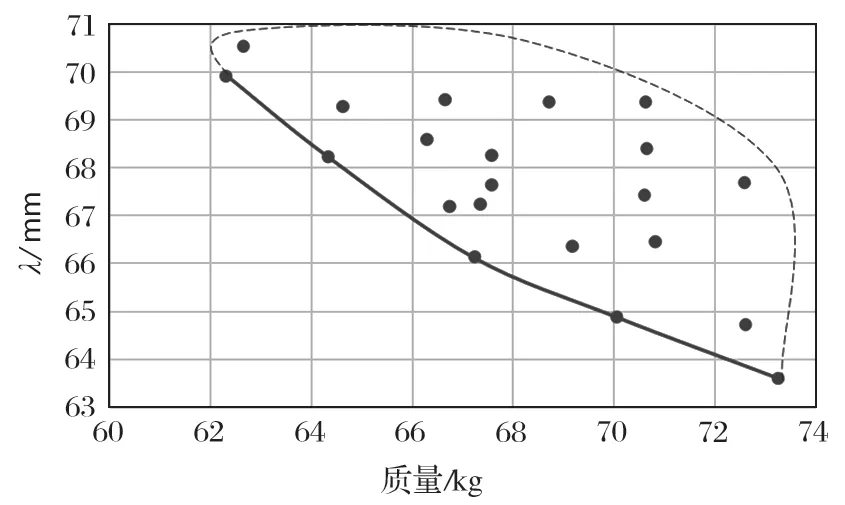
图7 优化最终 pareto前沿分布示意Fig.7 Final pareto frontier contours after optimization

表2 优化结果Tab.2 Optimization results

从图 7与表 2可以看出，优化目标函数之间互为冲突，即不可能使得结构质量与最大变形量同时达到最优解，因此对目标函数进行权衡协调，选取解集 3作为优化结果。将结果近似取整，确定最终优化参数为：a=40 mm，b=30 mm，δ=3 mm。优化后，驾驶室上部结构质量降低 41.90%，最大变形量降低了35.84%。

5 结论

(1) 以 WC8E胶轮车驾驶室为例，进行了 11 600 J冲击能量的落锤冲击试验，结果表明驾驶室在遭受落物冲击时，上部结构变形过大，容易对乘员造成挤压伤害。

(2) 以落锤冲击力峰值为静态载荷条件，对驾驶室上部结构进行了拓扑优化，根据拓扑结果确定了满足传力路径的优化结构方案。

(3) 基于粒子群与人工鱼群融合算法，对驾驶室上部结构加强梁参数进行了多目标优化，优化后上部结构质量降低 41.90%，最大变形降低了 35.84%。驾驶室结构安全性能显著提升，驾驶室上部结构质量降低，提高了整车的稳定性。