人情活动参与方的博弈行为研究

●孙 平

人情活动的核心内容就是人情支出，人情支出不仅包括金钱、实物支出等物质性支出，还包括人情活动参与方的情感与时间支出，这些支出在人们所处的不同经济社会环境中被支出方换算成效用单位，在排除非理性因素干扰的情况下，人们通过对效用的度量、比较来决定人情支出。但在近年来人情支出呈现逐渐背离人际交往的正常感情投资这一内涵，逢年过节、婚丧嫁娶、添丁增岁、评先选优、升学拜师、招工参军、看病求医、乔迁新居等事事必庆，受困于周遭人群的共同行为倾向，人情支出也在不断攀比中节节攀升，不仅影响了人际关系的正常维持，也对民众的幸福感产生了不利影响。这一背景为对人情活动的分析提出了现实需要，本文根据人情活动参与方行为特点与人情支出方的从众倾向，采用博弈论方法进行分析，具体运用静态博弈与进化博弈分析方法对人情活动举办参与过程，人情支出水平的决策过程进行分析，进而分别确定在何种条件下博弈方会决定是否举办、参加活动，确定高低人情支出水平的选取。

一、研究综述

国内对于人情活动有关研究主要集中在人情支出对居民幸福感、消费、社会资本的影响，以及这种影响在差异化群体中是否存在差异性等。

“人情”是一种社会情感的表现，是人们日常生活中不可或缺的一部分，作为维系“人情”的重要方式，人情支出扮演着增进社会幸福的重要角色（曾起艳）。但其绝对数额、收入占比的不断攀升使得人情支出不仅没有起到提升民众幸福感的作用，反而在很多情况下损害了民众的幸福感。人情支出具有刚性，隐蔽性强，求取回报的特点，其水平的决定在不同收入群体间是不同的，高收入群体为收入决定，而低收入群体还会受到高收入群体示范作用的影响（杭斌）。在人情支出影响的城乡差异方面，城镇地区人情支出能够作为“投资”起到提升长远利益的作用（杭斌），农村地区的人情支出积极作用体现在能够巩固发展社会网络，降低生产生活中的部分交易成本，如可以降低劳动力供求信息不对称下的搜寻成本，降低获取规模化土地的流转费用等（田学斌）。高人情支出同样对民众产生了诸如消费挤出等不利影响，但该结论并不统一，周广肃指出人情支出水平的适度提升有助于提升民众消费倾向，促进消费，而杭斌指出人情消费对中低收入人群的消费利大于弊。国内对于人情活动的分析鲜有采用博弈论方法进行，本文对基于人情活动中的存在的群体决策，示范效应特点，借鉴俞林在互联网金融监管博弈的分析方法分析人情支出水平决定，同时分析人情活动举办、参与的博弈活动，丰富本文的研究内容。

二、人情活动参与主体的博弈行为分析

人情活动的参与博弈主体包括活动的举办者、受邀者以及具有相同条件的博弈方1、2作为人情支出方。博弈活动方面可以分为两部分，一部分为在发生婚丧嫁娶，乔迁新居等庆祝或哀悼事项发生时涉事方是否举办相应人情活动，另一博弈方作为受邀者决定是否参与人情活动，另一部分为作为人情支出的两个博弈方决定采取高人情支出还是低人情支出的博弈。具体分析如下。

（一）人情活动举办者与受邀方的博弈行为分析

发生人情活动时，涉事方决策除会受到个人情感影响外，还会受到活动举办的成本收益水平影响，本文的分析内容将只根据博弈参与者的成本收益状况进行博弈分析。

参数设置与假设：参与方包括举办者与受邀方，假设涉及人情活动的事项发生而人情活动是否举办尚未确定时，博弈双方均知晓所涉事项的发生并且除举办者外的所有预计进行人情支出的主体在活动举办时均会成为受邀者。参数设置方面，活动参与方支出水平方面的参数设置包括举办者举办活动时需支出e水平的成本，不举办时成本为0（e>0），参加者参加有机会成本，设为f，参加者的人情支出设为g；收益方面参数设置包括受邀方参加有收益h，不参加收益0，举办者举办收益为i，不举办有k（i>k）。以上成本收益水平均代表相应物质精神成本效益对应的效用。受邀方不参加时，活动不举办。

基于博弈方对双方博弈策略的了解，本博弈采用静态博弈方法，得益矩阵如表1所示：

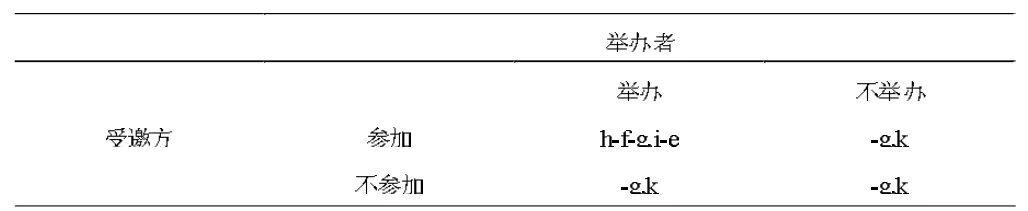
表1人情活动博弈双方得益矩阵

当h-f＞0，i-e＞k，时，即在受邀方参加的收益（如享受款待）大于参加的机会成本（如挤占的闲暇）并且举办的净得益大于不举办的得益的情况下，该静态博弈有两个纳什均衡（参加，举办）（不参加，不举办），其中后者效率劣于前者，并且该纳什均衡非严格稳定的纳什均衡，可以推断（参加，举办）将更可能是该博弈的最终决策策略组合，若该博弈重复多次进行，由于（参加，举办）这一纯策略纳什均衡具有严格稳定性，并且效率最优，可以预见该博弈不论是有限次亦或是无限次重复均不会改变该均衡解，仍为该均衡策略的重复。

当h-f＜0，i-e＜k时，（不参加，不举办）成为该博弈的唯一纯策略纳什均衡，该纳什均衡将会成为本博弈的均衡解，有限次重复博弈与无限次重复博弈因本博弈仅有单一纯策略纳什均衡，且不存在效率改进的策略组合，结论不变。h-f＞0，i-e＜k与h-f＜0，i-e＞k，两种情况与之类同，不再赘述。

（二）人情支出方的博弈行为分析

根据博弈方的群体决策特点，本节分析采用进化博弈方法。

参数设置与假设：本节假设博弈主体具有相似的特征。参数设置方面，支出水平参数设置包括高人情支出设为a，低人情支出设为b（a>b），收益水平方面包括在差异化策略下，高人情支出一方收益为c，低人情支出一方收益为0，相同策略下，双方得益均为d，（c>d）。策略选择方面，x采取高人情支出的概率，（1-x）采取低人情支出的概率。双方得益矩阵如表2所示：

表2人情支出博弈双方得益矩阵

博弈个体采取两种策略的期望得益分别为：U1=（d-a）*χ+（c-a）*（1-χ），U2=-b*χ+（d-b）*（1-χ），期望收益为U=χ*U1+（1-χ）*U2。

应用策略1的复制动态方程，可得到：

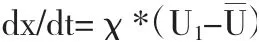
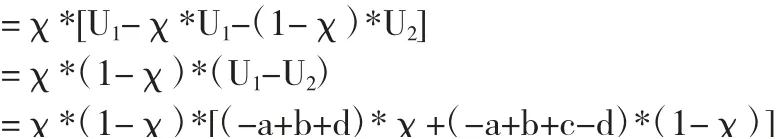
令F（x）=dx/dt，且令F（x）=0，可得χ*1=0，χ*2=1，χ*3=（-a+b+c-d）/（c-2d）三个可能的稳定状态，对F（x）分别在三个可能的稳定点处求导得F'（0）=-a+b+c-d，F'（1）=a-b-d，F'（χ*3）=[（a-b-c+d）*（a-b-d）]/（c-2d）。

当（a-b）＜（a-b），c＞2d时，即差异化策略下高人情支出方获得的较高得益（如更好的招待，关系变得更加密切等）与相同策略时的普通得益（相同的招待，关系维持原状等）的差值高于高人情支出相比低人情支出多付出的成本且差异化策略下高人情支出方获得的较高得益大于相同策略下的普通得益两倍的情况下F'（0）＜0，χ*1=0是一个进化稳定策略，即全部采取低人情支出。

当（a-b）＜d，c＞2d时，即高人情支出相比低人情支出多付出的成本小于策略相同时的普通得益且差异化策略下高人情支出方获得的较高得益大于相同策略下的普通得益两倍时，F'（1）＜0，χ*2=1为进化稳定策略，所有策略方都将采取高人情支出。

当（c-d）＞（a-b），（a-b）＞d,c＞2d时,有F'（0）＞0，F'（1）＞0,F'（χ*3）＜0,χ*3=（-a+b+c-d）/（c-2d）为进化稳定策略，根据χ*3与0.5的大小关系，可以确定全社会采取高人情支出与低人情支出人群的比例。

三、结论

（一）活动收益与机会成本决定人情活动的发生

人情活动涉事方的活动决策离不开人情活动收益的水平，较高的活动收益水平能够给活动受邀方与举办方提供更高的效用水平，而较低的收益水平很可能让活动“无利可图”甚至亏损，同时也会让受邀方参与活动的积极性降低。除人情活动的收益外，另一个重要的影响因素是参与的机会成本，受邀方参与活动总是伴随着闲暇的挤占，其他活动的推迟等负面影响，这些负面影响导致了受邀方的效用损失，也即参与活动的机会成本，较高的机会成本会让受邀方参与活动的意愿降低，其意愿的降低也将会影响人情活动的发生，而较低的机会成本则会让参与活动的正效用凸显，提升人情活动的发生频率，也会带来人情支出水平在总量上的提升。

（二）差异化策略得益差值与人情支出水平差值决定人情支出水平

正如前文分析所示，本文假设在博弈方策略存在差异的情况下，人情支出水平与效用回报呈正比，相比于低人情支出水平，博弈方在高人情支出水平上多付出的成本若高于相应的收益增量，则博弈方单独采取高人情支出水平会“得不偿失”，而同时采用高人情支出水平与同时采取低人情支出水平带来的效用回报相等，这时博弈方统一采取低人情支出水平就成为进化稳定策略，人情支出负担将会降低。若情况与之相反且高人情支出方相比于低人情支出方多付出的成本小于较低的均衡得益水平，也即多付出的成本不会太高，这时博弈方将采取统一高人情支出水平的进化稳定策略，人情支出负担将保持在高位水平。如出现与前述两种情况相悖的现象发生，社会群体决策将出现高人情支出与低人情支出并存的情况。在本文的分析结论中以上策略结果的出现均要求差异策略高回报一方的得益大于同样策略下得益的两倍。