数形结合思想在高中物理解题中的应用
◇ 福建 冯顺荣
数形结合思想是一种可使复杂问题简单化、抽象问题具体化的数学思想方法,其在物理问题分析中的应用,更多地体现在物理规律与物理图象之间的一一对应关系上,或以“数”辨“形”,或以“形”变“数”.其中“数”是分析问题的灵魂,“形”是数的直观外化,二者相辅相成,是抽象思维和形象思维的有机结合.灵活运用数形结合的方法,可使题目中的隐含条件在“数”与“形”的相互转化中渐次浮出水面,从而使复杂的物理问题迎刃而解.
1 以“数”辨“形”
物理量间的数量关系,决定了物理图象的特点,对于图象辨析选择问题,以此为切入点,由“数”辨“形”,即可选出正确的选项.
例1如图1所示,小球从光滑斜面上某高度处由静止释放,从斜面滑下来后进入一段光滑水平面然后做平抛运动落到另一斜面上.多次改变小球的释放高度h 发现小球平抛运动的位移L 随h 的变化而变化.若小球经过斜面和平面转折处的速度大小不变,关于L 随h 变化的图象正确的是( ).
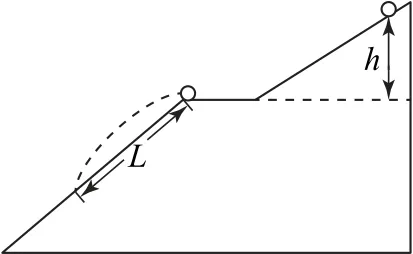
图1
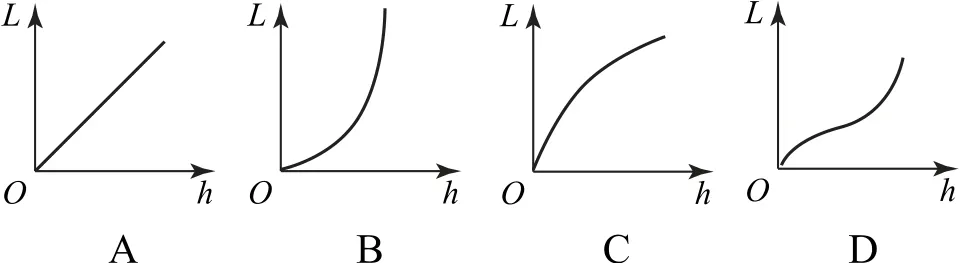
设小球下滑到上斜面底端时的速度为v0,由机械能守恒定律得设下斜面的倾角为α,小球从水平面飞出后做平抛运动,则有水平方向有Lcosα=v0t,竖直方向有联立解得可知L 与h 成正比,选项A正确.
本题分析的关键是从题目已知条件出发,在过程分析的基础上,运用机械能守恒定律和平抛运动规律,推导出L 随h 变化的关系,即由“数”辨“形”,从而使问题得以顺利解决.
2 以“形”变“数”
涉及定量计算问题时,要寻找与图象对应的物理关系式,以“形”变“数”,从“数”的角度明确图象斜率、截距、面积表示的物理意义,从而突破分析问题的瓶颈.
例2如图2所示,质量m=1kg的物体以v0=4m·s-1的初速度从水平面的某点向右运动并冲上半径R=0.1m 的竖直光滑半圆轨道,物体与水平面间有摩擦.设出发点到N 点的距离为x,物体从M 点飞出后,落到水平面时落点到N 点的距离为y,作出x随y2变化的关系如图3所示,求物体与水平面间的动摩擦因数μ.
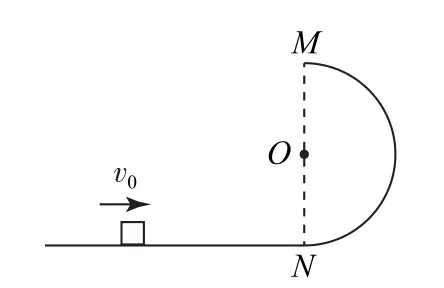
图2
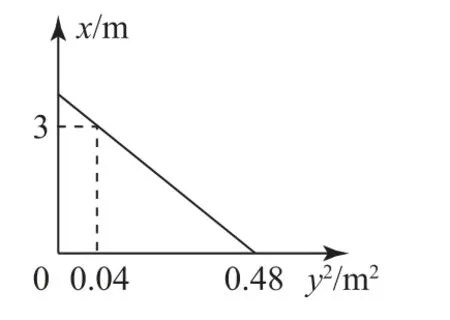
图3
本题给出了x 和y2的图象,虽形象直观,但μ 与图象间的关系却是隐性的,如何挖掘μ与图象间的关系,是求解问题的关键;只有运用相应的运动规律正确地将题中图形用“数”表达出来,实现数与形的有效对接,才能将问题顺利解决.
总之,在高中物理中,数形结合的思想,其实质是抽象物理规律与直观图象的结合,物理关系与物理图形之间的相互转化是分析问题的关键;在具体应用中,要眼中有“形”,心中有“数”,只有把握好与物理规律密切相关的“数”的实质,实现“数”与“形”的有效对接,才能探究题目的深层内涵,从而优化解题途径,提高解题效率.

