某隧道超挖条件下应力应变模拟分析

赵福利

（珠海市建设工程质量监测站 珠海519015）

0 前言

随着隧道工程的大规模建设，由于工程地质和施工因素的限制，围岩的超欠挖现象比较普遍，而研究隧道超欠挖对研究超欠挖引起的应力重分布、隧道围岩变形及稳定性具有重要意义。

诸多学者对隧道超欠挖现象进行了研究。刘建民等人［1］运用数值模拟的方法分析了不同超挖位置、超挖深度、超挖数量等对洞室围岩稳定性的影响；王明年等人［2］用自适应有限元法研究了超欠挖对隧道稳定性的影响；王明年等人［3，4］用理论和数值方法定量地分析了平面应变状态下超挖对圆形和直墙拱型隧道围岩应力状态的影响；丁泰山［5］采用有限元软件针对直墙拱型断面，研究了超欠挖对围岩受力的影响；马云峰［6］针对城门洞型隧道断面形式，采用数值仿真试验的方法进行了二维平面分析，研究了不同超挖高度、不同混凝土喷层厚度、不同围岩级别等条件下超挖，对围岩位移场产生的影响；靳天成［7］用有限元方法，分别研究了拱顶、拱肩部位超挖对围岩变形和围岩应力的影响；刘明才［8］根据喷射混凝土层厚度，将超欠挖下围岩边界分为三类，再基于厚壁圆筒理论和并联原理，推导锚喷支护系统的力学特性，利用收敛-约束法分析隧道超欠挖情况下围岩的稳定性；朱林［9］从理论分析与数值模拟两方面开展研宄，分析超欠挖状态下支护结构的力学特性和超挖对围岩稳定性的影响；耿晓杰等人［10］根据隧道开挖断面轮廓具有分形特征的特点，计算了鸳鸯会隧道20个典型断面轮廓分形维数，研究了围岩质量与超欠挖的关系，得出围岩质量多因素修正指标与超挖比及断面轮廓分形维数呈线性关系，随着围岩质量多因素修正指标的提高，超挖比和断面轮廓分形维数将降低，并根据复相关原理，建立了三者间的复相关关系，为隧道围岩质量的正确评价及超欠挖分析提供有益参考。本文采用ABAQUS 软件，通过对珠海市某隧道SD1 断面进行数值模拟分析，研究了超挖高度对隧道拱顶的施工变形和应力变化的影响。

1 工程概况

珠海市某隧道大跨段里程为左ZK1+155～ZK1+370（长L=215 m）、右YK1+166～YK1+430（长L=264 m），其中SD1 衬砌断面适用里程为ZK1+155～ZK1+203、YK1+166～YK1+222，其最大开挖高度16.32 m，最大开挖跨度达28.23 m，断面面积大于360 m2，其主要地质结构为花岗岩，围岩级别为Ⅲ级围岩，开挖方法为两台阶法。

本文以该隧道SD1 断面为例，建立二维隧道模型进行数值模拟分析，研究在超挖宽度为6 m时，不同超挖高度对隧道围岩变形及应力变化的影响。因为只考虑开挖后土体的变化情况，所以没有模拟支护情况，隧道埋深91 m。

2 有限元模型的建立

依托该隧道SD1 断面，建立二维有限元模型如图1a 所示。二维有限元模型长270 m，宽160 m，计算采用大型有限元软件ABAQUS 进行模拟分析，共有2 570 个单元，计算所使用的ABAQUS 所提供的CPE4二维四节点平面应变单元。计算模型约束条件为左右两侧施加水平方向的单位位移约束，下侧施加竖直方向的单位位移约束，上侧为自由端。施加荷载为重力荷载。模型计算采用的材料参数为：岩体弹性模量4.72 GPa，泊松比0.3，内摩擦角37°，黏聚力0.7 MPa，土体密度2 560 kg/·m3。图1b为简化的隧道模型。

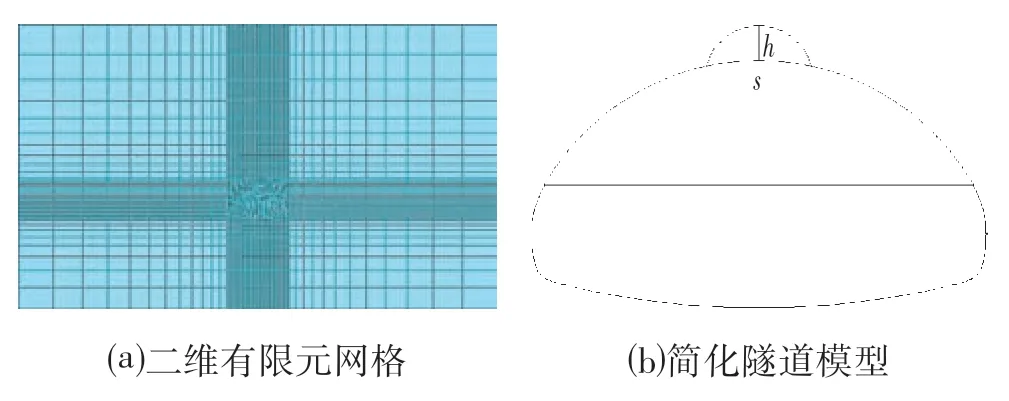
图1 二维有限元网格模型及简化隧道模型Fig.1 2D Finite Element Mesh Model and Simplified Tunnel Model

3 计算结果分析

分析超挖高度的影响，选取超挖宽度为6.0 m。超挖高度选取0.0 m、0.4 m、0.8 m、1.2 m、1.6 m、2.0 m共6种工况。超挖位置为拱顶且沿隧道中轴线对称分布，研究隧道施工过程中，不同超挖高度对围岩变形规律和受力特征的影响。

3.1 位移分析

图2 为未超挖工况和超挖高度2.0 m 工况的竖向位移云图，由于各工况云图形状大致相同，最值分布位置相近，因此只给出未超挖工况和超挖2.0 m 工况的云图进行对比。为了更直观有效地研究超挖对围岩位移的影响，选取地表、拱顶等特殊点进行分析，观察其位移变化规律。

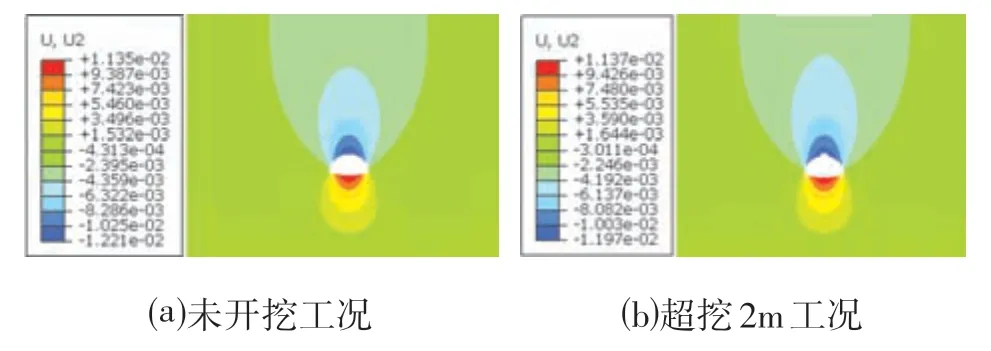
图2 拱顶沉降云图Fig.2 Vault Settlement Nephogram

图3a为地表沉降曲线图，选取拱顶所对应地表点左右各20 m 范围内的特征点进行分析。从图3 中可以看出，各工况地表沉降值沿拱顶所在中轴线对称分布，且越靠近拱顶所对应地表点，沉降值越大，各工况最大沉降值均位于拱顶所对应地表点。同时超挖高度不同，地表沉降值也各不相同，当超挖高度为0.4 m时，地表沉降值最大，超挖高度为1.6 m 时，地表沉降值最小。沉降值总体呈现先增加后减小再增加的规律。

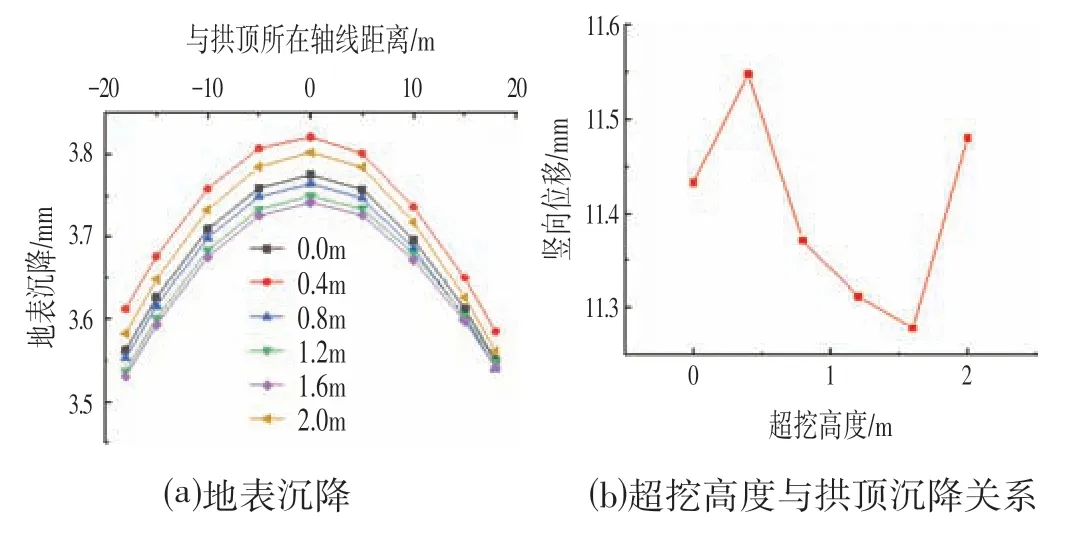
图3 沉降曲线Fig.3 Settlement Curve

由于拱顶处超挖时，原设计轮廓线上拱顶沉降最大的点会被挖掉，各工况无法直接比较超挖对拱顶沉降产生的影响，因此选取拱顶正上方2 m 处的同一点进行观测。表1为各工况拱顶沉降。图3b为观测点的竖向位移随超挖高度变化的曲线，可以看出，刚开始，超挖高度小于0.4 m时，竖向位移随超挖高度的增加而增加，在0.4 m时达到最大值，为11.547 5 mm。随着超挖高度的增加，观测点的竖向位移随之减小，在超挖高度为1.6 m 时，竖向位移达到最小值，为11.278 1 mm。之后拱顶沉降值又随之增大。

表1 各工况拱顶沉降Tab.1 Settlement of Vault under Various Working Conditions

3.2 主应力分析

图4 为部分工况下隧道最大和最小主应力云图，从中可以看出，隧道在拱顶、拱肩、边墙位置产生较为明显的应力集中现象，并且各工况下最大和最小主应力都在边墙位置取得最大值，超挖2 m 工况时边墙最大主应力明显向下扩散。而在隧道底板位置有少量的拉应力区域，这会对隧道的稳定性产生一定的影响。所以在隧道施工过程中，应对这两部分岩体实施加固，注意其稳定反应，防止该部分发生破坏。

通过提取云图中的数据绘出围岩拱顶应力值图（见图5）。从图5 中可以看出，在未超挖时，拱顶的最大主应力值还很小，超挖开始后拱顶最大主应力值会逐渐增加，当超挖高度为1.2 m 时，最大主应力值达到最大值，为131.127 kPa，与未超挖时相比，增大了将近75%。然后随着超挖高度的增加，拱顶的最大主应力值会随之减小。

同时，随着超挖高度的增加，拱顶的最小主应力值随之增大，两者呈正相关关系。这与最大主应力先增加后减小的规律不相符合。超挖开始时，最小主应力值增大，但曲线斜率较小，增大幅度有限，但当超挖高度大于0.4 m 时，曲线斜率变大，当超挖高度达到2.0 m时，最小主应力值达到最大，为1 085.79 kPa。

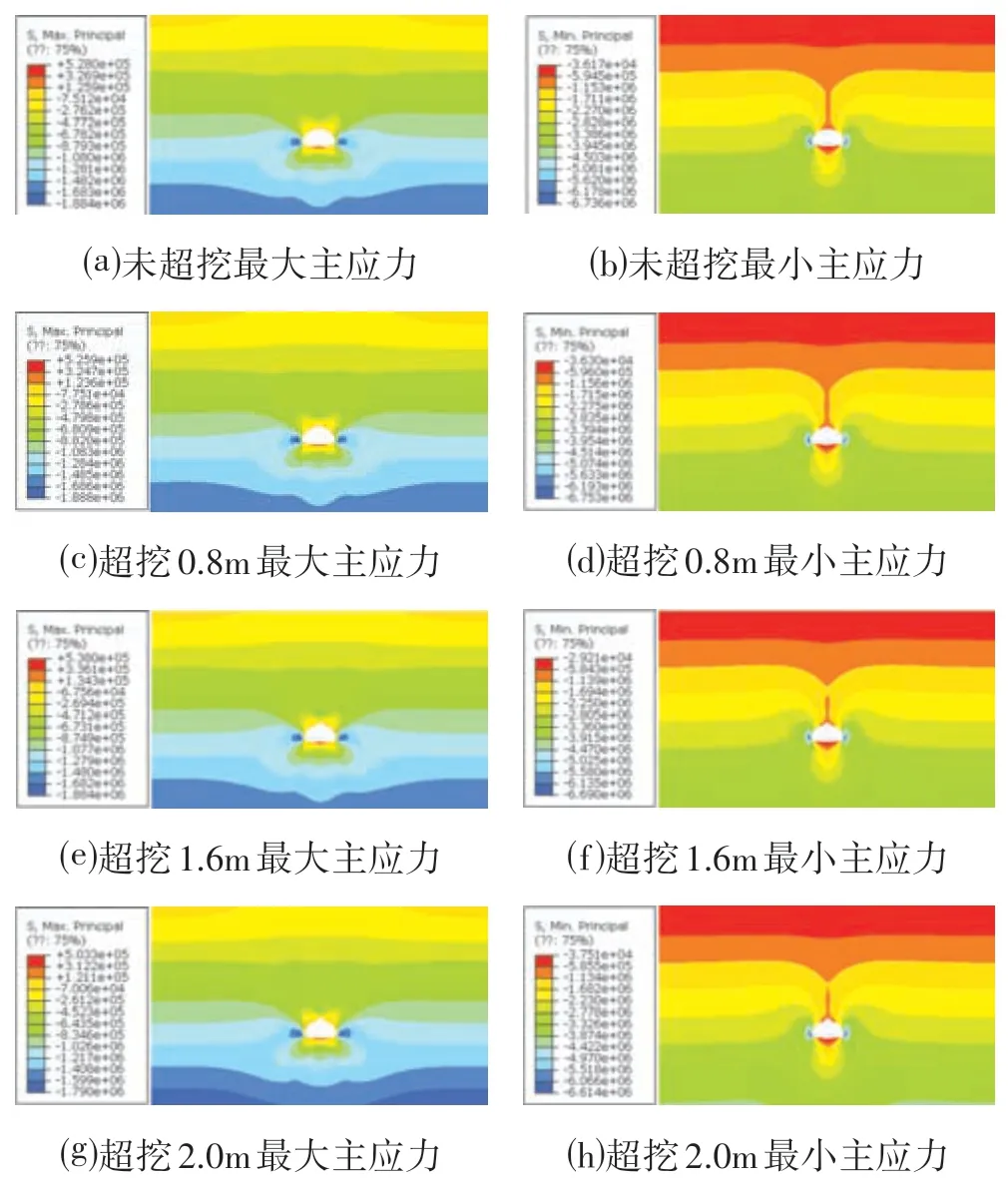
图4 各工况主应力云图Fig.4 Main Stress Cloud Diagram of Each Working Condition

图5 各工况拱顶主应力值Fig.5 Principal Stress Value of Vault of Each Working Condition

由于在实际开挖过程中，超挖不仅仅发生在拱顶位置，而是在拱顶、拱肩和边墙都存在超挖，且超挖情况更加复杂多变。本文只是以拱顶为例，从数值模拟的角度分析超挖情况下隧道的应力与应变情况。

4 结论

⑴从围岩位移上来看，拱顶超挖对沉降的影响较小，随着超挖高度的增加，拱顶沉降值先增加后减小再增加，并不是正反比例关系，并且会沿土体传导至地表，因此需要对隧道围岩位移变化情况进行实时监控，注意拱顶部位的沉降，必要时适当减少炸药用量，科学合理地实施爆破。

⑵从围岩应力上看，拱顶超挖会在隧道拱顶、拱肩及边墙位置产生较为明显的应力集中现象。并且超挖高度越大，应力集中现象越明显。同时，随着超挖高度的增加，拱顶的最大主应力先增大后减小，而最小主应力则线性增加，两者规律并不相同，这会对隧道稳定性产生一定影响。因此在施工过程中，应密切注意围岩应力的变化，避免因超挖造成隧道的局部破坏。