某超高层混合结构基于增量动力分析的地震易损性分析

李定环，邓 晖，胡志光，傅冠翔，胡文魁

（1、中铁建工集团诺德投资有限公司 深圳518048；2、华南理工大学 广州510641；3、深圳市地铁集团有限公司 深圳518026）

0 引言

20 世纪70 年代，地震易损性分析首次应用于结构的抗震性能评估［1］。当时计算机技术尚未普及，地震易损性分析主要依赖判断法和经验法。判断法主要依赖于专家的个人水平和工程经验，由美国学者Whiteman 等人［2］于1974 年提出。经验法是基于大震发生后的震害调查，对震后房屋的损伤程度进行整合后得到地震易损性曲线和矩阵，对于多震害国家此方法较容易实现。

随着计算机技术的不断进步，动力弹塑性分析已能成功运用在建筑结构的抗震分析中，因此基于动力弹塑性分析的增量动力分析方法（Incremental Dynamic Analysis，IDA）得到了越来越多的关注。该方法是对所分析的结构进行大量的时程分析运算，得到大量的样本数据，然后通过数学方法分析结构在不同地震动强度下的超越概率，即可得到该结构的地震易损性曲线和矩阵。

本文对深圳某超高层混合结构进行基于IDA 的地震易损性分析，对结构进行基于概率的抗震性能评估，为工程应用提供参考。

1 原理简介

1.1 增量动力分析

增量动力分析法（Incrementa Dynamic Analysis，IDA）是目前基于性能地震工程（Performance-based Earthquake Engineering，PBEE）中用于确定结构在不同强度地震动作用下反应的最有潜力的一种方法［1］。该方法的基本原理是对结构输入乘以不同比例因子的一条或多条地震动记录，这些地震动记录由于不同的比例因子已经成为了具有多重强度的一系列地震动记录；通过结构的动力弹塑性分析可得到结构在这一系列地震动记录下的非线性响应；选择合适的地震动强度指标IM 和结构性能指标DM，对计算得到的数据进行后处理，即可得到以IM 为自变量，以DM 为因变量的IDA 曲线，每一条地震动记录会对应一条IDA曲线，多个地震动记录的多条IDA 曲线称之为曲线簇；通过IDA 曲线簇，采用统计方法即可从概率意义上评估结构在不同强度地震动作用下的抗震性能。

增量动力分析的基本步骤如下［3］：

⑴建立结构的弹塑性分析模型，且要使用一定的方法对模型的合理性进行验证，保证模型能够正确合理地反映结构在地震动作用下的响应；

⑵根据研究或工程需要选取一定数量的地震波组成增量动力分析波组，并确定地震动强度参数IM和结构性能参数DM；

⑶根据工程实际需要和模型复杂程度确定合适的调幅方法，并确定IDA曲线的极限状态；

⑷将每条地震波按照事先确定好的调幅方法，处理后输入结构进行弹塑性时程分析，并根据确定好的IDA 曲线极限状态判定是否继续计算，最终得到IDA曲线簇；

⑸对IDA 得到的计算数据按照一定的数学方法进行处理，得到对结构进行抗震性能评估需要使用的结果。

1.2 地震易损性分析

地震易损性分析是计算结构在不同强度地震作用下结构达到或超过某种极限状态的条件概率，所以增量动力分析的计算结果成为了地震易损性分析的基础。

基于增量动力分析的地震易损性分析步骤如下［4］：

⑴ 建立结构的弹塑性模型；

⑵选择能满足分析需要的多条具有代表性的地震动记录，并选择合适的地震动强度参数和结构性能参数；

⑶ 进行增量动力分析并提取样本数据，绘制IDA曲线簇；

⑷量化极限状态LS 与结构性能参数之间的关系，得到基于结构性能参数的极限状态定义；

⑸设某极限状态LSi对应的结构性能参数为edpi，则在地震动参数IM=x时，结构响应EDP超过edpi的概率可表示为：

文献［5］和文献［6］认为，EDP 对IM 的条件概率分布符合对数正态分布，则有

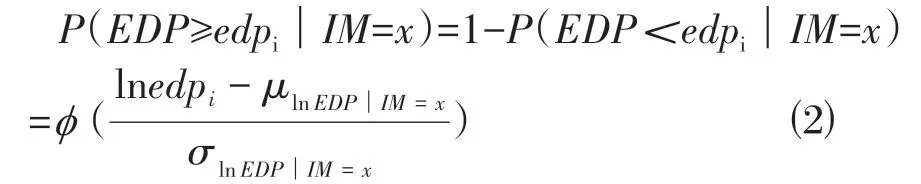
⑹以IM 为横轴，P（LSi|IM=x）为纵轴，绘制结构的地震易损性曲线，得到结构的地震易损性矩阵；

⑺进行结构的易损性评估。

2 算例

2.1 结构基本信息

深圳某超高层位于深圳北站附近，包含1#、3#主楼和2#、4#裙房。其中1#主楼地下3 层，地上58 层，结构高度248.75 m。工程所在地区抗震设防烈度为7 度，建筑场地类别为Ⅱ类，设计基本地震加速度值为0.10g，设计地震分组为第一组，场地特征周期为0.35 s。1#主楼采取钢框架-钢筋混凝土核心筒混合结构体系，并在12～16 层、24～28 层、35～39 层、46～50 层设置斜柱实现外框架相对于核心筒斜切角式的缩进，表现出建筑旋转向上的效果。部分楼层的结构平面布置如图1所示。

图1 部分楼层结构平面布置Fig.1 Structural Floor Plans of Some Floors

2.2 模型的建立

从计算效率和精度两个方面综合考虑，本文选择PERFORM-3D 进行结构的增量动力分析。梁柱构件采用塑性区模型进行模拟，混凝土梁划分为12 条纤维，其中2 条钢筋纤维和10 条混凝土纤维；将钢梁划分为12条纤维，其中两翼缘各1条，腹板10条；钢管混凝土柱划分为48条纤维，钢管划分为12条纤维，混凝土划分为36 条纤维；而塑性区的长度则参考文献［7］的建议取为截面高度的0.5 倍。剪力墙构件采用shear wall宏观单元模拟，沿截面高度混凝土和钢筋各分配8条纤维，沿墙肢高度每层划分一个单元。

为了在PERFORM-3D 中准确地建立结构的弹塑性分析模型，先使用YJK 软件按照该工程实际施工图进行建模和荷载的施加，然后进行计算得到结构的模态与配筋结果，并根据施工图对剪力墙等部分主要构件的配筋结果进行修改，为PERFORM-3D 弹塑性模型的建立与校核做好准备。算例结构的YJK 模型和PERFORM-3D模型如图2所示。

PERFORM-3D 模型的几何信息、配筋信息、荷载信息以及质量源信息都应该与YJK 模型的数据接近，且在墙单元中设置了内嵌梁来模拟墙和连梁的刚接状态，故需要对比2 个模型的模态结果来验证转换的模型是否与原模型存在较大偏差。前三阶模态对比结果如表1 所示。2 个模型的自振周期十分接近，说明PERFORM-3D 模型相比于原模型不存在较大的偏差，结构整体的各项信息在合理范围内，可以用于结构的动力弹塑性分析。

图2 算例结构模型Fig.2 Modals of Example Structure

表1 前三阶模态对比Tab.1 Comparison of the First Three Modals

2.3 地震波选择

基于大量的强震观测记录的分析，《建筑抗震设计规范（2016 年版）：GB 50011-2010》［8］规定设计地震动用弹性加速度反应谱表示，设计特征周期则定义为“抗震设计用的地震影响系数曲线中，反映地震震级、震中距和场地类别等因素的下降段起始点对应的周期值［9］。当选择地震波数量较多时，根据地震动的特征周期与场地特征周期接近这一方法选择地震波是可以从平均意义上得到较符合工程所在场地特性的地震波。

根据上述内容，本文选择特征周期与场地特征周期接近的地震波，同时满足《高层建筑混凝土结构技术规程：JGJ 3-2010》［10］中有效时长的要求。为保证增量动力分析的随机性，不选取来自同一次地震不同测站的记录。本文共选取12条天然地震波，并生成了3 条人工地震波用于结构的增量动力分析，地震波信息如表2所示。

2.4 增量动力分析

目前较最常用的地震动强度指标是PGA 和Sa（T1，ξ），而Sa（T1，ξ）并不适合用于长周期超高层结构。PGA 概念简单，是地震动时程记录获取后就可以直接获得的指标，我国规范也选定PGA作为地震动强度指标，故本文采用PGA 进行调幅计算。考虑到文献［8］中9 度烈度区罕遇地震加速度时程最大值为620 gal，且可能会发生的“特大地震”，所以此次IDA 分析的PGA 上限取为1 000 gal，且为了在得到较精确的结果的同时提高计算效率，PGA 调幅按照50 gal、100 gal、200 gal、300 gal、400 gal、600 gal、800 gal、1 000 gal 进行。在400 gal之前，考虑到结构由弹性逐渐进入弹塑性阶段，构件强度及刚度均有不同程度的退化，步长过长会导致这一阶段的计算值不准确，所以调幅步长较小。地震动加速度峰值在400 gal 之后已属于非常罕遇的地震，发生此类大地震的概率很小，且考虑到结构弹塑性模型在进入塑性程度较高时，每次非线性时程分析会耗费大量时间，所以在综合考虑这两点因素后适当增加步长。

表2 结构增量动力分析地震波信息Tab.2 Seismic Wave Information of IDA for Structure

在PERFORM-3D 中，模态阻尼与瑞利阻尼是叠加的，故采用统一的模态阻尼加较小的瑞利阻尼来模拟结构的阻尼，模态阻尼统一取0.04。在进行弹塑性分析时，考虑包括静力荷载在内的P-△效应，初始荷载考虑DL+0.5LL的重力荷载，并分10步加载于结构，积分步长取0.02 s。每条地震动按照规范建议采用双向地震动输入，X向和Y向的地震波峰值取为1∶0.85。

3 算例的地震易损性分析

3.1 结构极限状态LS的确定

结构抗震性能目标是针对某一级地震设防水准而期望建筑物能够达到的性能水准或等级，是抗震设防水准与结构性能水准的综合反映。文献［10］中关于抗震的性能设计规定了4 个抗震性能目标和5个性能水准等级。4 个抗震性能目标为A、B、C、D 四个等级，5 个性能水准等级为完好（无损坏）、基本完好（轻微损坏）、轻度损坏、中度损坏和比较严重损坏。在进行地震易损性分析时，各项结构的极限状态的确定以及指标的量化，也应参考文献［10］中的有关规程进行。但是针对不同的结构体系，指标的量化程度也会有所不同。

本文的结构极限状态LS确定的思路如下：

⑴ 性能水准与继续使用的可能性：除采用文献［10］规定的5 个性能水准等级之外，参考国内外文献的做法，再增设性能水准等级严重损坏。严重损坏的性能水准等级对应的继续使用的可能性为无法修复，是建筑物接近倒塌达到直接拆除条件的性能状态，若超过该极限状态则可认为建筑物发生了倒塌。

⑵层间位移角参考指标：参考文献［8］附录M 中表M.1.1-2 的示例，确定各极限状态下层间位移角限值。对于严重损坏这一性能水准，由于算例是钢筋混凝土和钢结构的混合结构，故取文献［8］中混凝土结构和钢结构塑性位移角限值的平均值。

⑶层间位移角限值：文献［8］规定的框架-核心筒结构的弹性层间位移角限值为1/800，塑性层间位移角限值为1/100。但本文算例属于高度超限的较复杂超高层结构，相较于规范限值应适当放宽，参考《超限高层建筑工程抗震设计指南（第二版）》［11］中的相关建议，取弹性层间位移角限值为1/500，塑性层间位移角限值为1/100。

用于本算例的性能水准及量化指标如表3所示。

表3 用于本文算例的性能水准与量化指标Tab.3 Performance Level and Quantitative Indicators for the Example Structure

3.2 地震易损性曲线的绘制

将结构经过各条地震动插值后得到的最大层间位移角θmax提取出来，运用数学方法计算每组地震动作用下θmax的对数期望和对数标准差，再根据各极限状态下的层间位移角限值，代入式⑵中即可计算出各极限状态下的易损性数据点，从而绘制出结构的易损性曲线如图3所示。

3.3 地震易损性分析结果

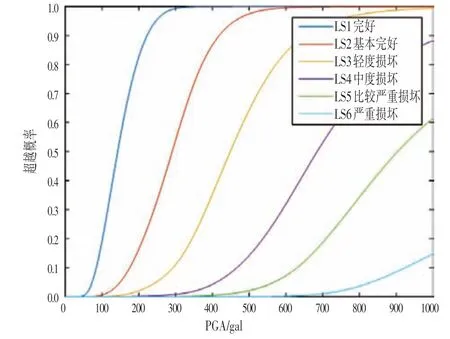
图3 结构的地震易损性曲线Fig.3 Seismic Vulnerability Curve of Structure

根据文献［10］要求对结构进行地震易损性分析与评估，可将地震易损性曲线转化为易损性矩阵。本文算例属于7 度区，设计基本加速度0.10g，故对于按照规范规定的7 度区（0.10g）对应的地震动PGA 转化为易损性矩阵如表4 所示。在7 度多遇地震水准下，结构在原场地地震动作用下超越完好极限状态的概率仅为0.01%，说明结构在小震作用下可以基本确定会处于无损坏的状态。在7 度设防地震水准下，结构超越完好极限状态的概率为19.28%，超越基本完好极限状态的概率为0.56%，说明在7 度中震作用下结构有可能会出现轻微的损坏，但大概率处于无损坏状态。在7 度罕遇地震水准下，结构超越完好极限状态和基本完好极限状态的概率为89.40%和22.57%，而超过轻度损坏极限状态的概率仅为3.10%，说明结构大概率会是基本完好的，只需稍加修理即可。从易损性分析也可以看出算例结构具有很强的安全储备，原因主要有3点：①本文选择原场地地震动时以特征周期为基准，选取从平均意义上代表算例结构所处的场地的地震动，并未完全贴合反应谱去选择地震动；②超高层结构的结构体系和截面尺寸一般受刚重比等强条控制，所以设计普遍偏保守；③算例所处地区深圳的基本风压较大，风荷载在结构设计时起到控制作用。

4 结语

本文以深圳某超高层1#楼为算例，使用PERFORM-3D 弹塑性分析软件对算例进行了基于增量动力分析的地震易损性分析。本文从模型的建立、地震波的选择、增量动力分析的实施、结构极限状态的确定以及易损性曲线的绘制几个方面，详细介绍了算例结构进行地震易损性分析的过程。

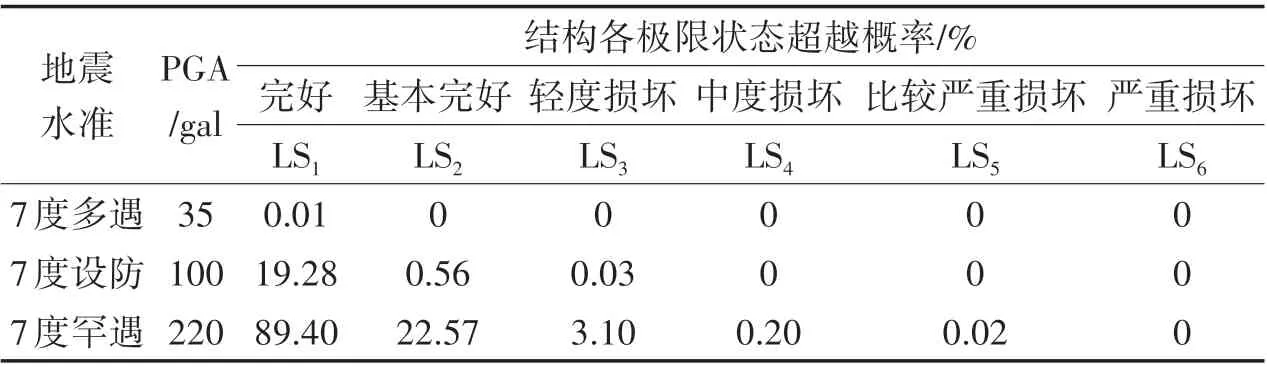
表4 结构的三水准地震易损性矩阵Tab.4 Seismic fragility Matrix for the Given Three Ground Motion Levels

通过结构的地震易损性分析可得到以下结论：

⑴在小震作用下结构基本确定会处于无损坏的状态，在中震作用下结构有可能会出现轻微的损坏，在大震作用下结构大概率是基本完好的，只需稍加修理即可。

⑵结构具有良好的抗震性能，满足文献［8］的三水准设防要求，具有很强的安全储备。原因主要有3点：①本文选择原场地地震动时以特征周期为基准，选取从平均意义上代表算例结构所处场地的地震动，并未完全贴合反应谱去选择地震动；②超高层结构的结构体系和截面尺寸一般受刚重比等强条控制，所以设计普遍偏保守；③算例所处地区深圳的基本风压较大，风荷载在结构设计时起到控制作用。