抛物线与直线铅垂差模型的最值问题

冯更发

【摘要】本文主要讨论在抛物线与直线背景下的铅垂差模型最值问题，我们可以得到：抛物线与直线的铅垂差，在有两交点的前提下，若自变量在两交点之间，则在交点的中点处铅垂差取得最大值。应用此模型，我们还可以解决相同背景下的三角形面积最值问题、四边形面积最值问题以及线段比值最值问题。

【关键词】抛物线   铅垂差   最值

几何教学是初中数学教学中一个重要组成部分，同时也是中考的热点和难点。新义务教育数学课程标准在课程设计理念中，特别强调注重发展学生的模型思想，使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程.模型教学不仅能够让学生拥有牢固的数学基础，更能培养学生的创造性思维，提升自身综合素质，为未来的良好发展打下良好基础。函数是初中数学重要的组成部分，它深刻的反映了客观世界的运动和实际的量之间的依赖关系，通过坐标系中的曲线上的点的坐标反映量变的关系。

在近几年各地中考中，几何最值问题屡屡受到命题者关注，此类问题不仅涉及平面几何的基础知识，还涉及几何图形的性质、平面直角坐标系、方程与不等式、函数知识等。常见二次函数作为压轴题出现，而二次函数和一次函数的结合，从形的角度来讲，是抛物线和直线的结合，是常考题型。这类试题较好地考查了同学们的几何探究、推理能力的要求及数学思想方法的运用。

一、铅垂差模型介绍

抛物线与直线的铅垂差，在交点的中点处取得最大值。

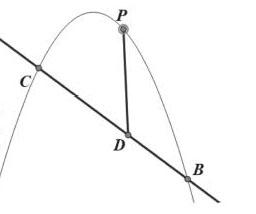
抛物线与直线交于B、C两点，点P为抛物线上BC部分间一点，过点P作PD垂直x轴交BC与点D，则当点D为BC中点时，线段PD有最大值。

二、模型探究

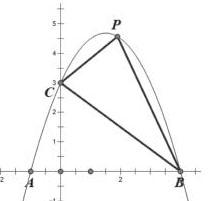
如图，抛物线y=-（x+1）（x-3）和直线y=-x+3交于点B（3，0）和C（0，3），P为抛物线上一点，已知点P在线段BC上方。过点P作PD⊥x轴交BC于点D。若P点横坐标为x，

（1）用x表示线段PD的长。

（2）当PD=0时，求x的值

（3）问当x为何值时，线段PD有最大值，最大值是多少？

模型解析：抛物线与直线的铅垂差，从数的角度来讲，就是二次函数减一次函数，结果依旧是二次函数。在交点之间，此二次的函数有最值。抛物线与直线的交点，就是新函数的值为0的点，而新函数的最值，根据二次函数交点式，在交点的中点处取得最值。

三、模型拓展应用

思路点拨

一般来说，抛物线与直线的铅垂差，从数的角度来讲，就是二次函数减一次函数，结果依舊是二次函数。在交点之间，此二次的函数有最值。抛物线与直线的交点，就是新函数的值为0的点，而新函数的最值，根据二次函数交点式，在交点的中点处取得最值。抛物线与直线上的点连线段的最值问题，可以通过相似转化为铅垂线段的最值问题，这里体现的是斜化直思想。与抛物线上的点和直线上的点的连线段比值有关的问题，也可以利用相似转化为铅垂线段的比值问题。