平面向量考点分析及应对策略

潘刚

【摘要】向量是既有大小，又有方向的量。这使得它具有数的特征，能够进行运算，同时它又具有形的内涵。有了向量以后，图形的平行、相似、垂直、距离等就可转化为向量的线性运算和数量积运算。向量特性使它天然的起着沟通代数、几何，三角函数、解析几何、复数的桥梁作用。

【关键词】平面向量   考点分析   应对策略

向量是既有大小，又有方向的量。这使得它具有数的特征，能够进行运算，同时它又具有形的内涵。有了向量以后，图形的平行、相似、垂直、距离等就可转化为向量的线性运算和数量积运算。向量特性使它天然的起着沟通代数、几何，三角函数、解析几何、复数的桥梁作用，是数学知识和数学思想方法的重要结点，是考生发展能力和解决问题的重要数学工具。

从近几年的高考试题来看，平面向量的考点主要有以下几个层面。

一、考查基本概念和基础运算

应对策略：本题主要考查向量線性运算，平行四边形法则、三角形法则及数乘向量、共线向量表示，属较易题型。要求考生掌握平面向量的和、差、数乘的定义和运算技巧，理解其几何意义。培养和提高读图识图能力，掌握平行四边形法则及变式是解决此类问题的关键。

二、考查平面向量本身的基本应用

此类题多以选择或填空题的形式出现，是高考中出现频率最高的向量考点。主要包括求向量的共线、垂直、模、夹角、坐标、数量积的问题。

应对策略：本题主要考查考生对平面向量基本定理、正交分解、向量坐标表示的迁移应用能力。只有对向量坐标表示有深刻的理解，才能自然的用i，j两个轴上的单位向量去替换a，b向量，从而简化计算的过程。迁移能力和化归思想的培养，往往是创新思维的火种。

三、考查向量与几何图形、解析几何的结合

特别是向量与三角形、四边形、圆等的结合，此类题主要考查对向量线性运算、向量坐标运算、参数方程、三角函数、函数最值、不等式等的综合运用，对数学思想方法，尤其是对数形结合的方法要求较高，有一定的难度。

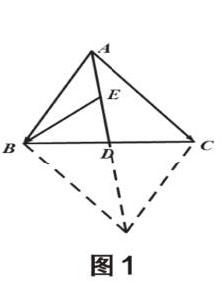
例3（2017年全国Ⅱ卷 理科数学第12题）已知⊿ABC是边长为2的等边三角形，P为平面ABC内的一点，则PA·（ PB + PC）的最小值为（    ）.

应对策略：本题主要考查向量的坐标法，向量的数量积的坐标表示，体现了数与形相互转化的和密切结合的思想，最后将向量问题转化为代数问题。将向量问题翻译成代数问题是解决这类问题的关键。

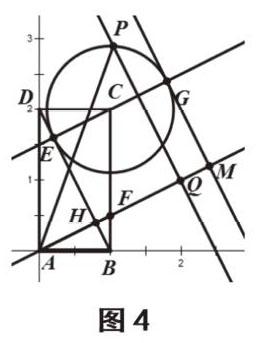
例4 （2017年全国Ⅲ卷 理科数学）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心，且与BD相切的圆上，若AP= λAB+μAD，则λ+μ的最大值为（    ）

应对策略：两种方法分别体现了向量与三角函数、参数方程和向量与解析几何的有机融合。向量既有代数特征又有几何特征，借助向量我们可以把某些代数问题转化为几何问题，也可以把某些几何问题转化为代数问题，突出数形结合的思想.这就要求我们要善于运用向量的平移、伸缩、合成、分解等变换，减少运算量，增加思维量，结合三角函数求值相关知识，求解最最值问题。

三、结语

综上所述，平面向量考点在高考中有易有难，掌握向量的基本概念及加、减法、数乘、数量积及坐标表示，利用数形结合的思想，利用化归的方法，综合运用三角函数、解析几何等知识，向量问题一定会在你手中迎刃而解。

【参考文献】

[1]刘绍学，章建跃.数学必修4[M].  北京： 人民教育出版社，2007.

[2]程旭升.  平面向量题型分析与复习策略[DB/OL]. http：//www.docin.com/p-19057437.html？docfrom=rrela，2020-6-14.