方程在几何题中的应用
叶少梅
【摘要】在数学教育活动中,大部分数学概念与教学知识之间存在着极为密切的联系,为优化教学活动,加深学生对于数学概念的理解,教师应努力尝试利用已经掌握的数学知识解决后续的数学问题,依靠既得的数学经验帮助学生解答数学学习问题。本文针对初中数学教学活动展开论述,思考方程在几何题教学活动中的应用。
【关键词】方程 几何题 应用
方程是基于西方數学理论发展而来的学习模块,通过对方程的计算、对未知数的选择,学生能够在较短的时间内明确掌握解题方向,并剔除其他信息对于教学活动的干扰,依靠方程,对客观学习问题做出回应。但在以往的教学活动中,方程多应用于抽象数字的计算当中,帮助学生利用方程解决几何问题,这是一次极具代表性的数学尝试。
一、推理证明,解决面积问题
方程从数学问题的数量关系入手,通过方程,教师能够帮助学生在所掌握的数学材料中提取新的可用知识,并根据数学问题的相关表述构建全新的数学模型,促使问题中已知的、未知的题干信息构成新的数量关系。在当前的初中数学教育活动中,方程的应用极为广泛,但大多以抽象数据的计算、数量关系的计算为核心任务,对于空间几何问题的影响并不明显,要将方程融合到几何问题当中,教师应明确把握方程问题与几何问题的相同点、共同点,依靠两种不同解题方式的相互辐射,重新定义数学解题活动。
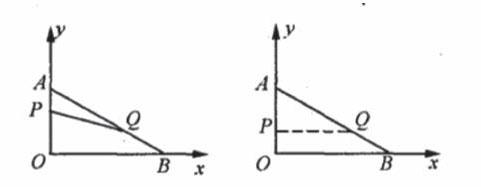
方程思想从问题的数量关系入手,几何问题则强调图形的位置关系、大小关系,其差别较为明显,利用方程解决几何问题,其教学实质等同于“数形转化”,基于这一观点,教师可将涉及到数字换算的数学问题提取出来,依靠方程建立新的数字关系,从而帮助学生解决几何问题。以初中数学教材《平行线及其判定》的相关学习为例,在这一板块的教学活动中,学生可能会接触到图形的折叠、变形,求面积问题,如图所示:
在这一几何结构中,图形的形状、边长、角度等性质在不断改变,直接求解的难度较大,教师可利用方程发起推理证明活动,帮助学生梳理图形之间的数量关系。在这一过程中,教师可帮助学生利用方程确定相关问题的数量关系,已知AD=8,AB=4,根据所给图形得出BE=x,则AE=8-x,BE=ED,进而列出解题方程式。在求解环节,学生能够利用等腰三角形的基本性质、平行线的基本概念等数学知识确定相应的数量关系,进而对方程进行求解,得出正确答案。与传统的解题方法相比,其所应用到的数学材料并不复杂,仅要求学生利用方程知识与已掌握的知识发起互动,对于学生来说,解题的开放性更强。
二、主观推测,解决思考问题
在初中阶段的几何教学活动中,部分教学问题在提问时并没有给出一个明确的思考目标,其要求学生计算最终的长度、面积,或对图形是否全等等内容进行判定,针对这类问题,其解题活动很容易受到学生主观意识的干扰,如果学生能够以积极的态度回应相关问题,向着“猜测”的方向不断靠拢,其所提出的答案的合理性也能够在一定程度上被保障。
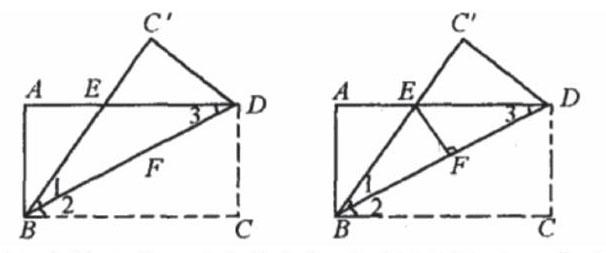
以初中数学教材《三角形全等的判定》的相关教学为例,针对该类问题,经常会出现以下类型的推导题:两个三角形放置在同一平面内,每个三角形上都有一个点,当两个点开始运动时,问何时两个三角形能够形成全等三角形?如下图所示:
这类问题中虽然给出了明确的数量关系,但如果只依靠学生的主观推导,计算的压力较大,且容易出现判断错误,教师可利用方程对该类开放性较强的问题做出回应,帮助学生更为积极的掌握解题方式。在解题活动中,教师可帮助学生确定两个三角形形成全等三角形的数量关系:(1)AC=BQ,AP=BP;(2)AC=PB,AP=BQ,在不同的全等关系下罗列对应的方程组,依靠数量关系得出最终答案。传统的教学方法要求学生独立对CP、QB、PB等边的长度进行计算,学生的运算压力较大,很容易出现计算错误,而在方程组的协助下,其能够直接摆脱无关变量对于问题的干扰,围绕问题的着力点建立方程式,进而对方程问题做出回应。
三、数形结合,确定数学关系
数形结合已经成为初中数学教学活动中的理想化方法,通过对数字材料的定向加工,教师能够依靠直观几何图形为学生创造观察与思考的对象,从而实现抽象问题的具体化处理,将复杂的数学问题转化为简单的数学结构。但对于初中数学教学活动来说,教学活动中所涉及到的相关知识以未知数的求值、位置关系的判定为主,在建立空间关系之后,几何图形可能会对原本的数量关系产生干扰,基于这一特点,教师可利用方程转化教学思路,帮助学生解决数学思考问题。
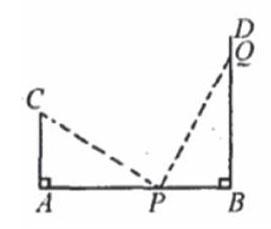
以初中数学教材《全等三角形》的相关学习为例,在这一板块的教学活动中,可能会涉及到位置关系推导问题、相似三角形推导问题,在这一板块,学生需要对角、边的数量关系进行整理,从而根据所得的大量数据进行运算,然后才能得出正确答案,如下图所示:
在问题中,Q是AB上不断运动的点,P是OA上运动的点,二者的运动速度不同,问到运动多长时间后,两个三角形成为相似三角形?在对这一问题进行解答时,教师可帮助学生围绕P的运动时间、Q的运动时间分别建立方程组,将对运动时间的求解转化为对未知数的求解,缩小学生的解题范围。通过导入时间t,利用二者的速度之差建立方程式,提高运算效率。在这一过程中,学生无需对客观图形进行推导,图形作为载体给出数据,在利用方程解题的过程中,解题速度大幅提升。
结语
方程在几何题中的应用越来越常见,在利用方程帮助学生解决几何问题时,教师应将几何概念与数字从问题中提取出来,依靠所给出的数学材料,重新确定数学关系,利用方程优化解题方法。
【参考文献】
[1]李国峰. 利用方程求解几何问题[J]. 数理天地:初中版, 2016, 000(004):P.31-32.
[2]海楠. 列方程解初中几何题举例[J]. 中学生数学:初中版, 2010, 000(012):P.17-18.
[3]杨燕. 中考中的几何、方程综合题[J]. 中学生数理化:初中版, 2003, 000(007):4-6.

