巧用平面直角坐标系解决几何问题
郭莉


【摘要】在初中阶段我们已经学习了平面直角坐标系,并利用平面直角坐标系,解决了许多平面的曲线问题。巧用坐标系,不仅降低运算难度,减少运算量,更是可以让我们解题思路明确清晰,有助解决问题。
【关键词】平面直角坐标系 几何
在初中几何问题中,恰当的运用平面直角坐标系可以把数量关系与直观的几何图形、位置关系结合起来,抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。本文结合近几年中考试题,谈一谈巧用坐标系解几何题。
点评:建立坐标系后将几何问题转化为函数解析式的代数问题,其中建系的方法不是唯一的,以点A,B,C,D为原点建立坐标系都可以。坐标系里的图形引入动点,与非坐标系里的图形引入动点研究的问题和解决的方法实质上是一样的,只是动点的刻画、问题的提出和结果表达,大都是以“坐标”相关的形式出发并落实的。因此可以这样说:坐标系里图形引入动点,就是在非坐标系里图形引入动点的基础上再融合“坐标法”的表示。本题是坐标系里图形变换的问题,解决的关键是将“变换”的特征与相应的点的坐标恰当地结合起来。
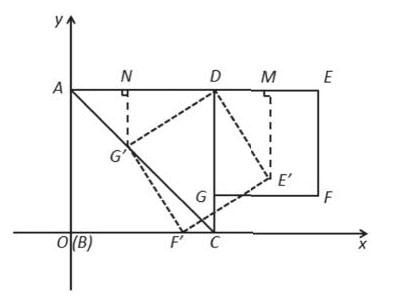
点评:本题考查旋转变换、正方形的性质、全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知識,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题,也可以建立坐标系采用坐标法求解。通过本题,可以再次体会到解析几何的一种基本思想方法就是建立坐标系,将几何问题通过代数计算的方法加以解决。此题若不通过建立坐标系,而是用纯平面几何的办法来解决,学生会感到无从下手,遇到的困难是添加辅助线。
平面直角坐标系架起了数与形之间的桥梁,可以使我们用几何的方法研究代数问题,又可以用代数的方法研究几何问题。数形结合思想可使复杂问题简单化、抽象问题具体化。

