一种新的绕组变形测试仪校准数据处理方法
吴 华,米思蓓,李 刚,陈习文,郭子娟,余宏明
(1.国网重庆市电力公司电力科学研究院,重庆 404100;2.中国电力科学研究院有限公司,湖北 武汉 430070;3.中国地质大学(武汉)工程学院,湖北 武汉 430074)
电力变压器是电力系统的重要设备之一,对电力运行安全起着至关重要的作用。变压器绕组发生局部变形后,必然会引起其内部参数的变化,通过对这些参数的测量和分析,就可以判断绕组是否存在变形,但传统方法通常难以对其内部参数进行全面检验。对于绕组变形测试仪的扫描频率精确度、检测精确度、选频滤波特性、阻抗匹配方式等关键技术指标,必须借助专用的衰减器来实现校准检测。但采用该衰减器对绕组变形测试仪进行实际检测中受很多不确定性因素的影响,其校准结果存在不确定度。针对校准结果存在的不确定度,实际操作中需要通过多次试验来减弱这种误差带来的影响。但在现有的试验条件下,通过多次试验需要花费大量的时间和精力[1]。本文基于二维非均匀插值算法甄别出校准结果中的不合理数据,并通过多次试验验证数据挑选的准确性和插值结果的合理性。
克里金插值是一种基于统计学变差模型的空间插值方法。该方法利用区域变量的原始数据和变异函数的结构特征估计未知点的属性值,是一种最优、线性、无偏估计方法。对于具有空间和时间相关性的插值数据,时空克里金插值算法可以用来较好地考虑时空数据的时空特征,从而获得更准确的插值结果。目前时空克里金插值算法已广泛运用于地质、气象、矿产资源、工程应用等多个领域[2]。如Pucci等[3]、Rouhani等[4]、Jaquet[5]、Bardossy等[6]、Nobre等[7]、Tarboton等[8]、Piotrowski等[9]研究了时空克里金算法在水文地质方面的应用;Bogaert[10]、Høst[11]、Lin等[12]将时空克里金算法应用于模拟数据;Kerwin等[13]将时空克里金算法应用于医学图像中估计心脏运动;Jost等[14]将物理确定性蒸发模型与时空地质统计插值相结合,用来预测土壤储水量;魏玉珍等[15]运用时空克里金插值算法对水库富营养化空间格局进行分析,并提出了防治对策;Gething等[16]将局部时空克里金算法应用于国家门诊疟疾数据集的插值;Liang等[17]将时空克里金插值算法应用于空气污染数据的非平稳时空结构中。时空克里金插值算法在普通克里金插值算法的基础上考虑了数据的时间特性,得到了更好的插值效果。
本文提出一种适用于变压器绕组变形测试仪校准装置校准数据的二维非均匀克里金插值算法。该方法首先基于校准数据的试验点在不同频率上的非均匀性,对每个频率上设置一个频率权重[ai],其中i代表不同频率的试验点,并针对校准数据的试验点在不同衰减量上的非均匀性,对不同衰减量设置一个衰减量权重[bj],其中j代表不同衰减量的试验点;然后针对绕组变形测试仪在不同频率下测得的衰减量显示值与标准值之间的差值作为插值对象构建二维变差函数模型,即每一个测试仪的校准数据,构建一个变差函数模型;最后通过优化算法寻得的权重值组合{[ai],[bj]}用来建立二维非均匀克里金差值算法,重构绕组变形校准数据的频率与衰减量的非均匀关系,以减弱校准装置校准误差对二维变差函数模型的影响。
1 基本算法
1.1 克里金插值算法
克里金插值的主要作用是估算空间未采样点的属性值[18]。假设存在某一研究区域D,区域化研究变量Y(x)为区域内X处的测量值,若区域内存在某一未采样点x,其估计值为Y*(x),则Y*(x)可以通过一个线性关系来估算:
(1)
式中:Y*(x)为x处的估计值;n为实际测量数量;Y(xi)为第i个位置处(xi)的实际测量值;αi为第i个位置处实际测量值的位置权重。
αi是一套使插值误差最小的最优系数,其需要满足如下无偏估计和估计方差最小两个条件:
(2)
根据拉格朗日乘数法对公式(2)进行简化,可得到:
(3)
式中:c(xi,xj)为Y(xi)和Y(xj)的协方差函数;c(x0,xj)为待插值点与已知样点之间的协方差;μ为拉格朗日乘子。
克里金插值算法的变差函数计算公式如下:
[i=1,2,…,n(h)]
(4)
式中:γ(h)为滞后距离h时对应的变差函数值;xi为第i个采样点;h为滞后距离;n(h)为滞后距离h时的样本点总数。
根据变差函数γ(h)与协方差函数之间的关系,通过变换上述方程组,可得到克里金方程矩阵如下:
(5)
通过克里金插值算法求取未采样点属性值时,需要先对已知采样点数据进行分析,求取试验变差函数值,再通过理论变差函数模型拟合离散的试验变差函数值,获得采样点数据的变差函数模型。即先根据公式(5)求取克里金插值中的权值,再将求解出的权值带入公式(1)中,求取未采样点的属性值。
1.2 粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)是一种通过信息共享,寻求到最优解的优化算法。该算法适用于非线性、非结构化解的寻优[19-21]。粒子的质量是用适应度函数来衡量的,它反映了解的最优性。所有潜在解的集合被称为解空间,一个潜在解被称为一个位置,记为Pos。没有质量、没有大小的粒子在解空间中以速度v运动,最优解是通过不断更新粒子的位置和速度得到的,而粒子在更新过程中朝个体最优位置Pib和群体最优位置Pgb移动。通过下式更新粒子的速度和位置:
vi+1=ω×vi+c1×Rand×(Pib-Posi)+c2×Rand×(Pgb-Posi)
(6)
Posi+1=Posi+vi+1
上式中:下标i表示PSO算法的迭代次数;Posi表示在第i次迭代中粒子当前的位置;vi表示在第i次迭代中粒子的速度;vi+1和Posi+1分别代表粒子更新后的速度和位置;Rand是一个(0,1)范围内的随机数;Pib表示粒子的个体最优位置;Pgb表示粒子的群体最优位置。
本文利用PSO算法首先将二维非均匀克里金插值中的衰减量权重和频率权重组合{[ai],[bj]}的维度作为解的维度;然后将插值结果的均方误差作为适应度函数;最后找到最优的权重组合能使得插值结果最好。
2 研究方法
本文提出的二维非均匀克里金插值方法给不同衰减量和不同频率赋予不同的权重值,并利用PSO算法对标准二维克里金算法进行重构,寻求适合于绕组变形测试仪校准装置校准数据特性的二维非均匀克里金插值算法,在不需要进行多次重复试验的情况下,减少了测量不确定度对试验结果的干扰。
2.1 二维克里金插值算法
二维克里金插值算法是一种基于样本空间统计相关的最优、线性和无偏估计量的内插方法。在常见的时空克里金插值中,考虑了空间和时间的相关性[22]。假设Z(s,t)是时空区域化变量,(s,t)表示时空域中的样本点位置。从空间域延展到时空域后的克里金模型如下:
(7)

(8)
二维克里金插值算法的变差函数方程如下:
(9)
式中:γ(rs,rt)为变差函数值;hs和ht为对应的样本之间在s和t两个不同维度的距离;Z(si,ti)为点i处的观测值;Z(si+hs,ti+ht)为与Z(si,ti)在第一维度上相距hs、第二维度上相距ht的点的观测值;n(hs,ht)是二维空间距离为hs和ht的样本点对的总数。
二维克里金插值中通过下式求解最小误差和无偏估计条件:
(10)
式中:γst表示二维可分离型变差函数。
二维克里金插值算法通过二维空间域的变差函数将不同的空间数据结合起来,通过增加普通克里金插值的维度提高了二维数据的插值效果。在实际应用中,不同维度的空间中变量的量纲不同,二维距离不能简单地运用各自维度的距离叠加来表示。而简单的二维克里金插值算法无法反映绕组变形测试仪校准装置校准数据的特性,因此本文提出了利用PSO算法构建二维非均匀克里金插值算法来解决此问题。
2.2 二维非均匀克里金插值算法
Z(x,f)是一个定义在非均匀二维空间域中的区域化变量,其中x表示样本点的衰减量位置坐标,f表示频率域中的位置点。如果采样点的数量为n,则二维非均匀域中的克里金模型定义如下:
(11)
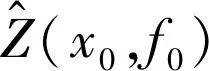
在非均匀二维域中,变差函数值的大小与两点之间的二维空间距离密切相关,定义非均匀二维变差函数的计算公式为
(12)
式中:pf表示非均匀二维空间域中的一个样本点;h表示两个样本点之间的距离;γpf(h)为变差函数值。
非均匀二维变形场模型给出的最优距离求解方法可以有效地用于测量非均匀二维空间域中的两个样本点之间的距离h。最优距离方案表示如下:
(13)
式中:[ai]和[bj]为POS算法寻求的最优权重系数;Sij为样本点的二维数据(其中,i表示选取的频率点,本文中i=1,2,3,4;j表示不同衰减量,j=1,2,3,…,9)。
在求得两个样本点之间的距离h和变差函数值γpf后,使用h和γpf进行理论变差函数模型的拟合。根据理论变差函数模型和待插值点与已知点之间的二维空间距离,即可求得对应的变差函数值,并将其用于克里金方程组的求解。在非均匀二维空间域中其求解的公式如下:
(14)
二维非均匀克里金插值的一组权重系数λi可以通过求解方程得到,该组权重系数是一套使插值误差最小的最优系数,其维度与研究区域中已知点的个数相同。将λi代入二维非均匀域中的克里金模型定义中,即可得到待插值点的属性值。
3 案例分析
3.1 模型构建
本文选取型号为RZB-1的变压器绕组变形测试仪校准装置,在温湿度适宜的情况下,使用二维非均匀克里金插值算法针对多个绕组变形测试仪校准装置的基本校准数据的误差数据进行插值。原始的校准数据是在测试仪器设备4个频率段(1 kHz、10 kHz、100 kHz、300 kHz)和9个衰减量(-1.21 dB、-2.02 dB、-4.30 dB、-6.12 dB、-9.90 dB、-20.03 dB、-29.82 dB、-40.30 dB、-49.85 dB)进行采集的,本文选取该校准装置对7台设备的校准数据值作为训练样本,构建二维非均匀克里金插值模型,选取4台设备的校准数据值作为测试样本,检验该模型的有效性。衰减量的数值与校准误差不在一个数量级上,如果将原始的校准数据作为插值对象,难以反映校准误差。因此,本文选用衰减量显示值(dB)与标准值(dB)之间的差值作为插值对象,将差值构成的二维数据Sij作为非均匀二维域中的区域化变量。综合考虑研究对象的二维特性,将曲线的幅值数据构建为二维变形场模型,如下式:
mod=(aibjSij) (i=1,2,3,4;j=1,2,…,9)
(15)
其中,下标i表示不同的频率;下标j表示不同的衰减量。
选择7个校准样本数据作为试验数据,运用POS算法对校准数据进行参数寻优,将二维非均匀克里金插值交叉验证结果的均方误差作为适应度函数。POS算法按照经验设置初始参数学习因子c1、c2均为1.5,惯性权重w为0.729 8,初始化种群大小为20。
首先在0.95~1.05的范围内初始化种群个体位置,粒子的维度为13,将解空间的范围设置在[0.50,2.00],解的精度设置为0.01,如下式:
particle1=[a1,a2,a3,a4,b1,b2,b3,b4,b5,b6,b7,b8,b9]
(16)
当适应度函数收敛或者迭代次数超出规定次数后终止。然后通过POS算法得到二维非均匀克里金插值模型的13维权重最优解为[1.10,1.07,1.06,0.94,0.90,0.67,0.52,0.85,0.95,0.95,0.90,0.94,0.90]。
最后使用上述13维权重构建插值数据,并完成二维变差函数的调整,如下式:
(17)
其中,每一列为同一衰减量不同频率点、每一行为同一频率不同衰减量的二维非均匀克里金插值调整后的数据。
为了验证该处理方法的有效性,本文针对数据点a3b9S39重复做了10次试验,其试验结果见图1。在图1中,对这7个校准数据的10个试验数值的最大值、最小值、平均值进行了对比研究,并画出试验中所用的数值(即试验用值)和运用二维非均匀克里金插值计算结果的连线。
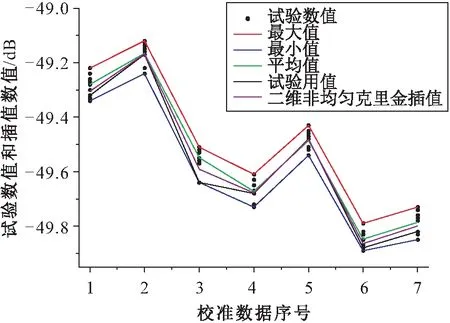
图1 数据点a3b9S39的10次试验结果Fig.1 10 test results of data point a3b9S39
由图1可见,通过本文处理方法插值出来的数据更接近多次校准数据的平均值,比起试验用值来说更少地选用靠近极值的数据。
3.2 插值结果
本文使用二维非均匀克里金插值算法对变压器绕组变形测试仪校准装置的基本校准数据的误差数据进行插值。首先将{[ai],[bj]}系数值乘以对应校准数据与衰减量的差值,利用二维非均匀变差函数计算各个点的变差函数值,得到变差函数模型;然后计算待插值点和所有已知样本点之间的距离并代入变差函数模型中得到对应的变差函数值;最后求解算法的方程组得到一组权重系数,将权重系数和已知样本点的差值进行加权调整后,运用二维非均匀克里金插值方法对所有数据进行遍历插值,即可得到数据的修正值,再将该数据加上衰减量,就成为调整后的最终数据了。数据点S394次校准数据与衰减量差值的插值结果见图2,数据点S394次校准数据的多次试验结果与二维非均匀克里金插值结果对比见图3。

图2 数据点S394次校准数据与衰减量差值的插值 结果Fig.2 Interpolation results of the difference between four different calibration data and attenuation magnitude of the data point S39
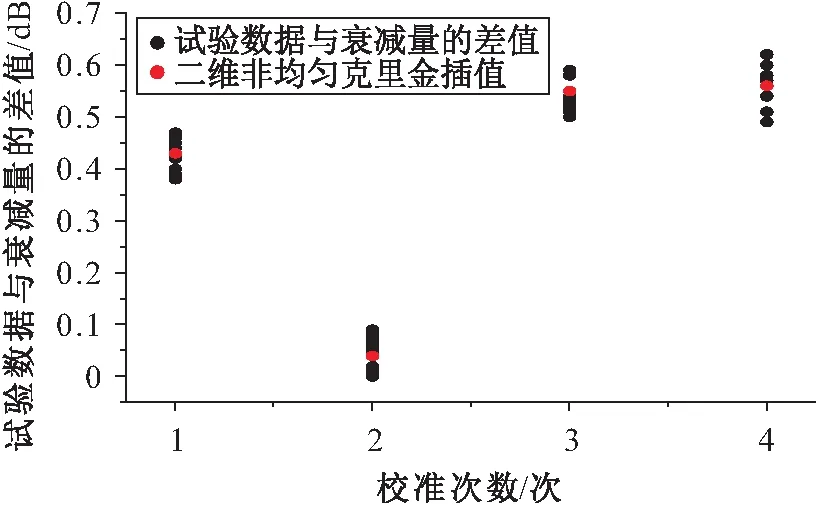
图3 数据点S394次校准数据的多次试验结果与二维 非均匀克里金插值结果对比图Fig.3 Comparison diagram of four calibration data of data point S39 between multiple tests and two- dimensional non-uniform Kriging interpolation
由图2和图3对比可知,对数据点S39在第一台测试设备上,多次重复试验的试验数据与衰减量的差值在0.38 dB~0.47 dB之间,由校准结果分散性引入的不确定度分量为0.04 dB,而经过二维非均匀克里金插值后的数据差值为0.43 dB,与多次校准数据的平均值仅仅相差0.01 dB,大大地弱化了因为校准结果分散性而造成的不确定度;后面3台设备的结果也同样证明了该方法的有效性。因此,二维非均匀克里金插值方法应用于变压器绕组变形测试仪校准装置校准数据的处理中,能有效地降低因为校准结果分散性而造成的不确定度,提高校准的精度。
4 结 论
本文提出了一种基于二维非均匀插值算法的变压器绕组变形测试仪校准数据处理方法。对同一种计量标准,通过对不同的多台测试仪器的校准结果进行了二维非均匀插值处理,利用该方法提取了与计量标准相关的特征,并运用该特征对后面校准结果进行了调整与校准。试验证明:该方法有效地降低了校准结果分散性而引入的不确定度,与直接校准相比,无需花费大量时间进行多次试验来减少误差,提高了绕组变形测试仪校准数据质量和校准精度,对测试仪的校准评价更为准确,保障了电网的安全运行,具有很好的社会效益和经济效益。

