利用多孔抽水试验确定承压-无压流条件下承压含水层的水文地质参数
李 丞,王宁涛,胡 成,常 威1,,孙 伟1,,黄 琨
(1.中国地质大学(武汉)研究生院,湖北 武汉 430074;2.中国地质大学(武汉)环境学院,湖北 武汉 430074;3.中国地质调查局武汉地质调查中心(中南地质科技创新中心),湖北 武汉 430205)
确定含水层的渗透系数K、给水度μ等水文地质参数是开展地下水资源量评价的基础[1-2]。抽水试验是确定松散岩类孔隙含水层水文地质参数最常用的技术方法[3-5]。根据抽水试验获取的含水层水位随时间的变化曲线,并结合水文地质条件选择相应的井流模型即可求取含水层的水文地质参数。对于承压含水层,常用的求参方法有基于泰斯(Theis)承压井流模型的Jacob直线图解法、标准曲线配线法[6-7]。对于潜水含水层,常用的井流模型包括泰斯潜水井流模型、考虑含水层滞后给水的博尔顿(Boulton)模型以及考虑弹性释水的纽曼(Neuman)模型[8-10]。在承压含水层中,当抽水井持续抽水引起地下水水位降至隔水顶板以下时,抽水井中地下水由承压状态往无压状态转化,出现承压-无压流并存的现象。而针对承压含水层中承压-无压状态并存条件下的井流模型有Moench承压-无压井流模型和Chen承压-无压井流模型[11-13]。
1 研究区概况
研究区位于江汉平原北部肖家港地区,该地区地势平坦,整体表现为北高南低、东西高中间低,澴河两侧往河床微微倾斜。研究区内地表大部分面积为第四系所覆盖,区内仅在北部、东北部地势相对较高处出露少量青白口系武当群(Qbw)变质岩、震旦系(Z)硅质岩以及古近系(Ey)砂岩、砂砾岩,见图1。
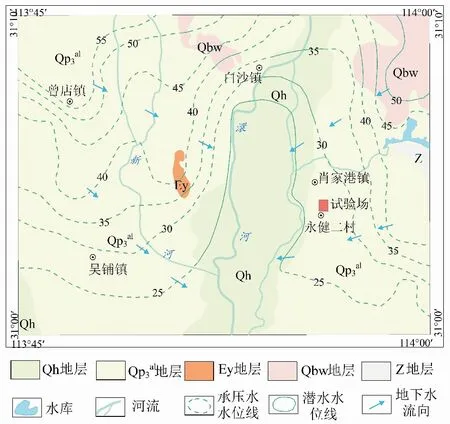
图1 研究区水文地质图Fig.1 Hydrogeological map of the study area

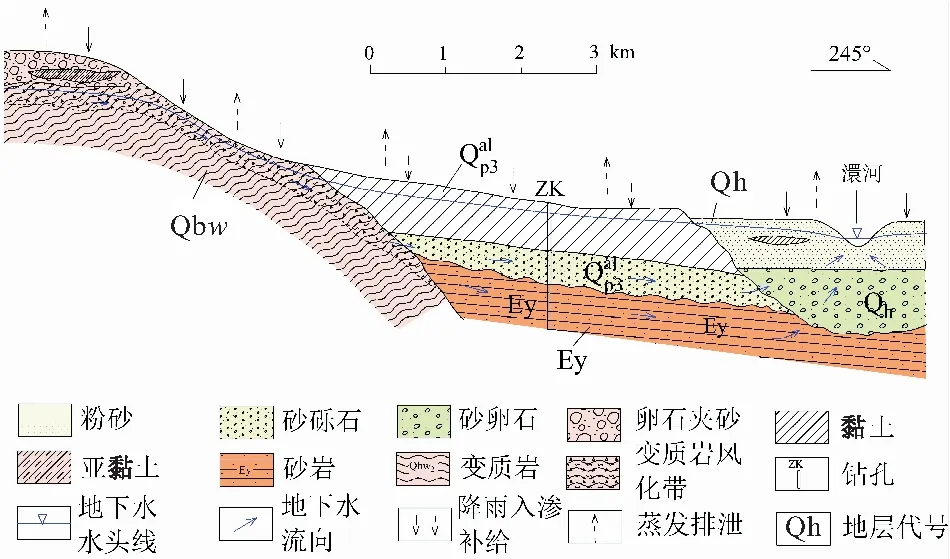
图2 研究区地下水补径排特征示意图Fig.2 Schematic diagram of groundwater recharge and discharge in the study area
2 多孔抽水试验


图3 研究区水文地质钻孔平面位置分布Fig.3 Plan distribution of hydrogeological boreholes in the study area
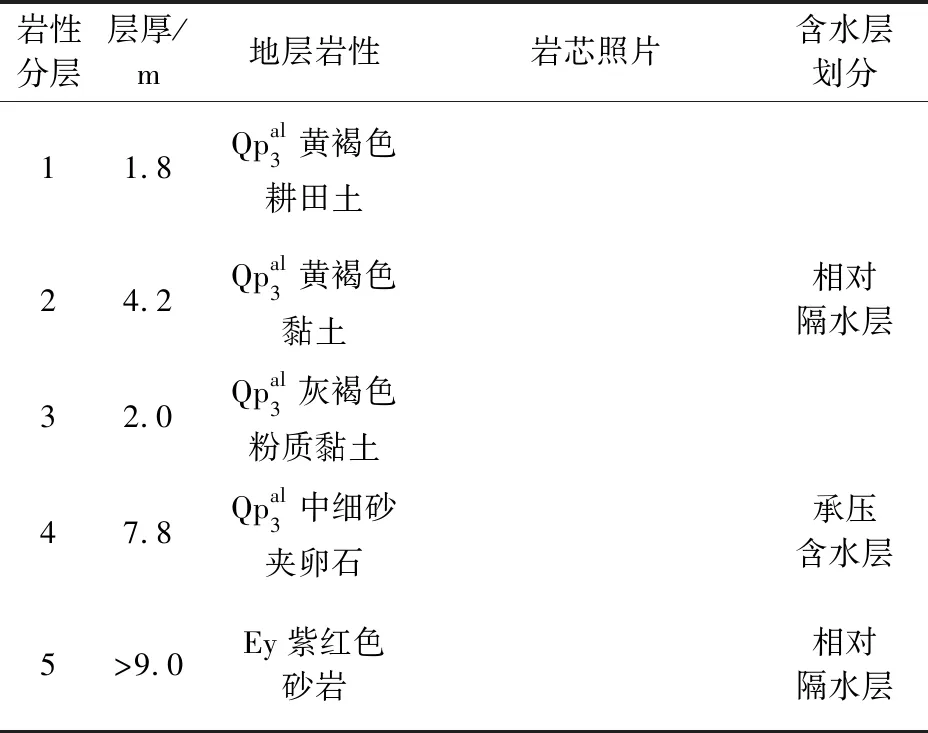
表1 研究区岩性及含水层划分Table 1 Lithology and aquifer division of the hydrogeo-logical boreholes in the study area
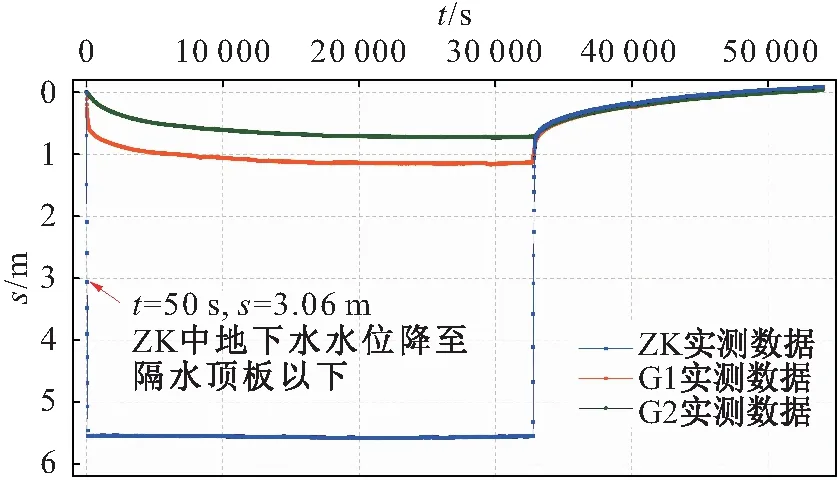
图4 抽水井ZK和观测井G1、G2中地下水水位降 深(s)-时间(t)曲线Fig.4 Drawdown-time curves of pumping well ZK and observation wells G1 and G2
由图4可见,抽水井ZK和观测井G1、G2中地下水水位的最大降深分别为5.57 m、1.14 m、0.72 m,其中抽水井ZK中地下水水位在抽水进行50 s时已降低至隔水顶板以下而转换为无压状态,而观测井G1、G2中地下水水位在整个抽水过程中均高于隔水顶板,保持在承压状态,即本次多孔抽水试验过程中出现了无压-承压流并存的现象,并且试验过程中相较于承压含水层整体降落漏斗的影响范围很小,可以概化为无限含水层。
3 承压含水层水文地质参数的求解及分析
3.1 泰斯承压井流模型的直线图解法
对于本次多孔抽水试验,首先利用泰斯承压井流模型的直线图解法求解承压含水层的水文地质参数,并分析承压含水层抽水井附近无压区的出现对参数求解的影响。
在满足泰斯假定条件下,承压含水层空间上任意点的地下水水位降深为
(1)
式中:s为观测井中地下水水位降深(L);Q为抽水流量(L3/T);W(u)为u的井函数,u=r2μe/4Tt[其中,T为含水层导水系数(L2/T);μe为含水层弹性释水系数;r为观测井到抽水井的距离(L);t为计算地下水水位降深的时刻(T)]。

(2)
对于确定的含水层和观测井,公式(2)中T、μe、Q、r均为常数,故s与lgt呈直线关系,此直线斜率m为
(3)
此直线与lgt轴的交点t0为
(4)
本文绘制了观测井G1、G2的实测s-lgt曲线,见图5。

图5 泰斯承压井流模型的直线图解法求解承压 含水层水文地质参数的示意图Fig.5 Diagram of hydrogeological parameters estimation of the confind aquifer with Cooper-Jacob method of Theis model
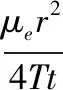
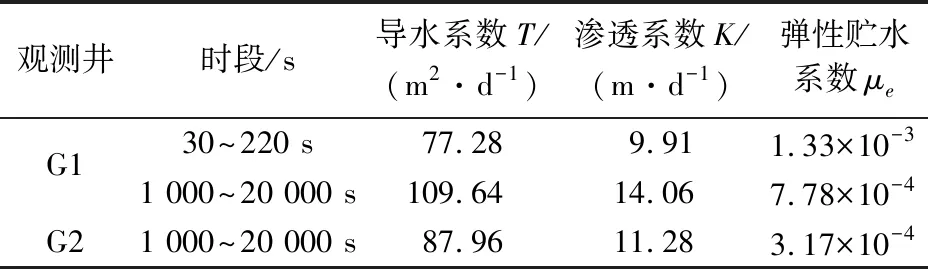
表2 泰斯承压井流模型的直线图解法求解承压含水层水文地质参数结果Table 2 Hydrogeological parameter estimation of the confind aquifer with Cooper-Jacob method of Theis model
由表2可知,利用泰斯承压井流模型的直线图解法处理观测井G1、G2的地下水水位降深变化数据所求得的承压含水层导水系数T值的变化幅度较小,在77.28~109.64 m2/d之间,而所求得的承压含水层弹性释水系数μe值的变化幅度较大,在3.17×10-4~1.33×10-3之间。其中,利用观测井G1第二直线段与观测井G2直线段求取的承压含水层水文地质参数值比较接近,而与观测井G1第一直线段的求参结果差异较大。为了评价求参结果的准确性,分别将计算得到的承压含水层水文地质参数代入公式(2)中反求观测井G1、G2中地下水水位的理论降深值,并与实测降深值进行了对比,见图6。
由图6可见,根据观测井G1第一直线段所得参数计算得到的理论降深值与观测井G1、G2的实测降深值均相差较大[图6(a)、(d)];根据观测井G1第二直线段所得参数计算得到的理论降深值与观测井G1的实测降深值较吻合[见图6(b)],但与观测井G2的实测降深值相比则明显偏低[见图6(e)];根据观测井G2所得参数计算得到观测井G2的理论降深值与其实测降深值较为一致[见图6(f)],但观测井G1的理论降深值与其实际降深值相比则偏高[见图6(c)]。根据试验场条件及抽水试验数据可知,含水层承压高度为2.72 m,当抽水持续仅50 s后抽水井的地下水水位降深已达3.06 m,利用阿勃拉莫夫公式计算此时水跃值[14],可得此时抽水井井壁处地下水水位降深为2.98 m,即承压含水层抽水井附近一定范围内地下水水力特征由承压转换为无压(见图7),因此抽水初期含水层的释水量由抽水影响范围内承压含水层的弹性释水和无压区的重力释水共同提供。但由于承压含水层的重力给水度μd远大于弹性释水系数μe,在抽水初期地下水水位降落漏斗的范围较小,无压区含水层的重力释水量所占比例较大不可忽略,故此时求解的承压含水层的给水度值是介于重力给水度与弹性释水系数之间的综合值;同时,由于承压含水层的重力释水具有滞后性,其地下水水位变化响应速度小于纯承压含水状态的压力传导,导致抽水引起的观测井中地下水水位变动初始响应时间t0偏大,由公式(4)可知,这将导致所求承压含水层的弹性释水系数值偏大。随着抽水时间的持续,地下水水位降落漏斗的整体范围不断扩大,无压区的扩展速度逐渐变慢并趋于稳定,承压含水层重力释水的影响减弱,承压含水层的弹性释水量逐渐占据主导地位,因此利用观测井G1初期数据,即s-lgt曲线第一直线段的数据求参结果具有明显误差,尤其是μe的计算值明显偏大,而利用观测井G1中后期数据,即s-lgt曲线第二直线段的数据求参结果则比较接近实际。对于观测井G2,由于其距离抽水井ZK的距离较远,如图7所示,当抽水引起的地下水水位变动影响到观测井G2处时,承压含水层抽水井附近的无压区范围已经基本稳定,此时含水层无压区重力释水量相较于弹性释水量几乎可以忽略,对观测井G2中地下水水位降深的变化几乎没有影响,同时对观测井G2中地下水水位变动初始响应时间t0的影响也相对较小,因此利用观测井G2的观测数据计算承压含水层的水文地质参数基本满足泰斯承压井流模型的假定条件,其s-lgt曲线也只有一段直线段,求参结果也更符合实际水文地质条件。

图7 承压含水层地下水释水示意图Fig.7 Schematic diagram showing the change in groundwater storage of confined aquifer
为了进一步分析抽水井附近地下水发生承压-无压转换对地下水水位降深-时间曲线的影响以及泰斯承压井流模型在承压-无压问题上的适用性,绘制了观测井G1、G2的地下水水位降深-时间特征曲线图并与标准特征曲线进行了对比(见图8),特征曲线表示地下水水位降深随时间的变化速率。
由图8可见,观测井G1的地下水水位变化特征与双重含水介质或者非承压含水系统相似[15-16],在抽水过程中地下水水位降深随时间的变化速率变小而呈现下凹形态,这表明承压含水层重力释水产生的延迟作用,即由于承压-无压转换而存在一个过渡期,该时期内承压含水层无压区重力释水的增量降低了承压区弹性释水的速度,从而导致地下水水位下降速度变缓,这也对应着图5中观测井G1的s-lgt曲线两直线段中间的过渡部分;与观测井G1不同,观测井G2的地下水水位变化特征图并未出现下凹段,整体上基本符合承压含水系统的地下水水位变化特征,说明当观测井距离抽水井较远时,承压含水层抽水井附近小范围无压区的出现对地下水水位变化特征的影响较小,利用泰斯承压井流模型进行承压含水层水文地质参数求解具有一定的可靠性。

图8 观测井G1、G2地下水水位降深-时间特征曲线图Fig.8 Diagnostic diagram of the time-drawdown curve of observation wells G1 and G2
3.2 Chen承压-无压井流模型
陈崇希教授基于吉林斯基势函数,将含水层的导水系数和给水度分时段视为空间上的平均值Tm和μm,并近似地视为常量,在含水层的导水系数T、弹性释水系数μe和重力给水度μd已知的情况下,建立了流量、抽水井地下水水位及对应的降落漏斗曲线与时间之间的函数关系,即Chen承压-无压井流模型。Chen模型中地下水承压-无压井流问题可描述如下:
(5)
(6)
式中:h、H分别为无压区水位和承压区的水头(L);H0为初始水头(L);R为承压转无压流的径向距离(L),即承压-无压转换半径(L)。
将h=M和r=R代入公式(6),可得承压-无压转换半径为
(7)
依据水均衡原理,抽水量的总体积等于承压含水层内部承压区的弹性释水量和无压区的疏干排水量之和(见图7),据此建立承压含水层水均衡方程如下:
Qt=μeVe+μdVd
(8)
其中,承压含水层承压区弹性释水体积Ve为

(9)
承压含水层无压区重力疏干排水体积Vd为

(10)
式中:rw为抽水井半径(L)。
根据Chen模型的基本原理可知,当已知承压含水层的导水系数T和弹性释水系数μe时,根据承压-无压抽水试验的地下水水位降深变化数据可以进一步确定承压含水层的重力给水度μd。具体方法如下:首先将观测井G2的地下水水位降深-时间数据(t=1 000~20 000 s)求得的含水层导水系数T和弹性释水系数μe作为含水层真实的导水系数和弹性释水系数,同时以在t=20 000 s时求得的含水层导水系数和给水度作为空间上的平均值,即取Tm=87.96 m2/d、μm=3.17×10-4,将该组参数代入公式(7)求取t=20 000 s时的承压-无压转换半径R;然后将R代入公式(9)、(10)分别获得承压含水层承压区弹性释水体积Ve和无压区重力疏干排水体积Vd;最后将抽水流量Q、抽水时间t、含水层弹性释水系数μe以及Ve、Vd代入公式(8),最终求得承压含水层重力给水度μd值为0.197,处于《水文地质手册》(第2版)中细砂-砂砾石的重力给水度经验值0.15~0.35范围之间,说明该结果比较合理[18]。
4 结 论

(2) 泰斯承压井流模型在一定条件下仍能用于承压-无压井流问题并求解承压含水层的水文地质参数,虽然由于承压-无压的转换会引起承压含水层释水机理、流场变化特征发生改变,不满足泰斯承压井流模型的假定条件,导致其所求的承压含水层弹性释水系数偏大,但是可以通过选取抽水后期或者距离抽水井较远的观测井地下水水位降深数据,以尽量降低承压-无压转换的影响,并得到较为可靠的承压含水层水文地质参数值。

