基于DE-MELM的土质边坡稳定性预测方法
陈 茸,韩宝安,韩宝华,甘旭升
(1.四川交通职业技术学院建筑工程系,四川 成都 611130;2.四川交通职业技术学院信息工程系,四川 成都 611130;3.空军工程大学空管领航学院,陕西 西安 710051)
人工或天然土质边坡常常因人为因素或自然因素破坏其力学平衡,发生滑坡等现象,导致严重事故,不仅会造成生命和财产损失,还会对生态环境等造成巨大破坏。因此,土质边坡稳定性研究具有重要意义,也受到了广泛关注。滑坡发生的过程实际上是斜坡从渐变性发展到突发宏观滑移的非线性复杂过程,由于土质边坡土体的结构与物理力学性质表现出宏观和微观上的不连续性和高度的非线性等特点,所以土质边坡工程可以看成是不确定的、非线性的、动态开放的复杂大系统,其稳定性受地质因素和工程因素等的综合影响。这些因素大部分具有模糊性、随机性、可变性等不确定性特点,它们对不同类型边坡土体稳定性的影响程度也是变化的,且这些因素之间具有复杂的非线性关系。不难理解,土质边坡稳定性问题是一个典型的非线性问题,很难用解析的数学公式来刻画,对其稳定性做出准确预测是岩土工程领域亟待解决的科学难题。
以往研究边坡稳定性预测问题,多采用瑞典圆弧法[1]、泰勒图表法[2]、有限元法[3]等方法,这些方法主要从分析土质边坡稳定性的影响因素出发来解决问题,但存在计算量过大、过程繁冗等不足,要准确刻画影响因素之间这种复杂的非线性特征尚存在一定的困难。随着神经网络等人工智能方法的广泛应用,其为土质边坡稳定性预测问题提供了一种新的解决途径[4-5],该方法无需剖析系统内部的关系,通过“黑箱”建模思想刻画样本数据中的内在特性及规律性,克服了传统有限元分析等方法的缺陷,但由于理论根基导致的泛化性能不高、局部收敛等问题,使其应用推广受到一定的限制。极限学习机 (Extreme Learning Machine,ELM) 是一种从前馈神经网络基础上发展起来的机器学习方法,不同于传统学习方法,它随机选择隐含层节点,以解析计算的方式确定输出层权值,理论上能以较快的速度获得较好的泛化性能[6]。但是,ELM也存在一定的局限性,如对样本中存在的粗差干扰抵御性较差,建模过程中随机确定隐含层输入权值和偏差导致预测误差较大。基于此,本文提出一种能够抗粗差干扰的土质边坡稳定性ELM预测方法,并引入差分进化 (Differential Evolution,DE) 算法优化隐含层输入权值和偏差,进而通过实例仿真验证了所提方法的有效性和可行性。
1 改进的极限学习机
1.1 标准极限学习机
极限学习机(ELM)是一种单隐层前馈神经网络(Single-hidden Layer Freedforward Network,SLFN),其通过随机方式生成隐含层输入权值和偏差,并兼顾识别准确率以及算法拓展性之间的平衡[7-8],目前已被广泛应用于各个领域。
对于N维训练样本{xj,ti},且xj=[xi1,xi2,…,xin]T∈Rn和ti=[ti1,ti2,…,tim]T∈Rm,则SLFN输出表示为
(1)
式中:L为隐含层节点个数;wi为输入节点和隐含层节点的连接权值向量;g(x)表示隐含层激励函数;βi=[βi1,βi2,…,βim]T为隐含层节点i与输出节点的输出权值向量;bi为第i个隐含层节点的偏置值;wi·xj表示wi与xj的内积。
公式(1)的矩阵形式为
Hβ=T
(2)
其中:
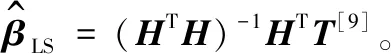
若公式 (2) 中加入误差V,则有:

(3)
不难得到误差方程为

(4)
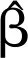
(5)
当P为单位矩阵时,公式(5)与最小二乘估计的形式相同。
1.2 MELM算法
M估计是从最小二乘估计发展起来的一种抗差估计方法[10],其遵循的基本准则为
(6)
考虑到Vi是未知参数的函数,对公式 (6) 关于参数X求导,并使之为零,以便计算极值,并将公式 (4) 代入,整理得到:
(7)
其中,权函数P(Vi)=ρ′(Vi)/V,且P(Vi)=diag[P1(Vi),P2(Vi),…,Pn(Vi)]。
则可得到在M估计下ELM的输出权值矩阵为
(8)

MELM权函数P(Vi)的选取采用如下的一次范数最小法[10]:
(9)
其中,K为一比较小的量。
对于训练样本(xi,ti),xi=[xi1,xi2,…,xin]T∈Rn,ti=[ti1,ti2,…,tim]T∈Rm,激励函数为g(x),隐含层节点为L(L≤N),则MELM算法的实现步骤如下:
(1) 取输入权值ai与隐含层节点的偏差bi为[-1,1]内随机数;
(2) 通过给g(x)构造矩阵H;

(4) 利用P(Vi)为各观测量初始赋权;
2 差分进化(DE)算法
差分进化(DE)算法的基本原理是:首先在种群中随机选取或按照一定策略选取3个个体,将其中两个个体的差分向量进行线性尺度变换;然后与第三个个体叠加以获得新个体;最后利用目标函数对新个体与种群中预先选定个体进行评价,保留较优个体[11-12]。对于函数最小化问题:
minf(x),x=[x1,x2,…,xd]
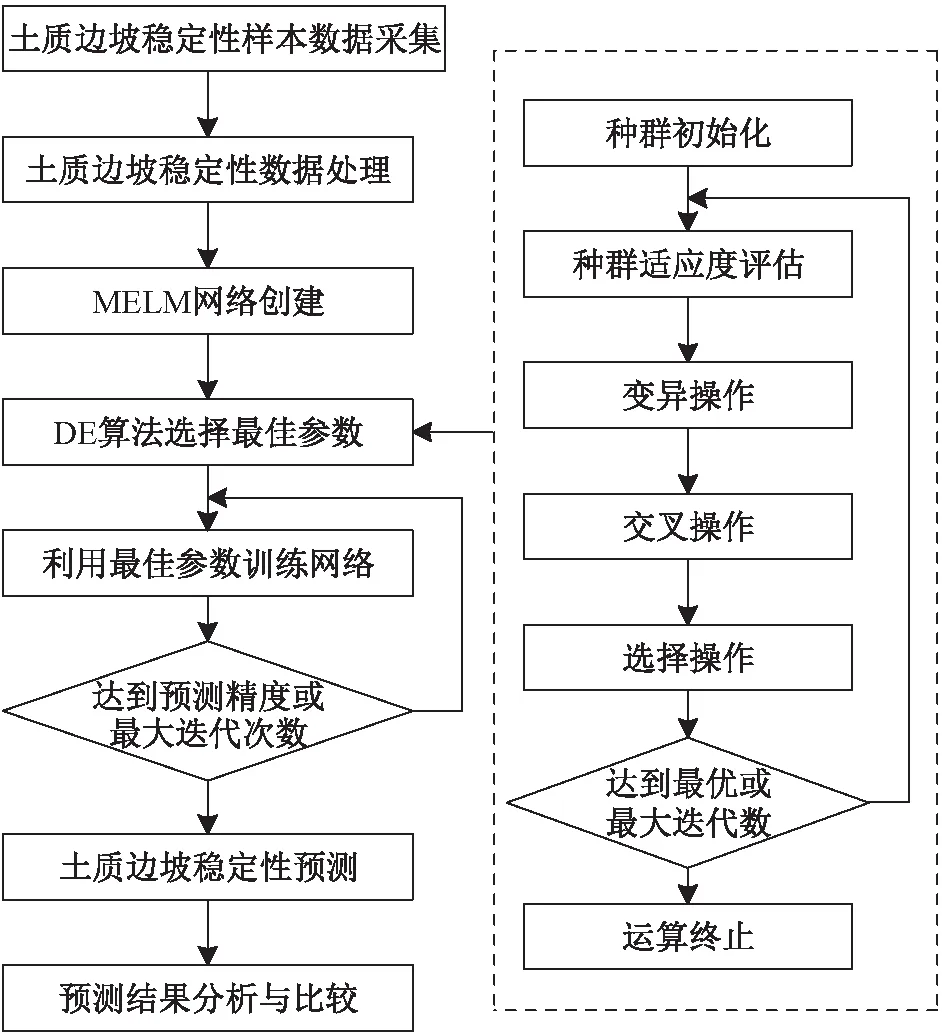
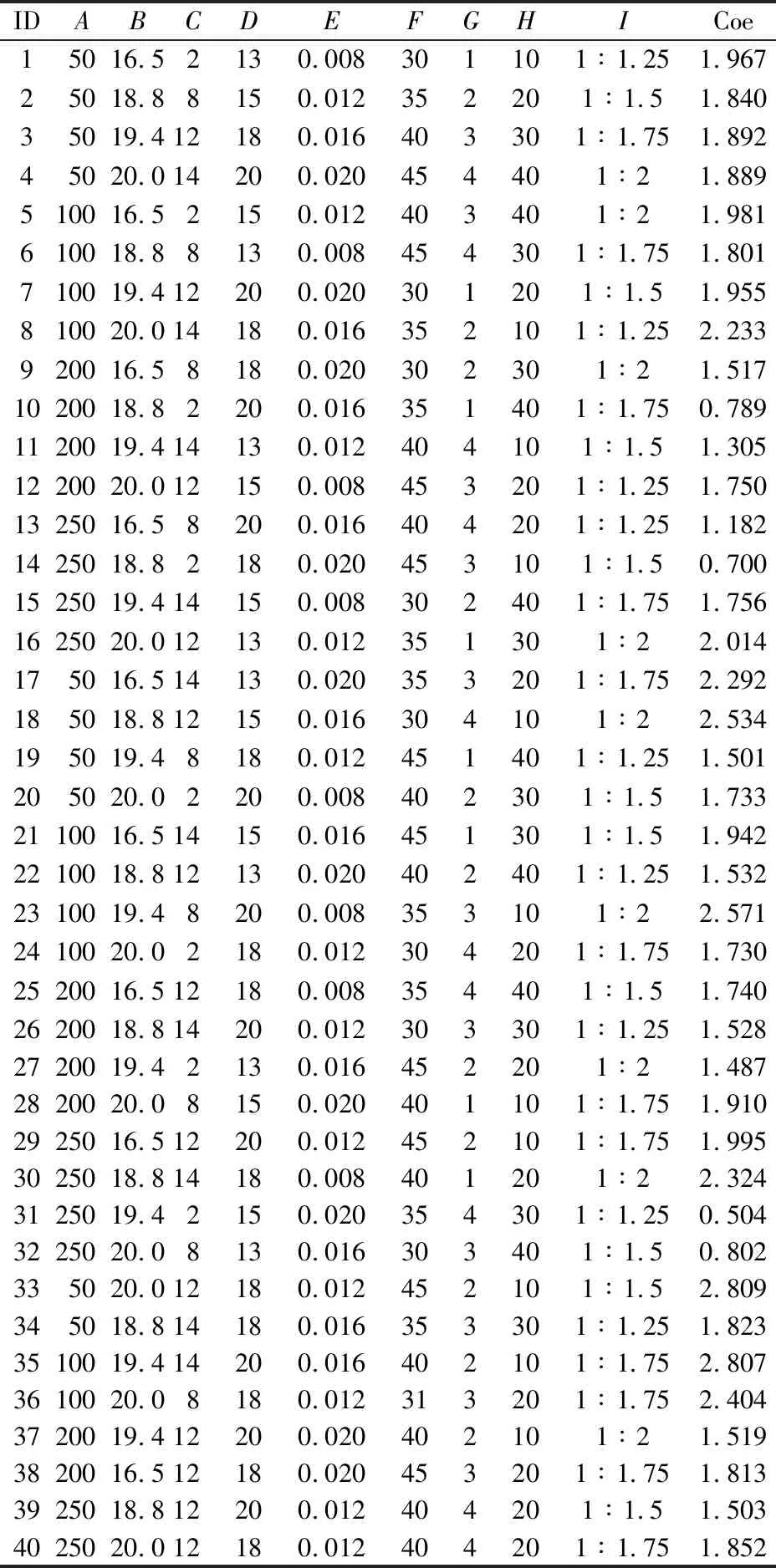
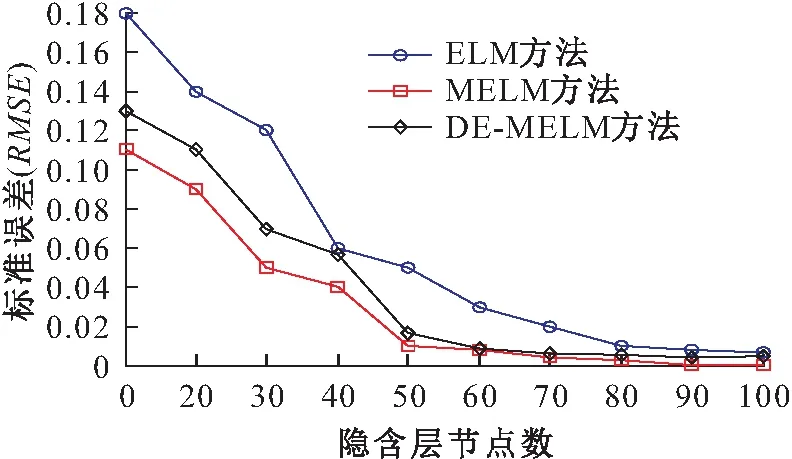
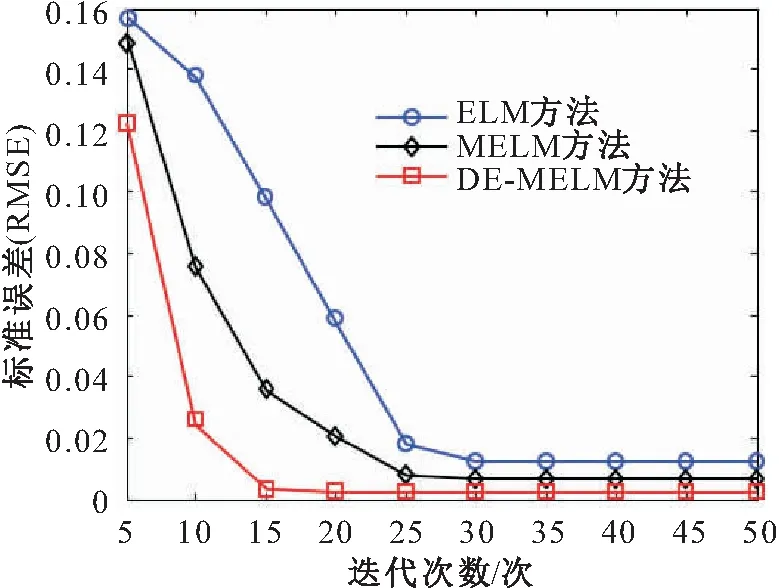
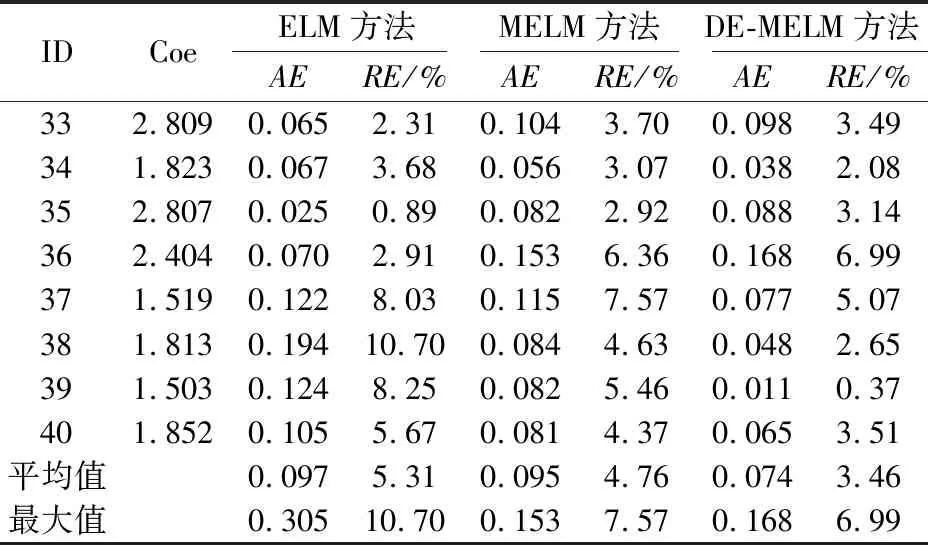
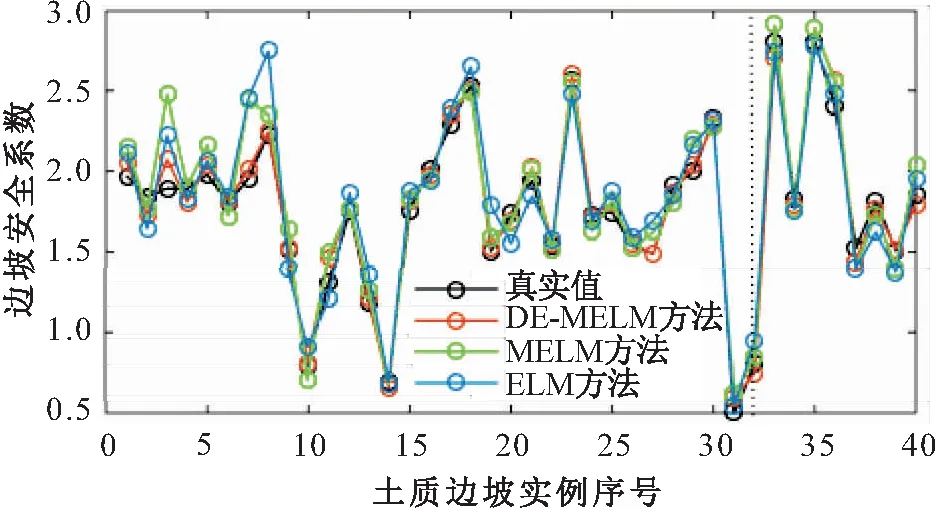
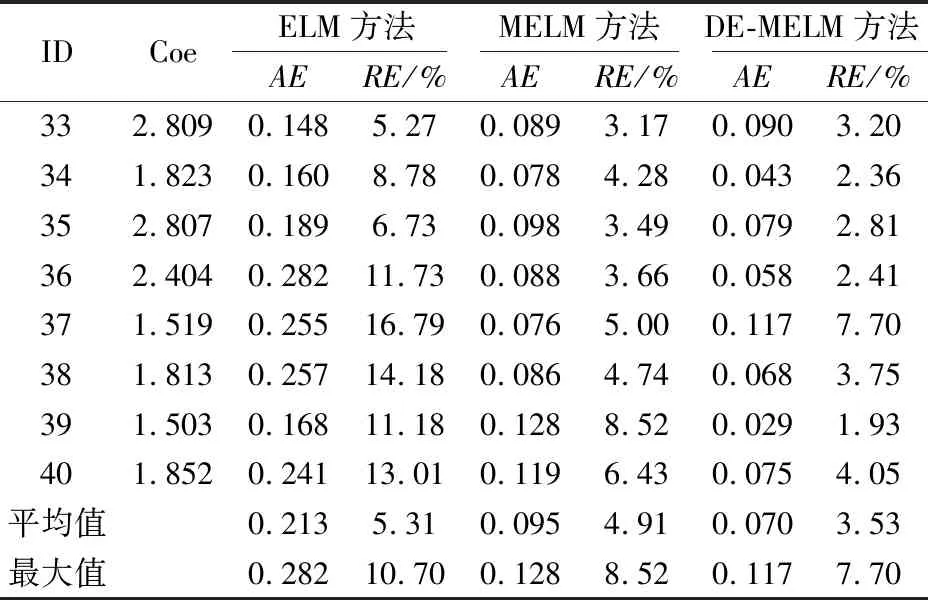
lk (10) 式中:xk为第k维变量;lk为第k维变量的搜索下界;uk为第k维变量的搜索上界;d为问题维数。 初始化参数,令xi=[xi,1,xi,2,…,xi,d]为种群中个体i对应的解。随机产生包括NP个个体的种群: xi,k(0)=lk+Rand·(uk-lk) (k=1,2,…,d;i=1,2,…,NP) (11) 式中:Rand为区间[0,1]内均匀分布的随机数。 DE算法包括变异操作、交叉操作和选择操作,现做逐一介绍。 在第g代进化中,选取当前种群个体xi(g),通过差分变异操作生成目标个体ti(g)。在诸多变异策略中[13],本文选取的变异策略为DE/Rand/1(其中,Rand表示变异操作的基为当前种群中随机选取一个个体;1表示线性尺度变换的差分向量个数),其过程描述为 ti(g)=xr1(g)+F·[xr2(g)-xr3(g)] (12) 式中:r1,r2,r3为从[1,N]中随机选取的异于下标i且相互独立的整数;F∈(0,1),为缩放差分向量的比例因子。 二维函数优化中DE/Rand/1变异策略产生变异向量的过程,见图1。 图1 二维参数空间中“DE/Rand/1”变异策略Fig.1 “DE/Rand/1” mutation strategy in two- dimensional parameter space 为了改善种群多样性,需对目标个体进行交叉操作。通过将目标个体ti的部分变量替换为当前种群中个体xi中对应位置的变量,获得测试个体vi。由此可以看出,交叉操作能将个体中的优良变量保留至下一代,增强了DE算法的局部搜索能力[14]。本文只介绍DE算法中常用的二项交叉操作。 二项交叉操作是在区间[0,1]内随机生成若干均匀分布的Rand,随机数个数等于目标个体ti中的变量个数,且各随机数Rand与变量一一对应。则可采用二项交叉操作生成测试个体vi: (13) 式中:cr表示交叉概率;rnd为区间[1,d]内均匀分布的整数,以确保至少一维分量是从ti贡献给vi;否则,可能会出现vi与ti相同的情况,不利于新个体产生。 二项交叉操作过程,见图2。 图2 二项交叉操作过程Fig.2 Binomial crossover operation process DE算法采用的选择操作方式,仅当vi的适应度优于xi,才会被选入下一代。选择操作方式如下: (14) 这使得更多优秀个体进入下一代种群中,通过这种逐代提高种群多样性的方法达到最优解或满意解。 为了简化穿越走廊网络优化设计过程,提高优化效率,并易于DE算法的编程实现, 本文选择最常用的DE/Rand/1/bin,其中bin表示二项交叉操作。 本文将差分进化(DE)算法与改进的极限学习机(MELM)有机结合,提出了一种基于DE-MELM的土质边坡稳定性预测方法,其具体步骤如下: (1) 数据预处理。考虑到土质边坡稳定性影响因素之间存在量纲差别,需要对数据进行标准化处理,将数据归入[-1,1]范围内。 (2) DE算法优化MELM。将土质边坡稳定性影响因素作为输入,土质边坡稳定性系数作为输出,在训练样本的基础上,对MELM算法的权值矩阵和阈值进行优化,获得最优解。 (3) 利用最优参数训练MELM。基于训练样本,利用DE算法获取的最优参数,训练土质边坡稳定性MELM预测模型。 (4) 土质边坡稳定性预测。将测试样本对应的影响因素数据输入训练好的土质边坡稳定性MELM预测模型进行预测,分别计算绝对误差和相对误差,并根据预测结果对本文方法的性能进行评价。 基于DE-MELM的土质边坡稳定性预测流程,见图3。 图3 基于DE-MELM的土质边坡稳定性预测流程Fig.3 Prediction process of soil slope stability based on DE-MELM 本次试验的研究对象为胀缩性裂隙土质边坡失稳问题。胀缩性裂隙土质边坡失稳的危害大,轻则影响工程质量和施工进度,重则造成大量人员和财产损失。研究表明:影响此类土质边坡失稳的因素很多,诸如降雨的强度与持时,裂隙的位置、深度与间距等。这些因素在不同阶段,对土质边坡稳定性造成的影响迥然不同,作用机理也非常复杂,使土质边坡失稳问题呈现出很大的随机性、模糊性和信息不完整性,这无疑增加了此类土质边坡稳定性预测的难度。 通过文献查阅,结合胀缩性裂隙土质边坡的统计规律,并广泛征求专家建议和意见,通过问卷调查和数理分析,得到了影响此类土质边坡稳定性的主要因素为:降雨强度(A)、土体重度(B)、土体黏聚力(C)、土体内摩擦角(D)、土体饱和渗透系数(E)、土体饱和含水量(F)、裂隙深度(G)、坡高(H)、坡比(I)。试验中采用的数据样本来源于文献[15],这些数据均基于以上9个主要因素的正交试验而获得,相对于考虑所有相关因素的试验,采用正交试验产生样本数据的优点是在不损失试验信息、不影响可信度的前提下,能够有效降低试验的次数。正交试验共获得40组样本数据,选取其中32组数据作为训练样本,余下的8组数据作为测试样本,见表1。其中,将影响此类土质边坡失稳的9个因素作为输入,土体边坡稳定性系数作为输出,通过优化参数,构建DE-MELM模型,对土质边坡稳定性进行预测。 表1 土质边坡稳定性训练与测试样本Table 1 Training and test samples of soil slope stability 本次试验环境为:Intel(R)Core(TM)i7-7820X CPU@3.60GHz,4 GB DDR内存,80GB+720转硬盘;Windows 10操作系统。算法验证通过MATLAB编程实现。选取均方根误差(RMSE)作为网络输出性能的评价指标。 与ELM一样,MELM的输入权值和隐含层偏差也是随机给定的,导致土质边坡稳定性的预测精度还存在上升空间,为了充分利用更多的隐含层节点,本文采用DE算法对MELM的隐含层输入权值和偏差进行搜索寻优,以提高网络效率。DE算法最大的迭代次数设置为200,不同预测方法(ELM、MELM和DE-MELM方法)分别用于土质边坡稳定性预测的均方根误差即标准误差(RMSE)随隐含层节点数的变化曲线,见图4。 图4 不同预测方法的标准误差(RMSE)随隐含层节点 数的变化曲线Fig.4 Variation curves of standard errors of different prediction methods with the nodes number of the hidden layer 由图4可见,随着隐含层节点数的增加,不同预测方法的RMSE下降趋势越明显;在相同隐含层节点数范围内,DE-MELM方法的RMSE更小,并且当达到一定隐含层节点数,DE-MELM方法的RMSE较MELM方法并没有显著下降,这就表明DE-MELM方法大大提高了隐含层节点的使用效率,即通过使用更少的隐含层节点取得了更高的土质边坡稳定性预测精度。 为了验证DE-MELM方法用于土质边坡稳定性预测的效果,采用ELM、MELM和DE-MELM方法对同样训练集和测试集分别进行学习和预测,并比较各方法的性能,见图5。 图5 不同预测方法的收敛速度及精度对比Fig.5 Comparison of convergence speed and accuracy of different prediction methods 由图5可见,在土质边坡稳定性预测过程中,DE-MELM方法的收敛速度及精度明显优于ELM和MELM方法,在15次迭代后收敛精度就已较高了,而ELM和MELM方法的初始收敛速度较快但收敛速度及精度明显不如DE-MELM方法。 表2给出隐含层节点数为20时不同预测方法土质边坡稳定性预测结果的对比,图6为不同预测方法土质边坡稳定性预测曲线的对比。 表2 不同预测方法土质边坡稳定性预测结果的对比Table 2 Comparison of prediction results of different methods for soil slope stability 图6 不同预测方法土质边坡稳定性预测曲线的对比Fig.6 Comparison of prediction curves of different methods for soil slope stability 由于ELM的输出权重直接由最小二乘估计方法得出,如果训练数据存在差干扰,则会使输出层权值的最小二乘估计结果受到影响,从而导致预测结果失真。为此,采用本文提出的基于MELM的土质边坡稳定性预测方法,以减少监测数据中粗差对预测结果的干扰。 为了验证MELM对粗差的抵御性,在表1中的32个训练样本中,将样本序号5、16和27的稳定性系数值中分别加入0.4的粗差,并利用加入粗差后的样本数据分别进行ELM、MELM和DE-MELM方法预测。其网络拓扑结构均为:输入节点为9,隐含层节点数为20,输出节点为1,激励函数为Sigmoid函数,迭代权函数为一次范数法,以最大迭代次数100次作为收敛条件。加入粗差后不同预测方法土质边坡稳定性预测结果的对比见表3,训练样本和测试样本加入粗差前后不同预测方法土质边坡稳定性预测误差的对比,见图7和图8。 表3 加入粗差后不同方法土质边坡稳定性预测结果的对比Table 3 Comparison of prediction results of different methods for soil slope stability with gross error 图7 未加粗差不同预测方法土质边坡稳定性预测误差的对比Fig.7 Comparison of prediction errors of different methods without gross error 图8 加入粗差后不同预测方法土质边坡稳定性预测误差的对比Fig.8 Comparison of prediction errors of different methods with gross error 由图7和图8可见,当训练样本数据中含粗差时,利用ELM方法进行预测时,所得的预测值与真实值存在很大的偏差,且与不含粗差的预测误差相比,整体偏大;而利用MELM方法和DE- MELM方法经100余次迭代计算后,所得的预测值与真实值较为逼近,且与不含粗差的预测误差相比,两者较为接近,说明MELM和DE-MELM方法都具有抵抗粗差的性质,而DE-MELM方法因参数优化则预测精度更高。 总之,采用DE-MELM方法对土质边坡稳定性进行预测,不需要了解土质边坡变形和失稳的力学机理,也不需要了解网络内部复杂的映射关系,仅需在已有经验的情况下,通过网络自身的不断训练、学习和测试,建立起土质边坡稳定性与各影响因素之间复杂的非线性关系,并通过训练好的网络进行预测即可。通过对比不同预测方法的预测结果可以看出,DE-MELM方法对土质边坡的稳定性能做出较为准确、客观的预测,且能准确地刻画土质边坡稳定性与各影响因素之间的非线性关系,同时也能较好地适应自身不确定性的特点,进而证实了该方法是可行的。 针对土质边坡稳定性监测数据存在粗差,以及ELM参数随机确定的弊端,本文提出了一种基于DE算法优化参数的抗差ELM土质边坡稳定性预测方法,并得出如下主要结论: (1) DE-MELM方法不仅继承了ELM收敛快的特点,且对数据集中粗差具有较好的抗干扰能力,说明基于M估计的ELM方法能够减少粗差对预测结果的影响。 (2) DE-MELM方法采用DE算法优化MELM的隐含层输入权值和偏差,能够有效提高MELM的预测性能,且预测精度较高。 (3) 相对于ELM和基于M估计的ELM方法,DE-MELM方法的收敛速度更快、预测精度更高,且对粗差的抵御性更强。 (4) 仿真验证中本文仅使用了正交试验获得的样本数据,验证了DE-MELM方法的可行性,若能在收集真实数据的基础上对土质边坡稳定性进行预测,其预测结果会更准确,也更具有说服性。此外,本研究中仅利用了影响土质边坡稳定性的9个主要因素,要想提高预测精度,还需要视实际情况加入其他影响因素,如地下水条件、荷载等,这将是今后的研究方向。2.1 变异操作

2.2 交叉操作

2.3 选择操作
3 基于DE-MELM的土质边坡稳定性预测方法
4 实例验证
4.1 样本构建
4.2 参数分析
4.3 抗粗差性验证


5 结论与建议

