寿命服从Weibull分布时高价值弹药导弹抽样方法
牛跃听, 赵晖, 李妍, 穆希辉, 张国志
(1.沈阳理工大学 装备技术研究院, 辽宁 沈阳 110159; 2.32181部队, 河北 石家庄 050000; 3.哈尔滨理工大学 数学系, 黑龙江 哈尔滨 150080)
0 引言
近期局部战争表明,高价值弹药导弹已成为现代战争依赖的主要弹种。世界各国争相研制、装备大量的高价值简易制导弹药、导弹。研制生产单位通常会给出高价值弹药导弹一个大概的质保期,如10 a、5 a. 但是,由于高价值弹药结构的复杂性、构成材料的多样性,以及其承受不同环境载荷的差异性[1],导致这个给定的质保期往往和其实际寿命有很大差异,一般给出的质保期都较为保守。
针对临近质保期的高价值弹药导弹,世界各国通常的作法是:选取一定数量的高价值弹药导弹开展寿命试验[2-4],同时结合自然贮存历程中的环境载荷,分析光学、机械、电子、化学等部组件失效模式、失效机理[5],分析各部组件寿命匹配的差异性,扬长补短进行延寿修复[6-10],此举可节约大笔军费,经济效益显著。表1为美军和我军部分高价值弹药导弹延寿情况。
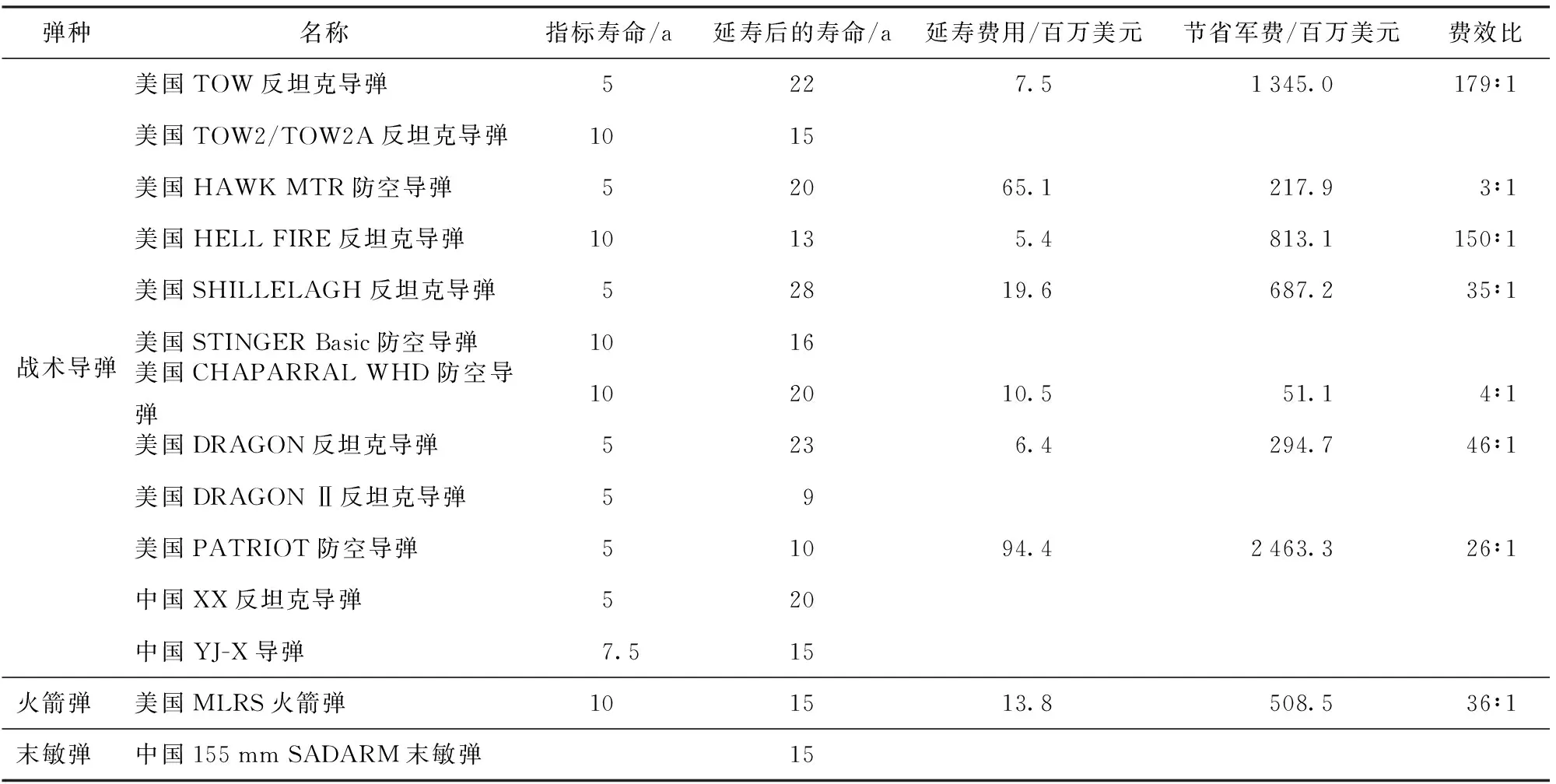
表1 部分战术导弹、火箭弹、末敏弹延寿情况
表1中的数据来源于美军导弹研究发展工程中心的导弹寿命周期系统工程面临的挑战[11]和我军有关研究成果。
在高价值弹药导弹贮存期间内的不同阶段,抽取一定数量的样本进行可靠性试验时,由于诸多方面的原因,不能像传统低价值弹药那样获取同年份批次、大样本来试验,通常希望通过最小数量的试验样本进行统计推断[12]。但是,样本容量少,推断的精度就要减小;另外,高价值弹药导弹贮存年限不一,如何对其抽样也对统计推断的精度产生影响。高价值弹药导弹样本数量的确定问题,至今领域内没有明确的科学依据,各单位只是根据工程实践经验,选取6~12个样本进行评估,缺乏必要的理论依据,有很大的主观随意性,对于“抽取多少枚样本进行寿命评估、抽取贮存了多长时间的样本、抽取的样本量和寿命评估精度之间的关系”这一现实问题,很难给出令人信服的答案。
1 考虑贮存时间因素的高价值弹药导弹抽样模型
在统计学中,从母体中抽取一个子样, 确定最少样本个数,也就相当于确定最小子样容量。文献[13]研究了机械行业产品在疲劳寿命试验过程中最少样本容量的确定方法。高价值弹药导弹样本抽样有其自身特点:可供研究的样本数量少、样本的贮存限对寿命评估有一定的影响[14]、贮存期内有大量的质量监测数据。统计分析这些检测数据,假设其服从正态分布、指数分布、极值分布、Weibull分布等,运用统计学方法可以得到其最为合适的自然贮存寿命分布函数[15-16]。
贮存的高价值弹药导弹定期进行质量状态检测,抽样模型符合定时截尾特征。高价值弹药导弹抽样时间示意图如图1所示。图1中,X′为贮存期内高价值弹药导弹寿命变量,X为贮存t1时间后的高价值弹药导弹寿命变量,Xt2为贮存t2时间后的高价值弹药导弹寿命变量。
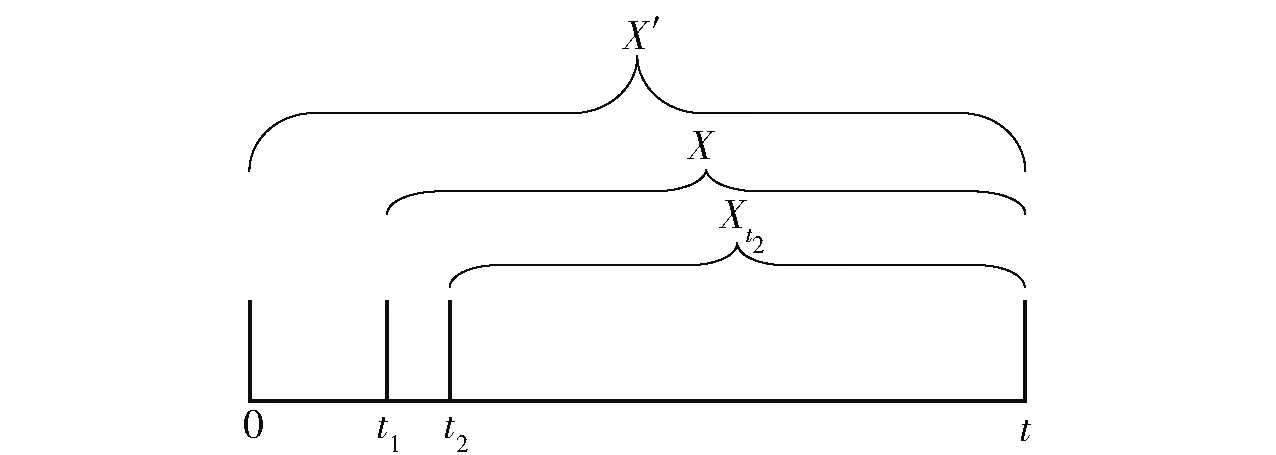
图1 高价值弹药导弹抽样时间图示Fig.1 Sample time for high-value ammunitions
取分别来自总体Xt1(贮存t1时间后)及Xt2(贮存t2时间后)的两组样本,采用定时截尾样本:
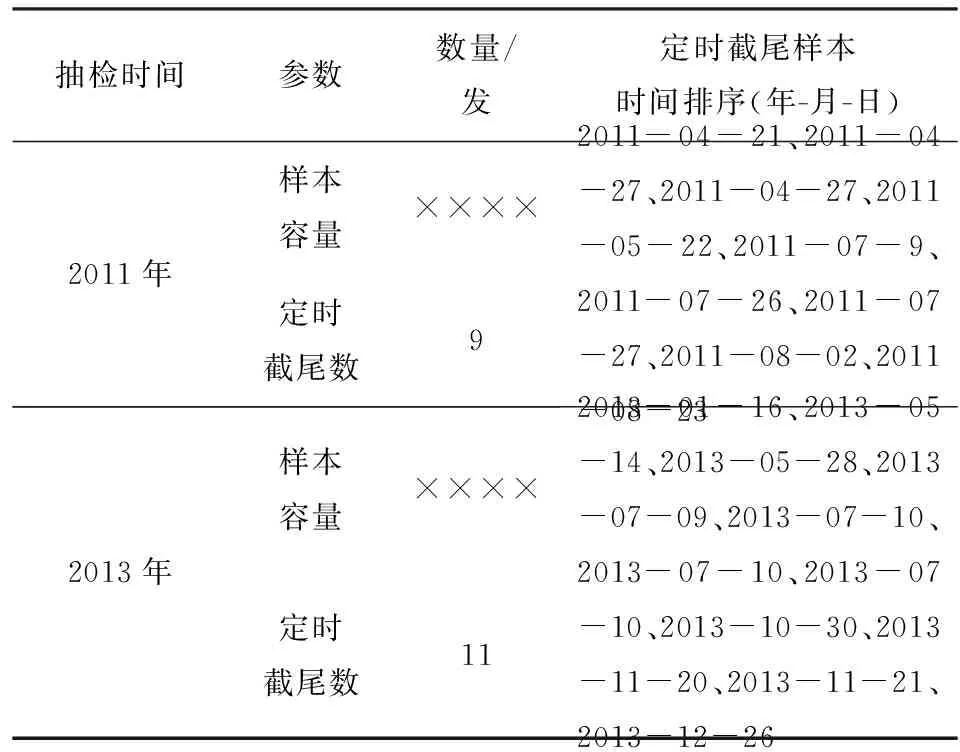
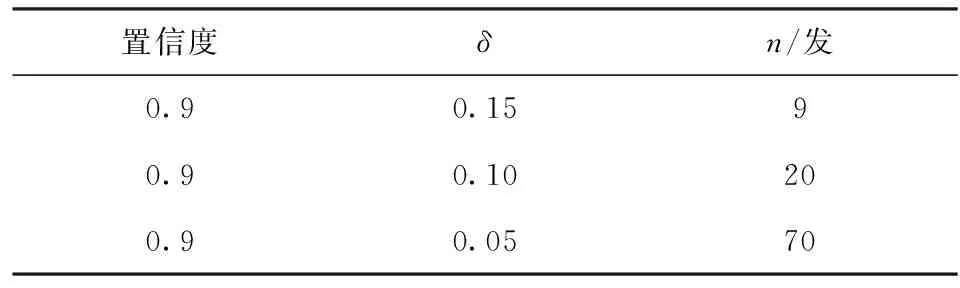
1) 设a1 2) 设q1 统计分析我国某型高价值弹药导弹长期检测数据,抽测数量为××××枚,通过寿命分布函数拟合,得出:其自然贮存寿命服从Weibull分布,且形状参数m=2.3. (1) 变换形式后,得 (2) (3) (4) (5) 由(5)式可得 (6) 数理统计学中有重期望公式: E(Z)=EE(Z|K). (7) 因此,在给定ht0条件下,(4)式可变换为 (8) 在高价值弹药导弹可靠性评估中,由于Xt0服从Weibull分布,所以高价值弹药导弹样本寿命的数学期望为 (9) 将μ置信度为1-α的置信下限估计记为L,可得 (10) 高价值弹药导弹可靠性评估采用如(11)式精度度量方式: (11) 式中:n为高价值弹药导弹样本的容量。 联立(8)式、(9)式、(10)式、(11)式,可得 (12) r2即为满足一定评估精度要求条件下,所需要的最小失效样本数量。由于高价值弹药导弹可供研究的样本数量少,因此在工程实践中为了使其样本量达到最小(满足一定评估精度前提下),可取最小样本容量与r2相等,即:通过寿命试验,使得选取最小样本容量的高价值弹药导弹全部失效,进而通过统计分析的方法评估其寿命。 设定某个精度δ>0,精度要求满足δn≤δ条件的最小样本容量n可由(13)式求出: (13) 运用(13)式可以计算得出满足一定可靠性评估精度要求下,不同贮存时间高价值弹药导弹的最小样本容量。 由数理统计学F分布函数的定义可知: (14) (15) 那么,由数理统计学可知: ht0置信度为1-α的置信区间为 (16) 若ht0服从均匀分布,即ht0~U(a,b),0 (17) (18) 抽测了某型高价值弹药导弹长期检测数据,抽测数量范围××××枚,通过寿命分布函数拟合,获得某型高价值弹药导弹寿命符合Weibull分布,且形状参数m=2.3. 其中分别在2011年和2013年抽测的2005年生产某型高价值弹药导弹统计失效情况如见表2所示,并对数据进行了分析(见表3和表4)。 表2 2005年生产的某型高价值弹药检测情况 表3 2011年检测数据分析 表4 2013年检测数据分析 取置信度1-α=0.9,查表得: 由(16)式可得ht0(0 表5 最小样本容量与可靠性评估精度计算结果 由表5分析可知: 1) 针对2005年生产的某型高价值弹药导弹,在2013年抽样并进行可靠性试验时,在置信度0.9、可靠性评估精度指标0.15条件下,最小样本容量取9. 2) 在同一置信度下,可靠性评估精度指标要求越高(δ数值越小),需要的某型高价值弹药导弹最小样本数量越多。 1) 高价值弹药导弹寿命评估中,可供试验研究的样本少,对评估精度影响较大,需要利用统计推断的理论方法,合理地确定最小样本容量,为科学评估其贮存寿命提供理论支撑。 2) 高价值弹药寿命服从Weibull分布时,本文定义了其精度度量方式,研究了样本容量、贮存时间、可靠性评估精度之间的内在关系,给出了揭示三者关系的数学公式,解决了单发价值高、可供试验研究的样本少、贮存年限不一的高价值弹药导弹可靠性试验最小样本容量问题。 3) 任何理论都有使用范围,本研究中的模型要求p0(p0是[0,t0]区间高价值弹药导弹的失效率)比较小。工程实际中,贮存10 a的某型高价值弹药导弹失效率低于5‰,符合这一要求。如果p0大了,模型的误差就会变大,本文中结论就不再成立。

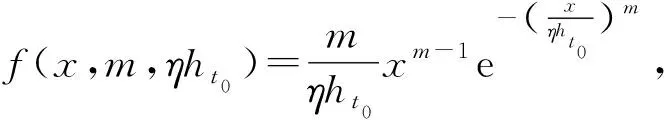
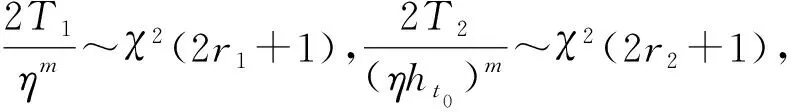
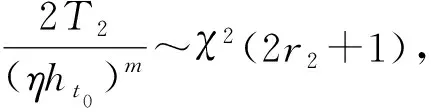
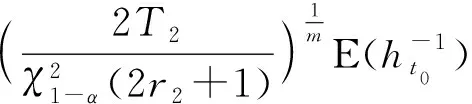
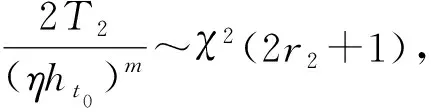
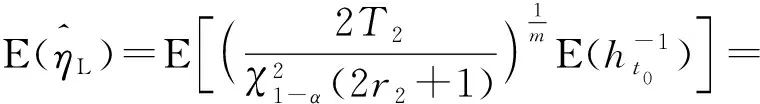
2 ht0的估计
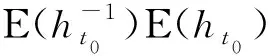

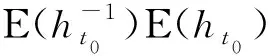
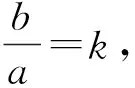
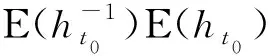
4 算例







5 结论

