基于薄层单元法的弹体与引信系统螺纹连接模拟参数识别

鄢阿敏， 王晓锋， 王健， 皮爱国， 黄风雷

(1.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081； 2.北京系统工程研究所， 北京 100034)

0 引言

螺纹连接具有强度高、连接可靠、拆卸方便等优点，是组合结构里面一种广泛应用的连接形式，侵彻弹体与引信的连接形式一般为螺纹连接。由于螺纹接触含有许多不确定因素，导致了引信体振动响应无法准确预测。众所周知，螺纹连接不确定性因素的主要来源是接触刚度与摩擦阻尼两方面的非线性因素[1]。由于常用模态分析软件无法定义非线性因素，通常在数值分析时将螺纹连接简化为固连状态或定义为简单的实体螺纹接触，这种处理方式虽然极大地提高了计算效率，但是造成计算结果比实际值偏大。在高速侵彻多层硬目标信号识别领域，准确评估弹体与引信系统振动响应特性尤为重要。为提高仿真模型的计算精度，需要在仿真模型中对螺纹连接的接触刚度与阻尼进行准确的模拟。因此探索出一种针对螺纹接触准确的建模方式对研究弹体与引信系统振动响应具有十分重要的意义。

针对螺纹连接仿真建模，许多学者开展了工作。Mackerle[2]对1990年～2002年12年间出版的各种连接类型在不同加载状态下有限元建模方式进行归纳与总结，其中大量工作是关于螺纹连接建模分析的。也有一些学者开展了关于螺纹连接静态行为的研究工作[3-4]，还有一部分工作是针对螺纹动态特性进行开展的。例如：Zhang等[5]通过建立实体螺纹的方式对螺纹碰撞过程进行研究,得出了螺纹连接的碰撞频率；Brutti 等[6]采用有限元模型对管螺纹的动态性能进行了研究，表明螺纹管构件的动态特性对结构的强度影响至关重要。

在组合结构动态响应仿真建模这一领域，许多学者就如何对连接界面准确表征这一问题进行了大量的探索，尤其集中在以薄层单元表征接触界面的研究内容上。这其中代表性的工作陈述如下：Desai[7]1984年首次提出薄层单元建模概念，通过赋予薄层单元法向接触刚度与剪切刚度来表征岩石、土壤接触界面；Bograd等[8]对接触界面模拟方式进行分析比较，阐述了薄层单元建模方式的优势；Iranzad等[9]为表征局部非线性刚度与阻尼对螺栓搭接组合结构响应的重要影响，采用薄层虚拟弹塑性材料对接触界面进行建模；姜东等[10]针对螺栓连接建模与参数识别问题开展研究，提出了螺栓连接结构接触面力学性能识别方法；Zhao等[11]采用薄层单元模拟螺栓连接接触刚度，得出螺栓预紧力对螺栓界面接触刚度影响的一般规律；Adel等[12]采用一个双连接薄层单元模型模拟混合结构中螺栓连接界面，基于该模型计算了混合螺栓连接结构的模态频率，该模型可用于复杂结构和大型结构的混合节点界面的模态分析中；Lothar等[13]将薄层单元应用于发电机双盘转子收缩接头有限元模型中，并将试验获取的连接阻尼与刚度参数耦合到层单元模型中，该模型可以作为预测发电机响应特性的工具；Alamdari等[14]将薄层单元引入螺母接口相互连接螺纹管有限元分析中，薄层单元采用非线性本构模型表征非线性状态下节点的能量耗散和软化现象。综上所述，对于螺纹连接仿真分析，若是分析静态与动态加载下力学行为，主要通过接触的设置来表征非线性因素。如果对模态分析与频率响应分析等动力学响应问题的研究，通过在接触界面引入薄层单元表征非线性因素，这种方式目前主要应用于模拟螺栓连接接触界面，并取得了比较好的效果。所以本文提出将薄层单元建模的方式应用于螺纹连接结构中，来解决螺纹动力学分析过程非线性因素无法识别的问题。

本文将薄层单元引入仿真建模中，来合理有效地模拟螺纹连接接触刚度与摩擦阻尼等非线性因素的影响，仿真计算精度得到显著改善。首先采用试验方法研究松、紧不同连接状态对模态频率与频率响应曲线的影响；其次利用多点约束(MPC)技术建立了螺纹连接的薄层单元模型，采用Nastran设计灵敏度分析模块，对薄层单元的材料参数进行识别，基于试验获得的模态频率与频率响应曲线对识别后的薄层单元材料参数进行验证；最后将薄层单元建模方式推广应用于弹体与引信螺纹连接结构中。

1 薄层单元基本理论

采用薄层单元模拟螺纹连接接触面，薄层单元尺寸l×s×t,其中l为薄层单元的长度，s为薄层单元圆周长度，t为薄层单元的厚度。根据虚位移原理，得虚功方程为

(1)

式中：V1为薄层单元在局部坐标系下的体积；σ为单元的应力；ε为单元的应变；{u}n为节点位移；K为薄层单元刚度矩阵，可通过等参变换计算：

(2)

B为变换矩阵，D为本构矩阵，ξ、η、ζ为自然坐标符号，J为雅克比矩阵，表征局部坐标与自然坐标的偏微分关系。在自然坐标系下，数值积分形式更简便，可以将雅克比矩阵J进一步简化为

(3)

(3)式代入(2)式中，可得到薄层单元刚度矩阵K的数值计算表达式为

det([J(ξi,ηj,ζk)])wζ,iwη,jwξ,k，

(4)

式中：wζ,i、wη,j、wξ,k为高斯积分权函数。

对于薄层单元，薄层单元的厚度t远远小于另两个方向的特征尺寸l和s，根据Desai[7]的描述，采用泊松比为0的材料本构关系时，薄层单元法向刚度与切向刚度将会解耦，单元的面内应变分量(εx,εy,γxy)和应力分量(σx,σy,τxy)将被忽略。若接触的法向{e}n和两个切向{e}tx与{e}ty分别定义为薄层单元局部坐标系的z轴、x轴、y轴方向，根据以上分析，设连接界面法向与切向接触性能相互独立，两个切向的接触性能具有一致性，表征界面接触性能的薄层单元本构方程为

(5)

式中：Esn、Gst分别是薄层单元的法向弹性模量和切向剪切模量。

在有限元计算中，若采用各向同性材料模拟薄层单元，其本构方程为

(6)

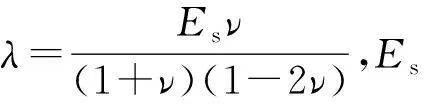
根据薄层单元的基本理论，εx=εy=εxy≈0，材料的本构方程将退化为

(7)

各向同性材料仅含两个材料参数：弹性模量Es和剪切模量Gs. 在动力学仿真分析过程中，弹性模量与剪切模量影响模型的模态刚度，密度影响模型的模态质量，所以采用各向同性材料进行表征薄层单元模型，只需要确定薄层单元密度与弹性模量(或剪切模量)两个参数。后面将基于模态试验结果，将薄层单元的密度与弹性模量设置为设计优化变量，采用Nastran设计优化模块对薄层单元的材料参数进行识别。

2 螺纹试件与无螺纹试件模态试验研究

2.1 试验装置

为了给薄层单元建模参数的确定提供试验数据支撑，开展螺纹连接组合结构的模态试验。试验试件由两段空心圆柱管通过螺纹连接组成，如图1所示。螺纹规格M36×2-6H/6g-40，内、外螺纹之间为间隙配合，6级加工精度，螺距为2 mm，旋合长度为40 mm. 为了验证仿真计算螺纹的材料参数，设计同尺寸无螺纹试件同组进行试验。

图1 螺纹连接Fig.1 Thread connection

田晶等[15]采用多种悬挂方式与弹性支撑方式进行自由模态试验，表明采用弹性绳悬挂的方式最接近自由边界状态，参考该方法，本文采用弹性绳对试件进行悬挂来模拟自由边界条件。利用电磁激振器对螺纹试件进行激励，如图2激振器与传感器分布示意图所示，激励点选择在Z1位置处。两个三向加速度传感器粘贴在试件的A1与A2位置。利用比利时LMS公司模态分析软件进行辅助测量与分析，选择正弦扫频信号作为激励信号；采用1个16通道的模态分析仪接收和处理信号。模态分析仪产生的正弦扫频信号经过运算放大后输入电磁激振器，激振器接收信号产生激振力，激振器连接杆端部安装有力传感器，采集激振力传入模态分析仪中，这样就形成对激振力的反馈回路控制。

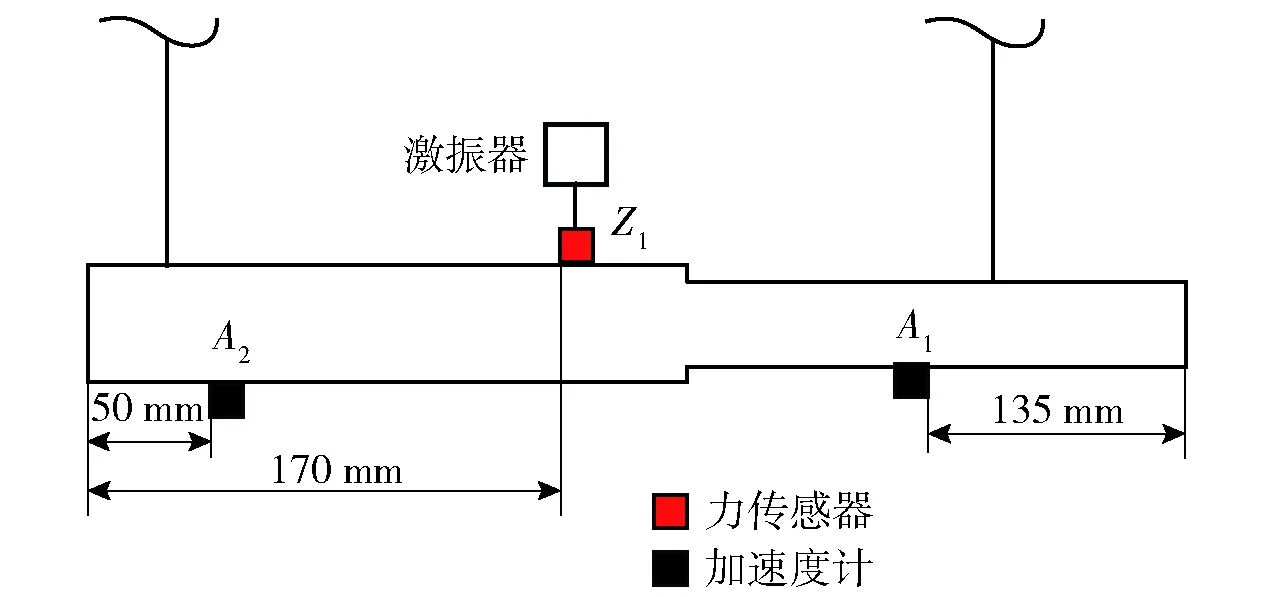
图2 激振器与传感器分布示意图Fig.2 Schematic diagram of exciter and sensor layout

2.2 试验过程与结果分析

2.2.1 无螺纹试件的模态试验

无螺纹试件不含非线性因素。试验中选择正弦扫频信号为激励信号，该类扫频信号可以保证测试的重复性，能够很方便地测出模态频率与频率响应曲线[16]。扫频范围为100～5 000 Hz，保证了扫频范围能够覆盖结构前3阶模态频率，扫频速度为10 Hz/s，激励力的幅值为0.1 N. 端部A2处测量得到的前3阶频率响应曲线如图3所示，前3阶模态频率分别为938.3 Hz、2 669.8 Hz、4 582.5 Hz. 试验结果表明，频率响应曲线存在明显的尖峰，且曲线关于共振峰是严格对称的，说明各阶模态阻尼较小，频率响应曲线具有明显的线性特征。

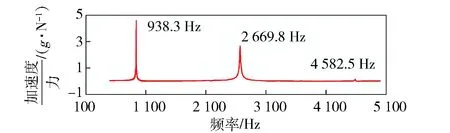
图3 无螺纹试件前3阶频率响应曲线Fig.3 Frequency response curve of threadless specimen

2.2.2 螺纹连接试件的模态试验

由于螺纹连接中存在非线性因素的影响，导致模态频率出现下降。当激励力较小时，螺纹接触表现出黏滞特征，随着激励力的逐渐增加，螺纹连接非线性因素的影响会逐渐增大，由黏滞特征向微滑移甚至宏滑移过渡。影响螺纹连接接触特性的因素有很多，例如粗糙度、润滑情况、预紧力等，为了突出研究主体与核心变量，选择螺纹预紧状态作为研究的变量，分别研究螺纹紧连接与松连接两种连接状态。因螺纹松、紧连接状态无法准确量化，为了便于分析，采取了在紧连接螺纹基础上将螺纹回旋1圈的方式来表征螺纹松连接状态。采用0.8 N、0.1 N两种激励力幅值进行激励；为了提高测量的精度，对各阶频率进行分段扫频激励，激励频率分别为100～1 500 Hz、2 000～3 500 Hz、3 500～5 000 Hz，扫频速度为10 Hz/s. 试验结果如表1所示。

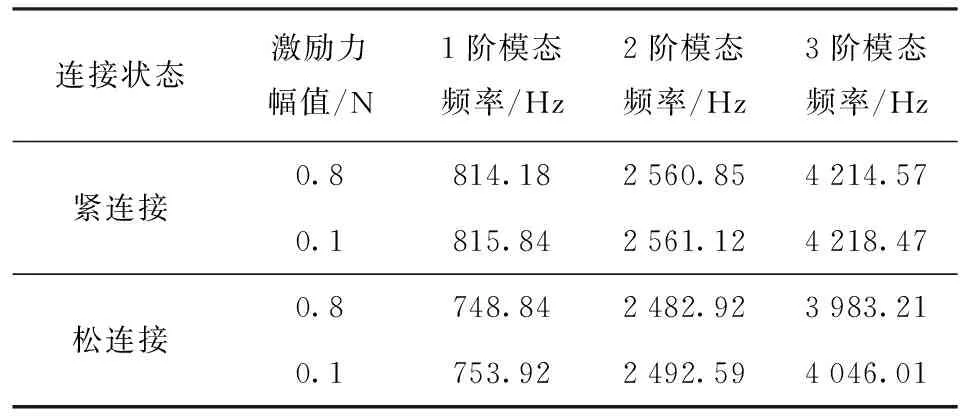
表1 4种工况下试验获得的前3阶模态频率

通过表1中的数据对比分析发现，各阶模态频率与无螺纹试件相比出现不同程度的下降，松连接状态下模态频率下降的幅度更大，且随着激励力幅值从0.1 N增加到0.8 N，紧连接螺纹模态频率基本上未发生变化，松连接螺纹模态频率变化较大，表明激励力的变化未改变紧螺纹的接触状态，而使松螺纹的接触状态出现了变化。

图4为试验与数值仿真获得的1阶频率响应曲线对比图。比较无螺纹试件的频率响应曲线可知，数值仿真获得的无螺纹试件1阶频率响应曲线与试验频率响应曲线形态一致，峰值频率为948.5 Hz，与试验值比较误差为1.09%. 对比无螺纹试件与螺纹试件的频率响应曲线发现，1阶模态频率从938 Hz分别下降到815 Hz和753 Hz左右，且松连接螺纹模态频率下降更明显，表明松连接状态相比较紧连接状态受非线性因素的影响更加明显。最后比较松连接螺纹与紧连接螺纹的频率响应曲线可得，激励力的变化会影响螺纹的接触状态。随着激励力增加,松连接螺纹模态频率从753.92 Hz下降到748.84 Hz，频率响应曲线幅值从1.32下降到1.18，分析原因为随着激励力的增加，螺纹接触面状态已从黏滞状态转变为微滑移状态，摩擦阻尼增大，造成幅值与模态频率的同时下降；而对于螺纹连接紧密的情况下，随着激励力变化，1阶模态频率从815.84 Hz变到814.18 Hz，频率响应曲线幅值从1.55增加到2.02，与松连接情况表现出完全不一样的形态，原因为紧连接状态下螺纹之间的接触为黏滞状态，当激励力幅值增大到0.8 N时也未改变螺纹实际接触形态。综上所述，为保证仿真模型与结果的精度，不宜将螺纹接触面的节点直接进行固连处理，需要根据螺纹接触的实际情况，准确地表征螺纹的接触状态，才能保证仿真模型的精度。

图4 螺纹结构与无螺纹结构1阶频率响应曲线Fig.4 The first-order frequency response curves of thread and threadless structures

3 螺纹连接薄层单元建模

Shokrollahi等[17]在研究中将组合结构接触表面分别由法向方向进行扩展定义为接触影响区域，参考其研究成果，本文根据实际螺纹齿高分别由法向延伸t/2作为螺纹接触影响区域，如图5所示，采用厚度为t的薄层单元来模拟螺纹影响区域，薄层单元的长度为内外螺纹结合面长度。根据螺纹的齿高选择薄层单元的厚度为2 mm，最终仿真模型由3个部分组成：内螺纹管、外螺纹管、薄层单元。薄层单元外径为38 mm，内径为34 mm，长度为40 mm. 有限元网格模型如图6所示。内、外螺纹管与薄层单元均采用8节点实体单元建模，网格单元总数为57 250个。

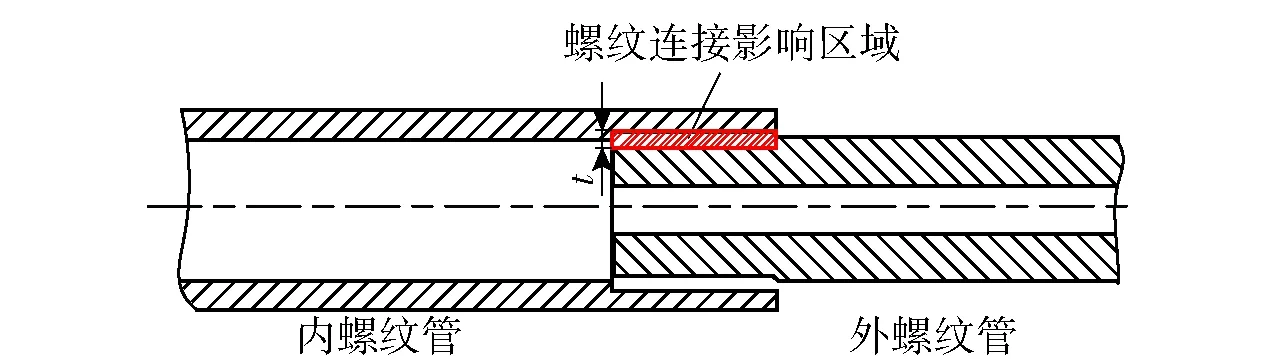
图5 螺纹连接影响区域示意图Fig.5 Schematic diagram of joint affected region

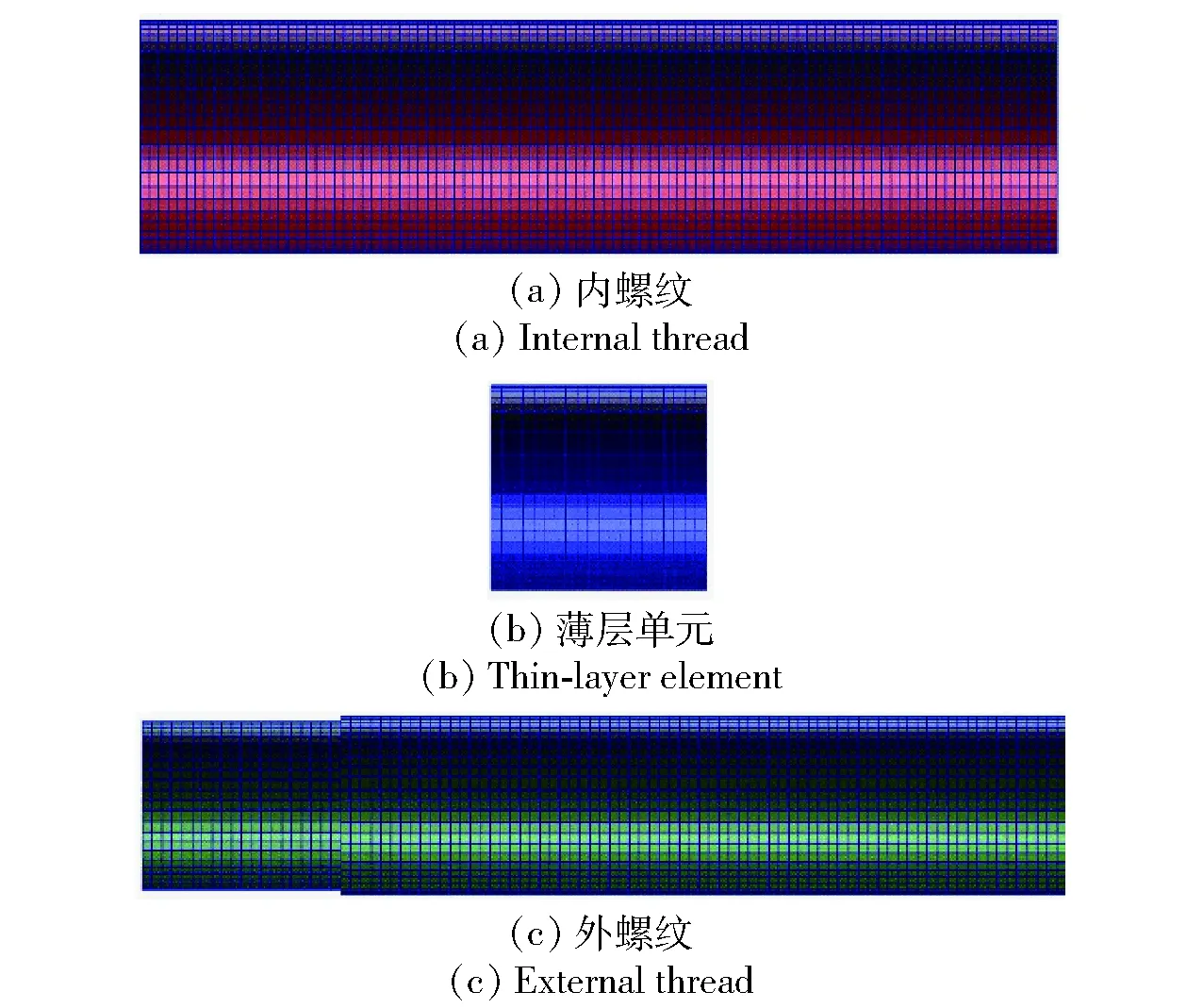
图6 内、外螺纹管与薄层单元有限元模型Fig.6 Finite element model of internal/external thread and thin-layer element

薄层单元与螺纹管的连接采用MPC技术，MPC连接允许在计算模型不同的自由度之间强加约束[18]，常用于对螺纹连接或螺栓连接等非线性问题的处理[19- 20]。如图7所示，将内螺纹与薄层单元外表面、外螺纹与薄层单元内表面建立MPC，并选择内、外螺纹处的节点设置为从节点；薄层单元对应处的节点设置为主节点，约束类型RBE2，如图8所示，共建立内、外两层连接，对应的节点处设置为1个MPC，约束总个数为2 100个。通过节点之间约束来进行力的传递。

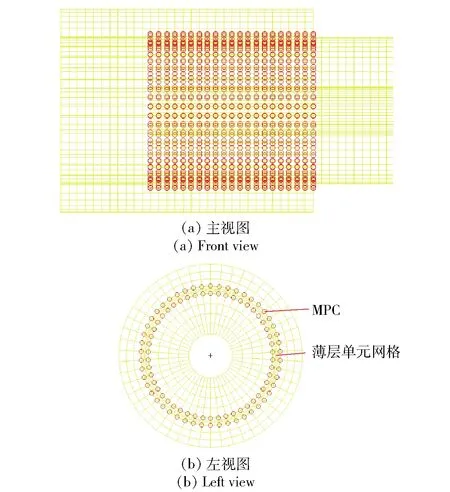
图7 薄层单元节点MPC约束示意图Fig.7 MPC constraint diagram of thin-layer element joint

在正式计算之前，需要对材料参数与模型进行验证，采用Nastran有限元软件对无螺纹试件进行仿真计算，螺纹管材料为45号钢，采用线弹性材料模型，材料参数[21]如表2所示。仿真结果如表3所示，仿真计算得出前3阶模态频率相比试验值偏差分别为1.09%、1.29%、0.21%，结果表明材料参数与材料模型是合理的。

图8 螺纹有限元模型Fig.8 Finite element model of thread connection

表2 材料参数[21]

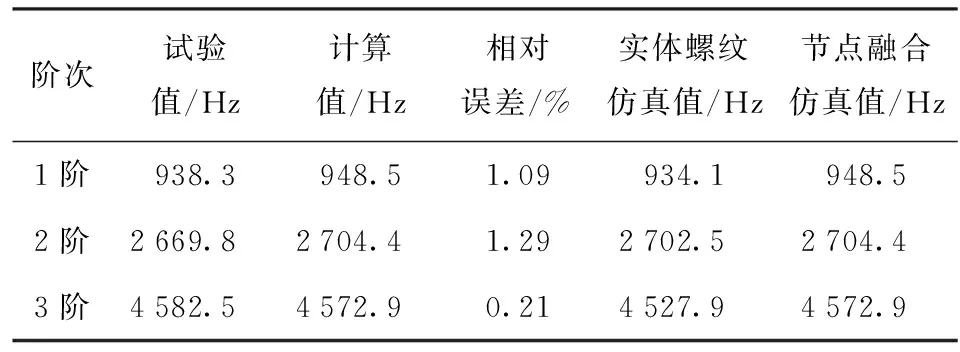
表3 模态频率仿真与试验结果

对于螺纹结构，为了简化分析，常用的方法将接触面处的节点直接融合，这样处理相当于将螺纹连接看成整体结构，忽略了螺纹结构，同时也忽略了螺纹连接之间的接触状态。为了进行分析对照，建立内、外螺纹管实体螺纹模型(见图8)，螺纹接触按照实际尺寸进行建模，为了提高计算效率，采用六面体单元进行网格划分，螺纹接触面上的节点进行绑定处理，然后进行模态分析，计算结果如表3所示。对比表3中节点融合与实体螺纹两种仿真处理方式可知，两种仿真方式的结果相差不大，说明动力学分析中，对计算结果起主要影响的是接触之间的非线性因素。

4 薄层单元参数识别

4.1 基于模态频率薄层单元参数识别

在动力学仿真计算过程中，由于常用的仿真软件不能识别螺纹的非线性因素，所以对接触刚度与阻尼等非线性因素不进行考虑，在仿真建模时直接将接触面的节点融合，这样与实际的螺纹连接情况相比，会使连接处的刚度增大、阻尼减小，最终导致仿真计算结果偏大。通过在螺纹连接处引入薄层单元来模拟螺纹连接处的接触刚度与摩擦阻尼，为了准确地表征接触刚度与摩擦阻尼，需要合理地选择薄层单元材料参数，采用的方法主要是通过调节薄层单元的材料参数使薄层单元仿真模型的预测值与实际观察值之间的差值最小，最终获得的薄层单元材料参数即为最合理的材料参数。采用Nastran设计灵敏度分析模块进行薄层单元参数识别，选择薄层单元弹性模量与密度作为设计优化变量，优化目标函数为

(8)

式中：Ci为各阶频率的权重因子；ωFEMi、ωti为模型预测与试验观测第i阶模态频率。

Nastran设计灵敏度程序由Muira在1988年提出，是一种迭代线性本征灵敏度方法，基本表达式为

(9)

式中：Δλn为特征值的变化；φn为变换矩阵；ΔK、ΔM分别为刚度与质量的变化。

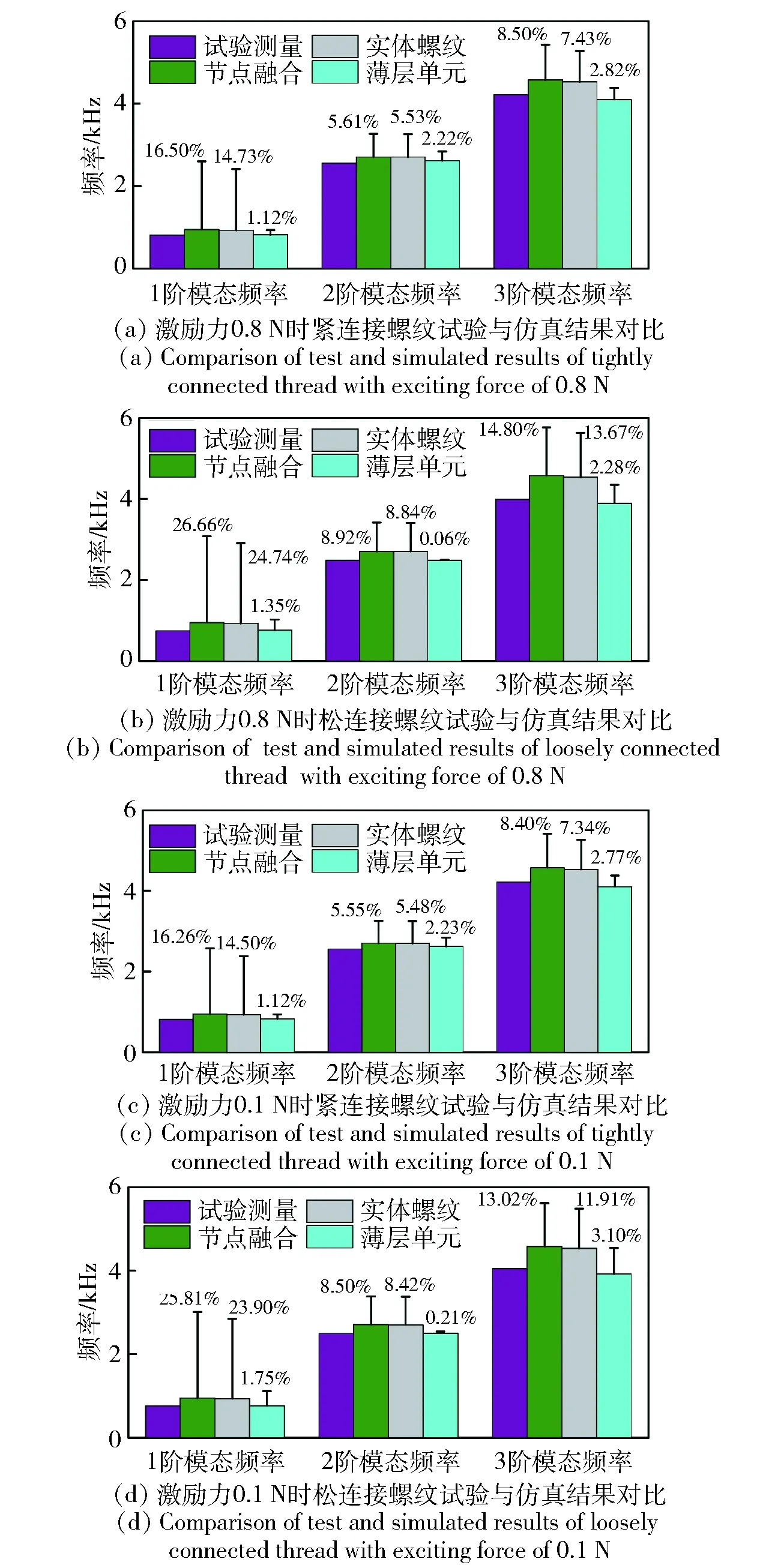
图9 试验测量与节点融合、实体螺纹、薄层单元模型3种仿真计算结果对比Fig.9 Comparison of test and simulated results of node merging, solid thread and thin-layer element model

薄层单元采用线弹性材料模型，初始材料参数与螺纹材料一致，弹性模量为211 GPa，密度为7 890 kg/m3. 各阶模态频率的权重因子为1，然后对薄层单元的材料参数进行识别，识别后的薄层单元模型计算结果如图9所示。对图9中数据对比发现，采用实体螺纹进行建模，考虑了螺纹的形态，计算误差相比节点融合误差要小，但是二者计算结果相差不大。由于这两种建模方式均未考虑接触之间的非线性因素，造成计算结果均偏大，都不能很好地对试验结果进行描述。柱状图中误差棒显示：在螺纹紧连接状态，1阶模态频率的仿真值相比较激励力0.8 N时测量值误差最大，为16.50%；在螺纹松连接状态下，1阶模态频率的仿真值相比较激励力为0.8 N时测量值误差最大，为26.66%. 采用薄层单元的仿真计算方式，紧连接状态下的最大误差从16.50%下降到1.12%；松连接状态下的最大误差从26.66%下降到1.35%. 说明采用薄层单元可以准确地模拟螺纹之间的接触状态，且无论螺纹是处在紧连接状态还是松连接状态，薄层单元仿真计算结果与试验结果较一致。

为了研究模态频率ω关于设计变量的灵敏度，对目标(8)式进行灵敏度分析计算。由于4组试验数据性质一致，选取激励力为0.8 N、紧连接螺纹的试验数据为分析对象，当设计变量仅为E或ρ，以及同时为E与ρ3种情况时，计算结果如表4所示。由表4可知，相比弹性模量，模态频率优化目标对密度变化更敏感，采用密度作为优化变量迭代4次后收敛，而仅采用弹性模量作为优化变量需要9次才能收敛。

表4 模态频率灵敏度分析结果

4.2 基于频率响应曲线薄层单元参数识别

螺纹接触之间存在接触刚度与摩擦阻尼，会使频率响应曲线尖峰频率出现偏移，尖峰处的幅值发生变化。如试验部分测得的频率响应曲线显示，由于接触刚度与摩擦阻尼的影响，不同连接状态、不同的激励力幅值，试验测得的频率响应曲线会表现出不一样的形态。在仿真分析的过程中，如果不对螺纹接触状态进行考虑，将会引起很大的误差。利用薄层单元来模拟接触刚度与摩擦阻尼，使模型频率响应曲线预测的结果与试验结果一致。为了准确地对接触状态进行模拟，需要对薄层单元的材料参数进行识别，采用的方法是通过调整薄层单元的材料参数使频率响应曲线各个频率点处幅值与试验观察获得的幅值一致，最后获得薄层单元的参数即为识别得到的参数。参数识别的目标函数为

(10)

式中：n为所取频率点数目；aFEM(ωi)为预测频率响应曲线频率点ωi处的幅值；at(ωi)为试验观察频率响应曲线频率点ωi处的幅值。

利用Nastran结构动力学优化模块来对薄层单元的参数进行识别，其优化过程在频率响应函数灵敏度分析的基础上进行，频率响应函数对变量x灵敏度分析表达式为

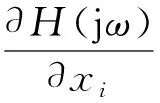
(11)

式中：m、c、k分别为广义质量矩阵、广义阻尼矩阵、广义刚度矩阵。

第3阶频率响应曲线的幅值与第1阶、第2阶相比可以忽略不计，所以只对第1阶与第2阶频率响应曲线进行考虑，将第1阶频率响应曲线作为目标函数(10)式中试验观察值，获取薄层单元参数，然后利用第2阶频率响应曲线对识别的材料参数进行验证。薄层单元初始材料参数与螺纹结构一致，激励方式、幅值、作用位置以及响应点位置与试验保持一致，选择薄层单元的密度与弹性模量为设计变量，1阶模态频率为约束变量，选择1阶模态频率附近一系列频率点组成目标函数。为提高计算效率，在构造目标函数的时候，在模态频率尖峰处间隔可以取得小一些，而在远离尖峰处频率间隔可以适当增大。

图10 试验与薄层单元模型的1阶频率响应曲线Fig.10 The first-order frequency response curves of experiment and thin-layer element model

紧连接螺纹的设计变量经过20次迭代后达到稳定，松连接螺纹的设计变量经过25次迭代后达到稳定。摩擦阻尼的控制主要通过调节模态阻尼参数，当设计变量逐渐收敛，达到稳定时，此时目标函数取得最小值，薄层单元参数识别结束。经过参数识别后，薄层单元模型计算得到1阶频率响应曲线与试验得出的频率响应曲线对比如图10所示。模型计算得到的频率响应曲线与试验频率响应曲线各频率点处吻合较好，整体上基本一致，表明参数识别后薄层单元可以准确地模拟螺纹接触面之间的接触刚度与摩擦阻尼，能够准确地描述试验现象。

利用2阶频率响应曲线对识别后的薄层单元材料参数进行验证。识别后的薄层单元参数计算出的2阶频率响应曲线与试验观测到的2阶频率响应曲线如图11所示，图中试验获得的2阶频率响应曲线左侧会出现突起，分析原因可能是由于外界干扰所导致。模型预测的2阶频率响应曲线与试验获得的2阶频率响应曲线尖峰处形态基本上一致，只是峰值频率有小幅度的偏移，螺纹松连接状态下，薄层单元模型计算2阶模态频率为2 502.12 Hz、2 507.93 Hz，相比试验结果误差分别为0.78%、0.64%. 螺纹紧连接状态下，模型预测得到的2阶模态频率分别为2 571.11 Hz、2 573.32 Hz. 相比试验值误差分别为0.43%、0.42%，由于2阶模态频率较大，频率响应曲线的偏移量相比真值可以忽略不计，表明经过识别后的材料参数是准确的，可以准确地表征螺纹连接接触状态。

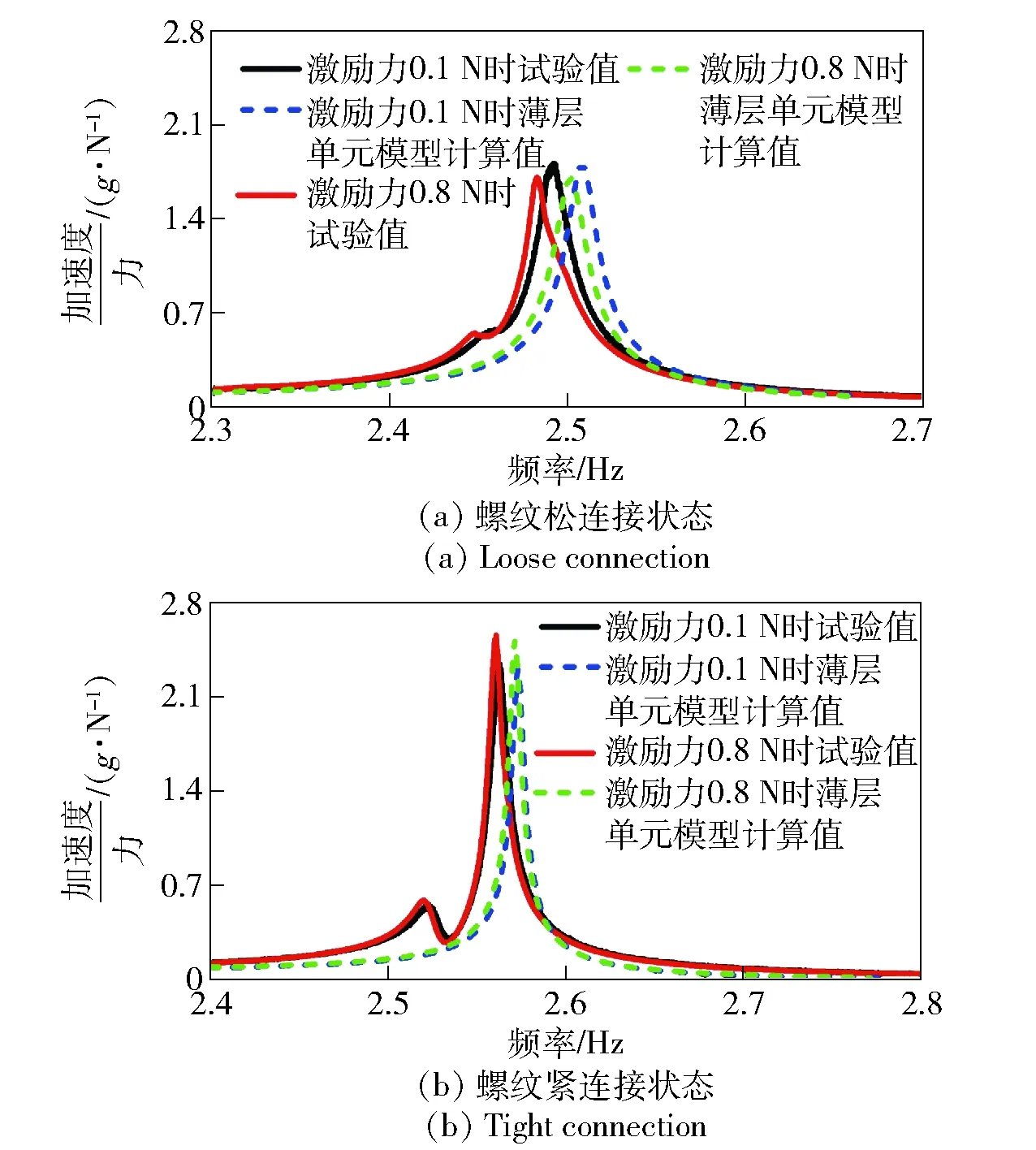
图11 试验与薄层单元模型2阶频率响应曲线Fig.11 The second-order frequency response curves of experiment and thin-layer element model

为研究频率响应曲线目标函数f关于设计变量的灵敏度，对目标(10)式进行灵敏度分析计算，同样选取激励力为0.8 N，紧连接螺纹的试验数据为分析对象，由于设计变量仅为E或ρ时，无法达到优化的目的，因此仅选择E与ρ同时作为设计变量的情况进行计算，结果见表5所示。可知，相比弹性模量，频率响应曲线优化目标对密度变化更敏感，可以将密度的变化作为粗调方式，而将弹性模量变化作为微调方式。

表5 频率响应曲线灵敏度分析结果

4.3 薄层单元厚度对识别精度的影响规律研究

当采用薄层单元模拟螺纹接触的刚度与摩擦阻尼时，薄层单元的厚度将影响参数的识别精度，下面将对这一问题进行研究。

图12为螺纹连接薄层单元示意图，F为螺纹连接所受的轴力，τ为薄层单元受轴力F后产生的剪切应力,剪切应力可以表示为

(12)

式中：Gs为剪切模量；γ为剪切角；A为接触面积；u为轴向位移。

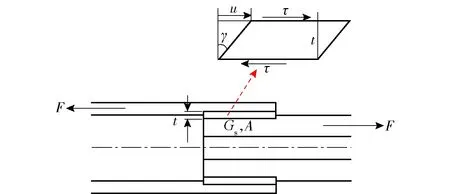
图12 螺纹连接薄层单元示意图Fig.12 Schematic diagram of thread-connected thin-layer element

对(12)式进行变换，可得

(13)

式中：K为螺纹连接的轴向刚度。

根据(13)式薄层单元的剪切模量Gs可以表示为

(14)

根据(14)式可知，薄层单元的厚度t与剪切模量Gs呈正比，说明薄层单元厚度的选择会对剪切模量的识别存在影响。定义薄层单元厚度的一半t/2与螺纹齿高H比值为薄层单元无量纲厚度，选取薄层单元无量纲厚度t/(2H)分别为0.46、0.92、1.39、1.85，然后分别对4种厚度的薄层单元进行材料参数的识别，并以(8)式、(10)式两个目标函数计算值作为评价标准。如果收敛后目标函数最小，说明参数的识别效果最好，采用松连接条件下，激励力0.1 N的试验数据作为目标表达式里面的观察数据，结果如图13所示。根据图13中的数据比较分析可得：薄层单元的厚度不同，模态频率目标函数相差不大，但频率响应曲线目标函数有较大的差别；当薄层单元无量纲厚度为0.92时，目标函数最小，采用此厚度的薄层单元计算结果准确度最高。综上所述，可以将两倍的齿高(2H)作为薄层单元建模的参考，但是为了建模的方便，一般在两倍的齿高周围取整数值作为建模的依据。

图13 不同薄层单元厚度目标函数值对比Fig.13 Comparison of objective function values of thin-layer elements with different thicknesses

5 弹体与引信螺纹连接薄层单元建模研究

侵彻弹体与引信体的连接形式为螺纹连接，如图14所示。螺纹型号为M42×2-6H/6g-33，螺距为2 mm，旋合长度为33 mm. 采用薄层单元模拟弹体与引信系统螺纹连接，有限元模型如图15所示，有限元模型由3部分组成：弹体、引信体、薄层单元。其中薄层单元厚度为2 mm，长度为33 mm，均采用六面体网格进行划分，且在螺纹连接处网格适当加密。薄层单元与弹体、引信体之间的节点连接采用MPC方式。弹体与引信材料均为高强钢30CrMnSiNi2A，材料参数如表6所示，薄层单元初始材料参数与弹体保持一致，采用线弹性材料模型进行表征。在薄层单元参数识别之前需要对弹体与引信系统进行模态试验，试验结果如表7中所示。根据模态试验的测量结果，利用目标表达式(8)式对薄层单元的参数进行识别，然后将识别后的材料参数传递入薄层单元模型中，最终计算结果如表7所示。

图14 弹体与引信螺纹连接Fig.14 Thread connection of projectile-fuze system

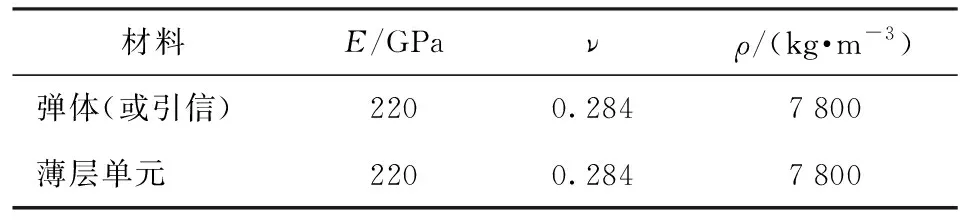
表6 材料参数

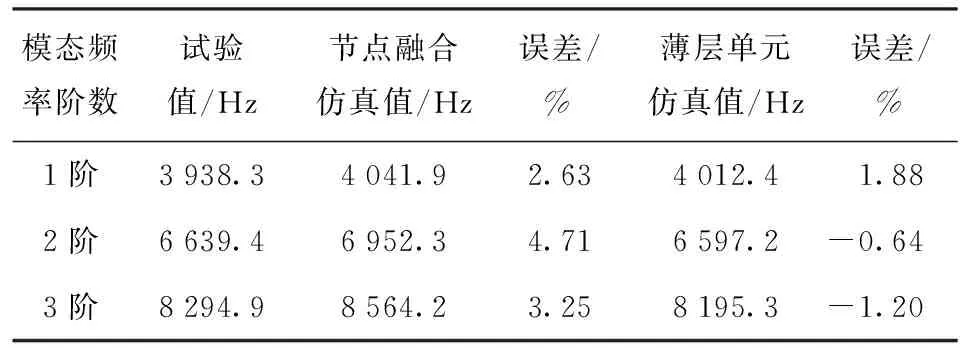
表7 弹体与引信系统试验与仿真结果对比

由表5中的数据对比发现，采用节点融合模型的计算结果与试验结果进行比较，误差分别为2.63%、4.71%、3.25%，采用薄层单元模型进行计算，误差下降到1.88%、-0.64%、-1.20%，表明在弹体与引信系统动力学分析过程中，采用薄层单元的建模方式可以有效地提高仿真模型的计算精度。

6 结论

螺纹连接接触刚度与摩擦阻尼等非线性因素对组合部件的振动响应有重要的影响。为了提高螺纹连接构件仿真模型的计算精度，需要准确地表征螺纹连接的接触状态，本文尝试采用薄层单元对螺纹接触状态进行模拟，并以模态试验的数据作为观测值，结合Nastran优化设计模块，对薄层单元的材料参数进行识别。结果表明无论螺纹连接处在黏滞、微滑移、宏滑移何种接触状态，参数识别后的薄层单元模型均可以较好地表征螺纹接触状态。得出以下主要结论：

1) 对于螺纹管结构，薄层单元建模的计算结果与传统建模方式进行比较，模态频率最大仿真误差从26.66%下降到1.35%. 将其应用于弹引螺纹连接结构中，模态频率最大仿真误差从4.71%下降到-0.64%，表明薄层单元模型可以有效地提高仿真计算精度。

2) 建立了基于试验结果对薄层单元材料参数识别的方法，识别后的薄层单元模型可以准确、合理地描述试验现象。

3) 薄层单元厚度选择对材料参数的识别精度有重要的影响。当薄层单元厚度与两倍的齿高相当时，参数的识别精度最高。