基于灰色关联度的两级实时航迹关联算法

靳冰洋， 刘峥， 秦基凯

(西安电子科技大学 雷达信号处理国家重点实验室， 陕西 西安 710071)

0 引言

弹载平台下多模复合导引头因其良好的抗干扰性能引起了相关学者的广泛关注[1-2]。分布式多传感器信息融合系统作为多模复合导引头数据处理的一种典型结构，具有结构简单、抗毁性好的特点，成为复合导引头数据融合处理的主要方式[3-5]，航迹关联作为分布式多传感器信息融合系统中的关键一步，用来判断各传感器的航迹是否属于同一目标[6]，其判别性能直接影响整个信息融合系统的性能。末制导阶段，导弹在对目标进行跟踪打击过程中当目标航迹之间存在交叉时易出现航迹关联错误；同时，由于目标释放的诱饵干扰，使得某些传感器观测数据相对目标真实位置产生严重偏移，进一步加剧了航迹关联处理的复杂性。

航迹关联算法主要有基于统计和基于模糊数学的方法。基于统计算法是以两两航迹状态估计的差值作为统计量[7]建立假设，以给定概率来判断航迹是否关联。这种方法较简便，易于工程实现，在稀疏目标且航迹无交叉环境下关联成功率较高，但在复杂环境下易发生关联错误[8-9]。基于模糊数学的算法通过选择或设计关联隶属度，计算两两航迹的隶属值来确定航迹是否关联。这种方法在密集目标环境下、航迹交叉分叉等场合可有效提高关联正确率，但是算法复杂，不易于工程实现[9-10]。航迹整体态势和航迹间的相似度对航迹关联判决至关重要[11]，而基于统计和基于模糊数学的航迹关联算法大多没有考虑航迹整体态势和航迹间形状的相似性对航迹关联判决的影响。基于灰色关联度的航迹关联算法从航迹的整体态势和航迹相似性出发进行航迹关联，且算法简便，运算时所需存储空间小，易于工程实现[12-13]。但目前基于灰色关联度的算法过分依赖灰色系统理论中的灰色关联度计算方法，未能与航迹关联实质结合，这是该方法实际应用情况中存在的问题。

本文论述了传统灰色航迹关联算法并分析了其不足，然后将灰色关联度计算与航迹关联问题相结合进行修正，提出一种两级航迹关联判决方法。仿真实验结果表明，本文算法在航迹交叉及干扰存在的复杂情况下航迹关联正确率高，算法较简单，可应用于现有弹载平台下。

1 灰色关联分析法

1.1 灰色航迹关联原理

航迹关联中，灰色关联度所指的关联性是两两航迹间的整体接近程度，两航迹整体接近程度越高，则航迹整体态势和相似性越高，灰色关联度越大[14]。灰色航迹关联算法大多采用经典且与航迹关联问题较符合的邓氏灰色关联度计算方法[11-12,15-16]。在航迹关联中航迹数列之间的相对关系对关联至关重要，而灰色系统理论中的灰色关联度仅度量序列几何关系的相似性，采用数据标准化将数据序列转化为数量级相似的无量纲数据，不关心数据列之间的相对关系，因此在计算航迹灰色关联度时不进行数据标准化[12]。

假设1：传感器1的航迹i和传感器2的航迹j源于同一目标；

假设2：传感器1的航迹i和传感器2的航迹j源于不同目标。

灰色航迹关联算法的航迹关联判决处理步骤如下：

1) 计算k时刻参考序列xi(k)与比较序列xj(k)的灰色关联系数：

(1)

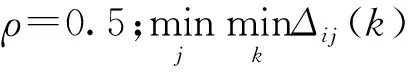
2) 计算参考序列Xi与比较序列Xj的灰色关联度：

(2)

3) 利用关联度γ与关联阈值门限进行比较，进行航迹的关联判决。

上述计算过程得到的灰色关联系数ξij(k)具有不可交换性，即在交换关系后得到的灰色关联系数不相等，造成在各传感器存在非共同观测目标情况下航迹关联错误明显上升。为解决该问题，文献[12]提出修正灰色关联系数计算式：

(3)

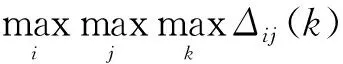
1.2 原有灰色航迹关联方法的不足

在实际应用过程中，原有灰色航迹关联算法的不足之处如下：

1) 原有灰色航迹关联算法在计算灰色关联系数ξij(k)时，仅片面地计算航迹间的两级或三级最大差和最小差，未能与航迹关联具体问题相结合。在航迹关联中，两级或三级最大差和最小差的取值应该具有一定范围，不能无限制地取值，否则会造成严重的关联错误问题。

例如，传感器1和传感器2都只有一条航迹且不关联，若按照原有方法计算灰色关联度γ，由(1)式和(3)式可知两级或三级最大差和最小差的差值服从的分布为

(4)

2)ρ值选择困难。原有方法通过反复的仿真实验确定合适的ρ值，这种确定ρ的方法对数据具有针对性，实际中由于目标机动的随机性，在固定ρ值情况下会使灰色关联度起伏变化较大，使得航迹关联性能变差，同时也会造成关联阈值设置困难。

3) 由灰色关联度的计算过程可知，灰色关联度γ是一个过程积累值，它与每个时刻的灰色关联系数ξij(k)有关，短时间周期内ξij(k)值的变化对γ值影响不明显，造成原有方法在出现航迹引偏干扰时关联错误。当航迹关联前期各航迹以及关联情况正常情况下，当后期目标释放干扰造成传感器观测数据相对目标位置发生严重偏移时，航迹灰色关联度γ会在较长一段时间后才可能低于关联阈值，产生不关联判决，此时已经造成严重的航迹关联错误。

2 算法描述

为提高弹载平台下复杂航迹情况的关联正确率，本文在改进原有灰色关联度计算基础上，提出一种基于灰色关联度的两级实时航迹关联算法。

2.1 第一级航迹关联判别

第一级航迹关联通过对航迹的整体态势和相似性进行比较进行航迹粗关联，以减少实际工程应用中的计算量，提高数据处理效率。

在紧密结合航迹关联处理本质的基础上，对灰色关联度计算进行修正。k时刻传感器1航迹xi(k)与传感器2航迹xj(k)的灰色关联系数计算公式如(5)式所示：

(5)

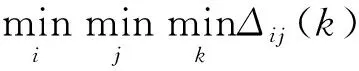
(6)

式中：Gc为门限系数，一般Gc∈[5,10]，可判定两条航迹存在的关联可能，Gc太小会出现漏关联，太大会造成错误关联。

(6)式满足时计算灰色关联系数ξij(k)，不满足时灰色关联度γ为0，继续与下一条航迹进行关联判断。

在(5)式中ρ值为

(7)

当Δij(k)值变大时，ρ值减小，ξij(k)值减小，表明k时刻两航迹的整体态势和相似度差；当Δij(k)值变小时，ρ值增大，ξij(k)值增大，表明k时刻两航迹的整体态势和相似度好。这种变ρ值的方法进一步提高了航迹关联正确率，并解决了仿真实验确定的ρ值在目标机动性影响下航迹关联效果差的问题，可以更好地反映各个时刻航迹间的关系，使航迹间灰色关联度更加稳定。

在得到灰色关联系数序列ξij={ξij(k),k=1,2,…,l}后，计算两航迹的灰色关联度γ. 由于在整个航迹关联过程中每个时刻的航迹数据信息对关联判决的影响程度是相同的，故灰色关联度为

(8)

(9)

k时刻传感器1所有航迹与传感器2所有航迹的平均灰色关联度γij(k)可构成一个矩阵，称为灰色关联矩阵，即

(10)

式中：

(11)

e0为关联判别门限，e0∈[0.5,1)。

灰色关联矩阵Γ中不为0元素所对应的航迹对为第一级关联判别为关联的航迹对，元素值为0时对应的航迹之间不关联。

2.2 第二级航迹关联判别

第二级航迹关联判别是对第一级判别为关联的航迹对进行再一次的局部关联检验，利用当前N0个时刻航迹的局部关联情况，来弥补灰色关联度γij(k)对中途出现的航迹异常、无法做出及时反应的不足，N0为局部检测长度，一般N0∈[5，10]。

由于灰色关联系数ξij(k)局部稳定性较差，特别是密集目标情况下起伏较大，不能用于航迹的局部关联判别，这里以归一化位置差值的绝对值uij(k)为检测统计量。

(12)

(13)

(14)

(15)

在第二级关联判决中设置航迹脱离质量Dij(k)，其值大小为两航迹当前N0(N0为局部检测长度，一般N0∈[5,10])个点迹满足(16)式的点迹对个数。

uij(l)>e1,l∈[k-N0+1,k]，

(16)

式中：e1为每时刻的关联判别门限值。当Dij(k)>K时，判定为两航迹不关联，同时灰色关联矩阵Γ中εij置为0.K为第二级航迹关联判决门限常数，K的取值为[μ·N0]，[ · ]代表取整，μ>0.5.

2.3 最终航迹关联判决准则

经两级航迹关联处理后，最终航迹关联判决采用最大值准则，该准则简便、易于实现，可减轻弹载平台下的运算压力，同时也可实现良好的航迹关联判别效果。

根据两级关联处理后得到的灰色关联矩阵Γ，判定矩阵中εij>0的最大值所对应的航迹对为关联航迹对，然后将灰色关联矩阵所对应的行和列非0值置为0，按照该方法逐次进行航迹关联判决，直至灰色关联矩阵的值全部为0.

当M(M>2)个传感器对公共观测区域进行航迹关联时，有航迹号集合Us={1,2,…,ns}，s=1,2,…,M. 构造全局统计量αi1i2…iM(k)，

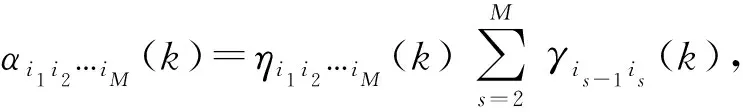
(17)

式中：γis-1is(k)为Us-1传感器航迹is-1与Us传感器航迹is的平均灰色关联度。

(18)

与两传感器类似，采用最大值判别准则，

maxαi1i2…iM(k),

(19)

得到k时刻的多维灰色关联矩阵后，选择αi1i2…iM(k)>0的最大航迹序列为关联序列，并将对应的序列号航迹的α值置0，然后选取最大值序列，依次循环，直至α值全部为0.

最后输出关联航迹对数据，进入下一时刻航迹关联判断。

2.4 算法复杂度分析

整个算法处理可分为3部分：第一级航迹关联判别、第二级航迹关联判别、关联航迹对选择输出。

以两传感器为例分析算法复杂度。在第一级航迹关联判别中，灰色关联系数和灰色关联度的计算和比较过程可以通过嵌套的循环实现，利用大O表示法计算事件复杂度为O(n1·n2)；第二级关联判别对N0点局部情况进行判别，时间复杂度为O(1)；关联航迹对输出阶段，仅通过循环查找最值，时间复杂度为O(n1·n2)。在具体工程实现时可以采用适合的编程方法，进一步提高运算效率。

在空间复杂度方面，灰色关联度的计算可以通过一个变量不断累加求平均，因此不需要存储整个航迹的所有数据信息；其他需要存储的数据也仅为灰色关联矩阵数据和N0个周期内的航迹数据信息，因此本文算法占用存储空间较小。

在弹载平台下多模复合导引头末制导阶段，导弹对目标进行跟踪打击时目标个数较少，一般在3个目标左右，因此算法在时间复杂度和空间复杂度上可满足现有平台要求。

3 仿真实验

3.1 仿真环境

为方便讨论问题，这里以双模复合导引头弹体坐标系下的观测航向角为测试数据进行算法性能验证；仿真进行50次蒙特卡洛实验，对本文所提基于灰色关联度的两级实时航迹关联算法与灰色航迹关联算法[11]和经典航迹关联算法中的加权法[9]、序贯航迹关联算法[9]进行性能比较。

假设传感器1与传感器2的观测角误差分别服从均值为0、均方差分别为σ1和σ2的高斯分布；灰色关联门限设为0.65；灰色航迹关联法的分辨系数ρ为0.5. 在二维平面Oxy上存在3个目标，目标1位置为二维平面原点O，目标2和目标3在二维平面不同坐标位置。在Oxy坐标系下，导弹初始运动角度为0°，目标1初始运动角度为-150°，目标2初始运动角度为-210°，目标3初始运动角度为-90°.

在3种环境下对本文所提算法进行性能验证和评估，各环境下两个传感器观测误差均方差和各目标状态信息如表1所示。

表1 传感器观测误差均方差及目标状态信息

下面根据表1对各环境下目标和干扰情况做进一步说明。环境1时目标无干扰释放，两传感器对3个目标正常观测跟踪，在观测过程中，由于目标运动使得观测航迹存在交叉。环境2在环境1的基础上，目标1和目标3释放干扰；目标1在运动过程中第9 s时释放诱饵干扰，在诱饵弹释放后，使得传感器2的观测数据相对目标1位置发生偏移，对传感器1不产生影响；目标3释放干扰，使得传感器2在整个过程中无法观测到目标3，对传感器1不产生影响。环境3与环境1相似，目标无干扰释放，两传感器对3个目标正常观测跟踪，但传感器观测误差均方差及目标状态与环境1不同。图1～图3分别为3种测试环境下其中一次随机仿真数据。

图1 环境1下算法测试数据Fig.1 Test data used in Environment 1

图2 环境2下算法测试数据Fig.2 Test data used in Environment 2

3.2 仿真结果分析

图3 环境3下算法测试数据Fig.3 Test data used in Environment 3

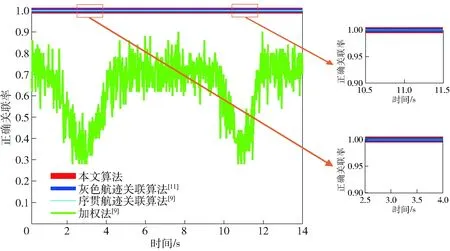
图4 环境1下各算法正确关联率Fig.4 Accurate correlation rates of 4 algorithms in Environment 1

在环境2下，当目标释放干扰使航迹发生偏移时，利用灰色航迹关联算法和序贯航迹并联算法进行航迹关联会出现关联错误。图5～图7为环境2下本文所提算法在关联过程中，传感器1、航迹与传感器2、各航迹间的灰色关联度；图8～图10为环境2下传感器1、航迹与传感器2、各航迹间由灰色航迹关联法计算所得的灰色关联度。由图5～图10可看出当航迹情况复杂时，灰色航迹关联算法会出现关联错误。

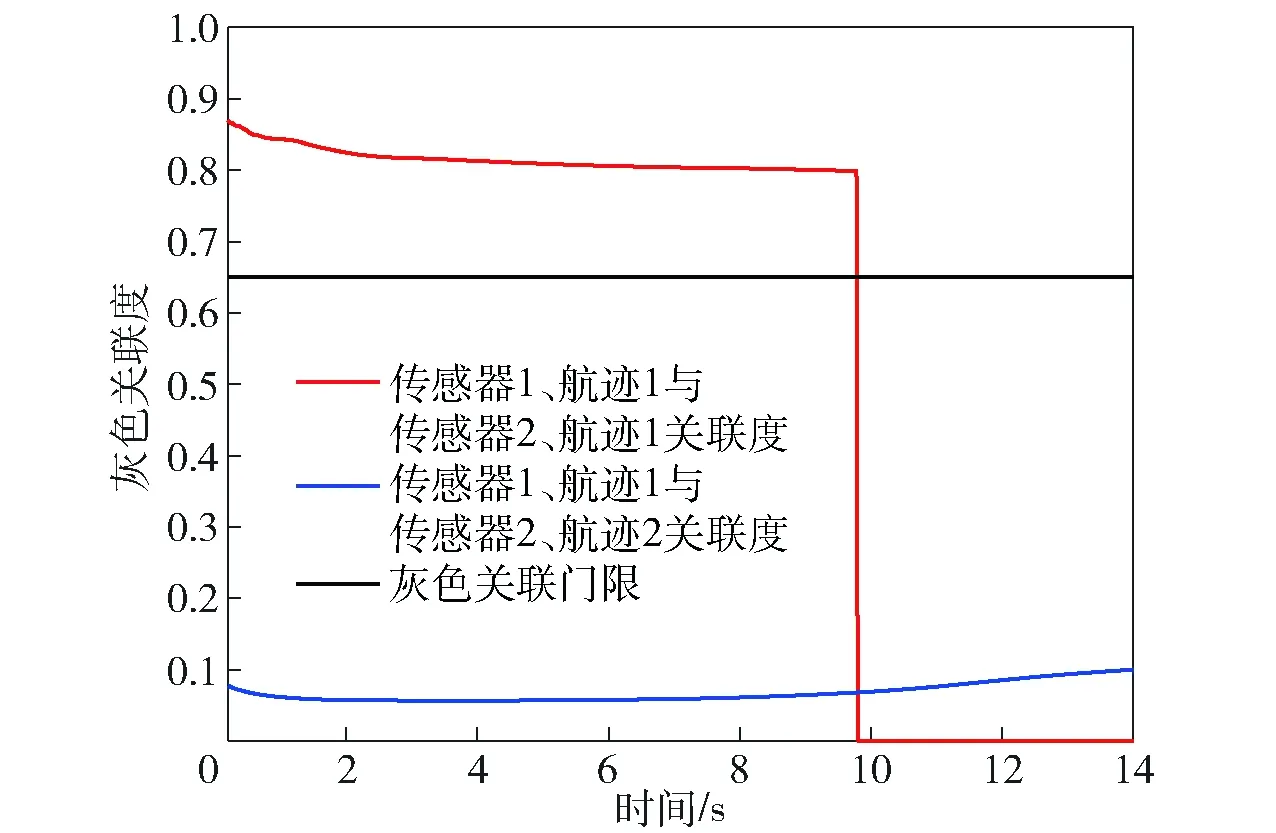
图5 环境2下传感器1、航迹1与传感器2、各航迹两级灰色关联度Fig.5 Two-stage gray correlation degrees between Track 1 observed by Sensor 1 and tracks observed by Sensor 2 in Environment 2

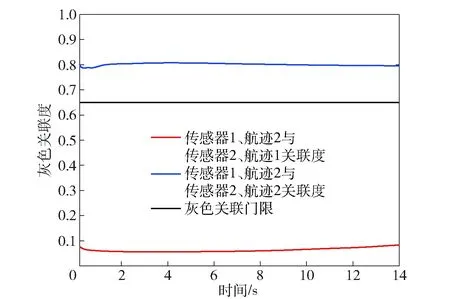
图6 环境2下传感器1、航迹2与传感器2、各航迹两级灰色关联度Fig.6 Two-stage gray correlation degrees between Track 2 observed by Sensor 1 and tracks observed by Sensor 2 in Environment 2

图7 环境2下传感器1、航迹3与传感器2、各航迹两级灰色关联度Fig.7 Two-stage gray correlation degrees between Track 3 observed by Sensor 1 and tracks observed by Sensor 2 in Environment 2

图8 环境2下传感器1、航迹1与传感器2、各航迹灰色关联度Fig.8 Gray correlation degrees between Track 1 observed by Sensor 1 and tracks observed by Sensor 2 in Environment 2

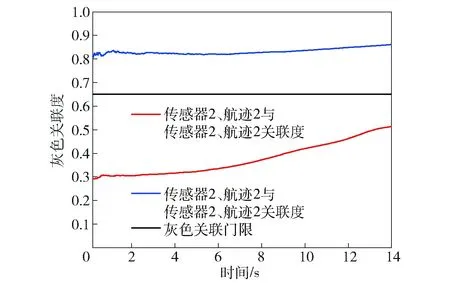
图9 环境2下传感器1航迹2与传感器2各航迹灰色关联度Fig.9 Gray correlation degrees between Track 1 observed by Sensor 1 and tracks observed by Sensor 2 in Environment 2

图10 环境2下传感器1、航迹3与传感器2、各航迹灰色关联度Fig.10 Gray correlation degrees between Track 3 observed by Sensor 1 and tracks observed by Sensor 2 in Environment 2

对比图5和图8可以看出：关联过程中航迹关联对某条航迹因干扰发生偏移时，灰色航迹关联算法不能及时做出不关联判决，灰色关联度始终大于关联门限，造成关联错误；而本文提出的算法在出现该情况时，可迅速做出不关联判决。图6和图9为两种算法关联正确的情况，但本文提出的算法使得不关联航迹间的灰色关联度更低，降低了出现误判的概率，关联航迹与不关联航迹的灰色关联度差值更大。对比图7和图10，进一步证明了灰色航迹关联算法的关联度计算方式对航迹关联判决不具有普遍适用性，传感器1、航迹3与传感器2、航迹2在一段时间内的关联度大于关联门限，而本文所提算法的关联度计算值低于关联门限，且与门限值有一定的差距。

表2为环境2下50次蒙特卡洛实验测得本文所提算法和序贯航迹关联算法在干扰航迹发生偏移后，两种方法做出不关联判决所用反应时间(反应时间=不关联判决时刻-干扰出现时刻)的平均值。

表2 平均反应时间

由表2数据可知：环境2下目标1释放干扰后序贯航迹关联算法存在和灰色航迹关联法类似的问题，当航迹因干扰发生偏移时，序贯航迹关联算法不能尽快做出不关联判决，出现航迹关联错误，而本文算法可以在较短时间内做出正确的判决。图11为环境2下本文算法与序贯航迹关联算法航迹正确关联率。由图11可知，序贯航迹关联算法在干扰释放后一段时间内发生关联错误，而本文算法依旧正确进行航迹关联判决(注：航迹关联过程中当某条航迹因干扰逐渐偏移时，在初期极短的一段时间内无法做出不关联判决，需要一段积累时间，为避免引起错误引导，图11忽略了这一段积累时间的影响)，从而表明本文所提方法优于序贯航迹关联算法。

图11 环境2下算法正确关联率Fig.11 Accurate correlation rates of algorithms in Environment 2

在环境3下，两传感器的观测角误差均方差相比环境1和环境2较大。环境3下4种算法的航迹正确关联率如图12所示。

图12 环境3下各算法正确关联率Fig.12 Accurate correlation rates of 4 algorithms in Environment 3

由图12可知，在传感器观测角误差较大的情况下，利用本文所提算法进行航迹关联判决的正确率依旧较高，表明本文算法适用于传感器观测角均方差较大情况下的航迹关联处理。

以上仿真结果表明，本文所提算法利用航迹整体态势和航迹的局部特性进行航迹关联判决具有较好的航迹关联效果，在航迹交叉和干扰情况下依然可以正确地进行航迹关联，可应对更为复杂的航迹关联情况，并且本文算法对传感器不同观测误差方差下的航迹关联处理具有普遍适用性。

4 结论

本文针对目标航迹存在交叉或干扰时弹载平台下多模复合导引头原有航迹关联算法易出现航迹关联错误的问题，在原有灰色航迹关联算法的基础上提出了一种基于灰色关联度的两级实时航迹关联算法。通过仿真实验可得到如下结论：

1)所提算法将灰色关联度计算与航迹关联紧密结合，并对灰色关联度计算进一步修正，通过两级航迹关联判决得到航迹间的最终灰色关联度，最终以最大值准则得到关联航迹对，该过程对航迹关联处理正确有效。

2)本文算法在航迹交叉情况下关联正确率明显优于加权法，在无关联对航迹或航迹中途发生偏移干扰时，优于灰色航迹关联算法和序贯航迹关联算法，提高了复杂环境下的航迹关联性能。

3)本文算法对传感器不同观测误差方差下的航迹关联处理具有普遍适用性。

4)本文所提算法运算量较小，编程实现时需要的存储空间有限，可以满足现有弹载平台下对实时性和存储性能的要求。