“四问法”在初中数学中列方程解应用题的有效教学实践

陈旭旋

【摘要】  数学应用题难教、学生难学的现象一直困扰着我们教师和学生，在实际教学中教师都清楚“如何准确找到等量关系列方程”是教学的难点，教师们也做了各种教学研究，想方设法引导学生突破这个难点，但实际教学效果一般，学生大多还是不会找，另外，学生一见实际问题就“一个头两个大”，要么直接放弃，要么做了半天依旧不知如何下手。

【关键词】  初中数学 列方程解应用题 有效教学实践

【中图分类号】  G633.6            【文献标识码】  A     【文章编号】  1992-7711（2020）23-080-02

笔者在近年的“实际问题”教学实践中，借助四个问题追问法引导学生寻找等量关系，取得很好的效果，尤其对于七年级刚接触列方程解一元一次方程的学生，效果更加明显，应用题的测试成绩高于其他班级的2倍以上。下面笔者就2019年12月参加教学能力大赛的获得第一名的《一元一次方程与实际问题》这节课进行部分课堂实录整理，谈谈如何用“四问法”有效提高学生准确列方程解应用题的教学效果，从而提高学生的数学建模能力，与同行们共勉。

一、情境引入，引出课题

【情境1】

教师：孩子们，你们从图片看到了什么？

学生：春运

教师：春运又让你想到什么？

学生1：想回家过年

学生2：买票难

……

教师：嗯，有句歌词：“有钱没钱，回家过年……”但是票却不容易购买，现在大多可以网上提前购票，2020年的春运（春运指当年的腊月十五或十六开始到第二年的正月廿五结束。）从双十二那天开始也拉开了抢票的序幕。下面请同学们看大屏幕上的两张火车票：

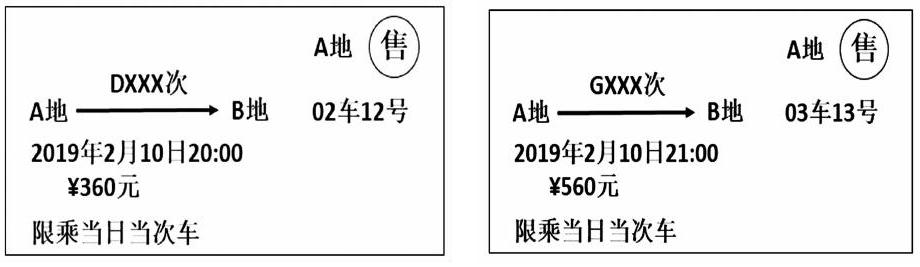
【情境2】以下是两张不同类型火车的车票：（“D×××次”表示动车，“G×××次”表示高铁）：

已知该动车和高铁的平均速度分别为200km/h，300km/h，如果两车均按车票信息准时出发，且同时到达终点，求A，B两地之间的距离。

教师：请同学们独立完成情境问题。

学生独立完成，教师巡视。

二、例题剖析，提炼方法

以【情境2】作为例题

教师：请同学们停下来，从刚刚巡视发现大部分同学无法动笔，能谈谈你不会做的原因是什么吗？

学生1：看不懂题目，不会找已知量、未知量（原因：阅读理解能力差）

学生2：不知道已知量和未知量有什么联系，好乱，完全无思路，不知从何下手（原因：数量关系复杂，有隐蔽的数量关系，路程=速度×时间，还有题目中显性的复杂数量关系，学生思维无序）

学生3：不知怎么设未知数（原因：多个未知数，未知数选择的灵活性）……

教師：好，大家说的正是我们列方程解应用题“因何而难”的原因：（1）题目文字多，一看就怕;（2）数量关系复杂：既有隐藏的数量关系如行程问题中的路程、速度、时间三者的关系，如利润问题涉及进价、售价、标价、利润率等之间的数量关系;又有题目所给的各种显性数量关系;（3）用代数式表示数量关系能力差，如何用代数式来表示各个已知量和未知量呢，无从下手（4）题目中未知量往往有多个，不知选择哪个来设未知数。

教师：下面老师带领大家用“四步追问法”克服这些困难，轻松建立一元一次方程（数学模型）解决实际问题。

教师：首先，我们一起来看看，你能从两张火车票获取什么信息？

学生4：路程相同，都是从A地到B地。

学生5：出发时间不同，动车是20：00，高铁是21：00，晚一个小时。

学生6：两张票都是从A地购买，价格不同。

……

教师：票面信息可真多呀，但是有些是题目中有用的信息，有些是非数学元素的干扰信息，我们需要剔除掉，下面请同学思考：

问题1：例题中共有几个量？哪些是已知量？哪些是未知量？需要求什么？请同学们一句一句阅读题目，用圈划方法获取信息。

学生：已知量有动车的平均速度200km/h，高铁的平均速度300km/h，动车和高铁出发的时间。

学生：未知量有A地到B地的路程，动车行驶的时间，高铁行驶的时间。

教师根据学生的回答进行板书如下：

问题2：问题1中各个量之间有怎样的数量关系？（一隐性二显性关系）

教师：路程、时间、速度有什么数量关系？

学生：路程=速度*时间①（可变形）

教师板书并提问：这个数量关系是题目告诉我们的吗？

学生：不是，是行程问题中的公式。

教师：很好，这类公式如行程问题中路程=速度*时间，工程问题中工作量=工作效率*工作时间等属于应用题中的隐性数量关系，需要我们平时掌握的。

教师：题目中明确告诉我们的，有哪些数量关系？

学生7：动车从A到B地所用的时间比高铁从A到B地所用的时间多1小时

学生8：动车行驶的路程和高铁行驶的路程相同，都是从A地到B地。

教师根据学生的回答进行如下右边的板书：

问题3：如何选择未知量设未知数？其他各量又怎样表示？

教师：现在题目中有四个未知量，选择哪个未知量设未知数呢？一般我们习惯问什么设什么，所以我们设A、B两地间的距离为xkm，那其他未知量如何用未知数x来表示呢？

教师根据学生回答进行如下板书：

问题4：你能用表格的形式对以上分析进行直观化展示吗？

教师：对于刚才我们的分析板书看起来有些凌乱，你能否利用表格将这些量进行分析并列出方程？哪位同学尝试以下。

学生9展示如下：

教师：你怎么想到的？

学生9：刚才数量关系①③都用来表示各个未知量了，所以只能选择数量关系②时间差作为等量关系列出方程。

教师：分析很到位，一个应用题中有多个数量关系时，如果你选择其他的数量关系来表示未知量，那么就不能再作为等量关系来列方程了，否则就会解不出来，课后同学们可以尝试一下就明白了。這也是老师为什么要求同学们一定要先找到所有的数量关系，然后再根据这些数量关系来设未知数列方程，可以将我们无序的思维有序化，这样解应用题时就能清晰知道用哪个等量关系来列方程了。明白了吗？

学生：明白了。

教师：那老师来考考你们。例题中若选择动车的时间这个未知量来设未知数x，你会用含x的代数式表示其他未知量并列出方程吗？请同学动手尝试一下。

学生独立完成，教师巡视

学生展示如下：

教师：很棒，我们来对比这两种设法列方程的优缺点？谈谈你更喜欢哪一种？

学生：……

教师：很好，通过刚才例题的学习，我们回过头来总结一下，我们是怎么找到等量关系列出方程的？

师生共同完成：先读题找已知量未知量，找全数量关系，再用含未知数的代数式表示各个未知量，用表格直观化根据数量关系列出方程了。

教师：老师把这个过程称之为“四步追问法”，简称“四问法”，也就是我们在解应用题的时候不要急于设未知数，直接就列方程，而是先进行自我四问，在草稿纸上分析数量关系，这对于我们刚学应用题时至关重要，可以避免审题时遗漏条件，弄错数量关系列出方程。另外，我们在借助表格对数量关系进行分析时，我们习惯把各个考查对象放表格竖列，把各个数量放在横列。

……

“问题1”是一个去情境化实现数学抽象的过程，从复杂的实际情境中剔除无效信息的干扰，提取有效信息，将学生的思维引向对“已知量”“未知量”的分析，明确问题目标，为进一步分析数量关系奠定基础;

“问题2”是通过问题引导，完成隐性的数量关系显性化、并找到情境中的显性的所有数量关系的程序，为将各量关系从文字语言向符号语言转换奠定基础;

“问题3”既是为了避免学生在将文字语言转化符号语言的过程中往往会因为思维的随意性而漏掉重要的数学条件，所以通过问题引领的方式，让学生将无序思维有序化又是为了在设未知数x并用含x的代数式表示其他各个未知量的过程中，紧紧抓住各量之间的数量关系，让学生深刻体会关系的桥梁作用;

“问题4”是在分析了各个量以及其中的各种数量关系的基础上，再去利用表格进行分析，再次强化对各量之间关系的分析，使得各种抽象关系直观化。表格或图是随着数量关系的分析自然生成的，这是一种加深学生理解数量关系的辅助手段，和以往直接呈现表格分析数量关系的逻辑思维是相反的。通过这四个问题的引导，学生在建立数学模型解决实际问题过程中，能将无序思维有序化，又将数量关系可视化，再通过一题多设、一题多列的比较，更有利于学生加深对数量关系分析的理解，积累数学经验，并强化按照步骤分析解决问题的思维方式和能力。

“四问法”建立数学模型解决实际问题，在笔者实际教学实践中，尤其七年级学生刚刚接触一元一次方程解实际问题，能准确列出方程的效果明显提高，学生也对应用题的心理障碍大大减少，对后续实际问题的继续学习起到至关重要的作用。