基于可靠性分析的电梯制动器设计方案优化方法

欧阳惠卿，舒文华，薛季爱

(上海市特种设备监督检验技术研究院，上海 200062)

0 引言

随着我国经济的高速发展和城市化的快速推进，电梯已经成为人们日常出行必不可少的垂直交通工具。截至2019年底，我国在用电梯数量已达709.75万台[1]。但是，电梯事故偶有发生，往往造成严重的人身伤亡或恶劣的社会影响。其中，由于制动器失效而造成的轿厢蹲底、冲顶、在开门区域发生意外移动导致人员伤亡的事故占了较大的比例。因此，原国家质检总局对制动器的安全性开展了多次专项整治[2]，并通过修订检验规范和标准以提高制动器的技术要求和安全水平[3-4]。因此电梯制动器也是电梯行业的重点研究内容之一。吴昊[5]等人基于检验工作总结，分析了制动器制动力不足、电气问题等常见故障，并针对性地提出了检验对策。许海刚[6]对电梯鼓式制动器故障模式及其机理展开了深入研究，建立了制动力矩不足、制动响应时间超时、释放响应时间超时、制动器不抱闸和制动器不松闸等主要故障模式的故障树。欧阳惠卿等人[7]基于有限元仿真的电梯紧急制停时闸瓦温度变化和高温失效进行了分析。张雨枫等人[8]对电梯盘式制动器可靠性进行了初步的分析，并提出了检验工作中的注意要点。

本文基于可靠性分析理论，以常见的电梯鼓式制动器为研究对象，通过结构和工作原理的分析，对“串-并联系统”和优化后的“并-串联系统”可靠性进行计算分析，并提出了鼓式制动器优化设计方案。

1 电梯制动器的基本原理

对于曳引电梯，由于轿厢和对重存在质量差，如果制动器失效，容易导致轿厢在开门状态下溜车，也容易发生轿厢蹲底、冲顶，制动器失效等严重的安全隐患。

鼓式制动器的结构如图1所示，主要由电磁装置、制动弹簧、制动臂、制动闸瓦4部分组成。制动弹簧提供制动时所需的压力，制动臂用于传递驱动力，制动闸瓦在制动时与制动轮相接触，产生制动摩擦力，电磁装置提供用于释放的电磁力。

1—释放手柄；2—电磁装置；3—顶杆；4—微动开关；5—制动弹簧螺杆；6—制动弹簧；7—垫圈；8—螺母；9—制动轮；10—制动闸瓦；11—连接螺钉；12—制动臂；13—轴销。图1 鼓式制动器结构图

GB 7588-2003《电梯制造与安装安全规范》对电梯制动系统的性能提出了一系列的要求[3]。当轿厢载有125%额定载荷并以额定速度向下运行时，操作制动器应能使曳引机停止运转。所有参与向制动轮或盘施加制动力的制动器机械部件应分两组装设。如果一组部件不起作用，应仍有足够的制动力使载有额定载荷以额定速度下行的轿厢减速下行。

2 电梯制动器的可靠性计算

2.1 电梯制动器失效和可靠性分析

根据可靠性分析理论，系统是由若干彼此相互协调工作的零部件、子系统组成，以完成某一特定功能的综合体。构成机械系统的可靠性取决于以下两个因素：1) 机械零部件本身的可靠度，即组成系统的各个零部件完成所需功能的能力；2) 机械零部件系统的组合方式。

本文的研究对象是如图1所示的常见电梯鼓式制动器，制动器可以看成一个机械系统。基于文献[6]对制动器失效故障及机理的分析，制动器制动力矩不足、制动响应时间超时、释放响应时间超时、制动器不抱闸和制动器不松闸等形式的失效主要与构成鼓式制动器的电磁线圈、电磁铁芯、制动弹簧、制动闸瓦等零部件的失效有关。

2.2 电梯制动器的可靠性框图

为了简化模型，基于文献[6]的研究，本文只考虑将对鼓式制动器失效影响较大的主要部件纳入可靠性分析，即：电磁线圈、电磁铁芯、制动弹簧、制动闸瓦。

根据GB 7588-2003的规定，所有参与向制动轮或盘施加制动力的制动器机械部件应分两组装设。如果一组部件不起作用，应仍有足够的制动力使载有额定载荷以额定速度下行的轿厢减速下行。电磁线圈的铁芯被视为机械部件，而线圈则不是。

目前电梯的制动器如图1所示，采用2个独立制动臂，每个制动臂连接1个制动弹簧、1个闸瓦、1个铁芯，2个制动臂的铁芯共用1个电磁线圈。

制动过程为：电磁线圈一旦失电，制动臂在制动弹簧的作用下，带动闸瓦压紧制动轮，从而实现制动。

松闸过程为：电磁线圈通电，电磁力推动铁芯和顶杆，克服制动弹簧力，使制动臂张开，制动闸瓦脱离制动轮，从而实现松闸。

每边的制动臂及铁芯、弹簧、闸瓦共同工作才能实现制动和松闸功能。2个制动臂相互独立，但是2个制动臂共用1个电磁线圈。根据制动器的结构和工作原理，可以绘制出如图2所示的可靠性框图。图2中，如果制动器能可靠制动，则要求线圈、铁芯、弹簧、闸瓦均能正常工作。由于铁芯、弹簧、闸瓦属于机械部件，存在冗余，因此只要其中某单边的铁芯、弹簧、闸瓦都正常，加上线圈正常，制动器即可满足要求。这样，单边的铁芯、弹簧、闸瓦首先构成了一个串联系统，然后与另一边的铁芯、弹簧、闸瓦构成的串联系统，组成了一个并联系统。这个并联系统最后与线圈串联，组成了整个制动器的可靠性框图，本文将这种常见制动器的可靠性框图定义为串-并联系统。

图2 常见制动器的可靠性框图(串-并联系统)

2.3 常见制动器(串-并联系统)的可靠性计算

1) 可靠度定义

可靠度(reliability)是产品在规定的条件下和规定的时间内完成规定功能的概率[9]。可靠度是时间的函数，一般用R(t)表示，可表达为：

R(t)=P(E)=P(T≥t), 0≤t≤

(1)

条件T≥t就是产品的寿命超过规定时间t，即在时间t之内产品完成规定功能。根据定义有：

0≤R(t)≤1,R(0)=1,R(+)=0

(2)

2) 串-并联系统的可靠性计算

本节将重点计算如图2所示的常见制动器的可靠性框图，本文将这种先串联后并联的方式称为“串-并联系统”。为了简便计算过程，本文后续章节计算过程中用R代替R(t)。

设铁芯、弹簧、闸瓦和线圈的可靠度分别为：R1、R2、R3和R4，且每边的铁芯、弹簧、闸瓦具有相同的可靠度。

根据串联系统可靠度的计算规则，铁芯、弹簧、闸瓦串联系统的可靠度为：

(3)

根据并联系统可靠度的计算规则，将2个铁芯、弹簧、闸瓦串联系统并联起来后，并联部分的可靠度为：

R123并=1-(1-R123)2=1-(1-R1R2R3)2

(4)

根据串联系统可靠度的计算规则，将上述并联系统与电磁线圈串联起来，就组成了整个制动系统，其可靠度为：

Rs1=R4·R123并=R4[1-(1-R123)2]=R4-R4(1-R1R2R3)2

(5)

3 优化后的“并-串联系统”可靠性计算

机械系统的可靠性不仅取决于机械零部件本身的可靠度，也取决于机械零部件组合成系统的组合方式。在不增加和减少零部件的基础上，可以将如图2所示的结构优化，调整为图3所示的可靠性框图，本文将这种先并联后串联的方式称为“并-串联系统”。本节接下来将根据可靠性理论对优化后的“并-串联”制动器的可靠性进行计算。

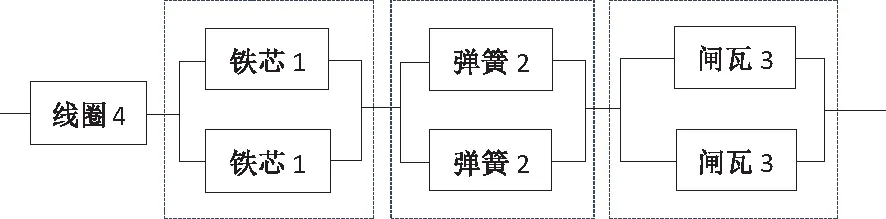
图3 优化后制动器的可靠性框图(并-串联系统)

同样，设铁芯、弹簧、闸瓦和线圈的可靠度分别为：R1、R2、R3和R4,

则2个铁芯并联的可靠度为：

R1并=1-(1-R1)2

(6)

2个弹簧并联的可靠度为：

R2并=1-(1-R2)2

(7)

2个闸瓦并联的可靠度为：

R3并=1-(1-R3)2

(8)

上述3个并联系统串联上电磁线圈后，整个系统的可靠度为：

Rs2=R4·R1并·R2并·R3并=

R4[1-(1-R1)2][1-(1-R2)2][1-(1-R3)2]

(9)

4 两种不同组合方式可靠性的比较

由上述分析可知，图2所示的“串-并联系统”和图3所示的“并-串联系统”所采用的零部件类型、数量均没有发生变化，但是组合方式发生了变化，其整个系统的可靠性也明显发生了变化。

为了对比“串-并联系统”和“并-串联系统”的可靠性差异，本节将以一些具体算例进行比较。

假设任意时刻t，R1=R2=R3=R4=R，定义ΔRs=Rs2-Rs1，则Rs1、Rs2、ΔRs随着部件可靠度R(R∈[0,1])增加的变化如图4所示。显然，Rs1≤RS2，ΔRs≥0，即，“并-串联系统”的可靠性要优于“串-并联系统”。从图4还可看出，当零部件可靠度R∈(0.3,0.9)时，“并-串联系统”的可靠性优势比较明显。

图4 Rs1、Rs2、ΔRs随部件可靠度R(R∈[0,1])增加的变化

假设某时刻t，R1=R2=R3=R4=0.70，则有：

根据式(5)，串-并联系统的可靠度为

Rs1=R4-R4(1-R1R2R3)2=0.7-0.7×(1-0.73)2=0.397 845 7。

根据式(9)，并-串联系统的可靠度为

Rs2=R4[1-(1-R1)2][1-(1-R2)2][1-(1-R3)2]=

0.7×[1-(1-0.7)2]3=0.527 499 7。

而“并-串联系统”与“串-并联系统”的可靠度差为

显然，在上述条件下，相比“串-并联系统”，“并-串联系统”的可靠性有非常明显的优势。

5 结语

本文首先介绍了电梯鼓式制动器的基本原理，然后描述了其常见的失效模式。重点运用可靠性理论，对现有普遍的制动器设计方案，即“串-并联系统”的可靠性进行了推导计算。在不增加和减少制动器零部件的条件下，对制动器零部件的工作组合方式进行了优化，形成了新的“并-串联系统”。通过算例的计算结果表明，新的“并-串联系统”比现在普遍采用的“串-并联系统”具有更好的可靠性。

电梯制动器设计制造单位可以依据本文的研究结果，在不增加和减少现有零部件、不提高现有零部件本身可靠性水平的基础上，通过科学合理的设计，即通过改变调整零部件的组合方式，就可以提升整个系统的可靠性。也就是说，在不增加成本的基础上，可以通过优化设计提高产品的可靠性。