几何参数对S弯进气道气动特性的影响研究

王云飞，沈天荣，宁啸天，孟轩，袁化成，周正贵

(1. 南京航空航天大学 a. 能源与动力学院； b. 江苏省航空动力系统重点实验室，江苏 南京 210016；2. 沈阳飞机设计研究所，辽宁 沈阳 110035)

0 引言

随着高新技术的发展，现代一线装备已呈明显的无人化趋势。无人机自问世以来，就以独有的低成本、低损耗、零伤亡、可重复使用和高机动性等诸多优势受到越来越多国家的重视[1-5]。进气道作为推进系统的重要组成部分，其性能的优劣直接影响无人机的作战性能，因此对无人机进气道进行研究具有重要意义[6]。

S弯进气道作为一种典型的进气道形式，得到了广泛关注。其流场特征具有鲜明的特点，特有的 S 弯管形状，有两个方向不同的弯道，气流主流经过这两个弯道时，由于离心力的作用，使得进气道两个弯道的高压区和低压区的分布刚好相反[7]；同时在周向方向上附面层的存在，使得气体压力驱动气流产生二次旋流；两个弯道二次旋流的方向是相反的，因而在进气道的出口处产生独特的“对涡”结构[8]。国内对S弯进气道内的对涡和旋流及旋流的抑制也进行了大量研究[9-15]。近年来，随着对S弯进气道需求的增加，有关S弯进气道设计及流场控制等研究不断增加。谢旅荣[16]设计一种受总体约束的弹用S弯进气道,并进行了实验验证。靖建朋等对一种双S弯进气道进行了地面状态的试验研究，并对进气道的附面层抽吸进行了实验[17-19]。刘雷等对S弯进气道出口旋流畸变及埋入式进气道的设计优化及流场控制进行了广泛研究[20-23]。宁乐等对有无附面层吸入对S弯进气道流动特性的影响进行了研究[24]。为提高S弯进气道性能，张竞等基于大规模数值计算建立了一种S弯进气道的全自动优化方法[25]。

本文采用数值仿真方法对无人机S弯进气道进行了研究。首先对某无人机S弯进气道内流场结构进行了分析，研究中间截面及出口截面流场特征及出口参数。然后，对偏移距离和进气道的长度等几何参数对S弯进气道气动特性的影响进行了研究。

1 数值仿真方法

1.1 弯进气道基础构型

图1为某无人机用S弯进气道的基础构型(半模型)，飞行器前端至进气道出口全长约为4088mm，S弯入口至S弯出口长度为2 413mm，其中包括尾部200mm长度的等直段，出口圆截面半径为375mm，进气道入口为类三角形，内通道扩张比约为1.2530，中间截面中心相对入口底边向下偏移距离约为0.45L/D。出口圆壁面计算时再向后延长1m以隔绝出口压力边界条件的直接影响。

图1 S弯进气道基础构型(半模型)

1.2 网格及数值仿真方法

采用内外流一体化的计算方式，图2给出了外流场边界处的边界条件类型，包括压力远场、压力出口。入口上下及前方流场边界距离飞行器的距离为15倍飞行器长度尺寸。由于模型对称且计算条件无攻角和侧滑角，为了减小计算量采用半模型进行计算[26]，因此还需要引入对称面边界。

对上述内外流一体化构型进行结构化网格划分，其中飞行器表面网格以及飞行器前缘和唇口前缘网格如图3所示，总网格量约为520万。

图2 计算域与计算边界(半模型)

图3 计算网格(半模型)

仿真软件采用商业软件Fluent，求解三维定常N-S方程，若采用坐标变换：

ξ=ξYx,y,zY

ζ=ζYx,y,zY

N-S方程组表达为：

采用基于压力的耦合求解器，湍流模型选择基于RANS的综合能力较好的 SSTk-ω。切应力输运(shear stress transport, SST)格式的k-ω模型是由Menter提出的[27]。SST格式k-ω模型的特点是在近壁区内采用k-ω模型，在附面层边缘和自由剪切层采用k-ε模式，其间通过一个混合函数来过渡，通过系数叠加统一写成k-ω形式。由于有效地结合了k-ω模型的近壁特性和k-ε模型对自由流计算的优点，使得SST格式k-ω模型的应用范围变得宽广，对于逆压梯度流动、激波等复杂流动的计算模拟能力相对标准的k-ω模型有较大的提高。

1.3 数值仿真方法验证

采用与前述S弯构型相似的构型(图4)进行数值仿真与试验结果的对比验证。采用结构化网格划分，网格量约为145万。

图4 验证模型计算网格(半模型)

采用前述的数值仿真方法，得到Ma=0.7，α=1°，β=0°时设计点附近进气道对称面上帽罩侧和压缩面上的沿程静压分布曲线，如图5所示。由图可见，计算获得的静压分布曲线和实验相当吻合，说明所采用的数值仿真方法是可靠的。

图5 唇罩与压缩面上压力系数实验值与仿真对比

2 S弯进气道气动特性数值仿真分析

对上述内外流一体化构型进行数值仿真，来流条件为Ma=0.8，飞行高度为13km，当进气道出口马赫数为0.5时，得到的流场马赫数分布等值图如图6所示。可以看出，进入内通道后，相比于入口参数，马赫数有所增加，这是由于S弯通道初始部分面积收缩导致的。同时，在气流向下偏转的过程中，底角落部分开始形成漩涡流动，这是由于此位置侧向的快速扩张，导致的横向压力梯度所致。漩涡所处的范围随着流动向下不断发展，至最低中间截面最为明显，且漩涡内流动速度达到最低，随着向下游的继续发展，漩涡逐渐与主流掺混，其范围有所增加，但与主流的掺混使其速度逐渐接近主流。在流动达到最低截面后，由于通道向上突然的扩张，使上壁面流动发生明显的分离，分离范围随着流动发展变大，且在分离区域内形成流向涡结构。由于通道横向的收缩和纵向的扩张，分离区的范围在横向上不断被挤压，并最终与主流之间形成明显的剪切层。

由于横向压力梯度的影响，整个通道内存在S弯流动中典型的二次流动，并最终影响到出口流动状态，在出口截面形成明显的对涡结构。涡心位置位于通道上半部分，与分离区中心位置接近。

图6 S弯进气道不同截面马赫数分布云图

为了更好地研究其性能，对其质量流量和出口总压恢复系数、出口|DC60|值进行提取。在来流马赫数为0.8、出口截面质量平均马赫数为0.5的情况下，该进气道流量系数约为1.066 3，总压恢复系数0.955，出口|DC60|值为0.418 6。其中，流量系数的计算中所采用的捕获面积使用S弯入口截面面积。

3 几何参数对S弯进气道气动特性的影响研究

3.1 偏移距离对S弯进气道的气动特性影响

为了研究偏移距离对S弯进气道气动性能的影响，分别设计了另外两个偏移距离增加和偏移距离减小的方案。偏移距离定义为最低截面中心位置与入口截面下壁面位置的高度差值。原始构型的偏移距离为0.45L/D，其中L为S弯通道沿x方向的长度；D为出口直径。为了对比，设计了偏移距离为0.4L/D、0.5L/D两个偏移距离增加和减小的方案，面积变化规律等均不改变。采用相同的数值仿真方法和相同的来流条件，出口马赫数仍然匹配为0.5。

图7和图8给出了两个方案的内通道马赫数等值分布图及中间截面和出口截面的马赫数等值分布。偏移距离的增加或者减小基本不改变S弯进气道的流场特征，漩涡的形成与发展、分离区的形成与发展与前述方案基本一致。出口均形成明显的漩涡结构。

图7 偏距减小方案不同截面马赫数分布云图

图8 偏距增加方案不同截面马赫数分布云图

为了进一步对比偏移距离的影响，提取不同构型下的质量流量。出口总压恢复系数及|DC60|值，如表1所示。

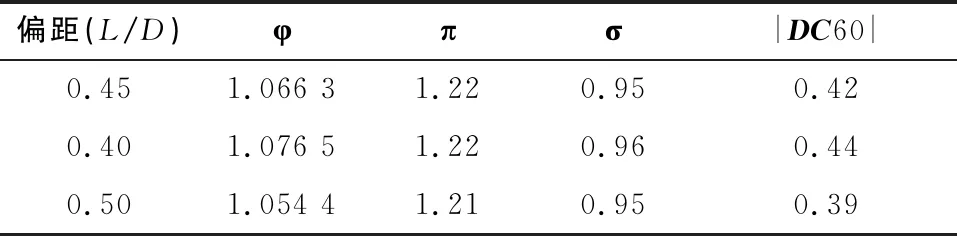
表1 不同偏移距离的进气道出口参数

从表1可以看出在相同的出口马赫数下，进气道质量流量有所差异，随着偏移距离的增加而减小。偏移距离最小的方案总压恢复系数最高，说明过大的偏移距离会增加流动损失，但是随着偏移距离的增加，|DC60|逐渐降低，说明偏移距离的增加有助于通道内流动的掺混，降低出口流场总压畸变。

3.2 长度对S弯进气道的气动特性影响

为了对比S弯内通道长度对S弯进气道气动性能的影响，又设计了两个长度分别加长至3.0m和3.5m的方案，原始构型为2.0m。采用相同的数值仿真方法，出口匹配马赫数仍然为0.5。

图9和图10给出了两个长度改变后方案的内流场马赫数分布及部分特征截面的马赫数分布。随着S弯进气道长度的增加，分离区相对减小，横向涡结构范围也在减小，相应地，出口对涡结构也明显减小范围，这是由于长度逐渐增加后，其余参数没有发生改变，其截面横向的压力梯度有所减弱。

图9 长度3.0 m方案不同截面马赫数分布云图

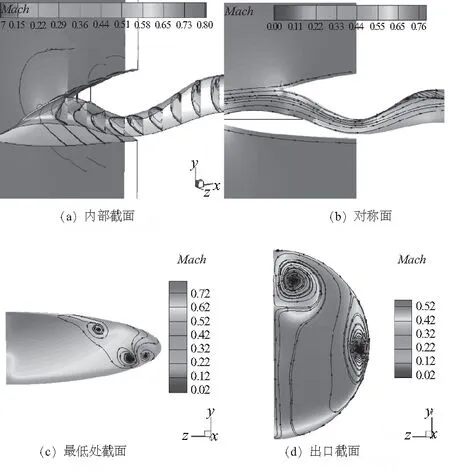
图10 长度3.5 m方案不同截面马赫数分布云图

为了进一步对比长度带来的影响，提取不同进气道的质量流量、出口截面总压恢复系数和出口截面的|DC60|，如表2所示。长度增加后的进气道流量增加，这可能是由于分离区范围的相对减小，使得实际流量面积和损失减小的缘故，总压恢复系数随长度的增加也印证了这一点。随着长度的不断增加，出口|DC60|值不断降低，说明长度的适度增加能够降低出口总压畸变。

表2 不同偏移距离的进气道出口参数

4 结语

本文对某S弯进气道内外流一体化构型进行了研究，并对S弯进气道的偏移距离、长度等参数的影响进行了研究，根据结果可以得到如下结论：

1) 此S弯进气道在入口向下偏转过程中角落形成涡结构，在最低点后向上偏转过程中发生流动分离，横向压力梯度带来了进气道内明显的二次流动，出口形成明显的对涡结构。

2) 进气道偏移距离的增加不改变基本的流场结构，但是会增加流动损失，但适当的增加偏移距离有利于控制出口总压畸变。

3) 进气道长度对性能有明显影响，长度的增加使得二次流动减弱，分离区域减小，同时出口对涡结构范围减小。长度的增加一定程度上会降低总压损失，提升总压恢复系数，同时对控制出口总压畸变有明显好处。