基于切触点高斯过程的直纹面侧铣可靠度分析

李霄

(西安航空职业技术学院，陕西 西安 710089)

0 引言

直纹面是在航空发动机叶轮等关键部件中应用广泛的曲面类型，因其型面复杂且性能易受加工精度影响，且往往存在不确定因素，导致其加工精度可靠性预测困难[1]。为此，分析影响侧铣加工的不确定性因素，建立反映侧铣可靠度的分析模型，对侧铣加工精度的有效分析和准确预测至关重要[2]。

近年来，国内外学者展开了侧铣建模研究。刘佳佳等[3]根据磨床的综合误差传递构建其侧铣加工的近似精度分析模型；WANG Zequn等[4]在综合分析机床误差基础上，建立了某型五轴机床的外圆铣削精度分析模型。目前，蒙特卡洛法等常用侧铣精度可靠分析方法对极限状态函数的依赖较大，不适合求解带有随机时变不确定性变量模型的精度分析问题[5-6]。为此，在超越论[7]及极值法[8]等理论研究和发展基础上，张栋梁等[9]基于主成分分析和多项式混沌扩展提出时变可靠性分析方法，将时间间隔离散化并与瞬时性能函数关联后，采用主成分分析进行降维，然后采用稀疏多项式混沌扩展对降维分量进行近似表示，最后在时变响应的全局替代模型上应用蒙特卡洛方法；HAWCHAR L等[10]在将随机过程进行离散化预处理基础上分析侧铣加式的时变可靠性。这两种方法将动态不确定性模型求解转化为静态模型求解，有效解决了动态不确定性的影响，但其对复杂模型求解时，运算复杂度高且无法确定求解精度。WANG L等[11]对时变模型采用自适应极值改进的响应面法进行求解，计算结果更为精确，但极值响应在多数情况下难以获得精确分布。

为此，综合考虑直纹面侧铣加工中存在的几何误差、刀具参数及动态不确定性等因素，以高斯过程(Gaussian process，GP)描述刀具切触点的坐标误差，构建加工精度分析模型，并以精度指标迭代更新模型，最后通过蒙特卡洛法抽样获得最终可靠度预测。实验结果验证了算法的预测精度和计算效率。

1 侧铣精度可靠度模型

1.1 直纹面切触点坐标变换GP模型

含噪随机函数f(x)的GP模型可由其均值和协方差表示，即f(x)=GP[m(x),k(x,x′)]，m(x)为均值函数，k(x,x′)为协方差函数，x′与x为不同的测试数据。

图1(a)所示为工程中常用直纹面示意图，其矢量表达式为var(y*)=S(u,v)=(1-v)B0(u)+vB1(u)，其中：B0(u)和B1(u)表示直纹面准线函数；u和v分别表示准线与直母线变量参数。图1(b)为通过法向偏置[9]获得的直纹面加工刀位示意图。

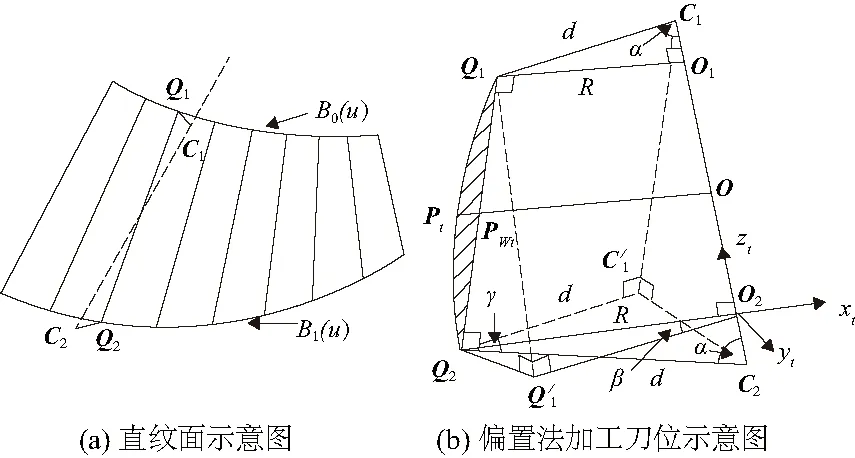
图 1 直纹面及偏置法加工刀位示意图

(1)

式中：d、α值可通过数值迭代[7]计算；O2为刀具端面中心；O1O2为立铣刀的刀位矢量。

x=-Rcos(θ),y=Rsin(θ),z=b·θ/β

(2)

式中0<θ<β。

根据O1和O2坐标，直线Q1Q2方程为：

x=R·(1-cosβ)·z/b,y=R·sinβ·z/b

(3)

联合式(2)和式(3)可以计算Pw和Pt，从而得到切触点的理论误差值，但由于式中R与b存在不确定项，且切触点坐标无法使用显式函数表示，因此Pw、Pt之间距离误差值采用GP高斯随机过程可表示为：

Y(s)=GP[m(s),k(s,s′)]

(4)

以Pts(ptsx,ptsy,ptsz)表示切触点在刀具坐标系三坐标轴方向的GP预测值。

1.2 直纹面侧铣精度可靠度模型

图2所示为某型五轴机床通过位置和姿态特征矩阵构建侧铣加工精度模型，模型忽略工艺温度变化和系统的刚度误差。图中O1为立转台中心，O2、O3和O4分别为主轴、刀具和工件的端面中心，机床、立转台以及摆动转台的原点设置在O1；三轴滑轨与主轴的原点设置在O2；刀具坐标原点设置在O3；工件坐标系的原点设置在O4，各坐标系原点之间的平移矢量分别为P1=PQ2Q1=(x21,y21,z21)T、P2=PQ3Q2=(0,0,z32)T和P3=PQ4Q1=(x41,y41,z41)T。

图2 某型BC 轴五轴机床结构示意图

设切触点坐标的齐次坐标形式为Pt=(ptx,pty,ptz,1)T，其由GP模型预测得到Pts=(ptsx,ptsy,ptsz,1)T，而理想侧铣加工成形点坐标Pw=(pwx,pwy,pwz,1)T。则利用多体特征变换矩阵，将Pts与Pw变换到基坐标系下，即可构建侧铣精度可靠度模型，即

E=T01T12T23Pw-T04T45T56T67T78Pts=(Ex,Ey,Ez,1)

(5)

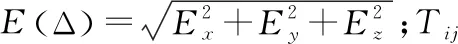
式中：T67=E；Δz87为刀具实测长度方差；x、y、z及B、C为计算刀轴矢量后，通过运动学反变换计算的各轴瞬时参数；ΔβB和ΔγC分别为机床绕y轴和z轴的转动误差；Δxx、Δyy和Δzz为机床沿坐标三轴的平动误差，则模型在允许极限误差情况下的状态函数为：

g[X,Y(s),S]=δ-E(Δ)

(6)

式中：δ为允许极限误差；X为模型的随机不确定量；S为切触点坐标范围。

2 侧铣精度GP模型求解

2.1 随机过程预处理

将切触点坐标范围[0,S]离散为节点s=(s1,…,si,…,sn)，则得到协方差矩阵为：

(7)

式中k(si,sj)表示si与sj两位置的协方差函数。可以看出，协方差矩阵∑是对称正定的，此时，精度模型中Y(s)可以表示为带有随机常数Zi的确定函数的线性组合，即

(8)

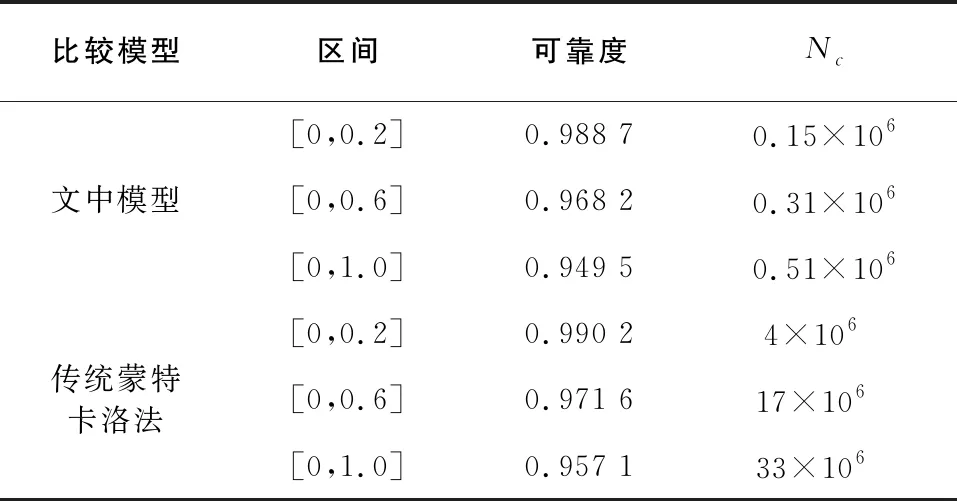
式中：Z=[z1,z2,…,zp]为线性表示中P

(9)

式中：ξ为临界阈值，ξ=0.95。则式(8)可重新表示为g[X,Y(s),S]=g(X,Z,S)，即输入变量转换为两个随机变量[X,Z]，为此，以w=[w1,w2,…]替代[X,Z]作为输入变量，其对数似然函数为：

(10)

式中：I为P维单位矩阵；G为输入的观测值。最大化LGP可以计算模型的超参数，然后在抽样数据下，通过极大似然估计可计算GP模型。对于测试样本w′，GP模型预测值为：

gs(w′,si)=u+rTC-1(G-Au)

(11)

式中：u为预测均值；r描述了w′与训练样本w的相关性，即r(i)=Corr(w′,wi)。

2.2 模型更新与求解

设切触点节点si上某样本点wi被正确预测的概率为Pc(wi,ss)，将模型更新指标设为节点概率期望，当输入m个有效样本时，si上的模型精度指标为：

(12)

(13)

式中I(w)|[0,S]为n个离散节点的模型预测响应函数。通过蒙特卡洛法进行N次抽样后可得切触线精度可靠度值：

(14)

3 算法实验验证分析

为验证文中侧铣可靠度模型的有效性，以LU400 型五轴数控机床为实验对象，采用文献[12]中方法设计曲面，u0=0.02，σ0=0.008，立铣刀直径为6mm。以n=21对u=11.507位置的母线进行节点离散，在机床上加工后通过三坐标测量机检测并获取2万组训练样本，以获得精确的预测数据，对数据进行z-score标准化处理。

3.1 基于实测数据的模型有效性实验

为获得预测坐标值Pts的变化趋势，图3中所示为Y(s)表征的切触点坐标在x轴方向的坐标变化，即ptsx变化。可以看出，在95%的预设置信度范围内，预测数据相对于原始数据具有更小的波动，有利降低部分失效数据的大幅值波动，从而可以确保在后续样本点抽样时的数据稳定。同理，实验测试发现，y轴与z轴的切触点坐标ptsy和ptsz变化在 95%的置信度下，其预测数据的波动幅度更小。因此，3个坐标方向的数据预测响应值表明其更能反映训练数据的变化趋势。

图3 切触点坐标预测ptsx结果

图4 节点s11模型精度指标变化

表1 实验过程模型中间参数

3.2 模型性能比较实验

文中模型通过蒙特卡洛法进行N次抽样后运用指示函数计算切触线精度可靠度值R(0,S)。表2所示为文中采用方法和传统蒙特卡洛法求得的侧铣加工可靠度值，表中节点区间为直纹面某母线的离散节点区间，Nc为两种模型调用状态函数的次数。从表中结果可以看出，文中模型在3种节点范围都取得较高的可靠度，同时，与传统方法相比，其状态函数调用次数减少了一个数量级，从而明显提高了模型的计算效率。

表2 加工精度可靠度对比

图5为参数为1的直母线参数在不同的节点范围下两模型的失效概率变化情况。从图中可以看出，失效概率值随着节点范围的增大，开始时逐渐增大，后逐渐趋于平缓，其变化规律与传统蒙特卡洛方法变化规律一致，说明文中直纹面侧铣模型实现了对节点加工可靠度的有效预测。

图5 位置节点的失效概率值

4 结语

针对不确定因素导致直纹面侧铣精度预测困难及计算效率低的问题，提出了基于刀具切触点GP模型的精度分析方法。首先以高斯随机过程描述引入驱动误差和参数不确定性的刀具切触点坐标误差，然后基于某型机床的误差传递模型，利用多体理论构建直纹面侧铣加工的精度分析模型；通过带有随机常数Zi的确定函数的线性组合方式，简化模型的输入变量，并根据重要性指标和精度指标选择有用样本和更新模型；最后基于蒙特卡洛法获得加工精度可靠度。实验结果表明，所提方法准确预测了加工精度变化趋势，具有较高的计算效率和预测精度，为直纹面侧铣精度预测提供了有效的方法。