以问促思 深度引领

赵霞

问题是思维的起点，创造的开始，学习的开端。没有问题，就没有数学。因此，要追求数学课堂的有效性，教师可以从问题的设计入手。恰当的课堂提问不仅能巩固知识，及时反馈教学信息，而且能激励学生积极参与，激发学生深入思考，启迪学生的智慧。在数学例题教学中，教师尤其要重视问题的设计。下面笔者就以一道例题的教学为例，来谈谈数学例题教学中问题的设计。

例题：如图1，在四边形ABCD中，AC、BD交于点E，△ABE的面积为4，△CDE的面积为16，求四边形ABCD的面积的最小值。

一、提问要能引领“知识溯源”

问题1：本题说到底是一道求面积的问题，初中阶段我们有哪些常用的求面积的方法呢？生1：面积公式法、割补法、比值法。

问题2：这三种求面积的方法一般在什么情况下应用？

师生讨论：面积公式法常用于规则图形的面积求解。割补法一般用于不规则图形的面积计算。我们可以借助割补法将不规则图形转化为规则图形，再算出规则图形的面积，利用规则图形的面积的和或差来求得不规则图形的面积。比值法常用于已知两个图形的面积比的情况，如果有一个图形的面积已知，可以轻松利用这个比值求另一个图形的面积。如果两个三角形相似，我们可以借助相似比求出它们的面积比;如果不相似，我们可以观察这两个三角形是否同高（等高）或同底（等底），如果同高（等高），面积比等于它们的底之比，如果同底（等底），面积比等于它们的高之比，最后再利用这个比值求出另一个三角形的面积。

鉴于数学问题常常运用所学过的知识加以解决，故借助“知识溯源”，可以为处理问题、明确思考方向、发掘解决问题的基本路径找到通，性通法。例題教学中教师通过恰当的提问唤醒学生已有的解题经验，既能巩固学生已有的知识，又能让学生解决问题时有的放矢，有法可依。

二、提问要能引领“学会选择”

问题3：结合条件，你认为用面积公式能求四边形ABCD面积的最小值吗？

生2：整个图形是一个任意的四边形，所以用面积公式法求面积不合适。

问题4：那么用割补法能求四边形ABCD面积的最小值吗？

生3：可以将四边形ABCD的面积看成△ABD和△BCD的面积和，或者四个三角形的面积和，但也解不出来。（教师引导学生交流讨论。学生尝试作出高，如图2，发现此法仍行不通。）

问题5：还有其他割补的方法吗？

当学生发现面积公式法、割补法都不能解决四边形ABCD的面积的最值问题时，就会下意识想到比值法。

在“知识溯源"的基础，上，提问要善于引导.学生对知识方法进行比较，引导学生从条件和结论展开联想，择优选择解题方法，为解题明确方向。这样的提问可以培养学生从众多知识中筛选有用知识的能力，培养学生寻找最优方法的数学思想，提高学生分析、解决问题的能力。

三、提问要能揭示“思想方法”

问题6：现在只剩下用比值法来求面积了，那么用比值法求面积的关键是什么呢？

生4：关键是求出未知图形面积和已知图形面积的比值。

问题7：很好，如图2，那么这里应该求出哪.些图形之间的面积比呢？

生5：应该求出△ADE与△ABE、△CDE与△CBE的面积比，因为这里OABE与△CDE的面积是已知的，如果未知三角形的面积与它们的比值求出来了，就能较容易地求出未知三角形的面积，加之这里△ADE与△ABE、OCDE与△CBE正好等高，它们的面积比就等于DE与BE的比。

问题8：但这里DE与BE的比确定吗？四边形ABCD的面积会随着它们比值的变化而变化吗？

生6：这里DE与BE的比值不确定，它们的比值改变，四边形ABCD的面积也会随之改变。

问题9：四边形ABCD的面积和DE与BE的比值都是变化的量，在数学上有没有可以研究两个变化的量之间关系的数学模型呢？

生7：函数模型可以研究两个变量之间的关系。问题10：那这里的自变量是谁？因变量又是谁？生8：自变量是DE与BE的比值，因变量是四边形ABCD的面积。

问题11：你们会用函数思想来解决这个问题吗？

数学的思想方法是数学的灵魂。例题教学中如何渗透数学的思想方法是教师必须思考的问题。利用阶梯式的提问让学生逐步发现解决问题的思想方法，逐步学会用数学的思想方法看待问题，对于学生养成用数学的眼光看世界是非常有益的。

四、提问要能唤醒“基本数学活动经验

问题12：通过直接设DE与BE的比值，表示出了四边形ABCD的面积的函数表达式。但这个函数表达式好像不是我们学过的类型，那如何来求面积的最小值呢？

生10：我们可以画出这个函数的图像，通过图像来观察它的最小值。

问题13：对于一个陌生函数，我们如何画出它的函数图像呢？大家可参考我们初次接触一次函数时是如何画出它的函数图像的。

生11：我们通过确定一次函数的取值范围，然后列表取很多数值，得到许多对应的点的坐标，然后描点，再用平滑的曲线将点连接起来，发现一次函数的图像是一条直线。

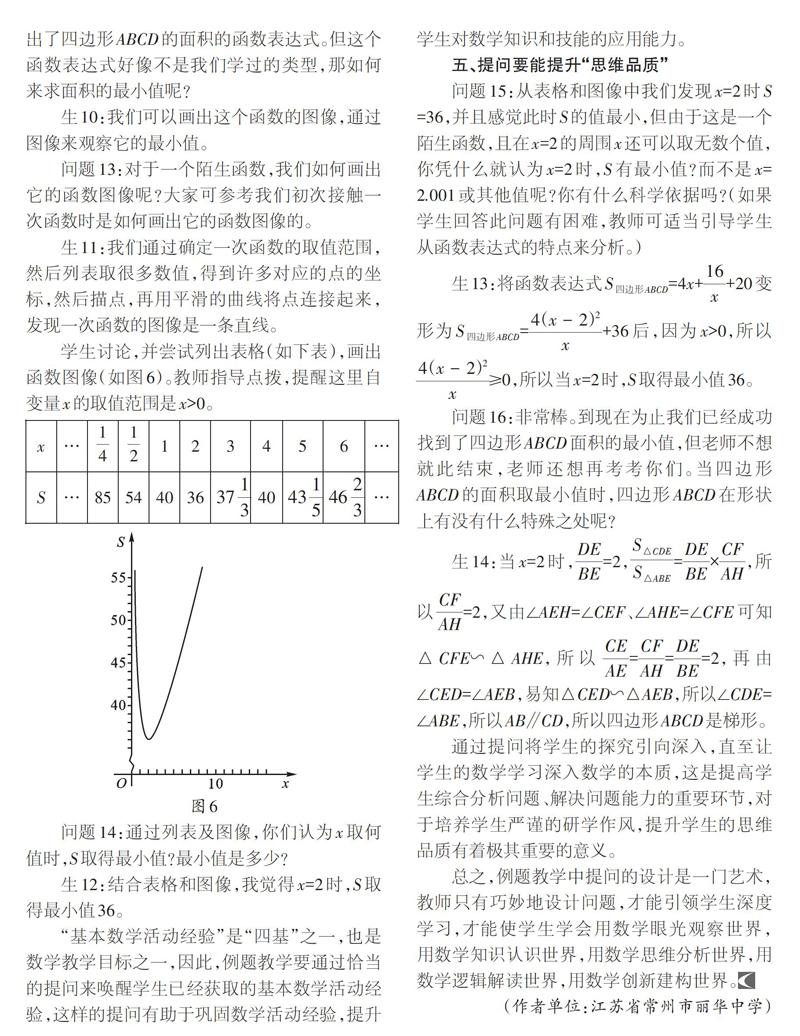
学生讨论，并尝试列出表格（如下表），画出函数图像（如图6）。教师指导点拨，提醒这里自变量x的取值范围是x》0。

问题14：通过列表及图像，你们认为x取何值时，S取得最小值？最小值是多少？

生12：结合表格和图像，我觉得x=2时，S取得最小值36。

“基本数学活动经验”是“四基”之一，也是数学教学目标之一，因此，例题教学要通过恰当的提问来唤醒学生已经获取的基本数学活动经验，这样的提问有助于巩固数学活动经验，提升学生对数学知识和技能的应用能力。

五、提问要能提升“思维品质”

问题15：从表格和图像中我们发现x=2时S=36，并且感觉此时S的值最小，但由于这是一个陌生函数，且在x=2的周围x还可以取无数个值，你凭什么就认为x=2时，S有最小值？而不是x=2.001或其他值呢？你有什么科学依据吗？（如果学生回答此问题有困难，教师可适当引导学生从函数表达式的特点来分析。）

问题16：非常棒。到现在为止我们已经成功找到了四边形ABCD面积的最小值，但老师不想就此结束，老师还想再考考你们。当四边形ABCD的面积取最小值时，四边形ABCD在形状上有没有什么特殊之处呢？

通过提问将学生的探究引向深入，直至让学生的数学学习深入数学的本质，这是提高学生综合分析问题、解决问题能力的重要环节，对于培养学生严谨的研学作风，提升学生的思维品质有着极其重要的意义。

总之，例题教学中提问的设计是一门艺术，教师只有巧妙地设计问题，才能引领学生深度学习，才能使学生学会用数学眼光观察世界，用数学知识认识世界，用数学思维分析世界，用数学逻辑解读世界，用数学创新建构世界。

（作者单位：江苏省常州市丽华中学）