基于PID 和深度卷积神经网络的辐射源识别方法

曹 阳，王金明，徐程骥，岳振军，狄恩彪

（1.陆军工程大学通信工程学院，南京，210007；2.南京国电南自电网自动化有限公司，南京，211153）

引 言

辐射源个体识别（Specific emitter identification，SEI）是电子对抗的重要组成部分，常常通过提取信号的外部特征实现对发射机的分类，是一种非合作的识别手段。由信息传输过程可知，接收机采集到的信号并不是发射端发出的原始信号，还包含了信道、噪声等影响因素。在使用深度神经网络进行辐射源个体分类时，由于信号采集场景单一且样本数量少，网络容易学习到信道、噪声等特征，导致出现过拟合问题[1-2]。为了解决过拟合问题，研究人员提出将数据集按照一定比例随机划分为训练集、验证集和测试集3 个部分，训练集和测试集的数据分别用于训练和测试，验证集用于观察训练过程、调整训练进度以及超参数。正则化[3]、Dropout[4]和Earlystopping 等强化泛化能力的方法都会引入一定的超参数，需要一定量的验证集实现超参数优化。因此以上方法也无法完全解决过拟合问题。深度网络过拟合问题一直是研究热点和难点，基于小样本的学习算法已成为深度网络推广应用的一个核心瓶颈。

本文研究了采集场景单一情况下的辐射源信号分类识别方法。从理论上分析分类识别过程中，深度神经网络产生过拟合的原因，并探索通过在网络输出与输入间增加反馈回路，消除过拟合、提升网络泛化能力的方法。将该方法应用于超短波电台识别时，实验结果表明，该方法有效抑制了过拟合问题，增强了深度卷积神经网络的鲁棒性，提升了辐射源个体识别率，改善了识别效果。

1 卷积神经网络

卷积神经网络（Convolutional neural networks，CNN）是一类包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一[5-6]，目前已经在很多领域得到广泛的应用，尤其是在图像、语音处理等领域发挥着重要的作用。如图1 所示，卷积神经网络一般包含输入层、卷积层、池化层、全连接层、softmax 层和输出层等，输入数据通过一系列卷积和池化操作，经全连接层转为向量，由softmax 层归一化为概率分布。卷积计算公式为

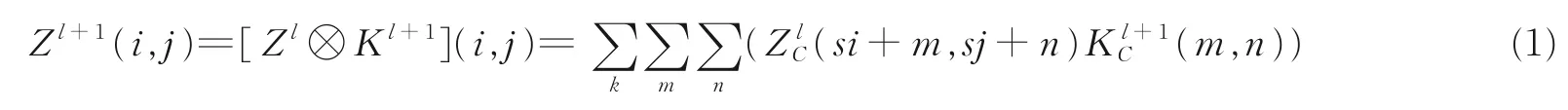
式中：Zl，K，C分别为第l层特征图（Feature map）、卷积核（Convolutional kernel）以及通道（Channel）；m，n，k表示索引；i，j表示像素。

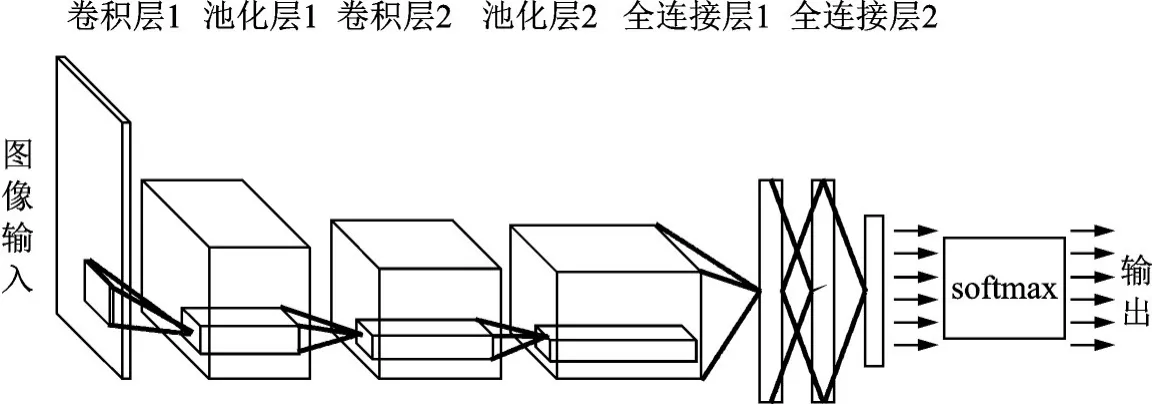
图1 典型的卷积神经网络结构Fig.1 Typical convolutional neural network structure

2 基于PID 和卷积神经网络的辐射源识别方法

2.1 卷积神经网络用于辐射源识别时网络过拟合问题分析

经信道传输后，信号接收机采集得到发射机发射的时域信号，并将其用于辐射源识别。那么接收机采集的信号可表示为

式中：rxi(t)为发射机发出的发射端信号，xi(t)为接收机采集到的信号，Ci(t)、Ni(t)分别为信道特征和背景噪声特征，i为发射机序号。

在卷积神经网络训练过程中，随着迭代次数的增加，训练集的误差会越来越小。而过拟合现象的表现为：训练集误差不断降低的同时，测试集的正确率不仅没有提高，甚至出现下降。

图2 为接收机端信号的特征分布示意图，其中方形区域表示背景噪声特征，3 个圆形区域表示3 部发射机发射端信号特征，椭圆形区域表示信道特征。如果没有信道和噪声的影响，由于信号发射设备硬件上的细微差异，深度神经网络能够学习到每类发射机的信号特征，不同发射机的信号是完全可分的，故图2 中圆形特征区域相互不重叠。但是现实中，传输信道的影响不可忽略，网络还将学习到传输信道的特征。特别是当信号的采集环境较为单一（采集时间段相同、发射机空间位置相近等）时，信道特征会高度相似，进而严重影响深度网络的训练，甚至会导致过拟合。神经网络出现过拟合时，会将具有相似信道特征的输入信号判为一类，从而表现出某一类的数据识别率较高，其他数据识别率相对较低，总体识别率下降。

对于一个三分类的卷积神经网络，当出现上述情况时，3 类电台的分类错误率随迭代次数的变化曲线会出现分层现象，如图3 所示。

对于一个以分类为目标的深度卷积神经网络，毋庸置疑，更高的分类正确率是第一位的。与此同时，网络对每一类的识别能力应当尽可能相近，也就是，希望网络在出现错误分类时，每一类的错误率应服从等概率分布，即

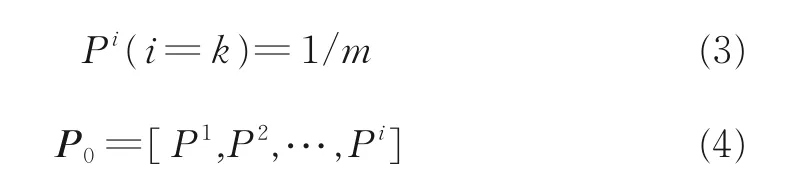
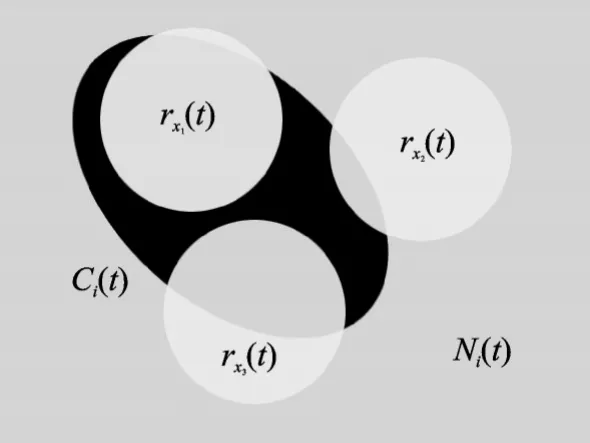
图2 特征分布示意图Fig.2 Feature distribution diagram

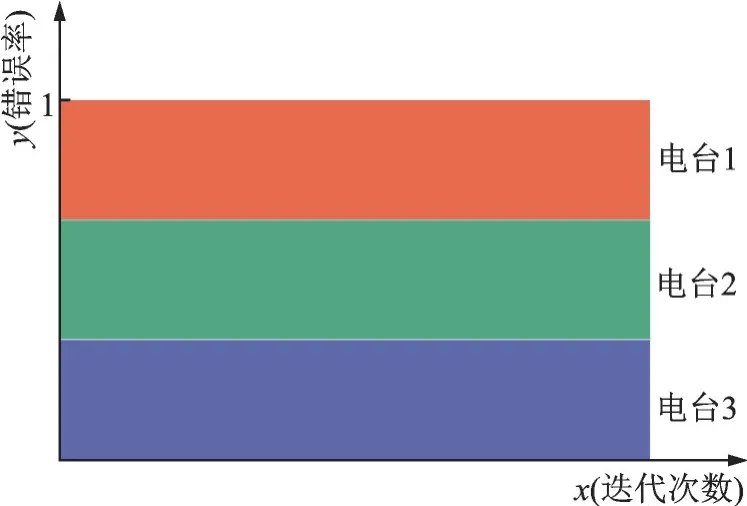
图3 错误率分层现象示意图Fig.3 Diagram of error rate stratification

式中：Pi表示第i类发射机分类错误率,m表示分类数量,P0表示目标分类错误率向量，其服从等概率分布，且维度的值与m相等。

2.2 采用PID 方法解决深度网络过拟合问题

图4 为基于PID 的深度卷积神经网络算法框图，相较于传统的卷积神经网络，在输出与输入间增加一条反馈回路，即图4 中的反馈2 通道。采用PID 算法将输出分类的错误率转化为控制数据分发器的概率，让错误率高的数据以更高的概率参与训练，进行“强化学习”，以达到均衡错误率为目的，进而抑制过拟合。

根据图4 的系统框图，设计了基于PID 的深度卷积神经网络算法，主要从训练过程、PID 算法调控原理和数据分发器3 个方面实现。

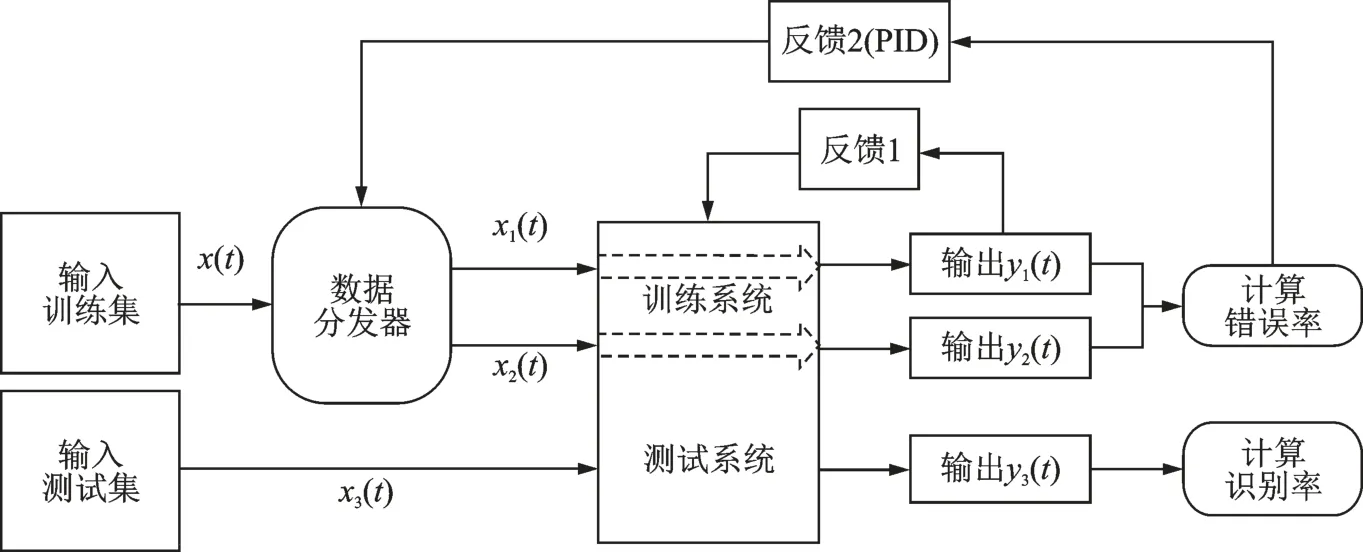
图4 基于PID 的深度卷积神经网络结构图Fig.4 Structure diagram of deep convolutional neural network system based on PID

（1）训练过程。从训练集中取出数据x(t)，通过数据分发器，将数据集分成x1(t)和x2(t)。x1(t)通过训练系统，前向传播后由softmax 层转为概率向量y1(t)，计算损失函数并通过反馈1 通道使用反向传播算法,对网络参数进行调整。同时，x2(t)通过训练系统后，输出为y2(t)，与y1(t)合并计算当前错误率为P(t)。令当前样本标签二值化后为Q(t)，则每个样本的交叉熵损失为

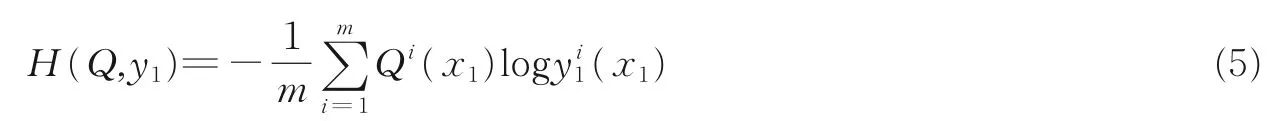
式中m表示分类数量。

（2）PID 算法调控原理。当前错误率为P(t)，目标错误率为P0，则偏差为

控制量为

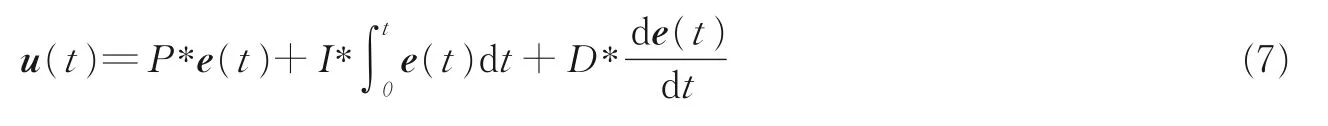
式中P，I，D分别表示比例项、积分项、微分项的系数。

为了便于设计数据分发器，对控制量u(t)进行归一化处理。本文采用常用的sigmoid 函数实现控制量的归一化，该函数表达式为

故而有

（3）数据分发器。数据分发器决定训练集中正常参加训练的数据比例。图5 为本文采用的数据分发器模型，主要由随机数发生器、偏移器、比较器和数据选择器构成。为了保证大部分数据能够参与训练，需要对p(t)增加一个偏移量δ。将偏移后的概率与随机数发生器产生的数据比较，达到控制参加网络训练的数据比例的目的。

为了便于评价网络改进前后的分类效果，系统每迭代训练10 次，计算1 次测试集样本的正确识别率。用N表示待测试样本总数，n表示正确分类的样本数，则正确识别率可表示为

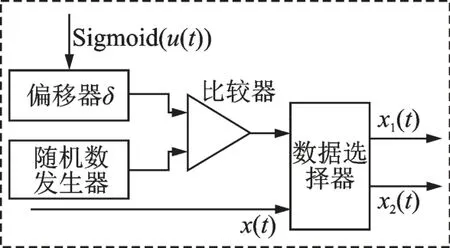
图5 数据分发器构成Fig.5 Data distributor composition

2.3 PID 参数调节

PID 算法由于应用广泛，因而其参数设定的方法也是众多学者的研究方向和重点[7]。使用卷积神经网络实现分类目的，难免需要根据经验调整大量的超参数，本文由于采用了PID 算法，增加了4 个超参数，分别为P，I，D以及偏移量δ。结合前人研究的调参方法，通过多次实验得出了表1 中的数据。

需注意的是，参数设定应该遵循两个原则：（1）逐个调整，灵活搭配。本文先是调整了偏移量，再调整P，最后调整了I。由于网络已取得较好的效果，故D参数未参加调整。PID 参数可根据需要灵活组合使用。（2）参数要适中。参数过大，则表示控制强度过大，调控进入饱和状态，起不到调节作用；参数过小，则调控强度过小，大量数据不能参与训练，导致网络训练不充分，收敛速度变缓。

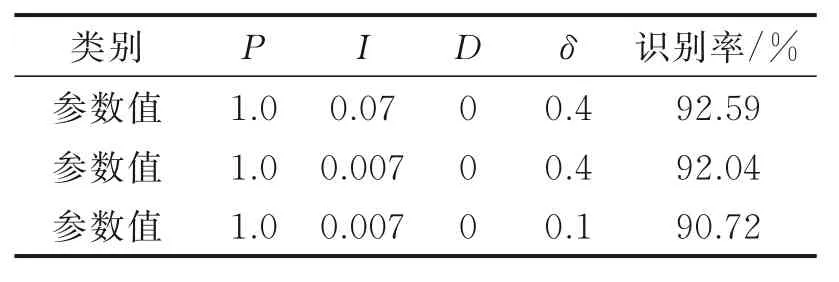
表1 4 种超参数数值Table 1 Four kinds of super parameter values

3 实验仿真

在实验室环境下，采集了3 部超短波电台的辐射信号，每部电台工作在3 个不同的频率（频率间隔2 MHz），工作状态为有导频无语音。电台参数采用双谱特征，双谱是信号高阶谱的一种，由于双谱中包含了丰富的信号细微信息,且受高斯噪声和杂波影响较小，近年来得到了广泛的应用[8]。图6 为一段电台信号提取的三维双谱图。将提取得到的双谱特征按照 9∶1 打乱，随机划分为训练集（1 085 个）和测试集（121 个）。

用来实验的卷积神经网络为10 层网络（含8 个卷积层和2 个全连接层），激活函数为线性整流函数（Rectified linear unit, ReLU），池化方式为最大池化，网络结构如图7 所示。为了防止随着层数的增加导致梯度爆炸或消失，文献[9]基于每一层输出值的方差相等推导出Xavier 参数初始化方式。该初始化方式下的参数服从均匀分布，若ni表示第i层的输入个数，则该分布可表示为

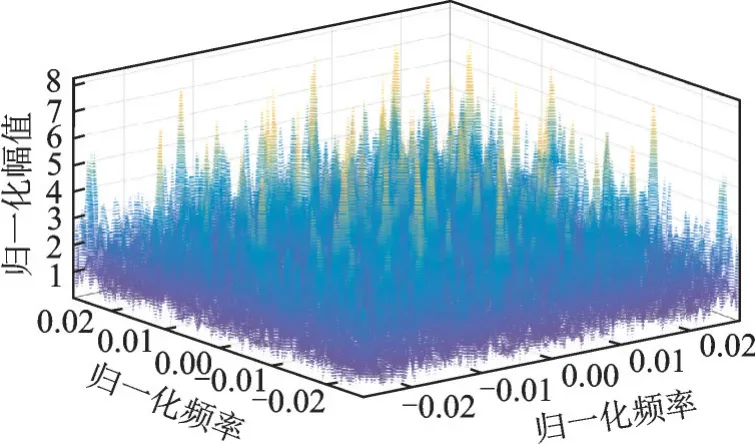
图6 一段电台信号三维双谱图Fig.6 Three-dimensional bispectrum diagram of a radio signal

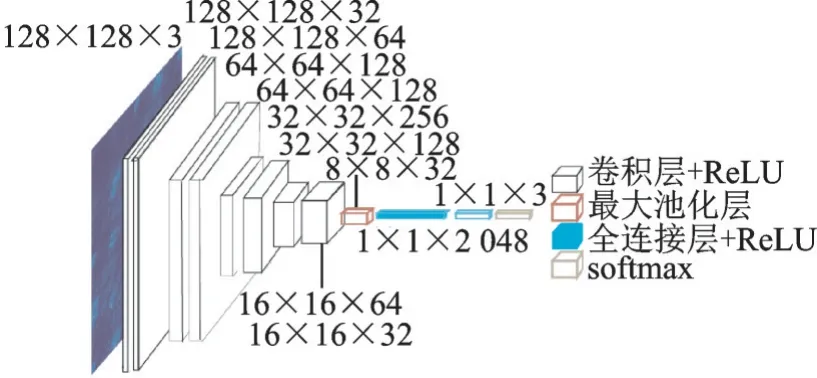
图7 10 层卷积神经网络结构图Fig.7 Ten-layer convolutional neural network structure diagram

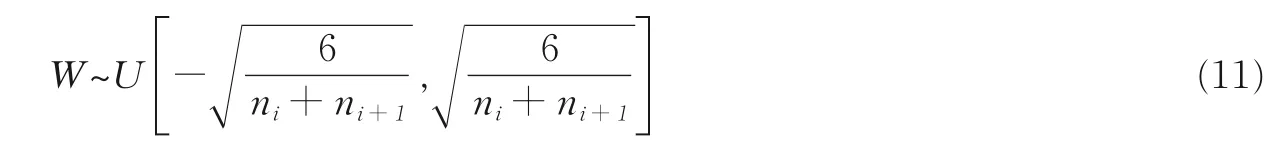
改进前与改进后的网络各训练3 次，实验数据为3 次实验的均值。训练平台为64 位Win10 系统，Python3.6，硬件为小米笔记本Pro，处理器为Intel Core i5-8250U，8 GB 内存。

3.1 过拟合现象及分析

采用传统卷积神经网络进行辐射源个体识别时，识别率随着迭代次数的变化曲线如图8 所示。可以发现：在3 次实验中，识别率都是一开始随着训练迭代次数的增加快速增长，随后趋于稳定，在91%左右，但是最终识别率不仅没有进一步提升，反而出现了识别率曲线纵坐标数值的向下移动。尽管已经使用了Dropout 方法抑制过拟合，但其效果并不理想，识别效果不佳。

3.2 错误率曲线分层现象

传统卷积神经网络训练过程中，识别错误率随着迭代次数的变化曲线如图9 所示。从图9 中可以看出第1 部电台识别错误率较高，而第3 部电台识别错误率较低。由于电台信号是在实验室环境下采集，信噪比较高，噪声带来的影响相对较低。但采集场景的单一，使得电台分类受信道传输影响较大，错误率曲线出现了明显的分层现象。

3.3 改进前后网络分类效果实验

分别得到了传统卷积网络和改进型网络识别错误率的均值和方差，如表2 所示。可以发现通过改进型网络，1 号电台的错误率相对于传统卷积网络的错误率，由0.513 5 降为0.464 7；且3 号电台的错误率由0.119 8 提高到0.196 5，二者都在向着目标概率方向移动。同时，改进型网络的错误率方差明显小于传统卷积神经网络，仅为0.018 0。因此，可以得出结论：本文设计的反馈通道起到了调节作用，含有PID 算法的卷积神经网络能够调整网络的输出分布。

图10 是2 种网络的识别率随迭代次数的变化曲线，传统卷积网络[10]随着迭代次数的增加，识别率在迭代次数为150 左右时，开始出现下降。而改进型卷积网络由于增加了对输出错误率的约束，分类识别率没有因为迭代次数的增加而出现下降。因此可以得出结论：基于PID 算法的卷积神经网络消除了过拟合现象，增强了网络的泛化能力。表3 是两种卷积神经网络的性能参数，从识别率来看，本文算法比传统算法的电台识别率更高，平均识别率为92.59%。从识别率方差来看，本文算法下的识别率方差更小，说明网络识别效果更为稳定。从训练用时来看，本文算法用时更少，较传统卷积网络算法整体用时少了35.3 min，说明算法复杂度较低。

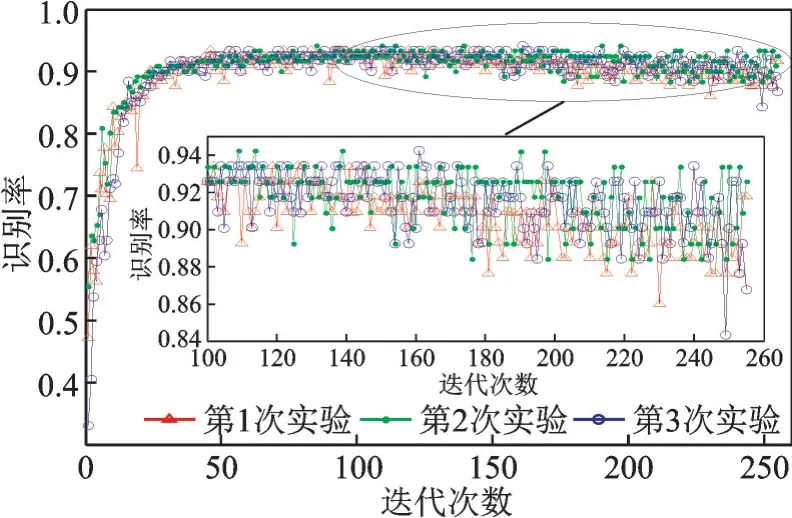
图8 传统卷积神经网络对电台的分类识别效果Fig.8 Classification and recognition effect of traditional convolutional neural networks on radio stations

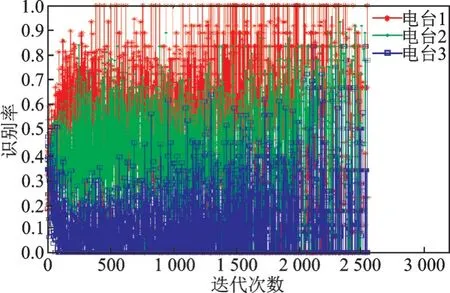
图9 错误率曲线Fig.9 Error rate curve

表2 识别错误率和方差比较Table 2 Identify error rates and variance comparisons

综合来看，基于PID 的卷积神经网络能够更好地完成辐射源个体的分类识别，该算法不仅实现了较高的识别率，还降低了算法复杂度，也提升了算法鲁棒性。

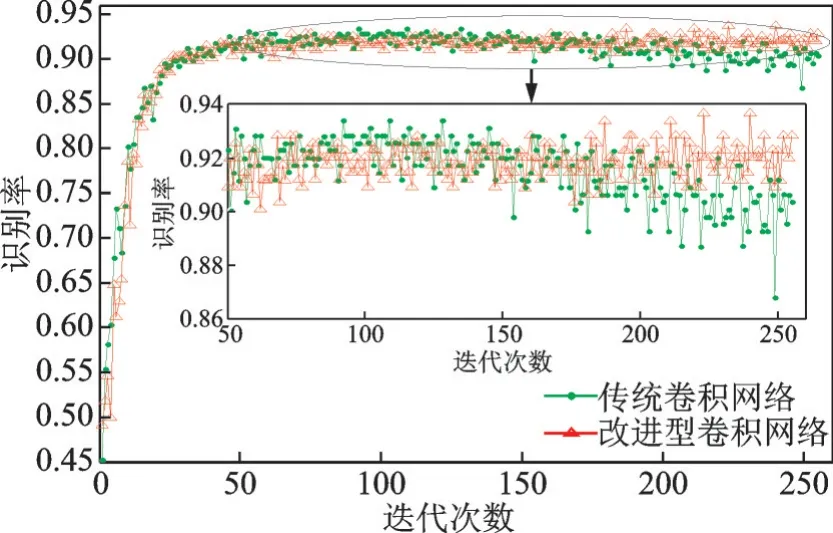
图10 正确识别率曲线Fig.10 Curve of correct recognition rate

表3 两种网络性能比较Table 3 Two kinds of network performance comparison

4 结束语

本文对辐射源识别方法进行了研究，针对辐射源信号样本数据采集场景单一、数量较少，导致卷积神经网络出现过拟合问题，提出了基于PID 和卷积神经网络的辐射源个体识别算法。将该算法用于通信电台的识别，实验结果表明，本文算法比传统算法识别率高，平均识别率为92.59%；识别率方差更小，该算法下的识别率方差约为传统算法的1/3，说明改进型网络识别效果更为稳定；训练用时较少，该算法训练速度比传统网络快，算法复杂度更低。总的来说，基于PID 和深度卷积神经网络的识别算法能够完成辐射源个体的分类识别，该算法在保证了较高的识别率的同时，抑制了过拟合，降低了算法复杂度，提高了深度网络的鲁棒性。同时，本文算法也为自适应调参提供了一种研究思路。