基于截断核范数低秩分解的自适应字典学习算法

杜秀丽 ，司增辉 ，左思铭 ，邱少明

（1.大连大学通信与网络重点实验室，大连，116622；2.大连大学信息工程学院，大连，116622）

引 言

压缩感知（Compressed sensing, CS）是一种寻找欠定线性系统稀疏解的技术。压缩感知相较于Nyquist 采样定律，突破了“先采集再压缩”的限制，将采样和压缩结合起来，该理论被广泛应用于人脸识别、医疗成像、信号处理和遥感成像等领域[1-2]。

压缩感知理论中，图像信号在字典下的稀疏系数越稀疏则图像重构效果越好[3]，所以通过何种方法得到与图像特性相匹配的字典非常重要。当前字典训练方法可以分为两类：解析方法和学习方法。解析方法使用一些数学变换和适量的参数来构造字典，这种方法的优势在于相对简单，计算复杂度低，但缺点也十分明显，由于字典中的原子是根据数学变换得到，所以字典原子形态单一，不能与图像本身的复杂结构形成最佳匹配，即非最优表示。近年来字典学习方法研究有了长足的发展，该方法通过学习图像信号中的信息，来不断地更新字典中的原子，使得原子包含更加丰富的信息，更加贴合图像信号的特性。研究者们提出了许多新的字典学习理论，早期有多成分字典（Multi-component dictionary）[4]、奇异值分解（Singular value decomposition, SVD）字典[5]等，随后Engan 等[6]提出了最优方向法（Method of optimal directions, MOD）。现在使用最多的字典学习方法是Aharon 等[7]提出的K-奇异值分解（K-singular value decomposition, K-SVD）算法，与MOD 算法略有不同，K-SVD 算法不是对整个字典进行更新, 而是对字典原子逐个进行更新，进而训练出与图像相匹配的过完备字典。

在实际应用中图像数据容易受到噪声干扰，直接对图像进行字典训练易受到噪声的影响，导致训练出来的字典对图像的稀疏表示能力下降，图像重构的质量不高。近年来，研究者们在图像去噪方面作了很多研究，其中低秩稀疏分解在去噪方面表现出了良好的效果。Zhou 等[8]使用主成分追踪算法来对含有高斯噪声的低秩矩阵进行分解，剔除图像中的噪声，从而得到数据低秩部分。胡正平等[9]针对阴影、遮挡等破坏图像低秩结构的问题，提出了基于低秩子空间恢复的联合稀疏表示识别算法来恢复出图像的低秩部分，实验结果证明提高了识别率。由于在对矩阵进行低秩分解时，主要通过使用矩阵的核范数来对秩函数进行逼近，2013 年，Hu 等[10]发现已有的核范数方法并不能在真实的应用中得到较好的低秩解，因为在核范数最小化过程中，所有的奇异值需要同时被最小化，不能很好地近似秩函数，因此提出了截断核范数(Truncated nuclear norm regularization, TNNR)作为秩函数的另一种逼近方式，并且在实际应用中取得了良好的效果。Cao 等[11]为了恢复出矩阵的低秩和稀疏分量，讨论了截断核范数在矩阵恢复上的收敛性，并对各种数据集进行了一系列的比较实验，证明了截断核范数正则化低秩分解算法能够去除图像噪声，并且与其他方法相比该方法在恢复矩阵的低秩和稀疏分量方面更加有效和准确。Geng 等[12]将群体稀疏表示视为低秩矩阵逼近问题，采用截断核规范最小化方法可以更好地恢复出低秩矩阵，并从恢复出来低秩部分中学习出字典，并利用实验证明了使用该方法训练得到的字典能够对图像进行有效的稀疏表示以及优良的重构效果。

传统分块压缩感知中，通过分割得到的图像块仅训练一个字典，由于各个图像块所包含的纹理特征并不相同，因此一个字典并不能保证对各个图像块都有优质的稀疏表示[13]。本课题组曾对大数据量的图像数据库，将图像库分割为相同大小的图像块，使用灰度熵作为纹理复杂度的度量对图像块进行分类，再使用不同类别的图像块，训练出多个不同大小的最优稀疏表示字典[14]。

为进一步提高图像重构的质量，在基于图像灰度熵的自适应字典学习算法[14]的基础之上，本文提出基于截断核范数低秩分解的自适应字典学习算法。图像通过矩阵低秩分解可以分解出包含图像原始信息的低秩部分和由高频噪声及物体轮廓信息组成的稀疏部分[15]，同时考虑到现有的基于核范数的优化方法对于低秩分解算法的近似逼近不能得到最优解的问题，使用截断核范数作为低秩分解中秩函数的近似逼近，得到不含噪声的低秩部分，将低秩部分进行分块和分类，对每一类图像子块进行字典训练，进一步对图像块进行准确稀疏表示，减少图像数据的传输量。图像重构时只对低秩部分进行重构，组合稀疏部分恢复原图像，以提高图像重构质量和字典抗噪能力。

1 矩阵低秩稀疏分解理论

1.1 低秩稀疏分解

任意一个矩阵都可以进行低秩分解，利用低秩近似，可从受到噪声污染的图像中恢复出原始图像[16]。在实际应用中，图像数据一般以矩阵形式存储，且所给定的实际问题中的图像矩阵通常具有低秩性，但在图像数据采集过程中通常会受到高频噪声污染，破坏了图像之间的结构性，使得图像质量明显下降。因此，本文选择使用低秩分解算法，将图像分成低秩与稀疏两部分，对图像的低秩部分进行字典学习与稀疏表示，相较于直接对图像进行字典学习的算法，能够剔除图像采集过程中所产生高频噪声的影响[17]，能够更好地重构出原始图像。

现有的低秩分解算法将受到噪声污染的矩阵X分解为低秩矩阵Z与稀疏矩阵E，即X=Z+E，且矩阵Z和矩阵E均是未知的。为了求解低秩矩阵Z，将上述问题转化为求解一个目标优化问题，即

式中：rank(⋅)为秩函数，λ为正则化项参数，l0范数表示矩阵中非零的元素个数，使得矩阵E具有稀疏性。因为秩函数非凸且不连续，所以对式(1)中目标函数的求解是NP 难问题。Recht 等[18]发现在压缩感知中，如果对于定义约束的线性变换具有一定的受限制等距特性，则可以通过解决凸优化问题来恢复最小秩解，使得通过矩阵核范数来近似逼近秩函数恢复出图像的低秩部分成为可能，由于l1范数表示矩阵中元素绝对值之和，相较于l0范数有更好的求解特性，从而可将式(1)中目标函数转化为凸优化问题，即

1.2 截断核范数

截断核范数只对数值较小部分敏感，所以只要目标矩阵存在低秩结构，就可以通过对最小化核范数问题的求解得到最优的低秩解，能很好地对秩函数近似逼近。使用截断核范数的方法作为秩函数的另一种近似逼近方法，能够对矩阵结构获得比传统核范数更好的近似估计，并且在实际应用中取得了较好的近似表示效果[19]。截断核范数定义为：对任意的矩阵X∈Rm×n，将其奇异值按降序排列，把截断核范数记为表示后 min(m,n)-r个奇异值的和，即

式中δi(X)表示X的第i个奇异值。

由该定义可以看出，与传统的核范数方法不同的是，截断核范数并不最小化所有奇异值的和，仅最小化较小的min(m,n)-r个奇异值。只要低秩解存在，求解截断核范数便可以得到低秩解，且这种方法获得的对秩函数的近似解更具鲁棒性，更精确。因此，通过定义可知截断核范数具有如下性质[20]：对于 任 意 矩 阵X∈Rm×n，任 意 矩 阵A∈Rr×m，B∈Rr×n，且 有AAT=I，BBT=I。 对 于 任 意 不 大 于min(m,n)的非负整数r，可以得到

1.3 截断核范数正则化低秩稀疏分解模型

根据前文描述，本文使用基于截断核范数正则化的低秩稀疏分解(Low rank and sparse decomposition with truncated nuclear norm regularization, LRSD-TNN)模型可表示为

因为截断核范数通常是非凸的，常用的凸优化算法不能对该问题进行求解，但是，结合截断核范数的定义和数学理论中奇异值分解理论知识，可将非凸优化问题转化为凸优化问题。

矩阵X奇异值分解可表示为

式中：U=[u1,u2,…,um]∈ Rm×m，Σ∈ Rm×n，V=[v1,v2,…,vn]∈ Rn×n。令

根据酉矩阵的性质，有AAT=Ir×r且BBT=I r×r，从而可得

由式(4,8)，可得

因此

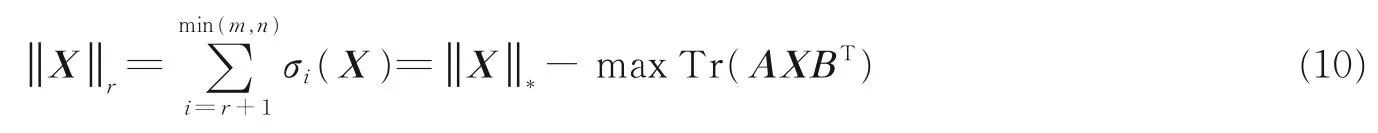
由式(10)和式(5)中模型，可等价求解

式中：A∈ Rr×m，B∈ Rr×n。

如何更加有效地求解式(11)的凸优化问题极其关键。本文使用交替方向乘子(Alternative direct method of the multiple, ADMM)算法[21]对该问题进行求解。ADMM 是一种用来求解线性等式约束凸优化问题的有效算法，其算法思想可应用在求解非凸优化问题上，且其收敛性已经得到验证[22]。

2 基于截断核函数低秩分解的自适应字典学习算法

2.1 K-奇异值分解算法

K-SVD 算法是一种非常经典的字典训练算法，解决了高维矩阵求解的问题，达到了较好的字典训练效果。该算法思想通过最小化误差来不断的迭代得到最优解。首先初始化字典，利用奇异值分解算法通过该字典计算出对应的表示系数，然后根据固定下来的表示系数依次更新字典中的每一个原子，在字典和表示系数之间不断迭代，直到满足最小误差时停止。

对图像信号X∈Rn通过字典进行稀疏表示，即

式中：D∈ Rn×T为过完备字典含有T个原子，dj为字典原子，为列向量，θ∈ RT为X在字典D上的稀疏表示系数。然而，在使用字典对图像信号X进行稀疏表示时都会存在一定的误差，即

把N个信号整合到一起记为稀疏系数矩阵设为Θ，其中一种迭代终止条件是稀疏系数在给定l0范数条件下求解出最优稀疏逼近解，求解如式(14)所示。

式中：ξ为每个稀疏系数在l0范数下的最大值。另一种终止条件是逼近误差在满足条件下求解最优稀疏系数，求解如式(15)所示。

式中：ε为稀疏逼近误差的最大值。同时考虑稀疏系数的稀疏性和逼近误差两个条件，求解如式(16)所示。

由于K-SVD 算法中对字典原子的更新是逐列进行的，为了更好地描述字典原子与系数系数之间的更新方式，将字典和稀疏矩阵进一步展开，字典D中第k列dk对应系数矩阵Θ中第k行的，则求解如式(17)所示。

从式（17）可以看出，把DΘ分解为k个且秩为1 的矩阵，可以假定其他k-1 项是固定的，剩下的第k项待更新。矩阵Ek可以看成去除原子dk后，在N个图像信号样本中产生的逼近误差。先对系数中的非零值进行保留来确保的稀疏性，再对Ek使用SVD 分解算法来更新dk和。

2.2 基于截断核函数低秩分解的自适应字典学习

由于矩阵低秩分解算法能够提取出保留图像初始信息的低秩部分和具有高频噪声及物体轮廓信息的稀疏部分，通过对包含有图像原始信息的低秩部分进行分类字典训练，能够更好地体现出图像不同块的纹理信息，提高字典的适应性，进而提高压缩感知后的图像重构质量。因此，本文提出了基于截断核范数低秩分解的自适应字典学习算法（Adaptive dictionary learning algorithm based on low rank and sparse decomposition with truncated nuclear norm, ADLA-LRSD-TNN），算法流程框图如图1 所示。本文所提算法使用大数据量的图像库作为训练样本，首先使用基于截断核范数的矩阵低秩分解算法对图像库训练集中的图像进行低秩分解，取得训练集图像库的低秩部分，然后对低秩部分进行分块，根据图像纹理复杂度对图像块进行分类，对于不同类的图像块，初始化对应不同大小的字典，通过K-SVD 算法训练更新字典，最终得到训练好的多个字典，对于待感知图像使用训练好的字典进行稀疏表示。随着图像库的不断增加，新图像的稀疏表示性能就越好。

本文算法的整体步骤如下：

步骤1将图像库中训练集的所有图像使用基于截断核范数的低秩分解算法分解为低秩部分和稀疏部分，然后将训练集的低秩部分进行图像块分割，分为S个B×B大小的图像块，将S个图像块矩阵变换为列向量，将S个列向量排列成一个B2×S大小的训练集数据矩阵M2。

步骤2计算矩阵M2每一列的纹理复杂度，依据纹理复杂度升序的方式重新对M2中的所有列进行排序，排序后矩阵变为M2v。将纹理复杂度的最小值和最大值之间的区间分成C等分，得到C个分类后的图像块集合M2c(i)(i=1,2,…,C)。

图1 基于截断核范数低秩分解自适应字典学习算法的整体框架图Fig.1 The overall framework of adaptive dictionary learning algorithm based on truncated nuclear norm low rank decomposition

步骤3对每类图像块数据M2c(i)使用K-SVD 算法训练过完备字典，根据当前类图像块的纹理复杂度训练出原子个数不同的多个字典。对纹理复杂度低的图像类，其包含的图像特征信息较少，含有较少原子数的字典就能对其进行最优的稀疏表示。对纹理复杂度较高的图像类时，其包含的图像细节较多，因此需要使用原子数目更多的字典才可以对其进行最优的稀疏表示，从而训练出较大的过完备字典。最后保存好训练得到的多个字典用来对新图像进行稀疏表示。

步骤4对新图像，同样先对图像进行低秩分解，得到图像的低秩部分，然后将低秩部分同样分解为B×B大小的子块，将每个图像子块矩阵变为列向量形式。计算每一列的纹理复杂度，然后按从小到大的方式排列，按照图像库训练集低秩部分纹理复杂度均值，同样分为C类。将新图像低秩部分的各个类使用相应类训练得到的冗余字典对其进行重构。

3 实验对比与仿真分析

为了验证本文提出算法的性能，使用灰度熵作为纹理复杂度的衡量标准对图像库中的图像子块进行分类，利用基于截断核范数矩阵低秩分解算法提取图像低秩部分，然后进行分类字典学习（ADLA-LRSD-TNN），并与不使用截断核范数低秩分解直接对灰度熵直方图分类后的图像子块进行分类字典学习（ADLA-IGE）的结果[14]，以方差作为纹理复杂度的衡量标准进行分类字典学习[23]和不分类的K-SVD 字典学习这3 种算法进行对比。

实验所使用的数据来自于加利福尼亚理工学院收集的101 类图像数据库（Caltech101），每一类大约40～800 幅图像，共有 9 146 个图像。

为保证实验验证有效，从飞机类图像库中选择前400 幅图像作为训练集，其余图像作为测试集，分别使用4 种算法分别对训练集进行字典训练，得到多个不同大小的过完备字典。并随机从训练集和测试集中各取出100 幅图像，使用上述4 种算法训练得到的字典对其进行重构，4 种算法均使用相同的重构算法，KSVD 迭代次数均设为20 次，在数据观测时使用采样率为0.5 的观测矩阵对图像进行观测，将重构效果进行对比，重构的PSNR 值结果如表1 与表2 所示。

表1 4 种算法对于训练集的重构PSNR 值对比Table 1 Comparison of PSNR values of the four algorithms for the reconstruction of training sets dB

表2 4 种算法对于测试集的重构PSNR 值对比Table 2 Comparison of PSNR values of the four algorithms for the reconstruction of test sets dB

由表1 和表2 可以看出，在相同分类层数的情况下，对于训练集和测试集4 种算法均能达到较好的重构效果。对于训练集的重构效果要高于对于测试集的重构效果，因为字典是通过训练集训练得到的，能更好地提取出训练集图像的纹理度信息，从而更好地对其进行重构和稀疏表示。

从实验结果可以看出，在先使用基于LRSD-TNN 算法得到图像的低秩与稀疏部分之后，再对图像的低秩部分进行灰度直方图分类得到的重构效果均要高于直接对原始图像进行灰度直方图分类和方差分类以及不分类的K-SVD 的重构效果。并且在对于训练集和测试集进行重构时可以发现，使用两种算法得到的重构结果均在5 类时略微下降而在6 类时又能有所提升。这是由于采样率过低，不能有充足的采样点对图像进行采样，当分类数由4 类变到5 类时，每一类之间的灰度熵差值并不大，而分类数的增加导致每一类中图像数据减少，从而重构质量降低。而当分类数为6 类时，即分类数量足够大时，图像分类的更加精确，各类图像块之间的灰度熵差距够明显，训练多个字典能够更好地反映不同图像块的纹理复杂度，重构质量又能有所提升，并将随着分类数的增加而提高。

为了使仿真结果更为直观可见，使用飞机图像、人物图像、房屋图像、帆船图像和磁共振图像在采样率为0.5 的观测矩阵进行观测，进行6 类字典重构，计算出每幅图像的PSNR 值，并记录在每幅图像的下方，实验结果如图2 所示。其中第1 列为原图，第2 列为ADLA-LRSD-TNN 算法重构图，第3 列为ADLA-IGE 算法重构图，第4 列为方差算法重构图，第5 列为K-SVD 算法重构图。

纵观图2 可以明显看出，使用ADLA-LRSD-TNN 算法进行字典学习重构后图像的PSNR 值都优于其他3 种算法，图像的重构质量同样优于其他3 种算法，这是因为通过LRSD-TNN 算法恢复出的低秩部分剔除了噪声的影响，从而训练出的字典排除了噪声的影响，使得重构质量进一步提高。横观图2可以看出，其中房屋图像和磁共振图像4 种算法的重构质量都高于其他3 种图像，通过原图像可以看出，房屋图像和磁共振图像的图像纹理相对简单，这才使得重构后的图像有较好的PSNR。因此本文所提算法训练得到的字典对于图像的重构质量要高于其他3 种算法。

图2 不同图像使用4 种算法算法在采样率为0.5 下的重构图像和PSNRFig.2 Reconstruct images and PSNR of four algorithms at a sampling rate of 0.5 for different images

仿真实验结果表明，对基于截断核范数的低秩分解算法得到的图像矩阵低秩部分使用灰度熵直方图分类算法能更好地体现图像的纹理度，能够得到更好的过完备字典，能对图像信号进行更好的稀疏表示与重构，重构质量相较于直接对原始图像进行灰度熵分类和字典训练能够有所明显的提升。

4 结束语

针对图像压缩感知字典学习算法，没有考虑到图像容易受到高频稀疏噪声的影响、不同图像块包含的图像信息不同、仅训练一个固定字典的问题，提出了基于灰度熵直方图的截断核函数低秩分解自适应字典学习算法。本文利用基于截断核范数的低秩分解算法将大规模图像库分为低秩与稀疏两部分，并依据灰度熵作为纹理复杂度衡量标准来对图像块进行分类，将图像库的低秩部分分为多个类别，对不同类别的低秩图像块，初始化包含不同原子个数的字典，通过K-SVD 算法训练得到多个过完备字典，对于待感知图像使用图像库的灰度熵直方图类别进行分类，并使用图像库相应类别训练得到的过完备字典对各个类进行稀疏表示。仿真结果表明，本文所提算法能够对图像进行较好的稀疏表示，并在很好的保持图像块特征一致性的同时显著提升图像重构质量。