基于模糊C均值聚类推理模型的高铁土建工程造价智能估算
高立扬, 牛衍亮, 张小平
(1.中铁二十局集团有限公司 第四工程有限公司,山东 青岛 266061;2.石家庄铁道大学 经济管理学院,河北 石家庄 050043;3.河北地质大学,河北 石家庄 050031)
一、引言
高速铁路建设项目规模大、投资额大、结构复杂、技术要求高,同时也受到时间、地域、市场价格、施工设计方案等复杂因素的影响,这对于有效控制造价提出更高的要求。我国传统的项目投资估算方法大部分是直接按照定额确定的子目价格来计算,定额指标是根据地区的整体发展情况而编制,一般而言动态性低。也有一些使用单位生产能力估算法、生产能力指数估算法、比例估算法、朗格系数法、资金周转率法等方法,这些计算方法大都建立了造价与指标的简单线性关系模型,未考虑到这是一个复杂的网络结构。因此,在社会智能化发展的背景下,文章立足于可行性研究决策阶段,从非线性造价预测的角度,对高铁土建工程的造价进行估算。
Zadeh[1]提出了模糊集合的概念,随后又将模糊集引入到推理领域,由此开创了模糊推理技术。模糊推理基于模糊理论被越来越多地应用到构建非线性模型来解决实际问题。周涛等[2]研究了数据挖掘中模糊聚类方法并提出了新的发展方向。程敏等[3]在结合利用专家经验建立的模糊规则作为影响风险的主要变化情况下,基于传统的FMEA方法建立模糊推理系统。冯翰等[4]立足于电力项目的造价估算,将模糊C均值聚类同PSO-SVM相结合,建立非线性模糊推理模型。段晓晨等[5]在查询已完数据库后发现与拟建项目没有类似项目,通过专家经验确定的项目造价因子作为模型的输入变量,融合影响造价变化的模糊规则得出拟建项目的造价。王攀等[6]针对硬岩掘进机(TBM)在复杂地质条件下的可掘进性,进行了系统及定量的研究,基于模糊聚类理论和施工样本数据分析,建立了可掘进性分级预测模型。杨茂等[7]对多步滚动预测模式进行了分析,并建立ANFIS(自适应神经模糊推理系统)预测模型。罗频捷等[8]采用基于遗传算法的模糊神经网络模型对公交到站时间进行预测。余飞鸿等[9]通过改进的模糊C均值聚类(IFCM)算法将光伏出力历史数据和待预测日数据聚类,利用遗传膜优化BP神经网络预测模型(GAPS-BP)进行预测。
综上,文章首先基于显著性成本理论确定影响高铁土建工程造价的显著性成本因子。然后运用模糊C均值聚类将已完工程聚类,得出不同类别的已完工程的造价区间;同时,当拟建工程已知的工程特征不足识别的显著性成本因子的数量时,运用模糊C均值聚类算法将显著性成本因子聚类,得出新的拟建项目的显著性成本因子。最后,构建模糊推理非线性造价智能估算模型,对高铁土建工程进行投资估算。
二、基于显著性成本理论的显著性成本因子识别及量化
在国外大量的研究中发现,在清单的分项工程中,有占18%的显著性成本项目的成本占项目总成本的81%,也就是约为20%的项目大概占据总造价的80%。这被称为显著性成本理论,其源于“二八原则”(其中约为20%的项目成为显著性成本项目)。同时,不同的项目具有类似的显著性成本项目。虽然只研究20%的项目对于总体数量比例小,但是这对于减少计算误差却有显著意义,可以有效降低造价误差。
根据平均值法可以选取影响搜集到的40个已完工程造价的显著性成本因子,这40个已完工程作为文章研究的数据库。即
式中,C为高铁项目土建工程总造价;N为高铁项目土建工程的工程特征个数;T为高铁项目土建工程特征平均造价。根据平均法得出,在清单中的139个分项工程中,有34个工程特征(占全部工程特征的20%左右)的造价均比平均造价高,并且对各个已完工程的34个工程特征的造价求和后,发现其占据整个土建工程造价的80%左右,因此将其确定为影响造价的显著性成本因子,并且不同的高铁项目土建工程都具有类似的显著性成本因子。将这些显著性成本因子进行整理后,得出影响高铁土建工程造价的显著性成本因子如表1所示(文章研究二级指标)。

表1 高铁土建工程造价显著性成本因子
针对不同的评价指标,将指标进行量化处理。可以对任意一个高速铁路项目的显著性成本因子进行定量化描述,若一个显著性成本因子由多种类目组成,则计算其加权平均值作为该工程特征的量化值,同时,指标量化分为定性和定量。根据显著性成本因子对造价的影响程度,得出的显著性成本因子的量化结果如表2所示。由于篇幅要求,只列出部分量化结果,全部已完工程的显著性成本因子及其量化值;如有需要,也可向作者索取。
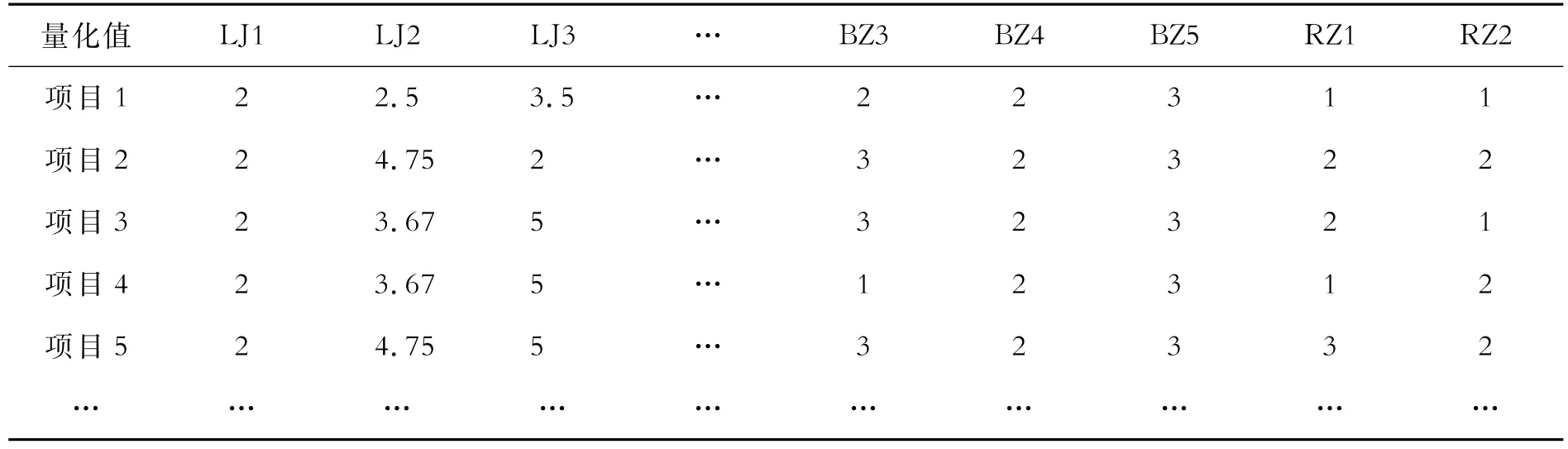
表2 已完工程显著性成本因子量化结果
三、基于模糊C均值聚类推理的高铁土建工程造价智能估算模型构建
(一)模糊C均值聚类
Dunn将硬划分的C均值算法运用到模型的模糊划分当中,在这过程中为了得到较为科学的聚类划分,Dunn确定每个样本与各个聚类中心的距离的方法是运用隶属度的平方加权。

式中,C为达到的聚类的数目(2≤C≤N);uij为第i类中指标x k的隶属度;v i为第i类的聚类中心。
Bezdek又在此基础上,进行推广,得到基于目标函数的模糊聚类更具一般性的描述。

式中,m∈[1,+∞)为加权指数,又称作平滑指数。
模糊C均值聚类算法的计算过程为:
步骤一,初始化。首先确定模型的聚类数目为C,2≤C≤N,N为进行运算的初始数据的个数。
步骤二,计算或重新划分矩阵U。

步骤三,更新聚类中心V。
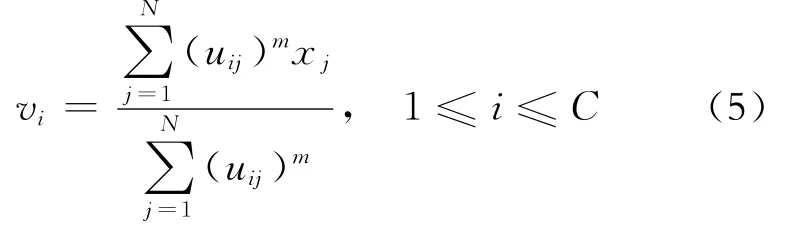
模糊C均值聚类算法有很深的数学理论基础,是软化分在硬划分的基础上,又加以改进的算法,可以更大程度上进行非线性函数的运算。因此对于文章对项目的聚类划分,模糊C均值聚类具有很强的适用性。
运用模糊C均值聚类方法以上运算步骤,借助于MATLAB R2016a将已完工程聚类,可以得到已完工程的造价区间;当拟建工程的已知工程特征数量不足显著性成本因子数量时,则运用模糊C均值聚类方法将显著性成本因子聚类,得到新的因子作为拟建工程单位造价预测的依据,然后将其同模糊规则输入模糊推理系统中得到拟建项目的单位造价。
通过模糊C均值聚类方法,借助MATLAB R1026a可以得出40个已完项目的聚类情况。设定聚类数目为3,3类中心坐标最大值个数分别为20、15、5,根据中心坐标值大的就是高造价,最小的就是低造价的原则,则第一类为高造价,第二类为中造价,第三类为低造价。其聚类结果如图1所示。
图1 已完高铁土建工程聚类结果
(二)模糊推理
模糊推理是一种基于人类直觉推理的方法,然后将其模糊化,从而可以对不确定的问题进行模糊化处理输出。其核心就是模糊推理的规则确定,即将专家以往的经验以一种语言概念的形式作为输入值,然后对其建立规则库和数据库,利用计算机的模糊推理功能得到输出值。
对于一阶Takagi-Sugeno模糊模型来说,其结构为3部分:第一,满足2条运算规则。
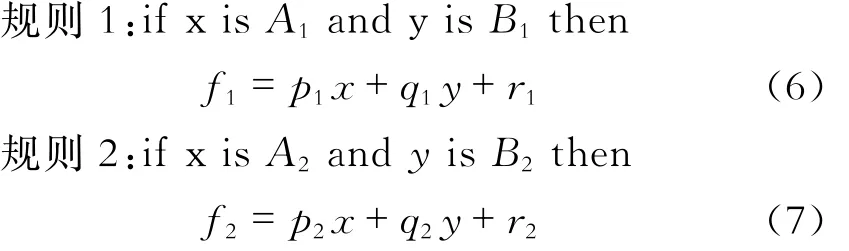
第二,数据库。又被称为知识库,是对指标的变化进行设定的隶属度函数,需要明确各个指标与输出数值的关系。
第三,推理机制。是系统内部的运算机理,它针对系统所要求的规则和搜集好的数据库执行推理的程序而产生一个合理的输出值。
其具体的运算机制如下所示。
第一层:将精确的变量进行“模糊化”描述。这一步骤需要在对系统进行输入之前确定,即确定不同指标的隶属度函数,若给定输入x,输出是该节点Ai的隶属度:

第二层:生成“如果—那么”式条件规则。表示输入到这一节点的信号的乘积,即:
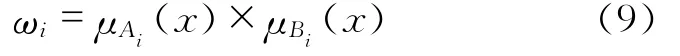
第三层:蕴涵层。每个节点都是圆节点,用N表示。这层的节点计算各个IF-THEN规则可信度与所有IF-THEN规则可信度之和的比值:

第四层:合成运算。每个节点都是方节点,节点响应函数定义为:ri),其中,pi,qi,ri为效应参数。即:

第五层:去模糊化。该层唯一的节点是用来表示的圆节点,用来计算所有输人信号的和。常用的去模糊化的方式有5种:粗糙集的面积重心(centroid)、模糊集的面积平分线(bisector)、模糊集最大隶属度对应的最小值(som)、最大隶属度对应的平均值(mom)、最大隶属度对应的最大值(lom)。文章主要采用粗糙集的面积重心(centroid),并且为离散性,其计算公式为:
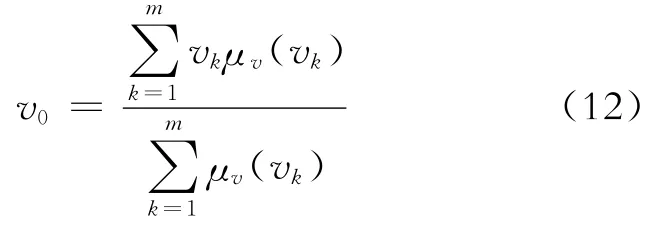
此模型的运算优点显著:①将隶属度函数和基础数据输入后,系统可以直接输出较为精确结果,通过结果数据确定需要的数值,便于分析;②相比较其他的预测方法,更加灵活、且计算方法较为简便高效;③运算机理将线性、非线性的计算方式组合到一起,结果可靠且便于后期结果的处理分析;④依靠计算机内部的计算机制,计算效率高。
(三)基于模糊C均值聚类推理的高铁土建工程造价智能估算模型构建过程
运用模糊C均值指标聚类算法,将已完工程聚类;同时,当拟建项目的已知工程特征数量不足显著性成本因子数量时,将已选好的显著性成本因子聚类,则得到新的影响拟建高铁项目工程造价的显著性成本因子。将因子和影响造价的模糊规则输入模糊推理系统。这些输入的数据既可以是数值形态也可以是模糊语言形态。最后,模糊推理系统计算实现对新建项目单位造价的投资估算。模糊推理的构建过程如下。
步骤一,将通过聚类得到的显著性成本因子作为输入因子,并且通过量化建立各个因子的隶属度函数。显著性成本因子体现拟建项目相对具体的工程特征。
步骤二,针对显著性成本因子建立模糊的推理规则,这基于显著性成本因子如何影响造价。模糊规则的建立也需要包括根据学界、业界的专家对拟建项目的显著性成本因子进行量化评分,作为系统输入的基础数据。
步骤三,将显著性成本因子作为输入函数,拟建项目的单位造价作为输出函数,建立整体的造价估算模型。输入显著性成本因子与单位造价之间的推理规则,进行新一轮的造价模糊推理运算,需要经过多次的实验选取最大程度上影响拟建项目造价变化的推理规则。经过系统自动计算后,系统会对拟建工程的造价进行“去模糊化”,则可得到所需的较为精确的工程造价预测数值,通过研究对象的特点对得出的预测数据进行界定为具体的造价值或比较系数。根据模糊C均值聚类方法确定的不同类别的已完工程造价数值和隶属度函数确定的输出值所处的区间,预测拟建项目的造价区间。
四、基于模糊C均值聚类推理模型的高铁土建工程造价智能估算分析
(一)工程概况
北仑—金塘海底高铁隧道是宁波—舟山铁路重要的一部分。宁波—舟山项目新建线路全长约为70.92 km,北仑—金塘是16.2 km的海底路段,其中海底盾构段长10.87 km,线路设计速度为250 km/h。这是国内首条海底高铁隧道。
(二)基于模糊C均值聚类显著性成本因子确定
在模糊C均值聚类推理的高铁土建工程造价智能估算模型的基础上,选取北仑—金塘海底高铁隧道为案例进行造价分析。由于该工程的已知工程特征数量远少于选取的显著性成本因子的数量,则将显著性成本因子进行聚类得到该项目的因子,连同影响其造价的模糊规则输入至模糊推理系统,得到其造价区间。本文设定需要的聚类数目为k类,最终经过反复试验确定k=3时,分类效果最为理想。首先确定将34个显著性成本因子用模糊C均值聚类算法,运用MATLAB R2016a后得到的聚类结果如图2所示。

图2 模糊C均值聚类结果
将聚类结果整合后,确定3类为:设备先进程度、环境条件、工程规模。
(三)基于模糊C均值聚类推理的高铁土建工程造价智能估算模型应用
1.构建模糊推理结构
通过初步构建模糊推理的思路,文章对其结构在MATLAB R2016a软件中进行表示为:类型:mamdani,交运算:min,并运算:max,去模糊化运算:Centriod,模糊推理:Min,合成运算:Max,输入:3个,即为已经确定好的3个显著性成本因子;输出:1个,即为该拟建项目与案例库中同类项目单位造价的比值;规则:6个,即为显著性因子在不同状态下的变化对单位造价的影响。其结构如图3所示。
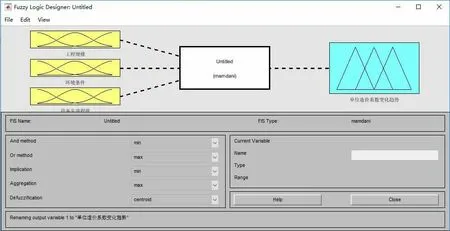
图3 模糊推理系统结构
2.确定各输入因素的数据库
各输入因素的数据库即隶属度函数,通过模糊C均值聚类获得的设备先进程度、工程规模、环境条件三个显著性因子及造价变化趋势的隶属度函数,分别如图4~图7所示。

图4 设备先进程度隶属函数
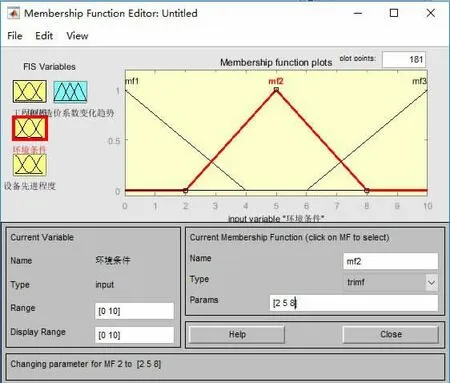
图5 工程规模隶属函数

图6 环境条件隶属函数

图7 单位造价系数变化趋势隶属函数
3.确定各输入因素的规则库
在建立了各因素的隶属函数后,需要确定规则库。需要选取其中最重要的部分输入至运算系统,从而在最大程度上决定造价的变化情况。确定的高速铁路土建工程显著性成本因子与单位造价存在以下逻辑推理关系:
若“设备先进程度”高且“环境条件”简单且“工程规模”小,则项目的单位造价低。
若“设备先进程度”高且“环境条件”复杂且“工程规模”小,则项目的单位造价中。
若“设备先进程度”中等且“环境条件”中等且“工程规模”中等,则项目的单位造价中。
若“设备先进程度”中等且“环境条件”复杂且“工程规模”大,则项目的单位造价高。
若“设备先进程度”低且“环境条件”复杂且“工程规模”大,则项目的单位造价高。
若“设备先进程度”低且“环境条件”简单且“工程规模”小,则项目的单位造价中。
以上规则在FIS Editor Viewer中如图8所示。

图8 模糊推理规则在FIS Editor Viewer中的表示
4.确定各输入因素的评分
根据项目的特征,分别对设备先进程度、环境条件、工程规模三个显著性成本因子通过学界、业界专家进行评分如表3所示。
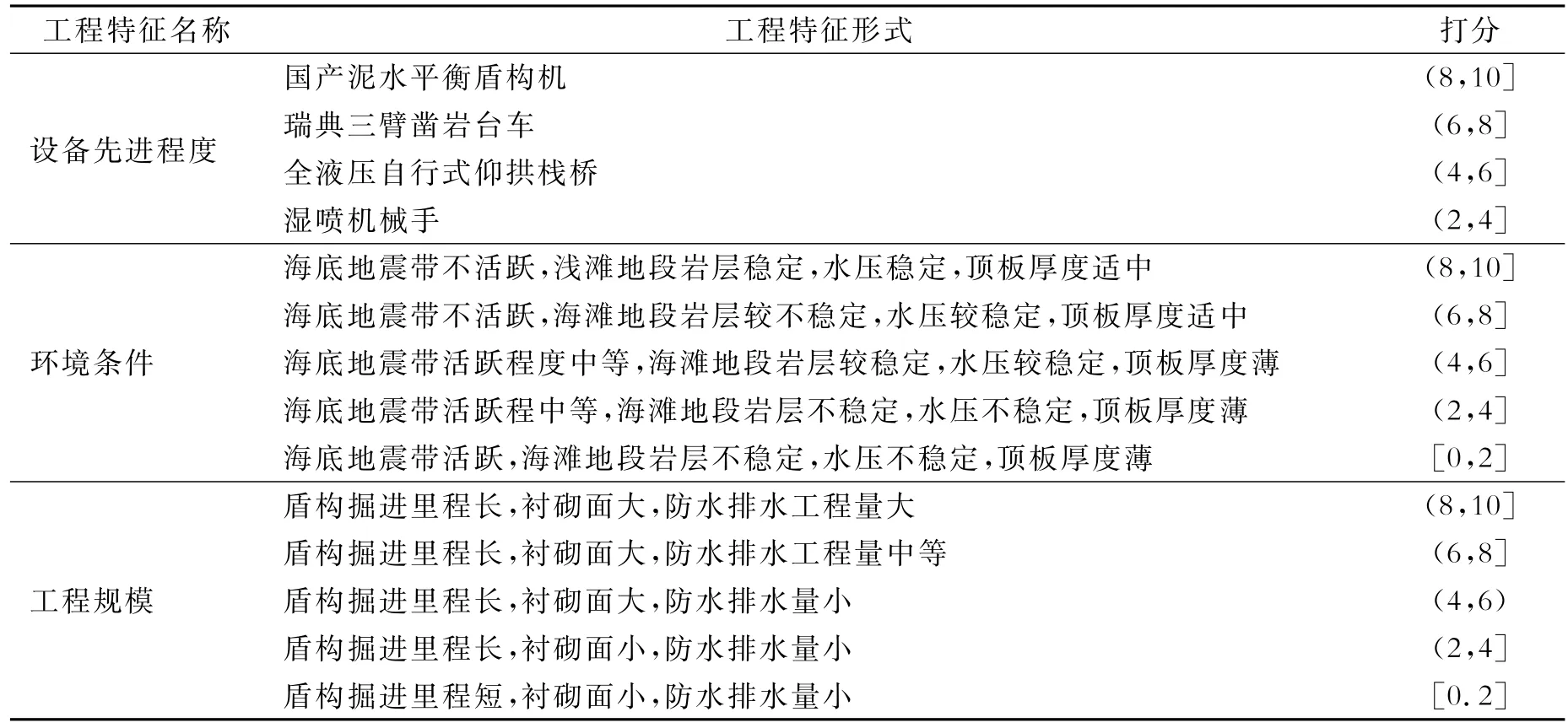
表3 显著性成本因子打分
经过对项目工程特征的分析及同已完工程的工程特征对比,得到针对北仑—金塘海底高铁隧道的显著性成本因子的得分为(8,7,9)。
5.造价预测值输出分析
将数据输入到MATLAB R2016a的模糊推理系统中,输出为5,结果如图9所示。
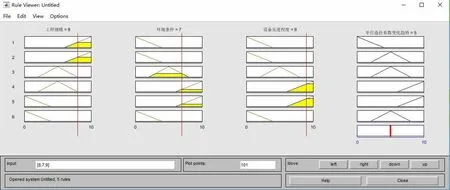
图9 北仑—金塘海底高铁隧道造价变化趋势
根据隶属度函数,该结果表示本项目为高造价,即为通过已完工程聚类的结果得知的高造价的项目单位造价的5倍。由上节通过模糊C均值项目聚类得出的高造价项目的造价值,可得出本项目的单位造价区间为[51 423.57,64 762.475](单位:万元),通过学术界和业界的论证,该项目的单位造价在此预测值范围内,因此用模糊C均值聚类推理的高铁土建工程造价智能估算方法来预测造价具有可行性。
五、结论
运用模糊C均值聚类算法与模糊推理相结合对高铁土建工程的造价进行智能预测,是一种非线性的投资估算方法,不同于以往简单、线性的造价估算。通过显著性成本理论确定显著性成本因子,可以提高估算的精度。将传统的数学计算方法同智能算法相结合可以降低造价工作的冗余性,提高工作效率,这对于减少投资估算的误差具有实际意义。

